Russian Federation
Vladivostok, Vladivostok, Russian Federation
Russian Federation
The article provides a review and analysis of mathematical models of the movement of a vessel, which is controlled by one or two rudder propellers, and the main tasks that are solved using these models. It has been pointed out that there are a sufficient number of mathematical models that describe the movement of a vessel equipped with a classical control scheme of propulsion: rudder - screw propeller. Such models are not applicable to the type of vessel under consideration. Since the ship is represented as a dynamic system with six degrees of freedom, which is affected by complex changing external conditions (wind, waves, etc.), then the ship’s control systems mainly use non-linear models, the construction of which, as well as their use is very difficult, due to their complexity and the small number of studies. To simplify the solution of problems related to the control of the vessel, it is promising to consider the movement of the vessel as plane-parallel. Thus, partial linearization of the model can be achieved by breaking the motion into two components: progressive and rotary motion, as well as using linear models for each part.
sea vessel, ship propulsion, azimuthing rudder propeller, vessel model, screw propeller, steering gear, propulsion and steering system
Введение
Задача управления морскими судами является актуальной и связана с необходимостью создания новых, современных систем управления, обеспечивающих безопасность мореплавания и энергосбережение. Даная задача неразрывно связана с использованием методов моделирования, для которых необходимо разработать математическую модель, учитывающую динамику судна при маневрировании в различных условиях плавания, а также с решением задач анализа и синтеза систем управления.
Для решения практически любой задачи синтеза систем управления математическая модель управляемого объекта является основой. Среди многообразия моделей динамики морских судов можно выделить классические модели линейного типа Номото 1-го и 2-го порядка, также нелинейные модели Норбинна и Беха [1, 2]. Но они описывают движение судна в контексте управления рулем, при этом скорость движения, боковой снос, влияние внешних воздействий не учитываются. Наряду с такими моделями используются модели плоскопараллельного движения (движения по поверхности) [3]. Как правило, эти модели представляются в векторно-матричной форме, являются многовходовыми (можно учесть несколько управляющих воздействий, внешние возмущения) и позволяют собрать вместе контролируемые величины (скорость поступательного движения, дрейф или боковой снос, рысканье).
Таким образом, использование многомерных моделей, представленных в векторно-матричной форме, является перспективным для описания движения судов, управляемых средствами активного управления.
Материалы исследования
Целью настоящего исследования являются вопросы управления при маневрировании судов, управляемыми винторулевыми колонками (ВРК), обзор моделей, используемых для представления динамики такого типа судов, и возможность параметрической идентификации для класса моделей, представленных в векторно-матричной форме.
При управлении движением судна различаются две основные задачи [1]:
– задача траекторного управления, состоящая в стабилизации движения по траектории запланированного маршрута, которая должна обеспечивать движение судна вдоль заданной траектории, минимизируя отклонение от нее;
– задача курсового управления, состоящая в удержании судна на заданном курсе.
В работах [4, 5] рассмотрены основные режимы управления для судов, оснащенных двумя азимутальными ВРК: круизный режим, или режим открытого моря, жесткий и мягкий режимы маневрирования, а также выполнение маневра остановки. В первом случае ВРК используются для маневров (операция швартовки и т. д). В этом случае происходит автоматическое снижение мощности примерно до 50–60 % самой системой (если такая возможность предусмотрена на судне), поворот на 360° разрешен. Во втором случае один ВРК, левый или правый (зависит от направления поворота), используется для выполнения маневров. При этом доступная мощность ограничена примерно 50–60 % от общей, а углы поворота ВРК ограничены 35°. Из-за того, что углы поворота ВРК δp ∈ [0; 360°], могут появиться нежелательные взаимные расположения ВРК, которые могут вызвать большой угол крена судна и поставить под угрозу его устойчивость, а также очень высокие нагрузки на конструкцию ВРК. При маневрировании во время остановки также должны соблюдаться ограничения на реверс оборотов гребного винта или разворот ВРК для создания обратной тяги (в этом маневре рекомендуется поворачивать ВРК наружу, но вращать их внутрь не запрещено).
В работе [6] обсуждаются основы управления судном с двумя поворотными ВРК азимутального типа. Рассмотрим и проанализируем приведенные результаты. Основное различие между управлением судном с обычным движительно-рулевым комплексом и судном, оснащенным ВРК, заключается в том, что поворот руля по правому борту заставляет судно поворачивать к правому борту, если рулевая колонка направлена по правому борту, то происходит поворот судна влево.
Более запутанная ситуация возникает, когда обе рулевые колонки (у судна, оснащенного двумя ВРК) используются одновременно и по отдельности. Без предварительной подготовки результат конкретной настройки ВРК достаточно трудно предсказать. Кроме того, возможность поворота ВРК на 360°, а также возможность изменения направления вращения гребных винтов приводит к тому, что многие другие маневры могут выполняться не так, как в обычных судах с движительно-рулевыми комплексами.
Движение судна с двумя ВРК (рис.) рассматривается как составное: поступательное движение или движение центра масс (точки G) (активное маневрирование при выполнении морских операций) и вращательное движение или вращение вокруг центра масс судна, расположенного на линии 0Х диаметральной плоскости (ДП) с координатами (0,5L; 0) (переход с одного постоянного курса на другой).
|
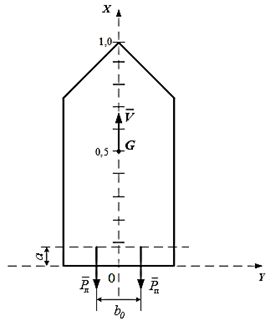
Поступательное движение судна
Для поступательного движения в работе [6] вводятся следующие допущения:
– рассмотрение движения судна как материальной точки G с действующим на нее суммарным вектором 
движущих сил и имеющей скорость, равную скорости поступательного движения судна V;
– постоянная скорость движения судна 
.
Основным конструктивным условием работы пропульсивного комплекса судов является симметричность работы движителей, т. е. 
.
Движение постоянным курсом требует устойчивости движения при определяющих параметрах: постоянной времени задержки и характеристики одерживания поворота. Упор винтов (см. рис., а) обеспечивает движение со скоростью 
силой , которая в условиях эксплуатации судна может быть определена по величине предельной мощности ВРК N (на швартовых) [6].
При появлении внешних возмущений их компенсацию предлагается производить двумя способами:
– незначительное уменьшение упора винта на борту, который противоположен стороне сноса;
– постоянная перекладка движителей на постоянный угол, при котором боковая сила компенсирует снос и манипулирование, для удержания на курсе, вокруг этого положения.
Выполнение перехода на новый курс
Выполнение перехода на новый курс при движении полным ходом можно выполнять двумя способами: синхронной перекладкой приводов обоих движителей на угол δр в сторону, противоположную повороту (см. рис., б), или сохранение одного из движителей неизменным и перекладка другого на определенный угол (см. рис., в).
Недостатком синхронного управления колонками для поворота является падение упора винтов, которое практически пропорционально углу перекладки колонки.
Другим способом экономичного удержания судна на курсе является выставление одной из колонок в положение параллельно ДП и манипулирование другой относительно среднего положения. Чтобы достигнуть максимального эффекта, манипулировать рекомендуется колонкой, которая находится на наветренном борту. Это незначительно уменьшает упор колонки и компенсирует снос, позволяя удерживать судно на курсе манипуляцией перекладки вокруг линии, параллельной ДП.
Если необходимо выполнить поворот на угол более 30°, то можно использовать перекладку колонки стороны поворота на угол до 90° (см. рис., в). Это соответствует результирующему упору на угол 45° (при симметричном упоре обоих винтов), однако при этом гидродинамическая сила на колонке будет уменьшаться за счет срыва потока воды.
Таким образом, выполнение операции удержания судна на курсе и поворот на полном ходу могут быть выполнены оптимальным образом при манипуляции одной из колонок. Однако получить расчетным способом значения сил на колонках затруднительно из-за отсутствия корректных методик определения гидродинамических сил на корпусе ВРК.
Математические модели движения судов
Математические модели движения судов, как и любые другие модели управляемых объектов, представляются в виде системы нелинейных дифференциальных уравнений, связывающих кинематические параметры движения судна с управляющими силами и моментами, формируемыми движительно-рулевым комплексом (ДРК), а также внешними силами, действующими на корпус судна в процессе движения. Как правило, подобные уравнения являются существенно нелинейными, и анализ их затруднен.
В классической литературе, как правило, приводятся модели морских судов, оснащенных традиционным ДРК типа «гребной винт – рулевое устройство»; моделей, описывающих движение судов, оснащенных винторулевыми колонками, – незначительное количество.
Анализ публикаций, материалов конференций показал, что интерес к подобному типу судов в последнее время вырос, но работ ограниченное количество.
В работах [4–12] описаны основы управления судном, оснащенным двумя ВРК. В работе [7] рассмотрена нелинейная модель с шестью степенями свободы, описывающими:
– поступательное движение:
где m – масса судна; 
, 
– проекции внешних сил на соответствующие оси координат; ωz – угловая скорость рыскания в системе горизонтальных осей тела; 
, 
– скорости продольного движения, бокового сноса; 
, 
, 
– ускорения продольного движения, бокового сноса и вертикальной качки; g – ускорение свободного падения.
– вращательное движение:
где Ixx, Iyy, и Izz – моменты инерции крена, дифферента и рыскания соответственно; θ – угол дифферента; 
, 
, 
– угловые скорости рыскания, крена, дифферента в системе горизонтальных осей тела; 
– внешние силы и моменты крена, дифферента и рыскания; 
– ускорение рыскания; 
– ускорение крена; 
– ускорение дифферента.
Модель разработана для описания движения пассажирского судна/парома (ROPAX), оснащенного азимутальной ВРК. Также в работе проведены сравнения между традиционной схемой управления «гребной винт – рулевое устройство» и управлением ВРК с использованием тестов маневрирования типа «зигзаг» с целью исследования устойчивости судна на траектории и курсе, а также влияния углов крена, вызванных влиянием ВРК при поворотах и движении судна при морском волнении.
Внешняя нагрузка, действующая на судно, в зависимости от схемы управления приведены в таблице 1.
Таблица 1 – Внешняя нагрузка, действующая на судно
|
Схема управления «руль – гребной винт» |
Схема управления с ВРК |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где индексы обозначают: 
– волновые силы и моменты; H – корпусные (маневренные) силы и моменты (в том числе силы сопротивления при поступательном движении), вызванные радиальными силами и моментами при вертикальных движениях; RD – силы и моменты руля; P – силы и моменты винта; POD – силы и моменты, вызванные приводами ВРК.
Приведенные результаты численного моделирования демонстрируют эффективность оптимизации конструкции судна с азимутальной ВРК для устранения любых проблем с устойчивостью и управлением, вызванных модификациями конструкции.
В работе [5] приведен сравнительный анализ процессов управления судами двух типов. Первый тип представлен судном, оснащенным традиционной движительной установкой, состоящей из толкающего одновинтового гребного винта и лопастного руля направления, вторая система основана на ВРК азимутального типа: тянущих или толкающих. Приведены уравнения, описывающие силы и моменты, возникающие в обеих системах. В работе [5] рассматривается упрощенная модель движения судна по трем координатам:
где 
, 
, 
– ускорения продольного и бокового поступательного движений, вращательного движения; 
– скорости продольного и бокового поступательного движений, вращательного движения; Xtot, Ytot – внешние силы продольного движения, бокового сноса; Iz – момент инерции рыскания; Ntot – внешние моменты рыскания; индексы обозначают соответственно: h – гидродинамические явления, связанные с движением корпуса судна в воде; asd – активные рулевые устройства, такие как главные движители или туннельные подруливающие устройства; psd – пассивные рулевые устройства, такие как руль направления; dis – внешние возмущения, такие как ветер, волны и т. д.
Также показаны примерные результаты моделирования для VLCC танкера «Blue Lady» в сравнении с экспериментами в реальном времени для двух типов судов.
В работах [9, 10] приведены математические модели танкера, оснащенного ВРК, которые представляют собой обобщенную систему нелинейных уравнений (3):
где V –скорость поступательного движения судна; 
– ускорение поступательного движения судна; FX, FY, Mz – силы тяги, продольная, поперечная, и вращательный момент; m11, m22, Jz66 – массоинерционные характеристики судна с учетом присоединенных масс λ11, λ22 (и инерций λ66 = 0); β –угол дрейфа;
– скорость изменения угла дрейфа; ω – угловая скорость поворота судна относительно вертикальной оси (рис. 1 б, в);
Как отмечают авторы [9], модель (3) менее исследована, но она может описывать движения судна, близкие к движениям лагом, например при выполнении швартовых операций. Это связано с тем, что в модели отсутствуют ограничения на угол дрейфа судна при работе ВРК в диапазоне углов 0–180° с каждого борта.
Другая математическая модель судна, управляемого двумя ВРК, представляет собой систему из 3-х дифференциальных уравнений, описывающих движения самого судна, и 2-х дополнительных уравнений вращения гребных винтов в водной среде:
где vy – поперечная линейная скорость поступательного движения судна; 
– относительная угловая скорость с учетом поступательного и вращательного движения в модели Тумашика; b1, b2 с2, с3, m1, m2, m3, m4 – коэффициенты, определяющиеся в зависимости от основных геометрических параметров погруженной части корпуса судна.
Приведенная система уравнений (4) дополнена уравнениями вращения гребных винтов в водной среде:
где 
– скорость вращения гребного винта; Mdv – момент, развиваемый электродвигателем ВРК; Mc – момент сопротивления винта в водной среде; Jv – момент инерции винта с учетом присоединенного момента инерции воды.
Момент двигателя Mdv рассчитывается как пропорциональный квадрату оборотов винта с регулирующей аддитивной добавкой, пропорциональной разности уставных (nUst) и фактических (ns) оборотов:
где 
, 
– поправочные коэффициенты.
В модели (3) не приводятся описания составляющих, входящих в продольную FX и поперечную FY силы, а также в выражения момента Mz. В модели (4) приведено описание входящих выражений для гидродинамических и аэродинамических составляющих. Остальные компоненты представлены в виде отдельных слагаемых, например FrX, FrY, Mr – усилия и момент на рулевом устройстве.
В работе [10] также подробно приводится методика расчета силовых составляющих, продольной, поперечной сил FrX, FrY и вращающего момента Mr для каждого ВРК.
Несмотря на то, что приведенные выше модели являются сложными ввиду своей существенной нелинейности, в работе [9] отмечается возможность параметрической идентификации моделей (3), (4) по результатам маневренных испытаний типа «Зигзаг 10/10».
Рассмотрим более простую модель плоскопараллельного движения судна, оснащенного двумя ВРК, приведенную в работах [11, 12]. Эта упрощенная модель судна описана в соответствии со стандартом IEC (International Electro-technical Commission) 62065. Стандарт IEC 62065 определяет минимальные эксплуатационные требования, требования к характеристикам, методы испытаний и требуемые результаты испытаний в соответствии со стандартами производительности для систем управления.
При синтезе модели (5) авторами [11, 12] предложен алгоритм преобразования математической модели движения суда с нестандартными движительно-рулевыми устройствами. В качестве примера для преобразования используется судно, оснащенное двумя ВРК и носовым подруливающим устройством (ПДУ). Настройка параметров модели в [11, 12] проводится по маневренным характеристикам (циркуляции), полученным при ходовых испытаниях.
Модель представляет систему дифференциальных уравнений:
где 
– продольная и поперечная скорости абсолютного движения (относительно земли); 
– продольное и поперечное ускорения абсолютного движения (относительно земли); 
– скоростные коэффициенты для продольного, поперечного и вращательного движений; 
, 
– нормированные значения тяги, формируемых ДРК и создаваемых морским волнением; r – угловая скорость рысканья; 
, 
– продольная и поперечная скорости относительного движения (относительно воды); 
– постоянные времени для продольного, поперечного и вращательного движений; – угловое ускорение рысканья; 
– нормированные значения моментов, формируемых ДРК и создаваемых морским волнением; γ – отношение расстояния центра давления боковых сил к длине судна (коэффициент стабильности).
Управление тягой:
где 
– скорость изменения тяги; P – значение мощности, потребляемое элементом управления; 
– скорость изменения мощности; Rp – скорость изменения мощности; индексы в обозначениях: a – текущее значение; d – заданные значения (уставка); для движительных комплексов: i = 1 – левая ВРК; 2 – правая ВРК; 3 – носовое подруливающее устройство
.
Управление рулевым (поворотным) устройством:
где δ – угол поворота ВРК; 
– скорость вращения ВРК; 
– скорость перекладки ВРК; 
– величина зоны нечувствительности.
Расчет текущего вращательного значения и его нормированного значения, приведенного в формуле (5), следующий:
где 
– нормированное значение момента, создаваемое ДРК; Mai – текущий момент, создаваемый i-м элементом управления; Mmax – максимальный вращательный момент, создаваемый ДРК; b – расстояние до ВРК от диаметральной плоскости; 
– текущее значение мощности, потребляемое i-ым элементом управления; 
– угол поворота ВРК, i=1,2...; 
– расстояние от ВРК до центра масс; 
– расстояние от носового ПУ до центра масс.
Модель движения судна, описанная уравнениями (5)–(8), по сравнению с моделями, описанными системами уравнений (3) и (4), является более простой для проведения параметрической идентификации с целью использования модели при проектировании системы управления движением судна.
Заключение
В работе выполнен анализ существующих моделей морских судов, оснащенных нестандартными движительно-рулевыми комплексами, а именно винторулевыми колонками. Как отмечено, традиционная модель, описывающая движение судна с классической схемой управления «руль – гребной винт», не применима к описанию динамики судов, оснащенных винторулевыми колонками, и, соответственно, использование классических моделей, таких как модель Номото и др., неприемлемо.
Существующие модели движения судов, оснащенных винторулевыми колонками, являются нелинейными в связи с отражением сложных гидродинамических взаимодействий рулевых устройств с внешней средой. В связи с этим перспективным является развитие методов параметрической идентификации моделей для использования их в задачах синтеза систем управления.
1. Os'kin D. A., Glazunov V. V., Vorob'eva S. A. Analiz matematicheskih modeley morskih sudov dlya zadach upravleniya dvizheniem // Nauch. problemy transporta Sibiri i Dal'nego Vostoka. 2010. № 1. S. 96-99.
2. Pomorski J., Morawski L., Rak A. Trajectory tracking control system for ship // IFAC Conference on Con-trol Applications in Marine Systems - CAMS'2004 (Ankona, Italy, July 7-9). 2004. V. 37 (10). P. 251-255.
3. Vaguschenko L. L., Cymbal N. N. Sistemy avtomaticheskogo upravleniya dvizheniem sudna: ucheb. Odessa: Feniks, 2007. 376 s.
4. Kobylinski L. Problems of Handling Ships Equipped with Azipod Propulsion Systems // Prace naukowe politechniki warszawskiej. 2013. V. 95. P. 232-245. URL: https://pdffox.com/problems-of-handling-ships-equipped-with-azipod-propulsion-systems-pdf-free-6492d89ae0bd4.html?utm_source=pingpdf (data obrascheniya: 18.07.2023).
5. Nowicki J. Stopping of Ships Equipped with Azi-pods // TransNav, the International Journal on Marine Navi-gation and Safety of Sea Transportation. 2014. V. 8. P. 373-376.
6. Golikov V. V. Metodologicheskie osnovy upravleniya sudnom s dvumya povorotnymi kolonkami Azipod // Sudovozhdenie: sb. nauch. rabot. Odessa: Vida-vInform, 2013. Vyp. 23. S. 56-64.
7. Ayaz Z., Turan O., Vassalos D. Manoeuvring and Seakeeping Aspects of Pod-Driven Ships // Proceedings of The Institution of Mechanical Engineers Part M-journal of Engineering for The Maritime Environment. 2005. V. 219. P. 77-91.
8. Gierusz W. Modelling the Dynamics of Ships with Different Propulsion Systems for Control Purpose // Polish Maritime Research. 2016. V.23. № 1(89). P. 31-36. URL: https://journal.mostwiedzy.pl/index.php/pmr/issue/view/48 (data obrascheniya: 18.07.2023).
9. Pashencev S. V. Sravnitel'nyy analiz matematicheskih modeley sudna s poziciy upravlyaemosti po otkloneniyam // Vestn. MGTU. 2017. T. 2, № 4. S. 673-680. URL: https://cyberleninka.ru/article/n/sravnitelnyy-analiz-matematicheskih-modeley-sudna-s-pozitsiy-upravlyaemosti-po-otkloneniyam (data obrascheniya: 15.05.2023).
10. Pashencev S. V., Egorov V. Yu. Analiz manevrirovaniya sudna, snabzhennogo dvumya azipodami, s pomosch'yu ego matematicheskoy modeli // Vestn. MGTU. 2019. T. 22, № 4. S. 461-470. URL: https://cyberleninka.ru/article/n/analiz-manevrirovaniya-sudna-snabzhennogo-dvumya-azipodami-s-pomoschyu-ego-matematicheskoy-modeli (data obrascheniya: 15.05.2023).
11. Glushkov S. V., Mazhirin I. A., Tyul'kanov A. K. Matematicheskaya model' dvizheniya sudov s nestandartnym dvizhitel'no-rulevym kompleksom // Vestn. MGTU. 2018. T. 21, № 4. S. 548-557.
12. Glushkov S. V., Mazhirin I. A. Uproschennaya matematicheskaya model' dvizheniya sudna s aktivnymi sredstvami upravleniya i ocenka ee adekvatnosti // Nauch.-tehn. sb. Ros. mor. registra sudohodstva. 2019. № 54-55. S. 39-48.
