Russian Federation
Astrahan', Astrakhan, Russian Federation
The article considers the problem of improving safety and efficiency of navigation of unmanned vessels. In the unmanned navigation, one of the most important tasks is planning a safe route, which consists in determining the shortest path in the shortest possible time and describing the motion of a marine vessel. The object of this study is the safe route of an unmanned vessel. There is given a review of the research literature on solving the problem of planning the route of sea and river mobile objects. The subject of the study is intelligent decision-making methods for safe route planning for unmanned navigation. The purpose of this article is to improve the safety of unmanned navigation by optimizing the route in the presence of one or more obstacles in the area of movement of an unmanned vessel that have a negative impact on the trajectory of movement. To achieve this goal, the task of local route planning was set and solved by the method of intelligent decision-making based on Biologically Inspired Neural Network (BINN). Methods of artificial intelligence and mathematical modeling were used to solve the problem. The results of the proposed method for solving the problem of planning a local route for an unmanned vessel confirm its ability of the vessel to avoid the local minima points. The simulation results show that the planned local route for unmanned navigation allows solving the problem of avoiding collisions with obstacles in real time, where the obstacles have only local effects. As part of further research, the described method is planned to be used for developing an information decision-making system for a movement control of an unmanned vessel.
planning, vessel’s route, unmanned navigation, neural networks, neural activity, unmanned vessel, safe zone
Введение
Одним из актуальных направлений современной прикладной науки является технология безэкипажного судовождения (БЭС), которая подразумевает развитие и внедрение на водных путях беспилотных морских судов, выполняющих автономное плавание по предварительно заданному маршруту и управляемых автономной бортовой системой. Технология БЭС развивается благодаря цифровым интеллектуальным технологиям, позволяющим повысить эффективность и безопасность управления беспилотными судами при изменяющихся внешних условиях. Для реализации плавания безэкипажных судов необходимо решать вопросы автономного предупреждения столкновения судов и интеллектуального планирования безопасного маршрута перехода [1–4].
В широком смысле задача планирования маршрута включает два аспекта: определение совокупности промежуточных путевых точек, через которые должно пройти безэкипажное судно с обходом возможных препятствий, и описание движения (геометрического пути) безэкипажного судна во времени [5].
Алгоритмы планирования маршрута можно классифицировать различными способами: по характеру внешней среды (глобальные и локальные), по точности (детерминированные и эвристические) [6].
Детерминированный подход, также известный как точный подход, представляет собой набор строго определенных шагов для создания уникального пути навигации, в то время как эвристический подход, широко принятый в качестве приближенного подхода, позволяет найти только приемлемое решение. Поэтому результат эвристического подхода не всегда обеспечивает наилучшее решение.
Глобальное планирование маршрута (global route planning) позволяет найти оптимальный путь от порта отправления к порту назначения при длительном плавании в условиях определенности (определенные географические характеристики окружающей среды, известная метеорологическая информация). Целью локального планирования маршрута (local route planning) судна является определение в режиме реального времени эффективного пути при наличиив области движения безэкипажного судна одного или нескольких препятствий, оказывающих негативное воздействие на траекторию движения [7, 8].
Состояние вопроса
Задача планирования маршрута рассмотрена во многих русско- и англоязычных статьях. Авторы работы [9] предложили систему динамического планирования траектории для недостаточно отработанных морских надводных транспортных средств на основе диаграммы Вороного, которая состоит из конечного множества различных точек P = {p1, p2, ..., pn} на плоскости, называемых генераторными точками. При обнаружении статического или динамического препятствия алгоритм переходит в фазу планирования и генерирует отклонение траектории на локальном уровне, что обеспечивает предотвращение столкновений с соблюдением Международных правил предупреждения столкновений судов в море, 1972 г. (МППСС-72).
В работе [10] предлагается использование метода нечеткой логики для интеграции нечеткой экспертной системы предупреждения столкновений судов на море и разработанной системы управления движением на основе H∞-оптимизации в пространстве состояний (автопилот H∞). Результаты моделирования показывают, что при применении предлагаемого в работе метода системы управления судном смогут заблаговременно определить подходящие воздействия по предотвращению столкновения, а также отслеживать желаемый путь в пределах допустимого диапазона до достижения места назначения.
Благодаря методу роя частиц (МРЦ) можно получить глобальный оптимальный путь и повысить безопасность движения судна. Методом роя частиц инициализируют группу случайных частиц (случайных решений), а затем находят оптимальное решение итерационным алгоритмом [6, 11]. Алгоритм работы МРЦ описывается следующей системой уравнений [12, 13]:
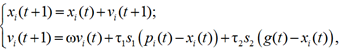
где xi(t), xi(t + 1) – позиция i-й частицы в моменты времени t и t + 1 соответственно; vi(t), vi(t + 1) – скорость i-й частицы в моменты времени t и t + 1 соответственно; ω – инерционный вес; τ1 = τ2 = 2 – константы; s1, s2 – случайные переменные на отрезке [0, 1]; pi(t) – лучшая позиция i-й частицы в момент t; g(t) – лучшая позиция в момент t для любой из частиц роя.
Авторы работы [14] предложили еще один алгоритм планирования траектории автономных судов на основе МРЦ с учетом влияния ветра и волн. Алгоритм никак не учитывает МППСС-72, но, в принципе, допускается к применению для конкретных условий плавания.
Также часто используется подход, основанный на методе искусственного потенциального поля, который позволяет построить гладкий путь и требует мало времени для расчета [6]. Однако, несмотря на наличие явных преимуществ, у метода искусственного потенциального поля существует ряд недостатков. Один из них – наличие локальных минимумов вследствие того, что силы притяжения и отталкивания находятся в противоположных направлениях в один момент. В случае достижения безэкипажным судном локального минимума в потенциальном поле алгоритм планирования пути может зацикливаться (это приводит к циклическому поведению судна). Вторым существенным недостатком является несоответствие между запланированным и реальным путем в навигационной практике.
Новый расширенный метод искусственного потенциального поля используется в работе [15]. Этот новый подход успешно решает проблемы планирования реактивного пути (например, сложный лабиринт с несколькими локальными минимумами), которые невозможно решить в рамках обычных статических потенциальных полей. Однако этот метод существенно более сложен для решения задачи автономного планирования маршрута судов и предотвращения столкновений в условиях динамической среды.
В работе [16] предложен алгоритм динамического окна с множеством математических моделей для генерации локальных траекторий движения. На основе критических факторов и правил МППСС-72 создана функция затрат для оценки навигационной безопасности (расчет риска каждой траектории), а не для определения оптимального локального маршрута. К использованию в глобальном планировании траектории для морского автономного надводного судна новый гибридный метод на основе методов скорости препятствий и марширующих квадратов впервые был предложен в работе [17]. Результатом в этом методе оказывается оптимальный кратчайший путь с учетом риска столкновения и расстояния между траекториями движения судна и препятствиями.
Важно отметить, что как локальные, так и глобальные алгоритмы планирования маршрута судов не обязательно должны быть отдельными. Некоторые алгоритмы (например, гибридный подход) выполняют задачу планирования в среде с препятствиями. Так, предлагаемый в работе [7] гибридный метод позволит планировать как глобальные (с помощью улучшенного метода искусственного потенциального поля), так и локальные (с помощью разработанного метода скорости препятствий) пути автономных судов. Но самый большой недостаток предлагаемого в работе [7] гибридного метода – вопрос точного отслеживания пути – не рассматривался, а также после определения локального пути не обсуждался вопрос о том, следует ли двигаться по первоначальному глобальному пути или продолжать движение по второму запланированному пути и как заставить судно двигаться по глобальному пути с целью безопасного перехода к порту назначения в условиях среды с вероятностными препятствиями.
В работе [8] описываются методы разбиения участка поверхности акватории вершинами графа, определения множества ребер графа и поиска кортежа вершин для определения кратчайшего пути на заданном графе в условиях штормовой погоды на основе реальных данных о параметрах морского волнения в водах Японского моря (правила МППСС-72 не учитываются).
Таким образом, к основным методам планирования маршрута судов относятся: диаграмма Вороного, методы нечеткой логики, метод роя частиц, метод искусственного потенциального поля, алгоритм динамического окна и др. Все вышеуказанные методы планирования маршрута судна имеют существенный недостаток: они применяются
в условиях определенности. Кроме того, система управления безэкипажным судном должна обеспечить способность принимать решения в режиме реального времени и адаптироваться к изменяющимся условиям окружающей среды, что является одним из преимуществ интеллектуальных методов принятия решений, которое заключается в постоянном взаимодействии с реальной окружающей средой [2, 3].
Метод и результаты исследования
При планировании маршрута безэкипажных судов в реальных условиях окружающей среды необходимо решить следующие задачи: моделирование комплексной внешней среды и планирование траектории в режиме реального времени с обходом препятствий или движущихся морских объектов.
В рамках этой целевой установки предлагается метод планирования локального маршрута на основе «вдохновленных биологией» нейронных сетей (Biologically Inspired Neural Network – BINN) для решения задач обеспечения безопасности движения безэкипажных судов в реальном времени. Главное свойство предлагаемого метода заключается в отсутствии традиционного состава нейронных сетей (входные, скрытые и выходные слои, а также функция активации). Ключевым моментом метода становится представление окружающей морской среды в виде взаимно однозначного соответствия между нейронами в нейронной сети.
Предположим, что движение безэкипажного судна осуществляется в декартовых координатах x, y c начальной точкой О (текущее место) к точке М (место назначения) (рис. 1).
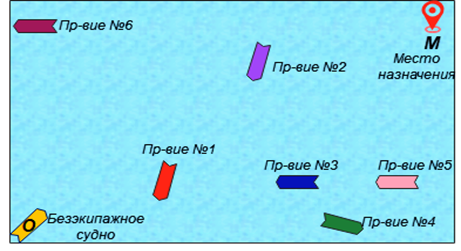
Рис. 1. Навигационная обстановка
в виде цифрового изображения
Fig. 1. Navigation environment as a digital image
На первом этапе BINN моделируется окружающая обстановка цифровым бинарным изображением в виде сетки местности, на которой препятствия оказываются темными участками изображения (квадратами), безопасные зоны плавания – светлыми. Затем представляем эту сетку в виде нейронной сети (рис. 2).
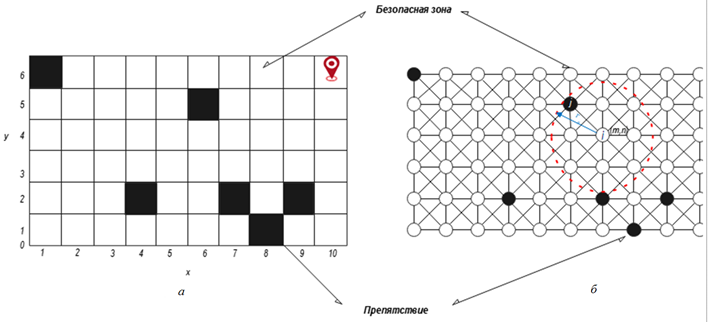
Рис. 2. Принципиальная схема нейронной сети: а – цифровая бинарная сетка местности;
б – представление сетки местности в виде нейронной сети
Fig. 2. Schematic diagram of the neural network: a – digital binary grid map;
б – representation of the grid map in the form of a neural network
На втором этапе BINN определяется ландшафт нейронной активности zi каждой ячейки в сетке следующим образом.
Динамика i-го нейрона в нейронной сети можно вычислить по формуле [18, 19]:
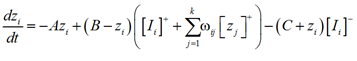 (1)
(1)
где zj – нейронная активность (мембранный потенциал) j-го соседнего нейрона; t – момент времени; A = 10 – скорость пассивного затухания нейронной активности; B = C = 1 – верхняя и нижняя границы нейронной активности соответственно; Ii – внешний вход i-го нейрона с координатами (m; n), который имеет следующий вид:

![]() – функция, возвращающая значение Ii, если Ii отрицательно (при наличии препятствия), и 0 в противном случае;
– функция, возвращающая значение Ii, если Ii отрицательно (при наличии препятствия), и 0 в противном случае; ![]() – функция, возвращающая значение Ii, если Ii положительно (при плавании безэкипажного судна в безопасной зоне), и 0 в противном случае; k – количество нейронных связей i-го нейрона с соседними нейронами; ωij – весовой коэффициент связи между i-м и j-м нейронами, который можно записать в виде
– функция, возвращающая значение Ii, если Ii положительно (при плавании безэкипажного судна в безопасной зоне), и 0 в противном случае; k – количество нейронных связей i-го нейрона с соседними нейронами; ωij – весовой коэффициент связи между i-м и j-м нейронами, который можно записать в виде
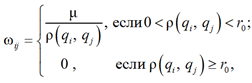
где µ = 0,7, r0 = 2 – положительные константы; ρ(qi,qj) – евклидово расстояние между центром ячеек (нейронов) i и j. При этом рецептивное поле ℜi для i-го нейрона представлено окружностью с радиусом r0. Таким образом, каждый нейрон имеет боковые связи только с 8 соседними нейронами в пределах своего рецептивного поля.
Нейронная сеть в этом случае состоит из 10 × 6 топологически организованных нейронов с нулевой начальной нейронной активностью. Решаем дифференциальное уравнение (1) в каждом нейроне и получаем следующую матрицу нейронной активности:

На рис. 3 показан ландшафт нейронной активности.
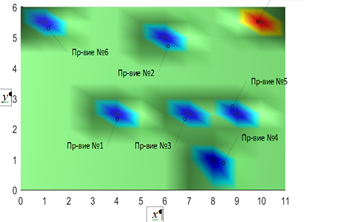
а
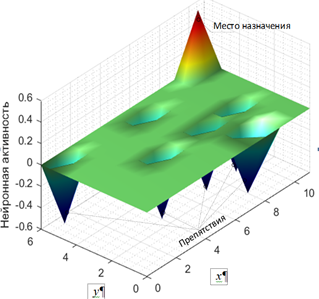
б
Рис. 3. Ландшафт нейронной активности:
а – двумерное компьютерное моделирование; б – трехмерное компьютерное моделирование
Fig. 3. The neural activity landscape:
а – two-dimensional computer modeling; б – three-dimensional computer modeling
На третьем этапе BINN генерируется локальный маршрут движения в реальном времени следующим образом.
Поскольку в формуле (1) имеются только возбуждающие нейронные связи, предлагаемая нейронная сеть гарантирует, что положительная нейронная активность может распространяться на все пространство сетки, но отрицательная активность остается только локальной. Таким образом, безопасные зоны глобально притягивают безэкипажное судно, в то время как опасные зоны препятствий действуют локально, отталкивая судно, чтобы избежать столкновения. Расположение безопасных зон и опасных зон на ландшафте может меняться со временем, например при наличии движущихся препятствий [20], поэтому ландшафт нейронной активности динамически изменяется
из-за изменяющихся внешних входных данных из изменяющейся окружающей среды и распространения внутренней активности между нейронами. На основе полученного ландшафта и предыдущих координат судна следующая точка (следующее местоположение) qt+1 на линии движения безэкипажного судна имеет вид
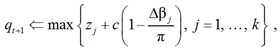
где zj – нейронная активность j-го соседнего нейрона; c – положительная константа; Δβj – угол поворота между текущим направлением движения судна и следующим направлением, т. е. если безэкипажное судно движется прямо, то Δβj = 0, если назад, то Δβj = π; k – общее количество соседних нейронов текущего нейрона, т. е. все возможные следующие местоположения судна. Таким образом, Δβj выражается как
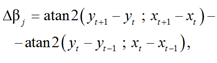
где (xt+1; yt+1), (xt; yt), (xt–1; yt–1) – декартовы координаты следующего, текущего, предыдущего местоположений соответственно; atan2(y; x) – функция, возвращающая арктангенс для заданных координат y и x :

Действительно, как показано на рис. 4, безэкипажное судно будет двигаться в направлении, где нейронная активность соседних нейронов больше, чем у текущего положения.
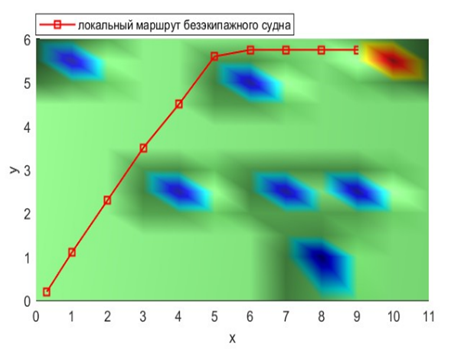
а
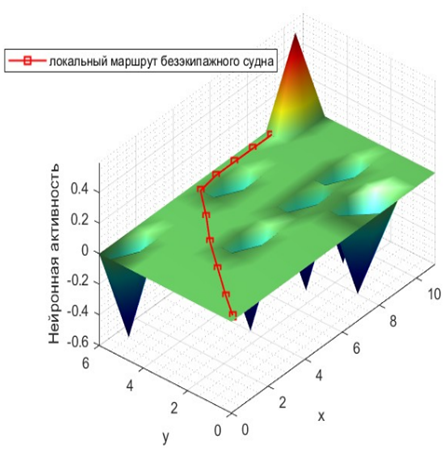
б
Рис. 4. Планируемый локальный маршрут при БЭС:
а – двумерное компьютерное моделирование; б – трехмерное компьютерное моделирование
Fig. 4. Planned local route at unmanned navigation:
а – two-dimensional computer modeling; б – three-dimensional computer modeling
А если нейронная активность не изменится в соседних нейронах, то судно будет двигаться вперед, т. е. судно должно проходить более короткий путь (с меньшим количеством препятствий) и делать меньше поворотов в направлении движения.
Заключение
Проблема поиска и планирования безопасного маршрута в задачах управления безэкипажными судами, исследуемая в работе, является актуальной. Проведен обзор наиболее распространенных методов планирования маршрута судна в среде с препятствиями. Предложен трехэтапный метод планирования локального маршрута на основе «вдохновленных биологией» нейронных сетей (BINN) на конкретном примере навигационной обстановки. Метод BINN открывает значительное количество возможных направлений будущих научных исследований в области беспилотных транспортных средств. Дальнейшая работа может быть направлена на разработку и использование
в задаче обеспечения безопасности при управлении БЭС гибридных подходов.
1. Barakat L. A., Kvyatkovskaya I. Yu. Predotvraschenie stolknoveniy pri bezekipazhnom sudovozhdenii na osnove algoritma glubokogo determinirovannogo gra-dienta strategii // Imitacionnoe i kompleksnoe modelirovanie morskoy tehniki i morskih transportnyh sistem: materialy VI Mezhdunar. nauch.-praktich. konf. (IKM MTMTS-2021) (Sankt-Peterburg, 23 iyunya 2021 g.). M.: Pero, 2021. S. 22-25.
2. Barakat L. Predotvraschenie stolknoveniy bezekipazhnyh sudov s ispol'zovaniem glubokogo obucheniya s podkrepleniem // Imitacionnoe i kompleksnoe modelirovanie morskoy tehniki i morskih transportnyh sistem (IKM MTMTS-2019): tr. V Mezhdunar. nauch.-praktich. konf. M.: Pero, 2019. S. 102-105.
3. Barakat L. A., Kvyatkovskaya I. Yu. Intellektual'noe prinyatie resheniy po avtonomnomu predotvrascheniyu stolknoveniy bezekipazhnyh sudov na osnove algoritma glubokoy Q-seti // 64-ya Mezhdunar. nauch. konf. Astrahan. gos. tehn. un-ta: materialy (Astrahan', 20-25 aprelya 2020 g.). Astrahan': Izd-vo AGTU. URL: http://www.astu.org/Content/Page/5833 (data obrascheniya: 19.03.2023) № gosudarstvennoy registracii 0322002778.
4. Barakat L. A. Markov decision-making process for autonomous collision avoidance of unmanned ships // X Regional Scientific and Practical Conference (Tomsk). Tomsk: Tomsk State University of Control Systems and Radioelectronics, 2021. P. 236-239.
5. Gasparetto A., Boscariol P., Lanzutti A., Vidoni R. Path Planning and Trajectory Planning Algorithms: A General Overview // Motion and Operation Planning of Robotic Systems. Mechanisms and Machine Science. 2015. V. 29. P. 3-27.
6. Lyu V. Metody planirovaniya puti v srede s prepyatstviyami (obzor) // Matematika i matematicheskoe modelirovanie. 2018. № 1. S. 15-58.
7. Zhang L., Mou J., Chen P., Li M. Path Planning for Autonomous Ships: A Hybrid Approach Based on Improved APF and Modified VO Methods // J. Mar. Sci. Eng. 2021. V. 9. P. 761.
8. Grinyak V. M., Grinyak T. M., Akmaykin D. A. Planirovanie marshruta perehoda morskogo sudna s uchetom parametrov volneniya // Territoriya novyh vozmozhnostey. Vestn. Vladivostok. gos. un-ta ekonomiki i servisa. 2018. № 4 (43). S. 99-111.
9. Candeloro M., Lekkas A. M., Sørensen A. J. A Voronoi-diagram-based dynamic path-planning system for underactuated marine vessels // Control Engineering Practice. 2017. V. 61. P. 41-54.
10. Hwang C. N., Yang J. M., Chiang C. Y. The design of fuzzy collision-avoidance expert system implemented by H∞-autopilot // Journal of Marine Science and Technology. 2001. V. 9, no. 1. Article 4. DOI:https://doi.org/10.51400/2709-6998.2432.
11. Han H. T., Ji W. F., Zhang Y. Q., Sha D. P. Comparative study of path planning by particle swarm optimization and genetic algorithm // Applied Mechanics and Materials. 2014. V. 687. P. 1420-1424.
12. Os'kin A. F., Os'kin D. A. Algoritm i programma chislennoy optimizacii, realizuyuschie metod roya chastic // Vestn. Polock. gos. un-ta. Ser. S. Fundamental'nye nauki. 2022. № 4. S. 26-31.
13. Rini D. P., Shamsuddin S. M., Yuhaniz S. S. Particle swarm optimization: technique, system and challenges // International journal of computer applications. 2011. V. 14, no. 1. P. 19-26.
14. Zhou Y., Gong Y., Geng X., Li D., Gao B., Li C. An Algorithm for Path Planning of Autonomous Ships Considering the Influence of Wind and Wave // Journal of Physics: Conference Series (2nd International Conference on Applied Physics and Computing (ICAPC 2021)). 2021. V. 2083. P. 032028. DOI:https://doi.org/10.1088/1742-6596/2083/3/032028.
15. Mabrouk M. H., McInnes C. R. Solving the potential field local minimum problem using internal agent states // Robotics and Autonomous Systems. 2008. V. 56, no. 12. P. 1050-1060.
16. Yang R., Xu J., Wang X., Zhou Q. Parallel trajecto-ry planning for shipborne Autonomous collision avoidance system // Applied Ocean Research. 2019. V. 91. P. 101875.
17. Chen P., Huang Y., Papadimitriou E., Mou J., van Gelder P. Global path planning for autonomous ship: A hybrid approach of Fast Marching Square and velocity obstacles methods // Ocean Engineering. 2020. V. 214. P. 107793.
18. Chen M., Zhu D. Multi-AV cooperative hunting control with improved Glasius bio-inspired neural network // The Journal of Navigation. 2019. V. 72 (3). P. 759-776.
19. Hodgkin A. L., Huxley A. F. A quantitative description of membrane current and its application to conduction band excitation in nerve // Bulletin of mathematical biology. 1990. V. 52, no. 1. P. 25-71.
20. Yang S. X., Luo C. A neural network approach to complete coverage path planning // IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics). 2004. V. 34 (1). P. 718-724.
















