Russian Federation
Russian Federation
The task is being solved to make a forecast of significant safety characteristics of aviation transport systems (ATS). A combined mathematical model based on the system dynamics apparatus and using regression analysis and graph theory has been developed. During the development of the model, significant ATS safety characteristics were selected, as well as frequent disturbances affecting the safety of operation were identified. A matrix of cause-and-effect relationships has been constructed, and a graph of relationships between model variables and perturbations has been developed. A system of nonlinear differential equations has been formed, the solution of which makes it possible to determine the magnitude of the main safety characteristics of the ATS operation under various environmental disturbances. The identification of regression coefficients and environmental equations is based on the analysis of data from open sources. The solution of a system of nonlinear differential equations is performed by the Runge–Kutta method of the 4th order of accuracy. The developed model is aimed at being used as part of decision support systems that model and predict the relevant characteristics of ATS systems that affect the safety of their operation. To demonstrate the capabilities of the model, computational experiments were conducted in which changes in the characteristics of the system over time were analyzed. To assess the accuracy of mathematical modeling of ATS security characteristics, model calculations were compared with data provided by security experts. The results obtained during the experiments confirm the adequacy of the developed model, which can be useful to managers and employees of flight safety management systems, as it will allow them to predict possible security threats at various time intervals and make adequate management decisions.
aviation safety, aviation transport system, system dynamics, forecasting, system modeling, operatio- nal safety
Введение
Распространенной причиной значительной части авиационных происшествий являются критические сочетания событий: отказы техники, неблагоприятные воздействия окружающей среды, ошибки экипажей, диспетчеров и др. [1].
Анализ причин этих происшествий показывает, что безопасность функционирования авиационных транспортных систем (АТС) достаточно полно характеризует такой показатель, как количество катастроф [2]. Данный показатель используется во многих официальных отчетах Межгосударственного авиационного комитета (МАК), динамика его изменения для стран, входящих в МАК, показана на рис. 1.
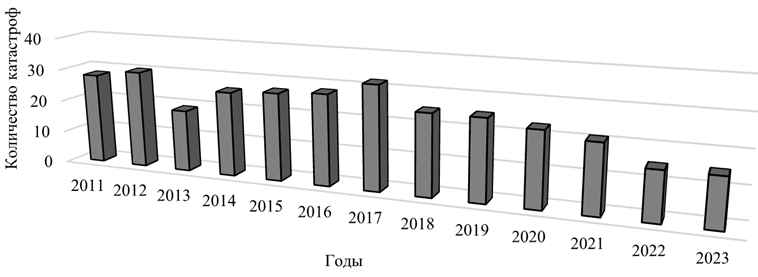
Рис. 1. Количество катастроф в авиации в странах МАК
Fig. 1. The number of aviation accidents in the IAC countries
Проблема снижения аварийности в процессе функционирования АТС рассматривалась в работах российских и зарубежных ученых, таких как Г. В. Новожилов, А. Ф. Резчиков, А. Д. Цвиркун, Н. В. Васильева, П. П. Новиков, А. В. Ефремов, М. С. Неймарк; M. B. Senol, C. M. Barroso, X. Yin, J. Guo, Y. Yuan и др.
Установление причин авиационных происшествий в работах Yu Changsheng производилось с использованием нечетких множеств [3], в трудах Jiuxia Guo для прогнозирования характеристики АТС использовался аппарат цепей Маркова [4]. В работах Mehmet Burak Senol для устранения аварийных ситуаций используется многокритериальное принятие решений [5]. В работе Chetan Chandra [6] анализировались отчеты о причинах авиационных происшествий путем распознавания именованных сущностей, что эффективно позволило найти самые распространенные причины авиационных происшествий. В работах Ibrahim Mohammad Alreshidi [7, 8] было предложено повысить безопасность функционирования АТС, анализируя электроэнцефалографические снимки мозга пилота во время пилотирования. В работах Afaq Khattak [9] анализировалась процедура пропущенного захода при посадке авиационного судна. У Zhuofu Yu [10, 11] анализировались размеры облаков в воздушном пространстве, в работе Qunyu Xu [12] изучалась активность птиц и ее влияние на безопасность авиации, в трудах Sandy Chkeir [13] производился прогноз и анализировалось влияние стихийных бедствий на воздушное движение. Изменение причин авиационных происшествий и катастроф было детально проанализировано в работе [14].
Перспективным направлением в изучении авиационной безопасности является применение искусственного интеллекта, в том числе нейронных сетей. В работе [15] нейронные сети используются для нахождения безопасных авиационных путей на карте при курсировании воздушного судна, что позволяет снизить число авиационных катастроф; нейронные сети используются для сравнения устойчивости авиационных материалов к урону [16]; в работе Chuen-Jyh Chen [17] используется сверточная нейронная сеть для прогнозирования видимости в условиях непогоды; Yiding Wang [18] тренирует и анализирует поведение нейросети, распознающей облака.
Другим важным направлением в сфере авиационной безопасности остается машинное обучение, в том числе глубокое обучение. В работе [19] машинное обучение используется для оценки ущерба авиационных катастроф. Сравнение моделей, прогнозирующих авиационные происшествие, по критерию точности было произведено в работе [20]. В [21] авиационные происшествия прогнозировались моделями машинного обучения с помощью метеорологических данных. Кроме того, для изучения массивов данных безопасности функционирования АТС применяется метод больших данных. В работе [22] собирались и анализировались данные о процессе функционирования АТС; в работе [23] был применен кластерный анализ для изучения данных об АТС; эффективно использовалась технология Big data для нахождения причин происшествий в [24]. Обзор патентов в сфере безопасности авиации приведен в [25]. Несмотря на большое количество применяемых методов, использованных для изучения проблемы аварийности АТС, в рассмотренных работах не были упомянуты математические модели, способные достаточно точно оценить и спрогнозировать основные показатели безопасности АТС под действием внешней среды. Таким образом, создание алгоритмов и математических моделей, способных определять характеристики безопасности АТС, является актуальным и экономически важным направлением исследований в сфере безопасности авиации. Прошли проверку практикой математические модели, основанные на аппарате системной динамики, позволяющие управлять процессом функционирования АТС или других систем [26–28].
Цель исследования – на основе системно-динамического подхода разработать математическую модель, позволяющую осуществить прогнозирование важных характеристик АТС на различных интервалах времени.
Разработка системно-динамической модели подразумевает решение следующих задач [29, 30]:
– выбор значимых переменных системы и внешних факторов, существенно влияющих на функционирование системы;
– формирование графа связей, наглядно показывающего взаимодействия между переменными модели и возмущениями окружающей среды;
– разработка системы нелинейных дифференциальных уравнений, решение которой позволит определить изменения выходных переменных модели на различных интервалах времени;
– проверка корректности модели (осуществляется по методике [2]).
Определение переменных системы
Анализ ежегодных отчетов МАК [31] позволил выбрать переменные системы АТС и внешние факторы, влияющие на безопасность функционирования АТС. Взаимосвязи между переменными модели и возмущениями окружающей среды характеризует граф связей (рис. 2): расшифровки принятых обозначений переменных модели и внешних возмущений приведены в табл. 1, 2.
Таблица 1
Table 1
Обозначения и названия переменных модели
Designations and names of model variables
|
Обозначение переменной |
Название переменной |
|
X1(t) |
Среднее время подготовки пилотов на сертифицированных тренажерах, дней в год |
|
X2(t) |
Среднее число авиационных катастроф на 100 тыс. ч налета в год |
|
X3(t) |
Повторяемость причин авиационных происшествий, % |
|
X4(t) |
Среднее количество нарушений инструкций пилотами на 100 тыс. ч налета в год |
|
X5(t) |
Доля устаревших воздушных судов свыше 15 лет, % |
|
X6(t) |
Показатель активности органов контроля за оборотом контрафакта, % |
|
X7(t) |
Доля частных судов в авиации, % |
|
X8(t) |
Количество сотрудников, задействованных в метеорологических службах |
Таблица 2
Table 2
Обозначения и названия внешних факторов модели
Designations and names of external factors of the model
|
Обозначение внешнего фактора |
Название внешнего фактора |
|
F1(t) |
Средняя по воздушным судам выработка ресурса до списания, % |
|
F2(t) |
Доля иностранных воздушных судов, % |
|
F3(t) |
Средний летный стаж пилотов, количество лет |
|
F4(t) |
Стоимость авиатоплива, руб. за т |
|
F5(t) |
Количество нормативно-правовых актов, относящихся к авиации |
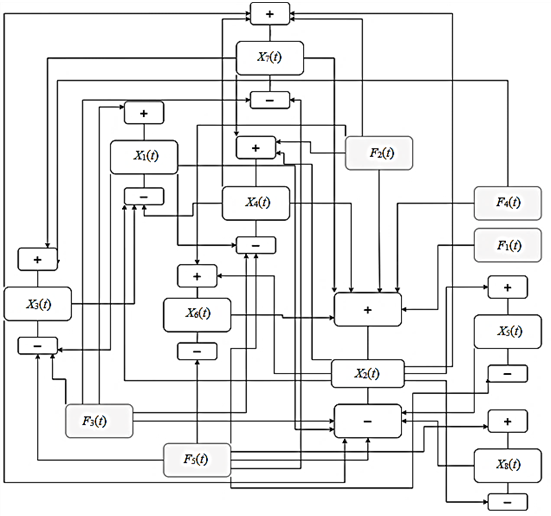
Рис. 2. Граф связей: «+» – наличие положительной связи; «–» – наличие отрицательной связи
Fig. 2. Graph of relationships: “+” – the presence of a positive connection; “–” – the presence of a negative connection
На рис. 2 взаимосвязи между переменными модели и внешними факторами построены на основе анализа мнений экспертов и анализа статистики [32]. Указанные зависимости представлены в виде матрицы связей (табл. 3): каждая клетка таблицы показывает, есть ли связь между соответствующими параметрами: «+» в таблице означает наличие положительной связи, т. е. при увеличении значений одной переменной увеличивается другая, а знак «–» – наличие отрицательной связи; если на пересечении строк и колонок таблицы отсутствует информация, то взаимосвязь между соответствующими переменными в модели отсутствует.
Таблица 3
Table 3
Связи между характеристиками и внешними факторами системы
Relationships between the characteristics and external factors of the system
|
Обозначение параметра |
X1(t) |
X2(t) |
X3(t) |
X4(t) |
X5(t) |
X6(t) |
X7(t) |
X8(t) |
F1(t) |
F2(t) |
F3(t) |
F4(t) |
F5(t) |
|
X1(t) |
|
– |
– |
– |
|
|
|
|
|
|
+ |
|
|
|
X2(t) |
– |
|
– |
+ |
+ |
+ |
+ |
– |
+ |
+ |
– |
+ |
– |
|
X3(t) |
– |
|
|
|
|
|
+ |
|
|
|
– |
+ |
– |
|
X4(t) |
– |
+ |
|
|
|
|
+ |
|
|
+ |
– |
|
– |
|
X5(t) |
|
+ |
|
|
|
|
|
|
|
|
|
|
– |
|
X6(t) |
|
+ |
|
|
|
|
|
|
|
+ |
|
|
– |
|
X7(t) |
|
+ |
+ |
+ |
|
|
|
|
|
+ |
– |
|
– |
|
X8(t) |
|
– |
|
|
|
|
|
|
|
|
|
|
+ |
В табл. 3 использованы данные отчетов МАК, собираемые ежегодно, а также данные из других открытых источников [2, 31, 32].
Составление системы дифференциальных уравнений модели
При помощи графа связей и таблицы связей между характеристиками и внешними факторами системы [29, 30] для каждой переменной модели составляются дифференциальные уравнения, имеющие следующий вид:
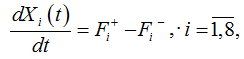
где ![]() – сумма внешних факторов модели, приводящих к возрастанию производной Xi(t);
– сумма внешних факторов модели, приводящих к возрастанию производной Xi(t); ![]() – произведение переменных модели, приводящих к возрастанию указанной производной;
– произведение переменных модели, приводящих к возрастанию указанной производной; ![]() – сложение внешних факторов модели, приводящих к убыванию указанной производной;
– сложение внешних факторов модели, приводящих к убыванию указанной производной; ![]() – произведение переменных модели, приводящих к убыванию указанной производной.
– произведение переменных модели, приводящих к убыванию указанной производной.
Таким образом, система дифференциальных уравнений модели может быть представлена в виде следующего выражения:
 (1)
(1)
С помощью графа связей и таблицы связей между характеристиками система (1) может быть записана в более развернутом виде:
 (2)
(2)
Функции fi(Xj(t)) характеризирует силу взаимосвязи между переменными модели, эти зависимости определяются, как правило, с помощью регрессионного анализа, а также с учетом мнения экспертов. Данные зависимости были определены в работе [32], с их учетом система (2) имеет вид
 (3)
(3)
Изменение внешних факторов имеет вид зависимостей, построенных на основе регрессионного анализа временных рядов для АТС [31]:
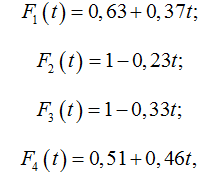
![]()
Для удобства анализа полученные результаты были пронормированы по соответствующему году, начальным моментом времени был выбран 2011 г.
Значения внешних факторов подставляются в систему уравнений (3). Итоговая система дифференциальных уравнений решается методом Рунге – Кутты 4-го порядка точности. На рис. 3 приводится график, который показывает количество катастроф с течением времени – X2(t) – в построенной модели.
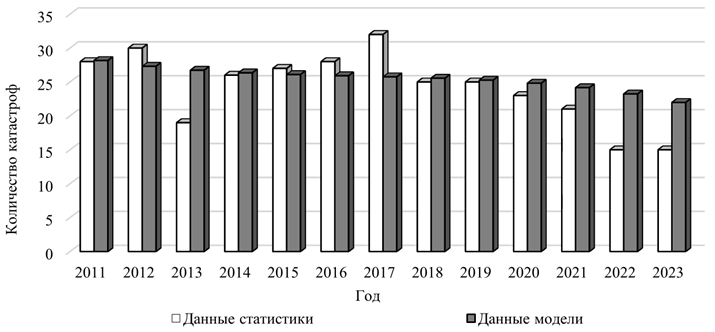
Рис. 3. Изменение количества катастроф на временном интервале 2011–2023 гг.
Fig. 3. Change in the number of disasters in the time interval 2011-2023
Проверка адекватности модели
Результаты расчетов подтверждаются данными статистики. На рис. 3 представлены сравнения расчетов и экспертных данных характеристики безопасности функционирования АТС, экспертные данные для характеристик были получены из анализа ежегодных отчетов МАК [31]. Предложенные отчеты показывают величины значимых характеристик безопасности функционирования за прошедшие годы. Таким образом, проверка корректности модели проводилась путем попарного сравнения за каждый год экспертных данных отчетов и результатов вычислений характеристик.
Модель, описывающая характеристики автоматизированных транспортных систем, хорошо соответствует реальным данным в большинстве случаев. Средневзвешенная процентная ошибка WAPE составляет 13,11 %.
Вычислительные эксперименты с моделью
С помощью полученной модели был выполнен ряд вычислительных экспериментов для определения того, как изменится количество катастроф при изменении других параметров модели.
Предположим, что количество нормативно-правовых актов в сфере авиации – контроль со стороны государства – было больше. На рис. 4 видно, что даже незначительное увеличение контроля со стороны государства F5(t) снижает количество катастроф X2(t) с течением времени.

Рис. 4. Снижение количества катастроф на временном интервале 2011–2023 гг.
Fig. 4. Reduction in the number of disasters in the time interval 2011-2023
Определить изменения системных параметров возможно не только при изменении значений внешних факторов, но и при изменении значений переменных системы. Например, увеличим коэффициент повторяемости авиационных происшествий в каждом году и проведем моделирование количества катастроф. На рис. 5 видно, что рост коэффициента повторяемости причин авиационных происшествий X3(t) приводит к росту количества катастроф X2(t).
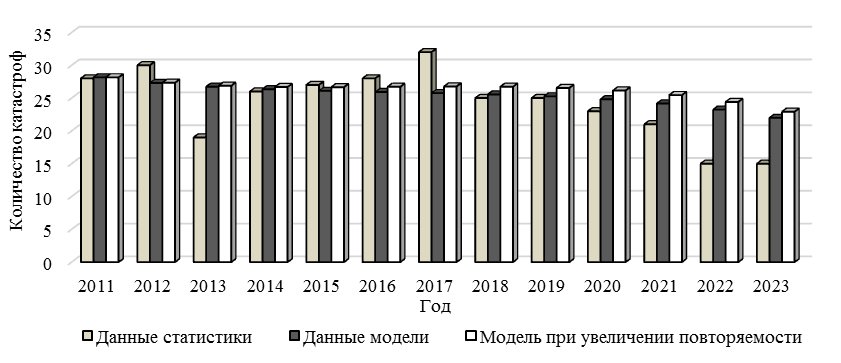
Рис. 5. Рост количества катастроф при увеличении коэффициента повторяющихся авиационных инцидентов
Fig. 5. An increase in the number of disasters with an increase in the number of recurring aviation incidents
Полученные результаты могут быть использованы лицами, принимающими решения в области обеспечения авиационной безопасности [33].
Заключение
Разработана математическая модель на основе системной динамики, позволяющая определить основные характеристики безопасности АТС из решений системы нелинейных дифференциальных уравнений. Разработано программное обеспечение, позволяющее решать систему уравнений с использованием различных численных методов, например Рунге – Кутты 4 порядка точности. Результаты моделирования могут применяться при обучении сотрудников и специалистов системы управления безопасностью полетов, а также при необходимости получить экспресс-оценку состояния характеристик безопасности авиационной транспортной системы.
1. Bogomolov A. S. Analiz putei vozniknoveniia i pre-dotvrashcheniia kriticheskikh sochetanii sobytii v chelove-komashinnykh sistemakh [Analysis of ways of occurrence and prevention of critical combinations of events in human-machine systems]. Izvestiia Saratovskogo universiteta. Novaia seriia. Seriia: Matematika. Mekhanika. Informatika, 2017, no. 12, pp. 219-230.
2. Kachur K. P., Rezchikov A. F., Kushnikov V. A., Bogomolov A. S., Filimonyuk L. Y., Ivaschenko V. A. Control of the air transportation system with flight safety as a criterion. Advances in Intelligent Systems and Computing, 2016, vol. 466, pp. 423-432.
3. Changsheng Y., Xubiao Y. Analysis of Safety Indicators Under the Framework of High-Quality Development of Civil Aviation. 2020 IEEE 2nd International Conference on Civil Aviation Safety and Information Technology. 2020. Pp. 1132-1137.
4. Guo J., Gao Z., Wang Y. Forecast of Civil Aviation Unsafe Events Rate Using Grey-Buffer Operator-Markov Chain Method. International Conference On Transportation and Development 2020: Transportation Safety. 2020. Pp. 71-82.
5. Şenol M. B. Evaluation and prioritization of technical and operational airworthiness factors for flight safety. Aircraft Engineering and Aerospace Technology, 2020, vol. 92, no. 7, pp. 1049-1061.
6. Chandra C., Ojima Y., Mavris D., Bendarkar M. Aviation-BERT-NER: Named Entity Recognition for Aviation Safety Reports. Aerospace, 2024, vol. 11, pp. 890-900.
7. Alreshidi I., Moulitsas I., Jenkins K. W. Multimodal approach for pilot mental state detection based on EEG. Sensors, 2023, vol. 23, no. 17, p. 7350.
8. Alreshidi I., Bisandu D., Moulitsas I. Illuminating the neural landscape of pilot mental states: a convolutional neural network approach with shapley additive explanations interpret-ability. Sensors, 2023, vol. 23, no. 22, p. 9052.
9. Khattak A., Chan P., Chen F., Peng H., Matara C. Missed approach, a safety-critical go-around procedure in aviation: prediction based on machine learning ensemble in learning. Advances in Meteorology, 2023, vol. 1, p. 1. DOI:https://doi.org/10.1155/2023/9119521.
10. Yu Z., Tan Z., Ma S., Yan W. Nowcast for cloud top height from Hi-mawari-8 data based on deep learning algorithms. Meteorology, 2023, vol. 30, no. 3, p. 2130.
11. Yu Q., Luo L., Liu B., Hu S. Re-planning of quadrotors under disturbance based on meta reinforcement learning. J. Intell. Robot. Syst. Theory, 2023, vol. 107, no. 1, p. 13.
12. Xu Q., Liu J., Su M., Chen W. Quantitative bird activity characterization and prediction using multivariable weather parameters and avian radar datasets. Aerospace, 2023, vol. 10, no. 5, p. 462.
13. Chkeir S., Anesiadou A., Mascitelli A., Biondi R. Nowcasting extreme rain and extreme wind speed with machine learning techniques applied to different input datasets. Atmos, 2023, vol. 282 (1), p. 106548. DOI:https://doi.org/10.1016/j.atmosres.2022.106548.
14. Mínguez C., Muñoz-Marrón D. Major air disasters: accident investigation as a tool for defining eras in commercial aviation safety culture. Aviation, 2023, vol. 27, no. 2, pp. 104-118.
15. Abin A. A. Using social media for flight path safety assessment. Aircraft Engineering and Aerospace Technology, 2021, vol. 93, no. 10, pp. 1664-1673.
16. Li A., Soltangharaei V., Bayat M., Van Tooren M. Detection of impact on aircraft composite structure using machine learning techniques. Measurement Science and Technology, 2021, vol. 32, no. 8, p. 084013.
17. Chen C. J., Huang C. N., Yang S. M. Aviation visibility forecasting by integrating Convolutional Neural Network and long short-term memory network. J. Intell. Fuzzy Syst., 2023, vol. 45, no. 3, pp. 5007-5020.
18. Wang Y., Gong J., Wu D., Ding L. Toward physics-informed neural networks for 3-D multilayer cloud mask reconstruction. IEEE Trans. Geosci. Remote Sens., 2023, vol. 61, no. 4, p. 741.
19. Omrani F., Etemadfard H., Shad R. Assessment of aviation accident datasets in severity prediction through machine learning. J. Air Transp. Manag., 2024, vol. 115. DOI:https://doi.org/10.1016/j.jairtraman.2023.102531.
20. Lamba M., Verma S., Kumar P. Generic Deep-learning-based time series models for aviation accident analysis and forecasting. SN Comput., 2024, vol. 5, no. 1, p. 32.
21. Caetano M. Aviation accident and incident forecasting combining occurrence investigation and meteorological data using machine learning. Aviation, 2023, vol. 27, no. 1, pp. 47-56.
22. Coelho e Silva L., Murça M. C. R. A data analytics framework for anomaly detection in flight operations. J. Air Transp. Manag., 2023, vol. 110, no. 10, p. 102409.
23. Clachar S. A. Identifying and analyzing atypical flights by using supervised and unsupervised approaches. Transp. Res., 2015, no. 2471, pp. 10-18.
24. Abedin M. A., Ng V., Khan L. Cause identification from aviation safety incident reports via weakly supervised semantic lexicon construction. J. Artif. Intell., 2010, vol. 38, pp. 569-631.
25. Yuan Y., Yu J., Zhang Y. Research on Technology Trend for Civil Aviation Safety based on Patent Big Data Analysis. 2020 IEEE 2nd International Con-ference on Civil Aviation Safety and Information Technology, 2020, pp. 987-991.
26. Spiridonov A. Yu., Rezchikov A. F., Kushnikov V. A., Bogomolov A. S., Ivashchenko V. A., Filimonyuk L. Yu. Prognozirovanie znachenii osnovnykh pokazatelei bezopasnosti funktsionirovaniia aviatsionnykh transportnykh sistem na osnove modeli sistemnoi dinamiki [Forecasting the values of the main safety indicators of aviation transport systems based on the system dynamics model]. Sistemy upravleniia i informatsionnye tekhnologii, 2017, vol. 68, no. 2, pp. 88-93.
27. Klyuev V. V., Rezchikov A. F., Kushnikov V. A., Bogomolov A. S., Ivashchenko V. A., Filimonyuk L. Yu., Khomutova M. V. Informatsionno-upravliaiushchaia sistema dlia podderzhki priniatiia reshenii po likvidatsii posledstvii navodnenii [Information management system to support decision-making on flood relief]. Vestnik komp'iuternykh i informatsionnykh tekhnologii, 2016, vol. 149, no. 11, pp. 39-45.
28. Iandybaeva N. V., Kozhanova E. R., Kushnikov V. A. Razrabotka programmnogo produkta dlia opredeleniia effektivnosti deiatel'nosti vysshego uchebnogo zavedeniia [Development of a software product for determining the effectiveness of higher education institutions]. Vestnik SGTU, 2014, no. 1, pp. 1–6.
29. Forrester J. W. World Dynamics. Allen Press Inc., 1973. 147 p. (Russ. ed.: Forrester D. Mirovaia dinamika / per. s angl. M.: OOO «Izd-vo AST», 2003. 379 s.).
30. Brodskii Iu. I. Raspredelennoe imitatsionnoe modelirovanie slozhnykh sistem [Distributed simulation of complex systems]. Moscow, Vychisl. tsentr im. A. A. Dorodnitsyna RAN, 2010. 156 p.
31. Otchety o sostoianii bezopasnosti poletov [Flight safety status reports]. Mezhgosudarstvennyi aviatsionnyi komitet. Available at: https://mak-iac.org/rassledovaniya/bezopasnost-poletov/ (accessed: 20.10.2024).
32. Spiridonov A. Y., Rezchikov A. F., Kushnikov V. A., Bogomolov A. S., Filimonyuk L. Y., Ivaschenko V. A., Dolinina O. N., Kushnikova E. V., Shulga T. E., Tverdokhlebov V. A., Kushnikov O. V., Fominykh D. S. Prediction of main factors values of air transportation system safety based on system dynamics. Journal of Physics: Conference Series. Conference Information Technologies in Business and Industry-2018. 2018. Pp. 32-40.
33. Rezchikov A. F., Tsvirkun A. D., Kushnikov V. A., Yandybayeva N. V., Ivashchenko V. A. Metody prognoznoi otsenki sotsial'no-ekonomicheskikh pokazatelei natsional'noi bezopasnosti [Methods of predictive assessment of socio-economic indicators of national security]. Problemy upravleniia, 2015, no. 5, pp. 37-44.















