Россия
Россия
Россия
Россия
На основе принципа максимума Понтрягина поставлены и решены две задачи оптимального управления нагревом жидкого продукта в нагревательной емкости жидким теплоносителем. В первой решается задача о быстродействии нагрева продукта до заданной температуры. Во второй задаче ищется управление, при котором осуществляется нагрев продукта за заданное время до заданной температуры при минимальном квадрате расхода теплоносителя. Приведены описание объекта управления со схемой потоков, система допущений, упрощающих составление модели, математическая модель объекта управления, постановки задач оптимального управления и полученные решения. В задаче о быстродействии нагрева получены аналитические выражения для определения температуры продукта, теплоносителя и времени управления. Приведен пример решения задачи о быстродействии нагрева с иллюстрацией динамических характеристик переменных объекта и найденного оптимального управления. При оптимальном процессе расход теплоносителя в любой момент времени равен одному из двух своих предельных значений. Оптимальный процесс состоит не более чем из двух интервалов. В задаче о минимизации квадрата расхода теплоносителя решение получено численным способом. Задача нахождения оптимальных траекторий переменных и управления сформулирована как краевая задача с недостающими начальными условиями, поиск которых реализован с помощью разностного метода решения краевой задачи. На основе найденных начальных условий решена задача Коши расширенной системы уравнений, получена оптимальная траектория изменения температуры продукта и расхода теплоносителя. Приведен пример решения задачи о минимизации квадрата расхода теплоносителя с демонстрацией динамических характеристик переменных объекта и найденного оптимального управления.
оптимальное управление, оптимальное управление нагревом, принцип максимума Понтрягина, вариационное исчисление
Введение
На предприятиях пищевой, химической и нефтехимической промышленности часто встречается задача нагрева или охлаждения жидкого сырья или продуктов переработки в емкостях, оснащенных «рубашками» с циркулирующим в них теплоносителем или хладагентом [1–3]. В больших емкостях как для нагрева, так и для охлаждения содержимого до нужной температуры требуются значительные энергетические затраты, поэтому управление тепловыми процессами часто является определяющим фактором в технико-экономических показателях производства.
Математическое описание объекта исследования
Рассмотрим емкость с мешалкой, оснащенную снаружи рубашкой, в которую непрерывно подается жидкий теплоноситель (рис. 1).
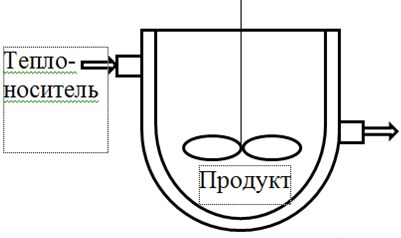
Рис. 1. Схема потоков в емкости с рубашкой
Fig. 1. Flow diagram in a tank with a jacket
Нагрев продукта до заданной температуры осуществляется после полной загрузки продукта в емкость, конвективные потоки продукта на входе и выходе емкости в процессе нагрева отсутствуют. Передача тепла от теплоносителя продукту осуществляется через разделяющую емкость и рубашку поверхность. В рассматриваемой емкости установлено перемешивающее устройство, поэтому можно принять допущение, что в емкости отсутствует передача тепла теплопроводностью. Поскольку в рубашку непрерывно подается теплоноситель, имеются конвективные потоки теплоносителя на входе и выходе рубашки. Как и для емкости, примем допущение о том, что передача тепла в рубашке за счет теплопроводности незначительна. Будем полагать, что нет теплообмена между теплоносителем и окружающей средой через поверхность рубашки.
С учетом принятых допущений емкость и рубашку емкости можно описать моделью для аппарата идеального смешения [4] (периодического для емкости и непрерывного – для рубашки).
Уравнения скорости изменения температуры в емкости T1 и рубашке T2 в виде уравнений Коши будут выглядеть следующим образом:
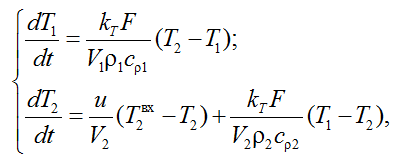(1)
где kT - коэффициент теплопередачи, кДж/(м2·ºС·с); F – площадь поверхности теплообмена, м2; V1 и V2 - объемы емкости и рубашки соответственно, м3;
ρ1 и ρ2 - плотности продукта и теплоносителя, кг/м3; cρ1 и cρ2 – удельные теплоемкости продукта и теплоносителя, кДж/(кг·ºС); u – объемный расход теплоносителя в рубашку, м3/с; 
– температура теплоносителя на входе в рубашку, ºС.
Для дальнейшего удобства представим систему уравнений (1) в следующем виде:
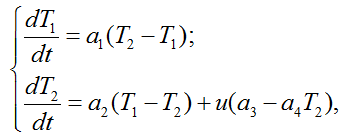(2)
где 
.
Зададим граничные условия для обеих переменных в начальный tн = 0 и конечный tк = Т моменты времени:
(3)
Управляющим воздействием в задаче нагрева жидкого продукта в емкости с рубашкой является расход теплоносителя, подаваемого в рубашку.
Задача о быстродействии нагрева
Функционал качества управления в задаче о быстродействии задается в виде
(4)
Укажем ограничение, налагаемое на расход теплоносителя в рубашку емкости
где Umax – максимально допустимый расход теплоносителя.
Требуется определить такой расход теплоносителя в рубашку u*(t), который обеспечивает перевод объекта в заданное состояние за минимальное время.
Уравнения системы (2) являются линейными, поэтому принцип максимума Понтрягина будет и необходимым, и достаточным условием оптимальности для решения поставленной задачи [5].
Составим гамильтониан для заданной задачи:
(5)
где 
– сопряженные функции к системе уравнений (2) и подынтегральному выражению
в функционале (4).
Рассматривая в гамильтониане только член, зависящий от искомого управления u(t) и сопряженных функций, получим из выражения (5)
.
Чтобы гамильтониан (5) принимал максимальное значение, необходимо всякий раз, когда ψ2(a3 – a4T2) > 0, соблюсти управление u(t) = Umax, и u(t) = 0 в случае, когда ψ2(a3 – a4T2) ≤ 0. Поскольку разница a3 – a4T2 всегда больше или равна нулю (в данной задаче температура теплоносителя в рубашке не может быть больше температуры теплоносителя на входе в рубашку), максимум гамильтониана H(T, ψ, u) определяется знаком функции ψ2:
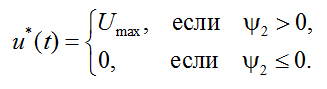(6)
Закон управления (6) справедлив на всем интервале управления 
.
Для нахождения оптимального управления, в том числе количество переключений управления между u(t) = 0 и u(t) = Umax, необходимо определить выражение для сопряженной функции ψ2(t), при которой система уравнений (2) удовлетворяет граничным условиям (3).
Сопряженные переменные определяются уравнениями
,
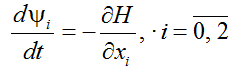и выглядят следующим образом:
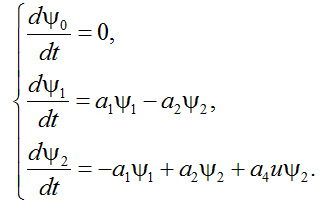(7)
Общее решение системы уравнений (7) имеет вид
(8)
где
,
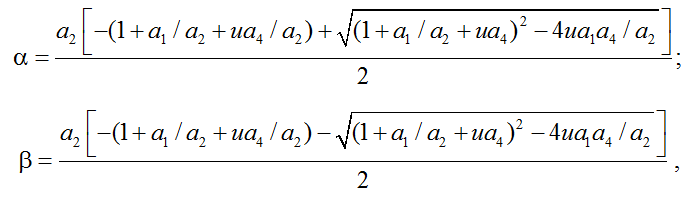а S0, S1, S2 – постоянные интегрирования системы (7).
Из выражения (8) видно, что функция ψ2(t) при любых значениях S1 и S2 не более одного раза меняет знак на отрезке времени t. Это означает, что управление u(t) состоит из не более двух интервалов управления с u(t) = 0 и u(t) = Umax.
Обыкновенно постоянные интегрирования в решении дифференциальных уравнений определяются из начальных условий, но начальные условия для сопряженных функций неизвестны. Неизвестны они и для конечных условий. Их роль выполняют начальные и конечные условия для температур, поэтому постоянные интегрирования для сопряженных функций найдем после определения
T – времени функционирования объекта под воздействием управления u(t), а для этого проинтегрируем уравнения системы (2).
Очевидно, что в начальный момент времени при t = 0 объект функционирует под воздействием управления u(t) = Umax.
Общее решение системы уравнений (2) с управляющим воздействием u(t) = Umax выглядит следующим образом:
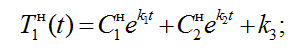(9)
(10)
где 
– функции температуры в емкости и рубашке в начальный момент времени; 
– постоянные интегрирования системы (2) для начального момента времени, а значения k1–k3 в выражениях (9) и (10) находятся как
.
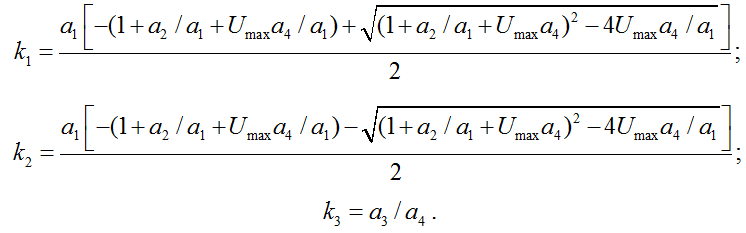Используя начальные условия при t = 0, определяем постоянные интегрирования:
.
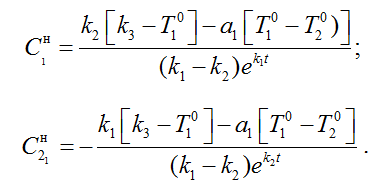В конечный момент времени t = T объект функционирует под воздействием управления u(t) = 0,
а общее решение системы уравнений (2) имеет вид
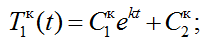(11)
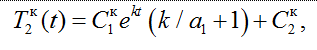(12)
где 
– функции температуры в емкости и рубашке в конечный момент времени t = T; 
– постоянные интегрирования системы (2) для конечного момента времени, а значение k в выражениях (11) и (12) находится как k = –a1(1 + a2/a1).
Используя условия на конец управления при t = T, определяем постоянные интегрирования:
.
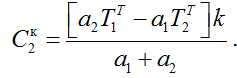Время управления T и время смены управляющего воздействия τ находятся из условия неразрывности решения в момент времени τ:
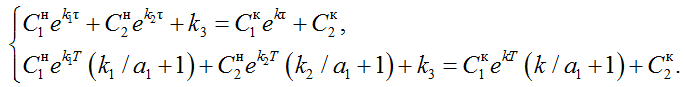(13)
Руководствуясь условием теоремы принципа максимума, согласно которому на интервале управления 
выполняется тождество 
из уравнений гамильтониана в начальный и конечный моменты времени, находим постоянные интегрирования S1, S2 и искомое выражение для сопряженной функции 
.
Приведем пример решения.
В таблице приведены конструктивные и теплофизические параметры для исследуемого объекта.
Параметры объекта управления
Parameters of the control object
|
Параметр |
Значение |
|
Объем емкости V1, м3 |
10 |
|
Объем рубашки V2, м3 |
3 |
|
Поверхность теплообмена F, м2 |
30 |
|
Коэффициент теплопередачи kT, кДж/(м2·ºС·с) |
1,1 |
|
Плотность продукта ρ1, кг/м3 |
906 |
|
Плотность греющей воды ρ2, кг/м3 |
960 |
|
Удельная теплоемкость продукта cp1, кДж/(кг·ºС) |
1,7 |
|
Удельная теплоемкость греющей воды cp2, кДж/(кг·ºС) |
4,2 |
|
Температура греющей воды на входе в рубашку T2вх, ºС |
95 |
|
Допустимые границы изменения расхода греющей воды в рубашку, м3/c |
|
Граничные условия для переменных в начальный tн = 0 и конечный tк = T моменты времени:
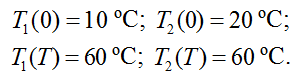
В начальный момент времени при tн = 0 под воздействием управления u(t) = Umax в соответствии с (9), (10) объект описывается уравнениями
,
а в конечный момент времени при tк = T, при u(T) = 0 решение системы уравнений (2), в соответствии с (11), (12), имеет вид
.
Из уравнений неразрывности (13)
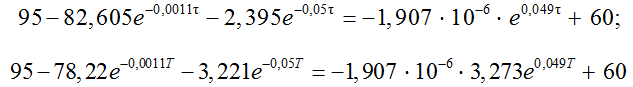
находим время переключения управляющего воздействия и период управления. Время смены управляющего воздействия составило τ = 749 с, время управления T = 777 с.
Постоянные интегрирования сопряженных функций ψ1(t) и ψ2(t) найдены из уравнений равенства гамильтониана нулю в начальный и конечный моменты времени. Выражения для сопряженных
функций ψ1(t) и ψ2(t) выглядят следующим образом:
.
Результаты решения задачи оптимального нагрева продукта в емкости приведены на рис. 2 и 3.
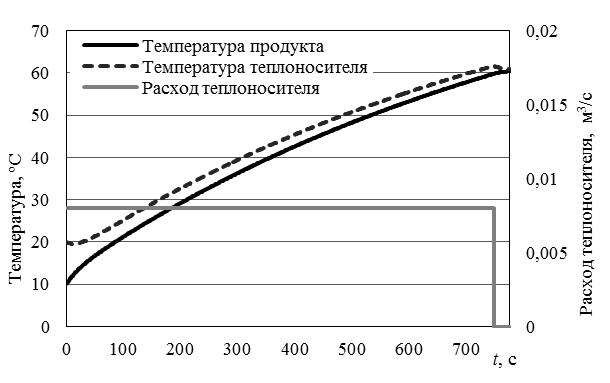
Рис. 2. Графики температур и оптимального управления
Fig. 2. Graphs of temperatures and optimal control
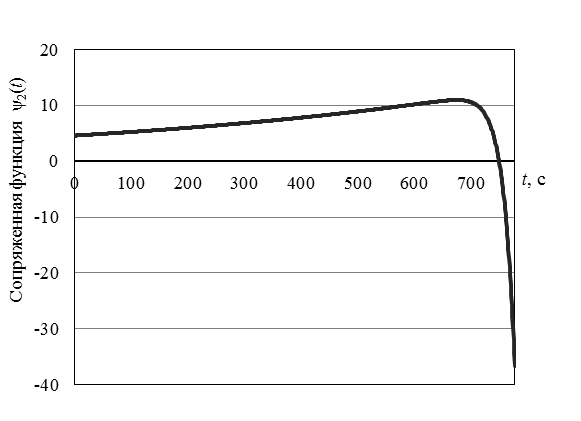
Рис. 3. График сопряженной функции 
Fig. 3. Graph of the conjugate function 
Из анализа графика на рис. 2 следует, что управление носит кусочно-непрерывный характер. Управляющее воздействие u(t) достигает только своих предельных значений. Момент переключения управляющего воздействия u(t) на рис. 2 совпадает с моментом времени перехода функции ψ2(t) через нуль на рис. 3. Наименьшее время перевода объекта из начального в конечное состояние составило 777 с. Объем затраченного теплоносителя составил 5,99 м3.
Задача о минимизации квадрата расхода теплоносителя
Функционал качества управления в задаче о минимизации квадрата расхода теплоносителя зададим в виде
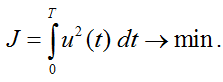(14)
Заданы начальные условия для обеих переменных в начальный tн = 0 момент времени
и значение переменной T1 в конечный момент времени tк = T
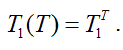
Остается ограничение на расход теплоносителя в рубашку емкости
Требуется определить такой расход теплоносителя u*(t), который обеспечивает нагрев продукта
в емкости до заданной температуры за фиксированное время T, при этом функционал (14) достигает минимального значения.
Гамильтониан для заданной задачи имеет вид
.
Найдем частную производную гамильтониана по управлению u и из равенства нулю этой производной определим выражение для управления как функцию времени
.
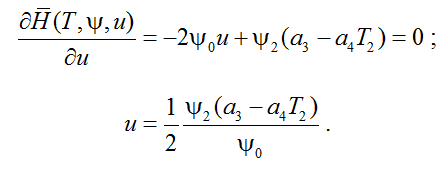Принимая во внимание, что число ψ0, согласно принципу максимума, равно –1, получим
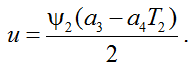(15)
В соответствии с (15) оптимальное управление примет вид
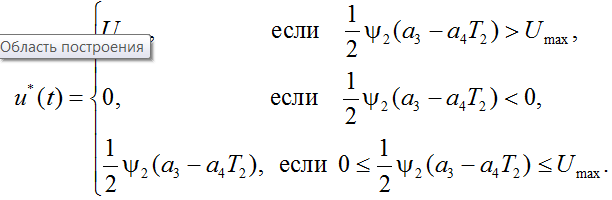
Составим расширенную систему уравнений с найденным для u выражением (15):
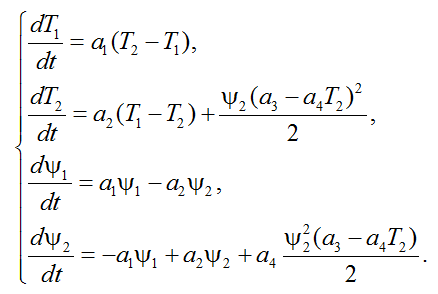(16)
Полученная система (16) является системой нелинейных обыкновенных дифференциальных уравнений, решение которой возможно только численно. Но решить ее, как задачу Коши, невозможно, т. к. отсутствуют начальные условия для сопряженных переменных. А поскольку задано граничное условие для температуры продукта в конечный момент времени, а второе граничное условие вытекает из условия трансверсальности для задач с нефиксированными концами [5], согласно которому ψ2(T) = 0, задача (16) становится краевой.
Наиболее популярный метод решения краевой задачи – метод стрельбы [6], заключающийся в последовательном подборе недостающих начальных условий на левой границе расчетного интервала и решении затем полученной задачи Коши до приведения к заданным граничным условиям на правой границе интервала, – оказался непригоден в вычислительном плане и не позволил найти начальные условия для сопряженных переменных.
Решение краевой задачи было получено с помощью разностного метода [7]. Для этого временной расчетный интервал был покрыт сеткой из ЬN точек с N – 1 шагами решения. Дифференциальные уравнения системы (16) были заменены их разностными аналогами:
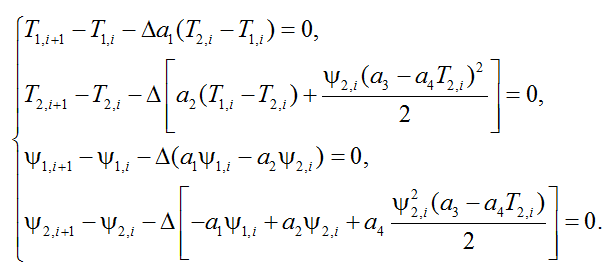(17)
Полная система нелинейных алгебраических уравнений для N – 1 шагов сетки состоит из N – 1 систем (17) с неизвестными T1,i и T2,i (
),
и четырьмя граничными условиями:
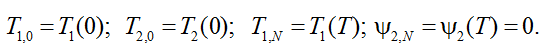
Система имеет единственное решение, которое найдено с помощью численного метода Ньютона – Рафсона. В результате решения были получены недостающие начальные условия для сопряженных переменных. Так, для емкости из примера, данные которой представлены ранее в таблице, начальные приближения сопряженных переменных составили 
.
На рис. 4 показаны графики изменения температуры продукта и теплоносителя, а на рис. 5 график изменения расхода теплоносителя на одном из участков горизонта управления для времени управления равного 1 800 с.
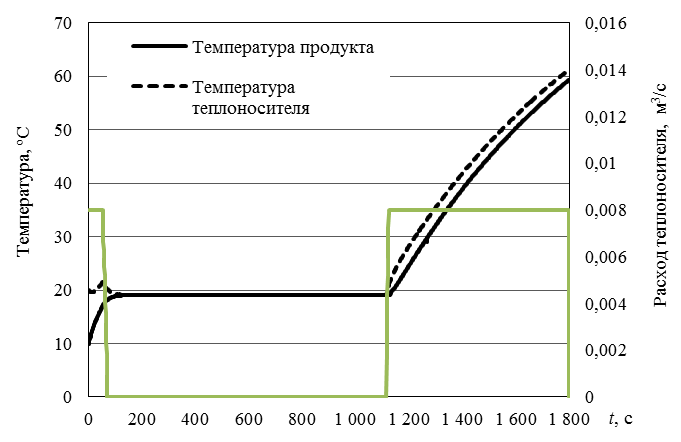
Рис. 4. Графики температур и оптимального управления в задаче минимизации квадрата расхода теплоносителя
Fig. 4. Graphs of temperatures and optimal control in the task of minimizing the square of the coolant flow
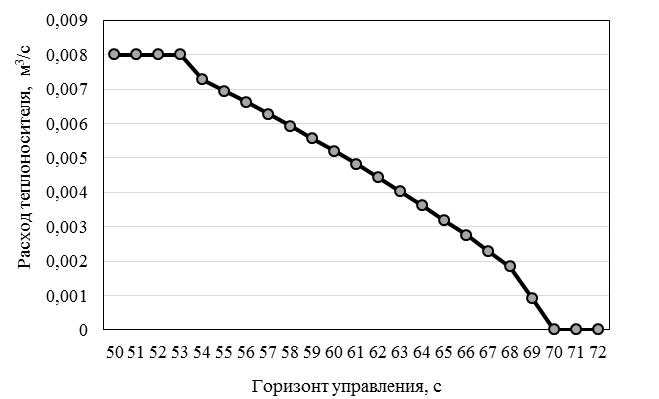
Рис. 5. Изменение расхода теплоносителя на участке горизонта управления
Fig. 5. Change in coolant flow rate in the control horizon area
Как и в задаче о быстродействии, управление носит кусочно-непрерывный характер. Управляющее воздействие u(t) принимает не только свои предельные значения (см. рис. 5). Объем затраченного теплоносителя составил 5,84 м3.
Заключение
Сравнительный анализ задач оптимального управления нагревом жидкого продукта жидким теплоносителем на основе принципа максимума показал, что управления могут принимать не только кусочно-непрерывные функции, но и описываться на участках горизонта управления гладкими непрерывными функциями, не имеющими разрывов. В случае задачи минимизации квадрата расхода теплоносителя, где управления принадлежат области допустимых ограничений, из принципа максимума следуют условия, полученные методами классического вариационного исчисления. Также очевидно, что для нагрева одного и того же объема продукта до заданной температуры при отсутствии потерь тепла в окружающую среду требуется одно и то же количество тепла (расход теплоносителя получился примерно одинаковым в обеих задачах). Поэтому учет теплообмена с окружающей средой может стать решающим в задаче оптимального управления нагревом продукта и подлежит дальнейшему исследованию.
1. Кудряшов В. С., Алексеев М. В., Юдаков А. А. Разработка математической модели стадии нагрева резиновой смеси и синтез алгоритма управления нагревом с использованием принципа максимума Понтрягина // Вестн. ВГУИТ. 2017. Т. 79. № 2. С. 80–87.
2. Плющаев В. И., Пахомов А. М. Модель системы стабилизации температуры продукта в емкости с переменной массой // Автоматизация и современные технологии. 2005. № 6. С. 25–28.
3. Плющаев В. И., Пахомов А. М. О динамических особенностях автоматической системы поддержания температурного режима в емкости с жидкой продукцией // Вестн. Волж. гос. акад. вод. транспорта. 2006. № 18. С. 178–185.
4. Кафаров В. В. Методы кибернетики в химии и химической технологии. М.: Химия, 1985. 448 с.
5. Понтрягин Л. С., Болтянский В. Г., Гамкрелидзе Р. В., Мищенко Е. Ф. Математическая теория оптимальных процессов. М.: Наука, 1983. 392 с.
6. Бахвалов Н. С. Численные методы. М.: БИНОМ. Лаборатория знаний, 2006. 636 с.
7. Бедарев И. А., Кратова Ю. В., Федорова Н. Н., Федорченко И. А. Методы вычислений в пакете Mathcad. Новосибирск, 2013. 163 с.
