Россия
Россия
Россия
Цель работы состоит в поиске путей совершенствования методов компьютерного моделирования и цифровизации выбора диагностических параметров сложных технических систем по максимуму информативности. Энтропийный способ оценки технического состояния систем основан на существовании функциональной зависимости случайных величин, характеризующих поведение элементов, всегда находящейся между двумя критическими состояниями: абсолютной целостности и полной аддитивности. Сложность взаимодействия элементов в стохастических системах определяет необходимость поиска для мониторинга и управления эффективных алгоритмов, базирующихся на фундаментальных энтропийных моделях и методах поиска наилучших решений. Модели и алгоритмы оценки параметров технического состояния и эксплуатационных показателей систем в процессе мониторинга совершенствуются на цифровой платформе MATLAB и ее приложениях. Отмечается, что для систем высокой сложности предлагается способ контроля, базирующийся на энтропийной оценке информации как наиболее универсальной и применимой в технических, биологических, экономических, социальных и иных си-стемах, трудно поддающихся аналитическому описанию и приемам формализации. Показано, что энтропийный способ выбора наиболее информативных узлов контроля при конструировании систем диагностики технических средств и технологических процессов на объектах водного транспорта позволяет значительно повысить надежность и обеспечить безотказность работы контролируемых объектов. Энтропийный способ оценки информативности, базирующийся на разности энтропий исходного и последующего состояний системы, применен для решения конкретных задач, приведенных в примерах. Предложен алгоритм ранжирования диагностических параметров на основе метода парных сравнений, на базе которого получена максимальная информативность выбранных диагностируемых узлов системы при минимальной совокупности контролируемых параметров.
автоматизация, диагностический параметр, информативность, контроль, энтропия, контролируемые параметры, попарная проверка
Введение
В условиях цифровизации открываются новые возможности совершенствования мониторинга технического состояния производственных объектов на водном транспорте, что позволяет повысить надежность и обеспечить безопасность эксплуатации сложного технологического оборудования и средств автоматики в широком диапазоне внешних воздействий. Цифровизация процессов мониторинга и контроля позволяет использовать для принятия решений способы и алгоритмы, построенные на использовании энтропийных моделей как наиболее универсальных, связанных с большими объемами обработки информации и реализуемых механизмами компьютерных систем [1–3].
Энтропийные модели применимы для оценки параметров и диагностики дефектов на ранних стадиях их проявления, что позволяет принимать превентивные решения по их исключению. Специфика энтропийных моделей позволяет исследовать системы с дефектами, содержащими самые различные внешние признаки, оказывающими влияние на диагностические параметры: образование нагара на контактных поверхностях электрических аппаратов; появление сколов и трещин в корпусах плат интегральных микросхем; загрязнения поверхностей механизмов и машин на судах, различных плавсредствах; негативные низкотемпературные проявления в межнавигационный период и другие, приводящие к необходимости совершенствования алгоритмов диагностирования [4].
Цифровизация мониторинга технического состояния объектов электроэнергетики и водного транспорта по параметрам, не поддающимся непосредственным измерениям, позволяет использовать косвенные методы оценки, базирующиеся на динамических наблюдателях переменных состояния по измерениям выходной координаты диагностируемого объекта, что дает возможность путем мажорирования сигналов определять техническое состояние датчиков информации и при возникновении признаков дефекта обеспечивать безаварийную работу объекта. Мониторинг технического состояния, базирующийся на энтропийных моделях, может быть усовершенствован путем формирования схем направленного выбора диагностируемых параметров из их совокупности, с учетом значимости по показателям информативности [5, 6]. В работе показана эффективность такого выбора.
Эффективность использования энтропии при моделировании систем обусловлена выбором критерия функционирования в каждом конкретном случае,
с учетом специфики объекта исследований [7, 8]. Поскольку полный контроль всех параметров практически неосуществим, на систему технической диагностики можно возложить контроль только некоторой части из множества наиболее информативных параметров [9, 10]. В этом случае выбор минимальной совокупности контролируемых параметров, отличающихся максимальной информативностью диагностируемых узлов системы, является важной и ответственной задачей повышения надежности и безотказности электрооборудования и электронных систем автоматики на объектах водного транспорта.
Методы и материалы
Для количественной оценки полноты контроля введем показатель Vпк, характеризующий информативность процесса при одновременном контроле Nk параметров (из всей совокупности N). В этом случае показатель Vпк определяется отношением количества информации к энтропии системы в исходном состоянии, т. е. до начала контроля [11–13]. В простейшем случае количественную оценку полноты контроля можно выполнить по формуле
![]()
Оценка информативности диагностических параметров выполняется на основе фундаментальных положений теории информации. В результате получаются количественные оценки вероятности нахождения диагностируемой системы в работоспособном состоянии, исследуются процессы изменения энтропии в процессе контроля параметров, определяются оптимальные решения путем рекурсивного выбора наиболее информативных узлов мониторинга системы. Используя формулу Шеннона
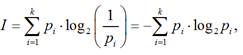 (1)
(1)
мы получаем оценку количества информации I по числу сообщений k и их вероятностям. Пусть электрическая система (объект) и каждый из ее функциональных элементов могут находиться в 2-х состояниях: работоспособном и неработоспособном. Вероятность нахождения системы в работоспособном состоянии Pс может быть оценена как вероятность работы всех ее n функциональных элементов ![]() , а вероятность нахождения системы в неработоспособном состоянии – как Qc = 1- Pc, где pi - вероятность безотказной работы i-го функционального элемента.
, а вероятность нахождения системы в неработоспособном состоянии – как Qc = 1- Pc, где pi - вероятность безотказной работы i-го функционального элемента.
Исходная неопределенность состояния системы (энтропия) до начала контроля диагностических параметров, согласно (1), равна
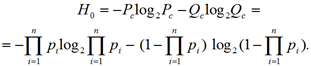 (2)
(2)
В результате контроля i-го элемента из n функциональных элементов системы проверяется только часть элементов nп ∈ n. В случае двух возможных результатов контроля параметров «в норме»
и «не в норме» вероятность нормы или положительного исхода контроля параметра составляет
![]()
Тогда неопределенность состояния системы, оставшаяся после того, как было установлено, что i-й параметр находится в норме, по аналогии с (2), будет равна
![]()
где nн – число непроверяемых элементов системы.
Информативность i-го параметра вычисляется как разность между исходной неопределенностью состояния системы H0 и неопределенностью , остающейся после контроля i-го параметра и усредненной по возможным исходам контроля
![]() (3)
(3)
При положительном результате проверки i-го параметра неопределенность состояния зависит только от вероятности безотказной работы ![]()
и вероятности отказа ![]() непроверенной группы элементов.
непроверенной группы элементов.
Информация, получаемая при одновременном контроле Nk диагностических элементов (из общего их числа N), позволяющих контролировать nп элементов системы, определяется аналогично (3):
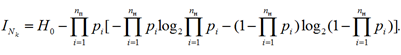
С учетом информативности контролируемых параметров полнота контроля может быть оценена по формуле
![]() (5)
(5)
При отсутствии количественных показателей безотказности элементов выбор диагностических параметров судового оборудования и электронной системы автоматики может быть выполнен путем опроса специалистов (экспертов) − опытных инженеров-электриков и электромехаников. С помощью метода экспертных оценок, используя опыт, знания и интуицию высококвалифицированных специалистов, можно, например, построить ранжированный (упорядоченный) ряд параметров, определяющих техническое состояние сложных систем.
При выборе параметров для контроля технического состояния объекта принимается во внимание, что требуемая полнота контроля определяется структурой его диагностической модели. В частном случае, когда все функциональные элементы схемы имеют по одному выходу, каждый из которых характеризуется одним физическим параметром (выходной функцией), диагностическая модель может совпадать с функциональной схемой объекта. В тех случаях, когда полный контроль технического состояния реализовать не представляется возможным, выбор контролируемых параметров сводится к определению такой совокупности доступных для контроля параметров, которая позволяла бы получить максимальное количество информации о состоянии объекта контроля. Использование энтропийного метода для выбора совокупности контролируемых параметров рассмотрим на конкретной задаче.
Решение задачи идентификации объекта и нахождения наиболее информативных параметров
Требуется найти минимальную совокупность контролируемых параметров из условия обеспечения работоспособности объекта диагностирования, функционально-структурная модель которого приведена на рис.
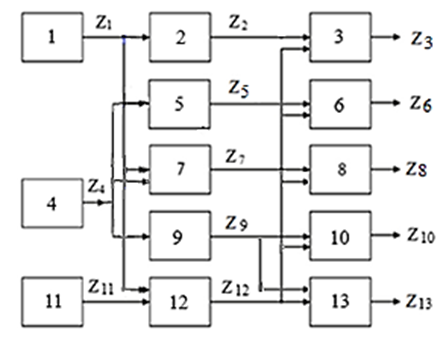
Функционально-структурная (диагностическая) модель объекта: 1–13 – элементы;
Z1, Z2, Z4, Z5, Z7, Z9, Z11, Z12 – параметрические функции элементов; Z3, Z6, Z8, Z10, Z13 – выходные параметрические функции элементов
Functional-structural (diagnostic) model of an object: 1–13 – elements;
Z1, Z2, Z4, Z5, Z7, Z9, Z11, Z12 – parametric functions of elements; Z3, Z6, Z8, Z10, Z13 – output parametric functions of elements
Для приведенной схемы условие работоспособности соответствует, в общем случае, исправному состоянию всех элементов. Требуется определить выходные функции, необходимые для полного контроля работоспособности системы Vпк = 1 и выбрать из 5 возможных попарно 2 выходные функции, контроль которых позволяет получить максимальную информацию о состоянии системы. Вероятности безотказной работы системы известны:
p1 = 0,95; p2 = 0,92; p3 = 0,90; p4 = 0,92; p5 = 0,99; p6 = 0,98; p7 = 0,97; p8 = 0,93; p9 = 0,95;
p10 = 0,94; p11 = 0,95; p12 = 0,97; p13 = 0,99.
Контролируемые параметры системы, обеспечивающие полноту диагностического контроля системы, будем искать из имеющегося набора выходных функций Z3, Z6, Z8, Z10 и Z13 модели (см. рис.), используя функциональную связь этих функций со всеми элементами диагностируемой системы, где знаком «+» отмечена зависимость выходов Zi от технического состояния соответствующего функционального элемента, а знаком «–» − ее отсутствие (табл.).
Зависимость выходных функций модели от технического состояния ее элементов
Dependence of the output functions of the model on the technical condition of its elements
|
Выходные |
Элементы диагностируемой модели |
||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
|
Z3 |
+ |
+ |
+ |
– |
– |
– |
– |
– |
– |
– |
+ |
+ |
– |
|
Z6 |
+ |
– |
– |
+ |
+ |
+ |
– |
– |
– |
– |
+ |
+ |
– |
|
Z8 |
+ |
– |
– |
+ |
– |
– |
+ |
+ |
– |
– |
+ |
+ |
– |
|
Z10 |
+ |
– |
– |
+ |
– |
– |
– |
– |
+ |
+ |
+ |
+ |
– |
|
Z13 |
+ |
– |
– |
+ |
– |
– |
– |
– |
+ |
– |
+ |
+ |
+ |
В общем случае алгоритм ранжирования диагностических параметров реализуется на основе метода парных сравнений, число которых равно числу возможных комбинаций попарных проверок (m = 2) выходных функций из общего их числа, равного nвых = 5, которое составит
![]() (6)
(6)
Алгоритм ранжирования диагностических параметров включает несколько этапов.
На первом этапе определяется исходная неопределенность состояния системы (энтропия H0) до начала контроля диагностических параметров. Система представлена 13 блоками (элементами). Если предположить, что отказ любого из 13 элементов системы приводит к отказу системы (переходу
в неработоспособное состояние), то исходная энтропия системы (при отсутствии контроля), в соответствии с формулой (2), будет равна
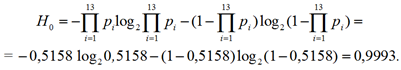
Процедуры (фрагменты программ) вычисления величины исходной энтропии H0, а также значений оставшейся энтропии после каждой попарной проверки выходных функций и информативности этих проверок, реализованные в кодах программно-вычислительной среды MATLAB, по просьбе редакции в статье не приводятся.
Затем на основе таблицы функциональных связей выходных функций модели со всеми элементами диагностируемой системы строится матрица Z связности модели той же размерности, что и таблица, но элементами которой являются не знаки «+» и «-», а единицы и нули соответственно:
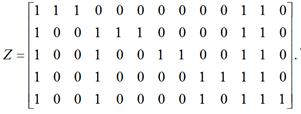
На втором этапе на основе построенной матрицы Z выполняется попарный контроль диагностических параметров (функций) пяти выходных элементов, целью которого является вычисление информативности и полноты контроля для каждой пары сравниваемых выходных функций (диагностических параметров) модели. С целью построения универсальной диагностической модели, не зависящей от размерности системы, определение контролируемых
и неконтролируемых элементов на каждом этапе попарного контроля выходных элементов будем проводить в цикле, задавая индекс первой в паре функции переменной i = 1, ..., 4 внешнего цикла, а индекс второй функции − переменной j = 2, …, 5 внутреннего цикла. В этом случае попарные проверки выходных функций повторяться не будут, а их количество будет соответствовать числу их возможных комбинаций C25 = 10, найденных по формуле (6).
При каждой попарной проверке происходит поэлементное сравнение с применением логической операции ИЛИ–НЕ [14] строковых векторов матрицы связности выходных функций по нулевым позициям, в результате чего получаем вектор V,
в котором единицы стоят на позициях непроверяемых элементов. Результаты попарных проверок, позволяющие получить вектор V для каждой возможной комбинации пар выходных функций, приведены ниже:
i = 1
V =
1×13 logical array
0 0 0 0 0 0 1 1 1 1 0 0 1
0 0 0 0 1 1 0 0 1 1 0 0 1
0 0 0 0 1 1 1 1 0 0 0 0 1
0 0 0 0 1 1 1 1 0 1 0 0 0
i = 2
V =
1×13 logical array
0 1 1 0 0 0 0 0 1 1 0 0 1
0 1 1 0 0 0 1 1 0 0 0 0 1
0 1 1 0 0 0 1 1 0 1 0 0 0
i = 3
V =
1×13 logical array
0 1 1 0 1 1 0 0 0 0 0 0 1
0 1 1 0 1 1 0 0 0 1 0 0 0
i = 4
V =
1×13 logical array
0 1 1 0 1 1 1 1 0 0 0 0 0
На том же этапе на основе вектора V формируются вспомогательные векторы Pa, состоящие из вероятностей безотказной работы проверяемых элементов, и Pb, состоящие из таких же вероятностей, но непроверяемых элементов. Вектор Pa имеет ту же размерность, что и вектор P0, но на позициях непроверяемых элементов содержит единицы:
Pa =
Columns 1 through 7
0.9500 1.0000 1.0000 0.9200 1.0000 1.0000 1.0000
Columns 8 through 13
1.0000 0.9500 0.9400 0.9500 0.9700 0.9900
Вектор Pb строится по обратному принципу: на позициях непроверяемых элементов вероятности их безотказной работы остаются, а на позициях проверяемых элементов содержатся единицы:
Pb =
Columns 1 through 7
1.0000 0.9200 0.9000 1.0000 0.9900 0.9800 0.9700
Columns 8 through 13
0.9300 1.0000 1.0000 1.0000 1.0000 1.0000
На третьем этапе алгоритма выполняется вычисление информативности попарного контроля диагностических параметров (функций) пяти выходных элементов. Для упрощения вычислений по формуле (4) информации о состоянии функциональной модели системы при одновременном контроле любой из пар выходных функций произведения вероятностей проверяемых и непроверяемых элементов модели выделены в отдельные блоки
A и B соответственно:
![]() (7)
(7)
в первом из которых выполняется произведение элементов вектора Pa, во втором − произведение элементов вектора Pb. Согласно синтаксису MATLAB операция произведения элементов вектора P выполняется с применением операторной функции prod(P), где P является аргументом этой функции. Таким образом, отдельные вычислительные блоки A и B, представленные формулами (7),
в рассматриваемом алгоритме реализованы через функции вида
A = prod(Pa); B = prod(Pb).
Тогда формулу (4) с учетом блочных преобразований (7) можно привести к упрощенному виду:
![]()
![]() . (8)
. (8)
Здесь же по известным значениям информативности попарных проверок, полученным из выражения (8), производится вычисление показателя полноты контроля всей системы по формуле (5).
Результаты
Результаты вычислений информативности контроля проверяемых пар выходных функций и показателя полноты контроля согласно алгоритму автоматизации формируются в массивах данных, состоящих из 4-х строк (i = 1, …, 4) и 5 столбцов
(j = 1, …, 5), т. е. размерности (4 × 5):
I =
0 0.5290 0.6442 0.6616 0.5765
0 0 0.4082 0.4218 0.3535
0 0 0 0.5248 0.4505
0 0 0 0 0.3948
v =
0 0.5294 0.6447 0.6621 0.5769
0 0 0.4085 0.4221 0.3538
0 0 0 0.5252 0.4509
0 0 0 0 0.3951
Отсюда, для вывода их значений с индексированными номерами проверяемых функций согласно предложенному алгоритму, осуществляется построчный вывод значений информативности I и показателя полноты контроля Vпк для каждой пары проверяемых функций:
Iv3_6 =
0.5290 0.5294
Iv3_8 =
0.6442 0.6447
Iv3_10 =
0.6616 0.6621
Iv3_13 =
0.5765 0.5769
Iv6_8 =
0.4082 0.4085
Iv6_10 =
0.4218 0.4221
Iv6_13 =
0.3535 0.3538
Iv8_10 =
0.5248 0.5252
Iv8_13 =
0.4505 0.4509
Iv10_13 =
0.3948 0.3951
Полученные результаты численных значений информативности I и показателя Vпк полноты контроля всех возможных попарных проверок служат для выбора такой пары выходных функций (контролируемых параметров), при которой обеспечивается наибольшая полнота контроля объекта диагностики. На основе предложенного алгоритма разработана программа, обеспечивающая автоматизацию вычислений показателей полноты контроля и информативности диагностируемых параметров при попарном сравнении всех выходных функций системы.
Таким образом, решена поставленная задача автоматизации расчета и выбора наиболее информативных параметров, обеспечивающих наибольшую полноту диагностического контроля объекта (системы) электроэнергетики. На этом работа алгоритма завершается.
Обсуждение
В результате сравнения результатов вычисления показателей I и Vпк по каждой паре проверяемых функций из 5 выходных, в качестве контролируемых параметров следует выбирать Z3 и Z10, при выборе которых достигается максимальная информативность выбранных диагностируемых узлов системы I = 0,6616 и наибольшая полнота контроля Vпк = 0,6621 при 2-х контролируемых параметрах.
Результаты численного моделирования параметров, оцениваемых с применением энтропийного способа оценки, получены в автоматическом режиме и полностью подтверждают работоспособность разработанной универсальной, не зависящей от размерности системы, диагностической модели выбора наиболее информативных узлов контроля системы.
Заключение
В работе приведены результаты исследований, связанные с построением и практической реализацией алгоритма автоматизации выбора наиболее информативных узлов контроля системы с применением энтропийного способа оценки информативности, базирующегося на разности энтропий исходного
и последующего состояний системы. По результатам исследований можно сделать следующие выводы:
1. Корректность и реализуемость предлагаемых технических решений подтверждена на примере эксперимента, состоящего из 10 сценариев попарных проверок контролируемых параметров (выходных функций).
2. Полученные оценки и решения с применением энтропийного способа позволяют осуществить выбор тех параметров, которые обеспечивают максимальную информативность выбранных диагностируемых узлов системы при минимальной совокупности контролируемых параметров.
3. Предложенный алгоритм автоматизации и численного моделирования процессов диагностического выбора диагностических параметров сложных технических систем по максимуму информативности на основе энтропийной оценки позволяет широко использовать инструментарий матричных преобразований в среде MATLAB для принятия обоснованных решений при обработке данных в системах автоматизированного управления и измерения на объектах водного транспорта.
4. Предложенные решения лежат в основе дальнейшего развития и совершенствования методов компьютерного моделирования и цифровизации диагностических проверок состояния сложных систем на водном транспорте по энтропийным критериям для использования в высокотехнологичных программно-измерительных комплексах автоматизированных систем управления. Это обусловлено тем, что в большинстве важных для практики случаев анализ вероятностных оценок технического состояния и работоспособности объектов и систем требует проведения множественных проверок, выполняемых с применением численных методов, для которых требуется инструментарий мощных программно-вычислительных сред. Примерами таких случаев являются процедуры нахождения информативных подмножеств признаков в регрессионном
и статистическом анализе, а также выявление отклонений параметров в автоматизированных системах управления.
Полученные численные результаты компьютерного моделирования подтверждают практическую направленность работы и возможность ее использования для решения широкого класса задач в исследуемой предметной области.
1. Гриб В. В., Жуков Р. В., Петрова И. М., Буяновский И. А. Диагностические модели изменения технического состояния механических систем: в 2 ч. М.: Изд-во МАДИ (ГТУ), 2007. Ч. 1. 300 с.; Ч. 2: 2008. 263 с.
2. Мосейко Е. С., Ольховик Е. О. Задачи оценки рисков и предупреждения отказов судовых механических систем // Вестн. Гос. ун-та мор. и реч. флота им. адм. С. О. Макарова. 2022. Т. 14 (6). С. 931-944.
3. Чертков А. А., Иванюк В. Ю., Каск Я. Н. Модальный синтез наблюдателя переменных состояния системы автоматики речного землесоса // Вестн. Гос. ун-та мор. и реч. флота им. адм. С. О. Макарова. 2022. Т. 14 (5). С. 787-797.
4. Синопальников В. А., Григорьев С. Н. Надежность и диагностика технологических систем. М.: Высш. шк., 2005. 343 с.
5. Кулаичев А. П. Методы и средства комплексного анализа данных. М.: ФОРУМ, ИНФРА-М, 2006. 512 с.
6. Вентцель Е. С., Овчаров Л. А. Теория случайных процессов и ее инженерные приложения. М.: Академия, 2009. 384 с.
7. Левич А. П. Энтропия как мера структурированности сложных систем // Время, хаос и математические проблемы: тр. семинара. М.: Изд-во Ин-та матем. исследований слож. систем МГУ им. М. В. Ломоносова, 2000. Вып. 2. С. 163-176.
8. Mobus G. E., Kalton M. C. Principles of Systems Science. Springer, 2015. 755 p.
9. Деева В. С., Романишина С. А., Слободян С. М. Устойчивость энтропийной оценки живучести систем // Изв. Том. политехн. ун-та. 2013. Т. 322, № 2. С. 67-72.
10. Лазарев В. Л. Исследование систем на основе энтропийных и информационных характеристик // Журн. техн. физики. 2010. Т. 80, вып. 2. С. 1-7.
11. Тырсин А. Н., Соколова И. С. Энтропийно-вероятностное моделирование гауссовских стохастических систем // Математическое моделирование. 2012. Т. 24, № 1. С. 88-103.
12. Noughabi H. A., Arghami N. R. A New Estimator of Entropy // Journal of Iranian Statistical Society. 2010. V. 9, iss. 1. P. 53-64.
13. Stowell D., Plumbley M. D. Fast Multidimensional Entropy Estimation by k-d Partitioning // IEEE Signal Pro-cessing Letters. 2009. V. 16, iss. 6. P. 537-540.
14. Иглин С. П. Математические расчеты на базе MATLAB. СПб.: БХВ-Петербург, 2005. 629 c.















