Moscow, Russian Federation
The methods for forecasting cyber threats and risk analysis using Bayesian models and Monte Carlo methods are considered in the article. Bayesian models have the capability to account for conditional probabilities and dynamically update estimates based on incoming data, ensuring a high degree of flexibility and adaptability in threat forecasting, particularly in conditions of uncertainty and a rapidly changing cyber environment. These models enable the consideration of the interrelationships between various factors and events, significantly enhancing the accuracy of predictions. Monte Carlo methods, through multiple simulations and scenario analysis, allow for a detailed assessment of risks and the likelihood of various events. The example of a Bayesian model structure that includes key elements of cybersecurity such as firewalls, malware, data breaches, social engineering, cloud services, and external networks. The results of Monte Carlo simulations reveal strong correlations between these elements. For instance, reduced firewall effectiveness increases the likelihood of malware infiltration, which, in turn, significantly raises the risk of data breaches. The success of social engineering attacks also greatly impacts the likelihood of data breaches. These identified interdependencies help in developing more precise and effective cybersecurity strategies by focusing efforts on critical nodes and potential vulnerability points. Such an approach enables cognitive security centers and cybersecurity experts to forecast threats, analyze risks, devise proactive defense measures, and make informed decisions aimed at enhancing the protection of critical infrastructure.
cybersecurity, cyber threat forecasting, Bayesian models, Monte Carlo methods, risk analysis, data leakage, social engineering
Введение
Развитие технологий приводит к увеличению угроз кибербезопасности, что создает значительные риски для информационных систем, сетей и критически важных инфраструктур. Центры безопасности обязаны своевременно прогнозировать и реагировать на эти угрозы, т. к. эффективное прогнозирование угроз является важнейшим компонентом обеспечения устойчивости и безопасности информационных систем [1].
Для прогнозирования угроз кибербезопасности используются различные подходы, которые включают в себя статистические методы, эвристические алгоритмы и методы машинного обучения [2].
Несмотря на свою популярность, каждый из этих методов имеет определенные ограничения. Эвристические алгоритмы могут оказаться недостаточно гибкими при появлении новых типов угроз [3], в то время как методы машинного обучения требуют больших объемов данных для обучения моделей, что не всегда возможно из-за ограничений конфиденциальности или нехватки данных [4]. Статистические методы часто не справляются с редкими событиями или сложными взаимосвязями между разными типами угроз [5].
Байесовские модели предлагают подход к прогнозированию угроз кибербезопасности путем включения в анализ вероятностных зависимостей и неопределенности. Эти модели позволяют динамически обновлять вероятности на основе новых данных, обеспечивая гибкую и адаптивную основу для прогнозирования угроз. В сочетании с методами Монте-Карло байесовские модели могут моделировать широкий спектр сценариев, обеспечивая более глубокий анализ и помогая выявить скрытые зависимости.
Методы Монте-Карло используют повторяющуюся случайную выборку для моделирования различных результатов, позволяя изучить с большей точностью более широкий спектр сценариев. Этот метод может дополнять байесовские модели, предоставляя обширное моделирование, которое помогает организациям лучше понять неопределенности и изменчивость, присущие угрозам кибербезопасности.
В статье рассматривается совместное применение байесовских моделей и методов Монте-Карло для прогнозирования угроз кибербезопасности. Эти подходы можно использовать для получения дополнительной информации об угрозах, поддержки принятия решений и повышения общей устойчивости информационных систем. Исследуя байесовскую модель, представляющую ключевые компоненты кибербезопасности, и применяя моделирование Монте-Карло, можно представить практическое применение этих методов в реальных сценариях кибербезопасности.
Байесовские модели
Байесовские модели представляют собой класс статистических моделей, основанных на теореме Байеса, которая определяет способ обновления вероятностей событий на основе новой информации [6]:
P(A|B) = P(B|A) · P(A) / P(B),
где P(A|B) – условная вероятность события A при наличии информации B; P(B|A) – условная вероятность B при наличии A; P(A) – априорная вероятность события A; P(B) – полная вероятность информации B.
Байесовские модели используются для прогнозирования киберугроз путем взаимодействия исторических данных (априорных вероятностей) с новой информацией (доказательствами). Эти модели представляются в виде направленных ациклических графов (DAG), где узлы обозначают события или переменные, а ребра показывают причинно-следственные связи. Предложим ацикличный граф для байесовской модели для прогнозирования киберугроз (рис. 1).
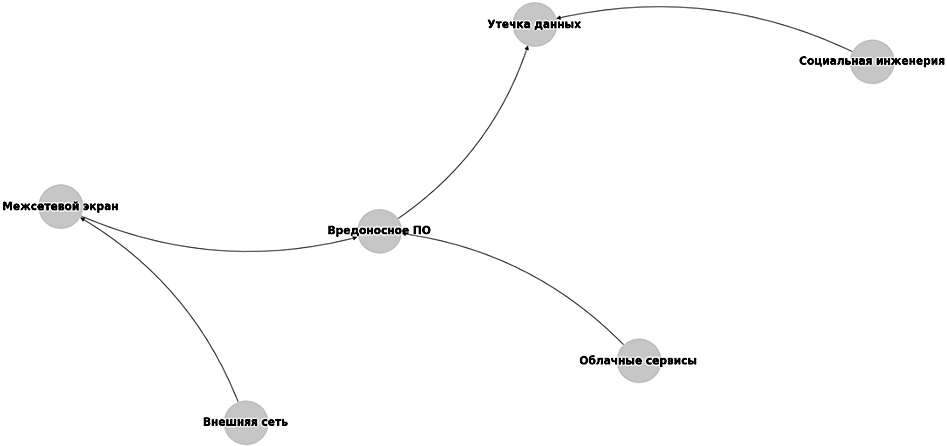
Рис. 1. Байесовская модель для прогнозирования киберугроз
Fig. 1. Bayesian model for forecasting cyber threats
Узлы модели:
– межсетевой экран. Основная задача заключается в фильтрации внешнего трафика и предотвращении проникновения вредоносного ПО;
– вредоносное ПО. Вероятность проникновения вредоносного ПО в систему;
– утечка данных. Вероятность утечки данных из-за присутствия вредоносного ПО или успешного воздействия социальной инженерии;
– социальная инженерия. Узел, представляющий риск, связанный с манипуляцией людьми для получения несанкционированного доступа;
– облачные сервисы. Возможные риски при использовании облачных сервисов;
– внешняя сеть. Уязвимости, возникающие из-за проникновения через внешний периметр.
Ребра модели представляют условные зависимости:
– «межсетевой экран» влияет на «вредоносное ПО»;
– «вредоносное ПО» влияет на «утечку данных»;
– «социальная инженерия» также влияет на «утечку данных»;
– «облачные сервисы» могут повлиять на «вредоносное ПО»;
– «внешняя сеть» влияет на «межсетевой экран».
Связь графа с байесовской моделью:
1. Условная вероятность вредоносного ПО.
Если межсетевой экран малоэффективен, то вероятность проникновения вредоносного ПО увеличивается.
Условная вероятность P(«Вредоносное ПО»|«Межсетевой экран») определяется зависимостью между этими узлами.
2. Условная вероятность утечки данных.
При наличии вредоносного ПО и успешного воздействия социальной инженерии вероятность утечки данных возрастает:
P(«Утечка данных»| «Вредоносное ПО»); P(«Утечка данных»| «Социальная инженерия»).
С помощью байесовских моделей можно прогнозировать вероятности различных киберугроз, учитывая условные зависимости между узлами.
Байесовские модели оценивают риски угроз в реальном времени при получении новых данных. Например, если межсетевой экран малоэффективен, происходит пересчет вероятностей и когнитивный центр безопасности принимает соответствующие меры.
Байесовский граф позволяет оценить вероятность киберугроз, выявить взаимосвязи и прогнозировать инциденты.
Методы Монте-Карло
Методы Монте-Карло – это класс алгоритмов, которые используют случайные или псевдослучайные числа для выполнения вычислений и симуляций [7]. Эти методы применяются для решения задач, требующих обработки сложных систем и неопределенности. В кибербезопасности методы Монте-Карло применяются для анализа рисков, оценки вероятностей различных событий и прогнозирова
ния возможных угроз и атак.
Основной принцип метода Монте-Карло заключается в многократном выполнении симуляций и последующем анализе результатов. Формула для оценки вероятностей с использованием метода Монте-Карло:
P(A) = NA / N,
где P(A) – априорная вероятность события A; NA – количество произошедших событий A в симуляциях; N – общее количество симуляций.
Рассмотрим применение метода Монте-Карло для оценки рисков в кибербезопасности. Для оценки вероятности успешной кибератаки и утечки данных необходимо выполнить несколько тысяч симуляций.
Симуляция кибератаки. Генерируем случайные выборки, представляющие возможные кибератаки. Каждая симуляция моделирует возможность успешной или неуспешной атаки, основываясь на заданной вероятности.
Симуляция утечки данных. После каждой симуляции кибератаки происходит моделирование вероятности утечки данных.
После выполнения симуляций представляется визуализация распределений вероятностей и корреляции между различными событиями (рис. 2).
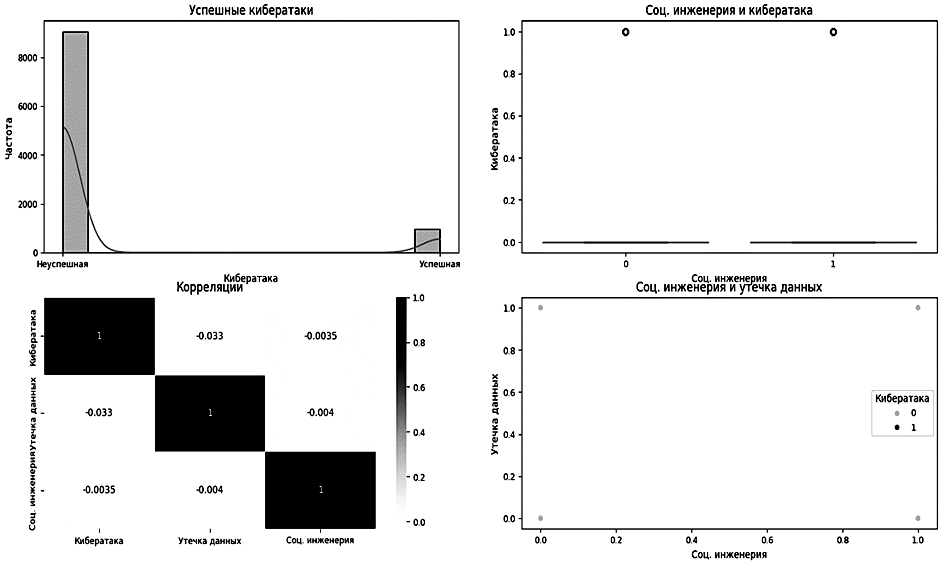
Рис. 2. Визуализация распределений вероятностей и корреляции
Fig. 2. Visualization of probability distributions and correlations
Гистограмма успешных кибератак отображает распределение успешных и неуспешных кибератак.
Box Plot для социальной инженерии и кибератаки позволяет оценить влияние социальной инженерии на кибератаки.
Тепловая карта корреляций показывает корреляции между переменными, помогая выявить взаимосвязи.
Диаграмма рассеяния отображает связь между социальной инженерией и утечками данных, учитывая кибератаки.
Сочетание байесовских моделей и методов Монте-Карло позволяет комплексно решать вопрос кибербезопасности:
– моделировать сложные системы: байесовские модели создают причинно-следственные связи между переменными, а методы Монте-Карло позволяют проводить симуляции для оценки вероятностей
событий;
– обновлять вероятности: используя методы Монте-Карло, можно обновлять вероятности в байесовской модели, выполняя множество симуляций и анализируя результаты, это помогает уточнить оценки на основе новых данных;
– анализировать риски: с помощью симуляций можно оценить риски кибератак, утечек данных или других угроз, а байесовская модель позволяет установить причинно-следственные связи между различными переменными.
Взаимодействие байесовской модели и метода Монте-Карло представлено на рис. 3.
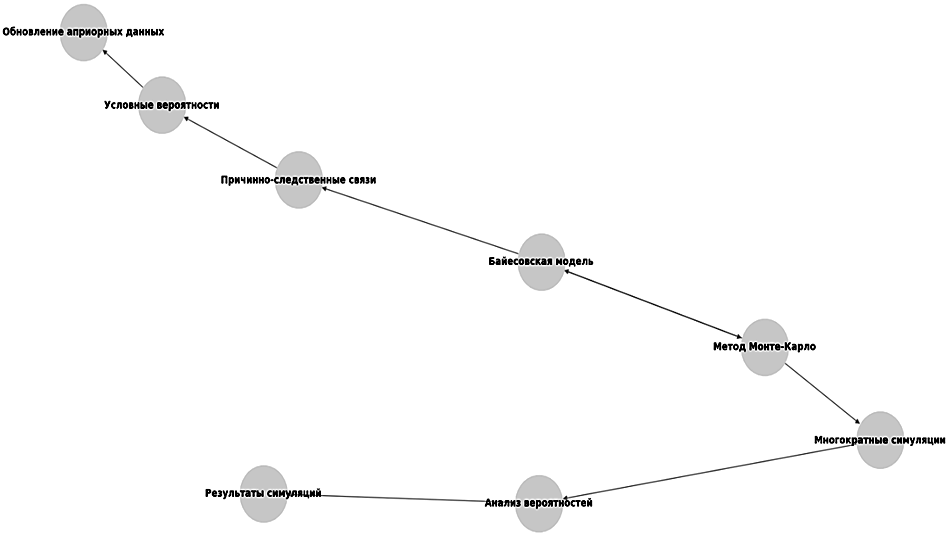
Рис. 3. Байесовская модель и метод Монте-Карло
Fig. 3. The Bayesian model and the Monte Carlo method
Узлы представляют компоненты байесовской модели и метода Монте-Карло, а ребра показывают причинно-следственные связи между ними, а также этапы, которые соединяют два метода.
Узлы байесовской модели:
– «Байесовская модель» – главный узел, указывающий на структуру модели;
– «Причинно-следственные связи» обозначает структуру DAG в байесовской модели;
– «Условные вероятности» представляет вероятность зависимостей между узлами;
– «Обновление априорных данных» отражает коррекцию вероятностей на основе новых данных.
Узлы метода Монте-Карло:
– «Метод Монте-Карло» – основной узел, указывающий на метод симуляций;
– «Многократные симуляции» представляет запуск симуляций методом Монте-Карло;
– «Анализ вероятностей» указывает на анализ результатов симуляций;
– «Результаты симуляций» обозначает обработку данных после симуляций.
Ребра между узлами:
- Байесовская модель:
– «Байесовская модель» соединяется с «Причинно-следственными связями», обозначая создание структуры DAG;
– «Причинно-следственные связи» соединены с «Условными вероятностями», отражая обновление условных вероятностей;
– «Условные вероятности» ведут к «Обновлению априорных данных», обозначая коррекцию априорных вероятностей.
- Метод Монте-Карло:
– «Метод Монте-Карло» соединяется с «Многократными симуляциями», указывая на запуск симуляций;
– «Многократные симуляции» соединены с «Анализом вероятностей», что означает анализ результатов симуляций;
– «Анализ вероятностей» соединен с «Результатами симуляций», представляя обработку данных.
Ребра, соединяющие «Байесовскую модель» и «Метод Монте-Карло», показывают, как структура DAG передается для запуска симуляций, а результаты симуляций возвращаются для обновления байесовской модели.
Граф демонстрирует, как байесовская модель создает причинно-следственные связи, а метод Монте-Карло используется для симуляций, анализа рисков и прогнозирования вероятностей. Взаимодействие этих методов позволяет эффективно обновлять вероятности в реальном времени, проводить анализ и разрабатывать стратегии для кибербезопасности.
Применение метода Монте-Карло к байесовской модели кибербезопасности
Применение метода Монте-Карло к байесовской модели позволяет оценить вероятность киберугроз и проанализировать риски, связанные с условными зависимостями в модели. Начальные условные вероятности в модели задаются на основании исторических данных, экспертных оценок и статистических показателей прошлых инцидентов. Эти вероятности, определяемые специалистами по кибербезопасности и аналитиками, обеспечивают основу для дальнейшего моделирования и анализа.
Типы данных, используемых для задания начальных условных вероятностей:
1. Исторические данные:
– журналы безопасности: лог-файлы и отчеты о прошлых инцидентах, где документированы случаи атак, успешных и неуспешных попыток проникновения, а также типы угроз, с которыми сталкивалась организация (журнал событий межсетевого экрана из отчета Gartner Magic Quadrant for Network Firewalls, 2023);
– статистика уязвимостей: данные об известных уязвимостях в системах, программном обеспечении и сетевой инфраструктуре. Например, сколько раз определенная уязвимость была эксплуатирована, как часто происходили попытки эксплуатации и каковы были последствия (аналитический отчет по угрозам Symantec Internet Security Threat Report, 2022);
– отчеты об инцидентах: официальные документы, описывающие подробности о прошлых инцидентах, включая тип атаки, используемые методы и стратегии атакующих и последствия для организации (анализ утечек данных в IBM Cost of a Data Breach Report, 2023).
2. Экспертные оценки:
– мнение специалистов: оценки экспертов по кибербезопасности, которые опираются на их профессиональный опыт, знания об актуальных угрозах и понимание конкретной архитектуры и уязвимостей информационных систем организации (опрос экспертов по результатам последнего годового обзора безопасности от ISACA State of Cybersecurity Report, 2023);
– оценки вероятности: эксперты могут предоставлять количественные оценки вероятностей возникновения различных событий на основе их опыта и знаний о текущих трендах в киберугрозах (оценка вероятности успеха фишинговых атак в отчете Verizon 2023 Data Breach Investigations Report);
– анализ рисков: комплексный анализ потенциальных рисков с учетом текущих и прогнозируемых угроз, а также методов защиты, используемых в организации (доклад по результатам анализа рисков от NIST Risk Management Framework (RMF) guidelines).
3. Статистические показатели прошлых инцидентов:
– частота инцидентов: данные о частоте различных типов инцидентов, таких как успешные проникновения через межсетевой экран, случаи социальной инженерии и успешные атаки вредонос-
ного ПО (отчеты о кибербезопасности от Microsoft Digital Defense Report, 2023);
– успешность защиты: статистика, показывающая, насколько эффективно использовались существующие меры защиты в прошлых случаях и как это влияет на общую безопасность системы (статистика успешности блокировки вредоносного ПО антивирусной системой от AV-TEST Annual Report, 2023);
– временные тренды: анализ изменений в частоте и типах инцидентов со временем, чтобы учитывать динамику развития угроз и адаптацию защитных мер (тренды инцидентов безопасности в отчете ENISA Threat Landscape Report, 2023).
- Исходные данные для модели:
– межсетевой экран: эффективность 90 %, неэффективность 10 %, источник данных – журналы и отчеты безопасности, оценки экспертов по уровню фильтрации нежелательного трафика и блокировки атак (журнал событий межсетевого экрана из отчета Gartner Magic Quadrant for Network Firewalls, 2023);
– социальная инженерия: успех 30 %, неудача 70 %, источник данных – опросы сотрудников, оценки успешности фишинговых кампаний, исторические данные о попытках социальной инженерии (отчет о результатах фишинговых кампаний в рамках исследования Verizon 2023 Data Breach Investigations Report (DBIR);
– вредоносное ПО: успех проникновения 20 %, неуспех 80 %, источник данных – cтатистические отчеты о случаях обнаружения и предотвращения вредоносного ПО, оценка эффективности антивирусных систем (аналитический отчет по угрозам Symantec Internet Security Threat Report, 2022);
– утечка данных: успех 40 %, неуспех 60 %, источник данных – исторические инциденты утечек данных, анализ уязвимостей в системе хранения и передачи данных (анализ утечек данных в IBM Cost of a Data Breach Report, 2023);
– облачные сервисы: успех проникновения 10 %, неуспех 90 %, источник данных – отчеты о безопасности облачных сервисов, статистика атак на облачные инфраструктуры (обзор безопасности облачных инфраструктур в Gartner Cloud Security Report, 2023);
– внешняя сеть: уязвимость 15 %, надежность 85 %, источник данных – анализ журналов доступа, данные о попытках несанкционированного доступа через внешние сети, оценки безопасности от сторонних поставщиков (журнал доступа через внешние сети от Qualys Vulnerability Management Report, 2023).
Для оценки вероятности проникновения вредоносного ПО метод Монте-Карло проводит 100 000 симуляций, варьируя эффективность межсетевого экрана. В каждой симуляции эффективность межсетевого экрана может изменяться в диапазоне от 80 до 95 %. Это позволяет оценить, как вероятность проникновения вредоносного ПО меняется в зависимости от этой эффективности.
Каждая симуляция – это возможный сценарий, который включает условные зависимости между узлами. В симуляции, где межсетевой экран эффективен на 90 %, вероятность проникновения вредоносного ПО 20 %. В такой ситуации утечка данных происходит реже, т. к. проникновение вредоносного ПО менее вероятно. Однако если эффективность межсетевого экрана падает до 80 %, вероятность проникновения вредоносного ПО возрастает до 35 %. В результате риск утечки данных повышается (рис. 4).
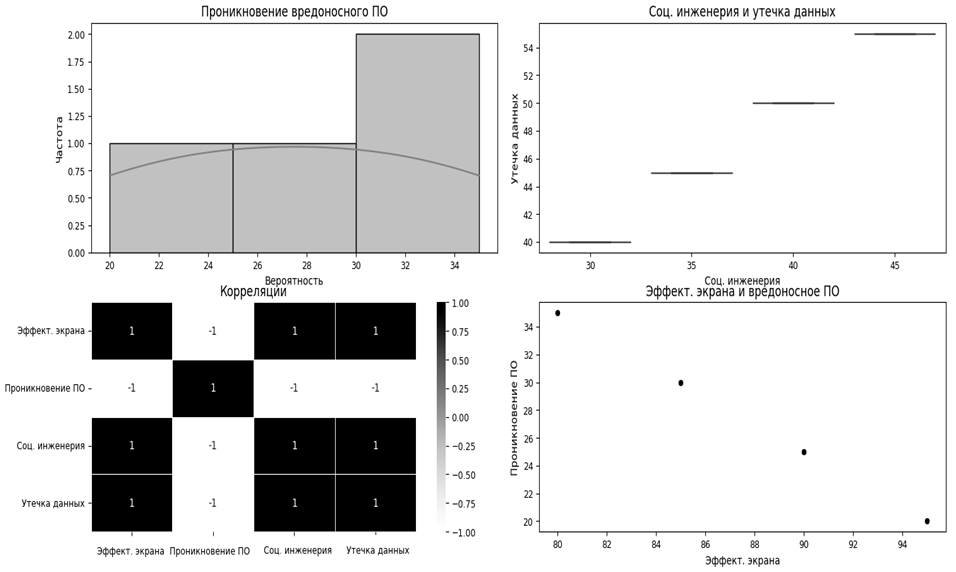
Рис. 4. Применение метода Монте-Карло к байесовской модели
Fig. 4. Application of the Monte Carlo method to the Bayesian model
Если симуляции показывают, что успешная социальная инженерия в 30 % случаев приводит к проникновению вредоносного ПО, это сигнализирует о потенциальных рисках для системы кибербезопасности. Если успешность социальной инженерии повышается до 40 %, вероятность утечки данных увеличивается пропорционально, что указывает на необходимость усиления мер противодействия социальной инженерии.
Если результаты симуляций показывают, что успешная социальная инженерия часто связана с проникновением вредоносного ПО, это может означать, что связь между этими узлами сильнее, чем предполагалось. Это также может означать, что успешная социальная инженерия повышает риск утечки данных.
Если утечка данных часто связана с определенным уровнем эффективности межсетевого экрана, это может указывать на уязвимости в системе, которые требуют дополнительного внимания.
Дополнительные аспекты и выводы
Влияние изменений в уровне защиты на вероятность проникновения:
– при эффективности межсетевого экрана на уровне 85 % и успешной социальной инженерии в 30 % вероятность проникновения вредоносного ПО может увеличиться до 25 %, что указывает на важность комплексного подхода к защите от различных угроз;
– при уровне защиты на 95 % и успешной социальной инженерии в 40 % вероятность проникновения вредоносного ПО может снизиться до 15 %, что подчеркивает значимость высокоэффективных мер безопасности.
Расширение сценариев успешной атаки:
– если успешная социальная инженерия часто сопровождается проникновением вредоносного ПО, это может указывать на слабые места в обучении персонала или необходимость усиления мониторинга поведения пользователей;
– анализ таких сценариев помогает выявить уязвимые зоны в системе и разработать целевые меры для усиления защиты.
Учет изменяющихся угроз:
– с учетом быстро меняющейся угрозовой среды необходимо периодически обновлять модель и включать новые данные для более точной оценки рисков;
– регулярное обновление модели позволяет адаптировать стратегии кибербезопасности к новым угрозам и обеспечивать высокий уровень защиты.
Итеративное улучшение защиты. Использование метода Монте-Карло для моделирования различных сценариев помогает оценить эффективность предпринимаемых мер безопасности и идентифицировать области для улучшения. Например, если утечка данных часто связана с определенным уровнем эффективности межсетевого экрана, это может стать причиной для улучшения настроек и мониторинга данного узла.
Управление рисками на основе данных. Анализ данных и моделирование с помощью Монте-Карло способствуют разработке эффективных стратегий управления рисками, основанных на реальных данных и конкретных сценариях атак.
Это позволяет более точно прогнозировать возможные последствия инцидентов и предпринимать проактивные меры по защите информационной безопасности.
Применение метода Монте-Карло к байесовской модели помогает понять, как различные параметры влияют на риск утечки данных и других киберугроз. Моделируя различные сценарии, можно выявить критические узлы и ребра, которые требуют особого внимания, и разработать более эффективные стратегии кибербезопасности.
Заключение
В статье исследовалось применение байесовских моделей и методов Монте-Карло для прогнозирования угроз кибербезопасности. Сочетание этих методов создает основу для понимания сложных зависимостей и оценки вероятности различных угроз кибербезопасности. Байесовские модели с их способностью обновлять вероятности на основе новых данных обеспечивают гибкость при прогнозировании угроз. Методы Монте-Карло позволяют проводить анализ рисков и тем самым дополняют байесовские модели, обеспечивая более глубокое понимание потенциальных сценариев угроз.
Результаты исследования позволили изучить взаимосвязи между различными компонентами модели кибербезопасности. Например, эффективность межсетевого экрана существенно влияет на вероятность проникновения вредоносного ПО, при этом более низкая эффективность коррелирует с более высоким риском проникновения вредоносного ПО. Кроме того, успех социальной инженерии играет решающую роль в определении вероятности утечки данных, что указывает на необходимость уделять больше внимания как техническим, так и человеческим аспектам в стратегиях кибербезопасности.
Анализируя различные сценарии, можно выявить критические зависимости, оценить риски и понять, как различные факторы влияют на вероятность различных угроз кибербезопасности.
Этот подход может помочь в принятии решений и разработке более эффективных стратегий снижения рисков и реагирования на возникающие угрозы.
Использование байесовских моделей позволяет получить вероятностное понимание угроз кибербезопасности, а методы Монте-Карло позволяют исследовать неопределенность и изменчивость внутри системы. Этот подход может помочь разработать более эффективные стратегии и принять обоснованные решения, которые будут способствовать укреплению кибербезопасности.
1. Tsibizova T. Iu., Panilov P. A., Kocheshkov M. A. Monitoring bezopasnosti sistemy zashchity informatsii kriticheskoi informatsionnoi infrastruktury na osnove kognitivnogo modelirovaniia [Monitoring the security of the information security system of the critical information infrastructure based on cognitive modeling]. Izvestiia Tul'skogo gosudarstvennogo universiteta. Tekhnicheskie nauki, 2023, no. 6, pp. 33-41. DOI:https://doi.org/10.24412/2071-6168-2023-6-33-41.
2. Panilov P. A., Tsibizova T. Iu., Voskresenskii G. A. Metodologiia ekspertno-agentnogo kognitivnogo modeliro-vaniia preduprezhdeniia vozdeistviia na kriticheskuiu informatsionnuiu infrastrukturu [Methodology of expert-agent cognitive modeling of prevention of impact on critical information infrastructure]. Kliuchevye trendy razvitiia iskusstvennogo intellekta: nauka i tekhnologii: Mezhdunarodnaia IT-konferentsiia (Moskva, 21 aprelia 2023 g.). Moscow, Izd-vo MGTU im. N. E. Baumana, 2023. Pp. 98-104.
3. Markov A. S., Matveev V. A., Fadin A. A., Tsirlov V. L. Evristicheskii analiz bezopasnosti programmnogo koda [Heuristic analysis of program code security]. Vestnik Moskovskogo gosudarstvennogo tekhnicheskogo universiteta im. N. E. Baumana. Seriia: Priborostroenie, 2016, no. 1 (106), pp. 98-111.
4. Pechenkin A. I., Zegzhda D. P. Primenenie metodov mashinnogo obucheniia i intellektual'nogo analiza v zadachakh informatsionnoi bezopasnosti [Application of machine learning and intelligent analysis methods in information security tasks]. Metody i tekhnicheskie sredstva obespecheniia bezopasnosti informatsii, 2017, no. 26, p. 48.
5. Nesterenko V. A. Statisticheskie metody obnaruzhe-niia narushenii bezopasnosti v seti [Statistical methods for detecting network security breaches]. Informatsionnye protsessy, 2006, vol. 6, no. 3, pp. 208-217.
6. Dorozhko I. V., Zakharova E. A., Osipov N. A. Model' dlia otsenki veroiatnosti bezotkaznoi raboty slozhnykh tekhnicheskikh kompleksov na osnove dinamicheskikh baiesovskikh setei [A model for estimating the probability of trouble-free operation of complex technical complexes based on dynamic Bayesian networks]. Trudy Voenno-kosmicheskoi akademii imeni A. F. Mozhaiskogo, 2019, no. 669, pp. 216-223.
7. Shumkov M. A. Metod Monte-Karlo v matematich-eskoi statistike [The Monte Carlo method in mathematical statistics]. Nauchnye issledovaniia i razrabotki studentov: sbornik materialov IV Mezhdunarodnoi studencheskoi nauchno-prakticheskoi konferentsii (Cheboksary, 29 iiunia 2017 g.). Cheboksary, OOO «Tsentr nauchnogo sotrudnichestva "Interaktiv plius"», 2017. Pp. 220-222.

















