Russian Federation
from 01.01.2023 until now
Russian Federation
In the paper the experimental induction heating installation for through heating of steel cylindrical workpieces is considered. It is well known that the use of an industrial heating system presupposes incomplete information about its main characteristics due to the complex nature of changes in some parameters both from the ambient temperature and from the temperature of the heated part. These parameters primarily include the coefficients of convective and emissive heat transfer from the surface of the workpiece. At the first step, it is necessary to obtain the values of unknown parameters, which also include the voltage of the power source, and then solve the optimal control problem. The problem of identifying these parameters is solved using the alternance method of parametric optimization of systems with distributed parameters, using experimental data from thermocouples. The obtained values of unknown parameters are then used in a numerical finite-element FLUX model of the considered process. Based on the developed model, the problem of time-optimal control with an additional phase restriction on the maximum temperature is formulated. This problem is solved using the alternance method. The solution of the problem made it possible to obtain a emperature field with a maximum deviation of 32 °C from the required temperature T* = 1 200 °C. This value is less than 3% of the desired temperature value and fully meets the technological requirements for induction through heating processes prior subsequent plastic deformation. The maximum temperature in this case does not exceed the maximum permissible value of 1 300 °C during the entire heating process.
induction heating, numerical simulation, Altair FLUX, alternance method, parametric identification, optimal control
Введение
В настоящее время стремительно увеличивается темп развития отраслей тяжелой промышленности, в связи с этим возрастает роль применения различных электротермических установок и печей. В металлургии наиболее широкое распространение получили индукционные нагревательные установки, которые применяются для таких технологических операций, как плавка металла, пайка, отжиг, штамповка и прокатка, поверхностная и глубокая закалка металла. Подобное широкое применение индукционных печей обуславливается рядом преимуществ перед другими видами нагрева: большая скорость нагрева, уменьшение образования окалины, малые габариты нагревательных установок, отсутствие необходимости предварительного разогрева печи, высокая экологичность процесса нагрева, обусловленная отсутствием продуктов сгорания. Развитие отраслей тяжелой промышленности приводит к необходимости повышения экономической эффективности производственных процессов, как правило, достигаемого за счет ужесточения требований к конечному состоянию полуфабриката. Указанная проблема может быть решена с помощью оптимизации конструктивных характеристик или режимов работы индукционного нагревателя по соответствующим критериям качества. Решение задачи оптимального управления возможно только при наличии полной информации об объекте. Однако в технологических процессах термообработки ряд параметров оказывается известен только с точностью до возможных диапазонов их изменения, что обуславливает необходимость установления их конкретных значений. В работе рассматривается решение задачи параметрической идентификации коэффициентов теплообмена с поверхности стальной детали на основе экспериментальных данных, полученных на лабораторной нагревательной установке, на базе численной модели, построенной в пакете Altair FLUX. Установленные значения параметров используются при решении задачи оптимального по быстродействию управления в условиях наличия фазового ограничения на максимальную температуру поверхности обрабатываемой детали.
Параметрическая идентификация процесса индукционного нагрева
В работе рассматривается лабораторная установка для сквозного индукционного нагрева цилиндрических деталей из стали С40 [1, 2], сконструированная в Институте электротехнологий Университета им. Лейбница (г. Ганновер) (рис. 1, а).
а б
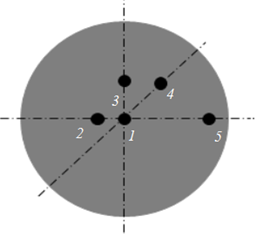
Рис. 1. Лабораторная нагревательная установка: а – общий вид; б – места установки термопар:
1 (0; 0); 2 (–11; 0); 3 (0; 22); 4 (23; 23); 5 (44; 0)
Fig. 1. Laboratory heating installation: a – general view; б – location of thermocouples:
1 (0; 0); 2 (–11; 0); 3 (0; 22); 4 (23; 23); 5 (44; 0)
Для контроля температуры на глубине 25 мм от торца заготовки установлено 5 хромель-алюмелевых термопар (см. рис. 1, б). Основные геометрические параметры установки приведены в табл. 1.
Таблица 1
Table 1
Основные параметры индукционной нагревательной системы
Main parameters of induction heating system
|
Параметр |
Значение |
|
Длина индуктора, м |
0,08 |
|
Количество витков индуктора, шт. |
5 |
|
Радиус заготовки R, м |
0,05 |
|
Длина заготовки L, м |
0,095 |
|
Расстояние между индуктором и заготовкой H, м |
0,005 |
|
Расстояние между витками индуктора h, м |
0,005 |
|
Геометрические размеры витка индуктора A × B, м |
0,006 × 0,012 |
|
Материал заготовки |
Сталь (С40) |
|
Частота питающего тока f, кГц |
125 |
|
Температура окружающей среды Токр, °С |
25 |
Как уже было отмечено, для решения задачи оптимального управления указанным объектом необходимо иметь полную информацию о его характеристиках, включая коэффициенты теплообмена αконв, αизл с поверхности детали. Конструкция экспериментальной установки предполагает управление мощностью генератора, поэтому конкретное значение напряжения U источника питания также является неизвестным.
Восстановление искомых коэффициентов проводится на основе решения обратной задачи индукционного нагрева [3, 4]. В ее постановке полагается, что значения идентифицируемых параметров неизвестны, и их требуется установить на основе дополнительной информации о температурном распределении, полученной на интервале идентификации в одной точке термометрирования с координатами (44; 0), соответствующих термопаре № 5 на рис. 1, б. Выбор этой термопары объясняется максимальной ее близостью к боковой поверхности изделия.
Для поиска искомых коэффициентов был применен метод параметрической оптимизации, позволяющий восстанавливать неизвестные величины на множествах физически реализуемых достаточно гладких функций, что обосновано физической сущностью процесса.
Поскольку поиск искомых коэффициентов проводился на множестве постоянных функций, вектор идентифицируемых параметров имеет следующий вид: 
.
Параметризованное представление температурного поля, зависящего от искомых коэффициентов, используется в двумерной численной модели процесса, построенной в пакете Altair FLUX. Подробно процесс построения модели описан в [5–7]. Общий вид FLUX-модели со сгенерированной конечно-элементной сеткой показан на рис. 2.
Рис. 2. Геометрия нагревательной системы
с конечно-элементной сеткой в Altair FLUX
Fig. 2. Geometry of heating system
with finite-element mesh in Altair FLUX
Построенная FLUX-модель используется для численного моделирования температурной кривой 
на том же интервале идентификации 
в точке с пространственными координатами x* = 44 мм, y* = 0 мм. Формулируется задача оптимального управления с минимаксным критерием оптимальности при оценивании температурной невязки между экспериментальными данными и модельной реализацией в равномерной метрике:
(1)
Таким образом, задача параметрической идентификации предусматривает поиск такого вектора параметров 
, обеспечивающего восстановление искомых коэффициентов на априори заданных классах решения, при котором достигается минимаксное значение критерия оптимальности (1).
Решение сформулированной задачи получено с помощью альтернансного метода, который позволяет свести искомую задачу к системе трансцендентных уравнений, замкнутых относительно всех неизвестных параметров процесса [8, 9]. В рассматриваемом случае вектор содержит 3 параметра, что, согласно теории метода, соответствует 4-м точкам с максимальным отклонением кривой
от данных эксперимента T*(t). Поскольку моменты времени tj, в которые достигаются указанные отклонения, заранее неизвестны, система уравнений дополняется необходимыми условиями экстремума в них.
Таким образом, искомая система уравнений альтернансного метода имеет следующий вид:
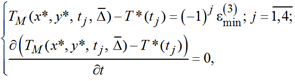(2)
где величина 
соответствует минимальному абсолютному отклонению модельной температуры от экспериментальной, достижимому в классе задач с тремя искомыми параметрами. Указанная система из 8 уравнений оказывается замкнутой относительно всех неизвестных параметров, к которым относятся три компоненты вектора , величина , а также неизвестные моменты времени 
.
В результате численного решения системы уравнений (2) были получены следующие результаты (табл. 2).
Таблица 2
Table 2
Результаты параметрической идентификации
Results of parametric identification
|
Параметр |
Значение |
|
Конвективный коэффициент теплообмена αконв, Вт/м2∙°С |
70 |
|
Коэффициент теплообмена излучением αизл, Вт/м2∙°С4 |
0,66 |
|
Напряжение источника питания, В |
175 |
Кривая отклонения 
температуры, полученной в численной модели FLUX,
от экспериментальных данных показана на рис. 3..
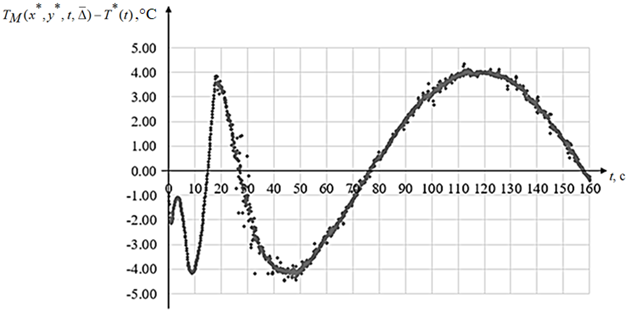
Рис. 3. Кривая температурного отклонения после идентификации неизвестных параметров
Fig. 3. Temperature deviation curve after parameters identification
Из анализа результатов следует, что величина предельного отклонения модельной температуры от экспериментальных данных 
составляет не более 1 % от максимальной температуры нагрева заготовки.
Полученное значение конвективного коэффициента теплообмена αконв = 70 Вт/м2·ºС на интервале изменения температуры от 25 до 600 °С для типовой углеродистой стали является удовлетворительным [8, 9]. Значение коэффициента теплообмена излучением αизд = 0,66 Вт/м2·ºС4, согласно справочным данным, также является удовлетворительным для стали.
Постановка и решение задачи оптимального по быстродействию управления с ограничением на максимальную температуру детали
Найденные в предыдущем разделе параметры использовались для формулировки задачи оптимального по быстродействию управления. В общем виде для рассматриваемой осесимметричной системы математическая модель процесса сквозного индукционного нагрева может быть представлена в виде уравнений Максвелла и Фурье [8, 9]:
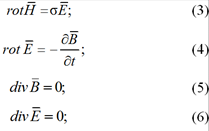
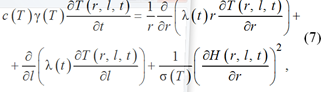
где 
– вектор напряженности магнитного поля; σ – электропроводность; – вектор напряженности электрического поля;
– вектор плотности магнитного потока; t – время; T – температура; с(Т) – удельная теплоемкость; γ(Т) – плотность; λ(t) – коэффициент теплопроводности; r – радиальная координата; l – продольная координата; 
L – длина; R – радиус; tк – время окончания нагрева, с краевыми условиями
(8)
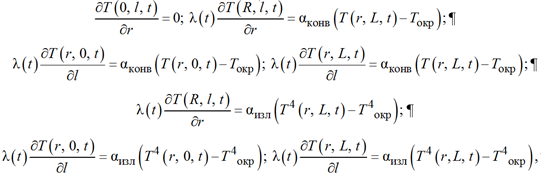
где Т0 – начальная температура; Токр – температура окружающей среды.
В качестве управляющего воздействия рассматривается сосредоточенное управляющее воздействие по напряжению на источнике питания u(t).
На управляющее воздействие накладывается ограничение в следующем виде:
(9)
Согласно требованиям, предъявляемым к технологическим процессам нагрева перед дальнейшей обработкой металла давлением, температура в конце процесса для стальных заготовок должна составлять 1 200 °C с температурным перепадом между центром и поверхностью заготовки не более ±50 °С [1, 2]. Контроль конечной температуры производится вдоль центрального поперечного сечения нагреваемой заготовки. Тогда требование к конечному состоянию для данной двумерной задачи может быть записано в форме
(10)
где l2 = 47,5 мм – середина продольного сечения детали; требуемая температура Tк = 1 200 °С; ε0 – максимальное отклонение температуры от заданного значения.
В производственных рамках, как правило, индукционный нагрев является лишь частью целого технологического процесса. Например, как отмечалось ранее, данный вид нагрева широко используется в технологических комплексах пластической деформации, в так называемых комплексах «печь – пресс».
Одним из важных показателей, характеризующих производственный процесс, является производительность. Поскольку производительность индукционного нагревателя влияет на производительность всего технологического процесса, в качестве критерия оптимальности может выступать критерий быстродействия:
(11)
В ряде случаев из-за интенсивного нагрева с высокой мощностью, характерного для процессов сквозного индукционного нагрева, на поверхности детали могут наблюдаться значительные превышения предельно допустимых значений температуры, обусловленных физической природой процесса.
В этих случаях задача оптимального управления формулируется с учетом фазового ограничения на максимальную температуру поверхности заготовки, которое записывается в следующем виде:
(12)
где Тдоп – максимально допустимая температура нагрева.
Таким образом, рассматриваемая задача оптимального управления состоит в определении сосредоточенного управляющего воздействия u(t), стесненного ограничением (9), которое бы обеспечивало перевод объекта (3)–(7) из заданного начального состояния (8) в требуемое конечное (10) с минимальным значением критерия оптимальности (11)
с учетом фазового ограничения на максимальную температуру (12).
Решение сформулированной задачи было получено с помощью альтернансного метода. Согласно нему доказано, что оптимальное управление по критерию быстродействия представляет собой релейную функцию времени, попеременно принимающую свои предельно допустимые, согласно (9), значения. Причем количество интервалов постоянства однозначно определяет число точек с максимальным отклонением температуры по радиальному сечению детали от требуемого значения. Однако, как указано в [10], подобный характер управления не обеспечивает выполнения фазового ограничения (12). Для обеспечения его выполнения в программу управления включают особый интервал движения по ограничению, после чего управляющее воздействие принимает следующий вид:
(13)
где umax – предельно допустимое значение напряжения; uT(t) – управляющее воздействие на участке стабилизации (участке движения по ограничению); N – число интервалов управления; Δj – длительности интервалов постоянства управляющего воздействия; t1 – время выхода на ограничение.
Как указано в [8–10], как правило, максимальные отклонения температуры 
, соответствующие двум и трем интервалам постоянства управляющего воздействия, удовлетворяют технологическим требованиям сквозного индукционного нагрева, без существенного роста точности при дальнейшем увеличении количества интервалов.
В связи с этим сформулированная задача решается для случая 
. Тогда выражение (13) может быть переписано в виде
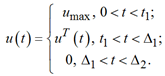
Если длительность стадии нагрева заготовки существенна, вид управляющего воздействия на участке движения по ограничению представляет собой кусочно-постоянную функцию времени (рис. 4).
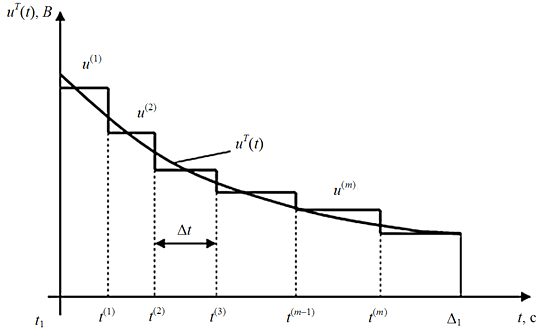
Рис. 4. Аппроксимация управляющего воздействия uT(t) на участке движения по ограничению:
Δt – величина шага по времени; u(m) – напряжение на m-м временном шаге; t(m) – m-й момент времени;
Δ1 – длительность участка движения по ограничению
Fig. 4. Approximation of control action uT(t) on the restricted traffic section:
Δt – time step value; u(m) – voltage on m-th time step; t(m) – m-th time step; Δ1 – duration of holding stage
Подобная аппроксимация управляющего воздействия uT(t) на участке движения по ограничению сводится к итерационной процедуре поиска на каждом шаге ∆t такого значения напряжения u(m), 
, которое бы обеспечивало равенство Tmax(t) = Tдоп в моменты времени t(1), t(2), ..., t(m), где t(m) = t1 + m · ∆t.
Указанному значению 
согласно теории альтернансного метода, соответствует температурное распределение по радиальному сечению детали, имеющее 3 точки 
с максимальным отклонением температуры от требуемой (рис. 5).
Рис. 5. Форма кривой температурного распределения для отклонения
Fig. 5. The shape of the temperature distribution curve for deviation
Система уравнений, соответствующая указанной кривой, записывается в следующем виде [11, 12]:
(14)
где 
– координаты точек с максимальным отклонением температуры от требуемого значения; – коэффициент, задающий порядок знакочередования отклонений.
В результате численного расчета двумерной FLUX-модели было получено результирующее температурное распределение по радиусу цилиндрической заготовки T(r, l2, t) (рис. 6), являющееся решением системы уравнений (14).
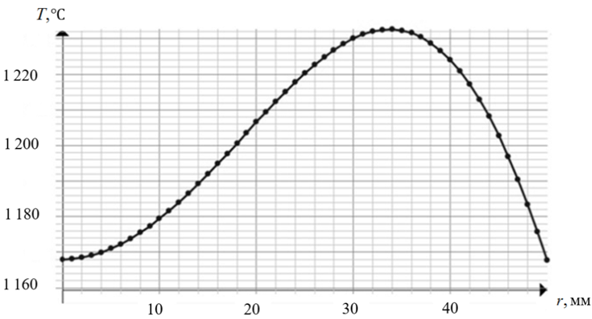
Рис. 6. Результирующее распределение температуры по радиальному сечению заготовки
Fig. 6. Final temperature distribution along the radial cross-section of the workpiece
Результаты решения задачи оптимального по критерию быстродействия с учетом технологичес-
кого ограничения представлены в табл. 3.
Таблица 3
Table 3
Результаты решения задачи оптимального быстродействия с учетом технологического ограничения
Results of solving the optimal performance problem taking into account technological limitations
|
Параметр |
Значение |
|
Максимальное температурное отклонение |
32 |
|
Длительность t1 участка нагрева при максимальном напряжении umax, с |
39,2 |
|
Момент окончания участка движения по ограничению ∆1, с |
110,8 |
|
Момент окончания участка выравнивания температуры ∆2, с |
124,1 |
Вид оптимального по быстродействию управления по напряжению на источнике питания индуктора представлен на рис. 7.
Рис. 7. График изменения напряжения в процессе термической обработки заготовки
Fig. 7. Graph of voltage changes during heat treatment of the workpiece
График изменения температуры заготовки в течение всего процесса термической обработки в индукционной нагревательной системе показан на рис. 8.
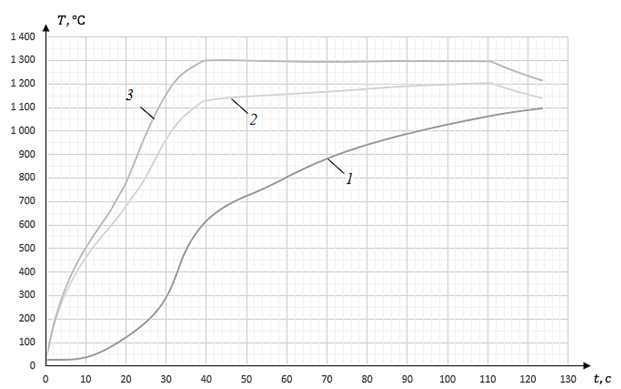
Рис. 8. График изменения температуры заготовки в процессе термической обработки:
1 – температура в центре заготовки; 2 – температура на поверхности заготовки;
3 – максимальная температура заготовки
Fig. 8. Graph of workpiece temperature changing during heat treatment:
1 – temperature of a core; 2 – temperature on the surface; 3 – maximal temperature
Из анализа графика следует, что максимальная температура на всем временном интервале не превышает 1 300 °С, что подтверждает выполнение фазового ограничения (12).
Заключение
В работе рассмотрено применение альтернансного метода для получения полной информации об объекте управления, в качестве которого рассматривается процесс сквозного индукционного нагрева в лабораторной установке. Дальнейшее решение задачи оптимального управления по напряжению источника питания позволило повысить производительность рассматриваемого процесса за счет сокращения времени нагрева в условиях отсутствия локальных перегревов по радиальному сечению детали.
1. Dossett J., Totten G. E. ASM Handbook, Volume 4A: Steel Heat Treating Fundamentals and Processes. ASM International, 2013. 778 p.
2. Rudnev V., Loveless D., Cook R. L. Handbook of induction heating. CRC press, 2017. 772 p.
3. Diligenskaia A. N., Rapoport E. Ia. Analiticheskie usloviia optimal'nosti v obratnykh zadachakh teploprovod-nosti [Analytical conditions of optimality in inverse prob-lems of thermal conductivity]. Teplofizika vysokikh temperatur, 2021, vol. 59, no. 3, pp. 401-410.
4. Diligenskaia A. N. Metod minimaksnoi optimizatsii v dvumernoi granichnoi obratnoi zadache teploprovodnosti [Minimax optimization method in two-dimensional boundary inverse problem of thermal conductivity]. Teplofizika vysokikh temperatur, 2019, vol. 57, no. 2, pp. 226-233.
5. Pleshivtseva Y., Pavlushin A., Popov A. Optimal Design of Inductor Coils for Surface Hardening. 2022 International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM). IEEE, 2022. Pp. 680-685.
6. Popov A. Optimization of Heating Stage for Induction Hardening of Cylindrical Billets. 2019 XXI International Conference Complex Systems: Control and Modeling Problems (CSCMP). Samara, 2019. Pp. 237-241.
7. Sharapova O. Iu. Chislennoe modelirovanie protsessa periodicheskogo induktsionnogo nagreva na baze konechno-elementnogo programmnogo paketa FLUX [Numerical simulation of the periodic induction heating process based on the finite element software package FLUX]. Vestnik Samarskogo gosudarstvennogo tekhnicheskogo universiteta. Seriia: Tekhnicheskie nauki, 2011, no. 7 (28), pp. 180-185.
8. Rapoport E. Ia., Pleshivtseva Iu. E. Metody polu-beskonechnoi optimizatsii v prikladnykh zadachakh uprav-leniia sistemami s raspredelennymi parametrami [Methods of semi-infinite optimization in applied control problems of systems with distributed parameters]. Moscow, Nauka Publ., 2021. 286 p.
9. Rapoport E. Ia., Pleshivtseva Iu. E. Optimal'noe upravlenie temperaturnymi rezhimami induktsionnogo nagreva [Optimal control of induction heating temperature conditions]. Moscow, Nauka Publ., 2012. 309 p.
10. Rapoport E. Ia. Al'ternansnyi metod v prikladnykh zadachakh optimizatsii [The alternative method in applied optimization problems]. Moscow, Nauka Publ., 2000. 336 p.
11. Pleshivtseva Y., Popov A., Pavlushin A. New Ap-proach to Optimization of Surface Induction Hardening Process. 2022 4th International Conference on Control Systems, Mathematical Modeling, Automation and Energy Efficiency (SUMMA). IEEE, 2022. Pp. 525-530.
12. Pleshivtseva Y., Popov A., Pavlushin A. Software solution for optimal design of inductor for surface hardening. 2021 3rd International Conference on Control Systems, Mathematical Modeling, Automation and Energy Efficiency (SUMMA). IEEE, 2021. Pp. 646-649.
