graduate student from 01.01.2020 to 01.01.2023
Russian Federation
graduate student
Russian Federation
employee
Russian Federation
The problem of automating the finding of centers of mass for a system of objects on the Earth's surface is considered. This task often arises, for example, in the course of optimizing the logistics network of the company in quickening the order delivery to the customers. Automation of this process contributes to the optimization of the staff involved, improves the quality of decisions on the development of logistics networks by estimating the situation based on data. The authors of the article suggest to use the modified metric K-means machine learning algorithm for determining the optimal locations of distribution centers of the delivery of goods to settlements. Such centers can significantly reduce transportation costs, as well as provide a high level of customer service quality. The research is also touches upon the more complicated cases of using the chosen method for finding warehouse locations, since the process depends on the logistics strategy of the company. The data were analyzed and a set of features suitable for the clustering algorithm as weights was determined. The data were processed and transformed to apply the algorithm. There has been developed a class for finding distances between points on the highways. The optimal number of clusters is calculated. The clustering algorithm has been modified in terms of calculating distances between objects. With the modified algorithm, a set of candidate points for the location of distribution centers was obtained.
data processing, machine learning, Python, K-means algorithm, clustering, elbow method
Введение
В цепочке поставок склады играют роль важного стратегического узла и позволяют компаниям достигать двух целей – сокращать затраты и экономить время. Они консолидируют оптовые поставки в соответствии с конкретными пожеланиями заказчика и устанавливают равновесие между спросом и предложением. Близость склада к клиентской базе является важным аспектом, который определяет скорость доставки. С появлением возможности аналитики больших данных управление цепочками поставок становится более эффективным. Актуальность проблемы продиктована требованиями заказчика-продавца, который заинтересован в данном исследовании. Требование заказчика сформулировано следующим образом: из множества точек на территории страны, площадь которой более 9 000 000 км2, выбрать наиболее подходящие с точки зрения расстояний до магазинов для расположения в них распределительных центров. В качестве фактора, влияющего на выбор города для расположения в нем склада, выступает суммарная прибыль всех магазинов в каждом из городов. Исходя из этих требований, задача исследования была сформулирована как «автоматизация поиска точек-кандидатов для оптимального размещения в них распределительных центров для системы объектов на поверхности Земли с учетом дополнительных параметров, в данном случае – прибыли». Задача будет решаться с помощью алгоритма кластеризации K-средних, модифицированного авторами в части расчета метрики между объектами. Кластеризация – это задача неконтролируемого машинного обучения, т. к. изначально принадлежность объектов кластерам неизвестна, а известны только характеристики объектов, как в случае данной задачи.
Пример решения поставленной задачи и отладка алгоритма будут рассмотрены на наборе данных Superstore Dataset с веб-площадки Kaggle.com, где проводятся соревнования по машинному обучению [1]. Набор данных содержит информацию о заказах магазина и пунктах доставки. Так как в информации о пунктах доставки содержится лишь название страны и города, необходимо будет написать программу для определения координат населенного пункта. Перечень населенных пунктов
в наборе данных относится к одному континенту. Задача будет рассмотрена с учетом доставки грузов автомобилем, следовательно, в качестве метрики логично будет взять расстояние по автодорогам, что является отличительной особенностью алгоритма, предложенного авторами статьи. Такое расстояние может существенно отличаться от евклидова расстояния, которое используется в классическом алгоритме K-средних, ведь дороги могут иметь одностороннее направление, а также изгибы (например, вокруг возвышенностей). Наличие рек и заливов тоже существенно увеличивает расстояние между пунктами ввиду того, что для их пересечения зачастую необходимо проделать долгий путь. Как следствие, некорректно оперировать только евклидовым расстоянием для оптимизации логистических сетей. Преимущество и новизна метода, использованного в исследовании, заключается в том, что он позволяет использовать в качестве метрики расстояние по автомобильным дорогам для пар объектов.
Состояние проблемы
Проблема поиска оптимального расположения распределительных центров рассматривалась и ранее, так, в статье авторов H. Prakash и K. Jayavel [2] предлагается использовать алгоритм DBSCAN для решения задачи нахождения оптимальных точек для расположения складов, однако расстояние по дорогам в качестве метрики не используется. В статье [3] авторы S. Škerlič и R. Mucha решают задачу поиска оптимальных точек для расположения складов с помощью алгоритма иерархической кластеризации и в качестве влияющего на выбор алгоритма фактора справедливо приводят возможность учета множества признаков. Однако для возможности использования альтернативных алгоритмов, в том числе K-средних, с учетом многих признаков можно применить метод главных компонент с целью уменьшения пространства признаков. Таким образом, можно продолжить исследование и учесть множество выбранных признаков.
Цели и задачи исследования
Доступные аналогичные решения и алгоритмы используют ограниченный набор метрик. Если решать задачу оптимизации для доставки, необходимо учитывать реальные расстояния, которые проходит транспорт.
Целью работы является нахождение главных точек (центров кластеров) и минимизация суммарного отклонения точек кластеров от центров их скопления с учетом суммарной прибыли по населенному пункту в качестве весов, нахождение оптимального расположения распределительных центров для обеспечения заказов из ближайших городов и уменьшения затрат на транспортировку.
На данный момент не существует тривиального решения такой задачи ввиду отсутствия программного обеспечения с открытым исходным кодом, учитывающего дополнительные параметры, для поиска оптимального расположения складов. В тех решениях, которые представлены в открытом доступе, не учитываются расчеты расстояний по автодорогам, учитываются лишь те меры, которые есть в классических реализациях алгоритмов кластеризации: евклидово расстояние, расстояние Хэмминга, расстояние Чебышева и т. д.
Для достижения поставленной цели необходимо решить следующие задачи:
1. Провести анализ данных и определить набор признаков, подходящих в качестве весов.
2. Обработать данные, избавиться от аномалий и выбросов, найти пропуски, преобразовать данные к необходимому для алгоритма кластеризации виду.
3. Выбрать алгоритм кластеризации для нахождения главных точек.
4. Найти оптимальное количество кластеров.
5. Реализовать класс на языке программирования Python для нахождения расстояний по автодорогам между двумя и более точками, характеризуемыми долготой и широтой.
6. Разработать класс на языке Python для выбранного алгоритма кластеризации с возможностью учета весов и подачи собственных метрик.
7. Рассчитать главные точки.
Понятие кластеризации и формальная постановка задачи
Кластерный анализ, или кластеризация, – это многомерная статистическая процедура группировки объектов таким образом, чтобы объекты, упорядоченные в однородную группу, были более схожи между собой, чем с объектами из других групп (кластеров). Кластеризацию можно выполнить
с помощью различных алгоритмов, существенное отличие которых – в определении того, что представляет собой кластер, и в эффективности поиска кластеров.
Пусть X – множество объектов – городов, в которых есть магазины, Y – множество меток кластеров – распределительных центров. Заранее определена функция расстояния между объектами 
, в конкретном случае – кратчайшее расстояние между объектами по дорогам, км. Имеется конечный набор объектов для обучения 
, где m – количество объектов. Необходимо разбить множество объектов на непересекающиеся подмножества так, чтобы каждое подмножество состояло из объектов, близких по метрике p, а объекты разных подмножеств существенно отличались. Каждому объекту – городу 
сопоставляется номер кластера yi, т. е. того распределительного центра, из которого город будут получать товар, а алгоритм кластеризации – это функция a: X → Y. Множество Y может быть как заранее известно, так и наоборот. В случае, когда это множество не известно заранее, ставится задача определения оптимального числа кластеров с точки зрения одного из критериев качества кластеризации. Подтверждением того, что кластеризация относится к способу машинного обучения без учителя, т. е. неконтролируемого обучения, является то, что метки исходных объектов yi изначально не известны.
Выбор алгоритма кластеризации для задачи нахождения оптимального расположения распределительных центров
В кластерном анализе метод локтя – это эвристический подход, который используется для определения оптимального количества кластеров
в наборе данных. Метод состоит в построении графика объясненной вариации в зависимости от количества кластеров и выборе «локтя» кривой
в качестве количества используемых кластеров. Алгоритм кластеризации циклически повторяется для 
, где k – количество кластеров, и на каждой итерации отображается на графике сумма квадратов внутрикластерных расстояний до центра кластера (WCSS):
,
где Nc – номер кластера; Ci – кластер; p – функция расстояния; xCi – прогнозируемый центр тяжести кластера.
Квадрат ошибки для каждой точки равен квадрату расстояния от точки до центра кластера, которому точка принадлежит.
Оценка WCSS – это сумма квадратов расстояний для всех кластеров.
Можно использовать любую метрику расстояния, такую как евклидово расстояние, расстояние Чебышева или расстояние по автодорогам в случае поставленной задачи.
График оценки WCSS представлен на рис. 1.
В данном случае на графике виден «локоть», отображающий значение количества кластеров по оси X, по достижении которого дальнейшая кластеризация не приносит значительного сокращения суммы квадратов внутрикластерных расстояний по оси Y.
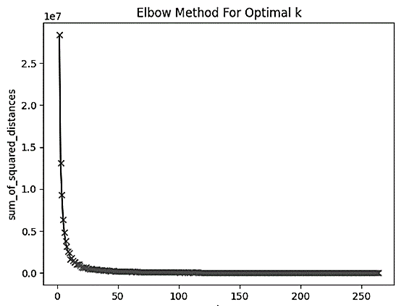
Рис. 1. График оценки WCSS
Fig. 1. Diagram of WCSS Evaluation
Алгоритм кластеризации K-средних
Для достижения поставленной цели исследования было принято решение модифицировать один из существующих алгоритмов кластеризации в части расчета метрик между объектами. В качестве метрики вместо евклидова расстояния будет использоваться кратчайшее расстояние по автомобильным дорогам, км. Подойдет любой метрический алгоритм, т. е. алгоритм, одним из этапов которого будет расчет расстояний между объектами. Одним из таких алгоритмов является K-средних [4].
Основная идея метода заключается в цикличном повторении двух этапов:
– распределить объекты выборки по кластерам;
– пересчитать центры кластеров.
Для тестирования работы алгоритма были сгенерированы объекты в декартовой системе координат в диапазоне [–3; 4] по X и [0; 6] по Y. В начале работы алгоритма K-средних центры кластеров выбираются случайно в пространстве признаков (рис. 2).
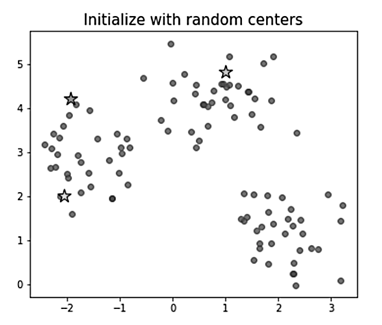
Рис. 2. Инициализация случайных центров
Fig. 2. Initialization of random centers
Каждый объект пространства относится к тому кластеру (центру тяжести), к которому объект оказался наиболее близко (рис. 3).
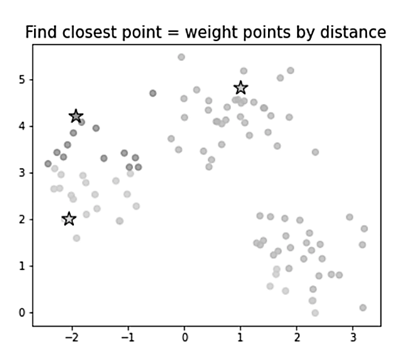
Рис. 3. Отнесение объектов к ближайшему кластеру
Fig. 3. Assigning objects to the nearest cluster
На следующем шаге необходимо пересчитать центры кластеров как среднее арифметическое векторов признаков всех объектов, вошедших в данный кластер (пересчет центра масс) (рис. 4).
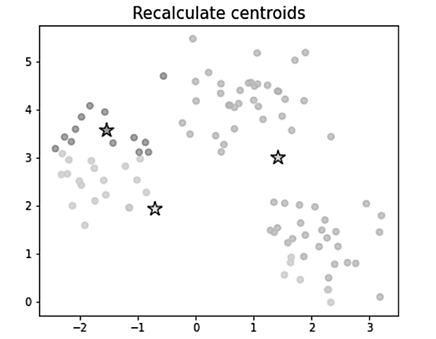
Рис. 4. Пересчет центров кластеров
Fig. 4. Recalculation of cluster centers
После обновления центров объекты снова перераспределяются в кластеры. Далее вновь уточняется положение центров. Процесс необходимо продолжать до тех пор, пока центры кластеров не перестанут изменяться. Итоговые кластеры представлены на рис. 5.
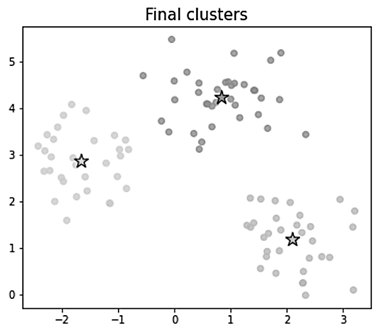
Рис. 5. Итоговые кластеры
Fig. 5. Resulting clusters
Среди достоинств данного метода можно выделить следующие:
– возможность учитывать веса, что достаточно важно для достижения поставленной цели;
– для алгоритма K-средних можно задать положение начальных центров кластеров при инициализации.
Но есть также и недостатки, в основном касающиеся выбора начального приближения:
– при выборе положения начальных центров существует вероятность попасть в область пространства признаков, где нет точек выборки. В качестве решения можно объявить некоторые объекты выборки начальными центрами кластеров;
– если кластеры размещены кучно, их начальное положение с большой вероятностью может оказаться далеким от итогового положения центров кластеров. Пример такой ситуации представлен на рис. 6.
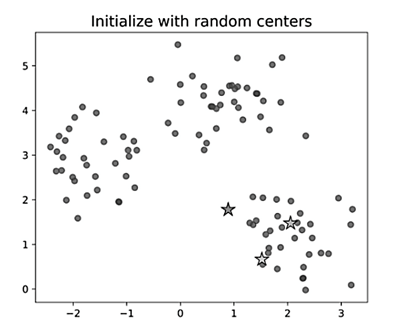
Рис. 6. Инициализация центров в скоплении объектов
Fig. 6. Initialization of centers in a cluster of objects
Следствием такой ситуации может быть некорректная итоговая кластеризация (рис. 7).
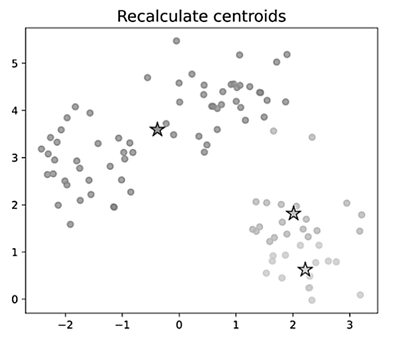
Рис. 7. Некорректная итоговая кластеризация
Fig. 7. Resulting incorrect clustering
Учитывая вышесказанное, можно сделать вывод: случайная инициализация центров кластеров может негативно отразиться на результате.
Оба этапа K-средних по умолчанию работают на уменьшение среднего квадрата евклидова расстояния от объектов до центров их кластеров:
,
где Ф0 – средний квадрат евклидова расстояния от объектов до центров их кластеров; n – количество объектов; K – количество кластеров; k – текущий кластер; μk – центр текущего кластера; xi – текущий объект.
На этапе отнесения объектов к кластеру выбирается ближайший центр масс, т. е. минимизируется каждое слагаемое в Ф0 . На следующем этапе, в котором пересчитываются центры масс, выбирается центр таким образом, чтобы при фиксированном наборе объектов, отнесенных к кластеру, для всех k минимизировать выражение, стоящее под суммой по K:
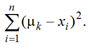
Тут становится принципиально, что квадрат расстояния определяется как квадрат разности векторов, т. к. отсюда при дифференцировании по μk и записи необходимого условия экстремума получается, что центры кластеров необходимо пересчитывать как среднее арифметическое по xi , принадлежащих кластеру [4].
Вышесказанное не гарантирует нахождения минимума Ф0. Нет гарантии и нахождения глобального минимума. Можно лишь доказать, что процесс сойдется в один из локальных минимумов.
Алгоритм позволяет задать положение начальных центров, их количество, а также определить центры как максимально удаленные друг от друга точки. Более того, алгоритм позволяет учитывать дополнительные характеристики объектов (в данном случае прибыль по городам) в качестве весов, что также выделяет его как подходящий. И самой значимой особенностью, повлиявшей на выбор алгоритма K-средних, является использование метрики для расчета расстояний между объектами. Учитывая это, можно с уверенностью сказать, что алгоритм применим для решения поставленной задачи.
Алгоритм нахождения оптимального расположения распределительных центров для доставки заказов и его реализация
Для нахождения оптимальных центров распределения заказов, взвешенных по суммарной прибыли, были решены все поставленные задачи, а именно: проведен анализ набора данных и определен набор весовых признаков, произведена обработка данных, выбран алгоритм кластеризации, реализован класс для нахождения расстояний между объектами по автомобильным дорогам, модифицирован алгоритм кластеризации K-средних, где в качестве метрики используется расстояние по автомобильным дорогам, найдены главные точки. Ниже изложено более подробное описание исследования. Блок-схема алгоритма нахождения оптимального расположения распределительных центров для доставки заказов представлена на рис. 8.
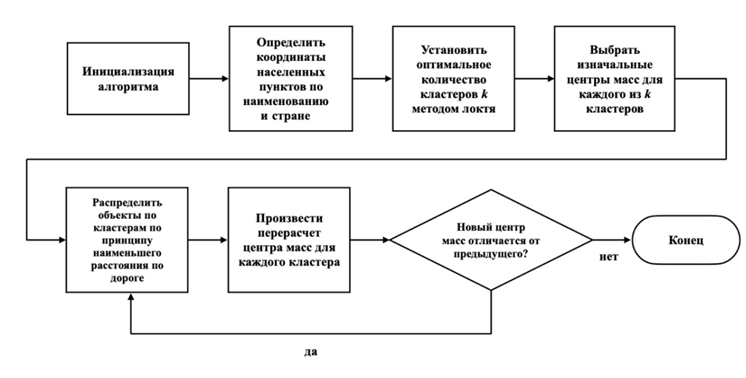
Рис. 8. Блок-схема алгоритма нахождения оптимального расположения
распределительных центров для доставки заказов
Fig. 8. Graph of the algorithm of finding the optimal location
distribution centers for order delivery
Изначально известны только наименования населенных пунктов и страны, в которых они находятся. После инициализации алгоритма поиска оптимального расположения складов рассчитываются координаты населенных пунктов. Вычисляется оптимальное количество кластеров с помощью метода локтя. Полученное число передается в алгоритм K-средних и выбираются случайные центры масс для каждого кластера. Объекты – города распределяются по кластерам по принципу наименьшего расстояния по дорогам. Расчет расстояний обеспечивает класс DistancesFinder. Производится пересчет центра масс для каждого кластера как среднее арифметическое векторов характеристик всех вошедших в этот кластер объектов. Если новый центр масс отличается от предыдущего, алгоритм поиска оптимального распределения складов возвращается к блоку распределения объектов по кластерам, иначе алгоритм завершает работу. Далее будут детально описаны функции и классы, отвечающие за работу каждого из блоков.
После загрузки открытого набора данных superstore dataset по заказам магазина была проведена первичная обработка с целью приведения к формату табличных данных, используемому в языке программирования Python, pandas DataFrame. Далее были исследованы и отобраны признаки, подходящие для применения алгоритмов кластеризации, а именно – количественные. Из всего массива были выделены следующие характеристики:
– код города;
– сумма продажи;
– количество товара в заказе;
– сумма скидки;
– прибыль.
Для эксперимента в качестве веса был выбран признак «Прибыль». Таким образом, город, в котором достигается наибольшая прибыль, будет иметь больший вес для размещения рядом с ним распределительного центра. Из расчетов были исключены значения с прибылью меньше 0.
Для применения алгоритма необходимо знать координаты пунктов доставки, характеризующиеся долготой и широтой. В представленном наборе данных из характеристик пунктов доступны только страна и город. Получить координаты населенных пунктов позволяет открытая библиотека, написанная на языке программирования Python, geopy [5]. Далее для определения расстояний по автомобильным дорогам был реализован класс на языке Python – DistancesFinder. Для расчета расстояний используется Open Source Routing Machine – маршрутизатор с открытым исходным кодом [6]. Эта библиотека позволяет получить кратчайший путь по дорожным сетям и реализована на языке программирования C++, что говорит в пользу ее производительности.
Внутри класса были разработаны следующие методы:
1) _validate_coord_value – проверка значений поданных координат, долгота в диапазоне [–180; 180], широта в диапазоне [–90; 90];
2) _check_coords – проверка на тип входящих координат;
3) _create_url_for_req – сборка ссылки для get запроса к API Open Source Routing Machine;
4) _get_routes_by_car – отправить get запрос
к API Open Source Routing Machine;
5) _get_shortest_route_dist – получить общую дистанцию для маршрута между n пунктами, где n ≥ 2;
6) get_shortest_dist_by_car – основной метод, исполняющий все вышеуказанные методы и возвращающий расстояние маршрута, км.
В качестве алгоритма кластеризации был выбран метрический алгоритм K-средних, описание, достоинства и недостатки которого были изложены ранее. Чтобы не писать весь алгоритм K-средних заново, была взята его существующая реализация на языке программирования Python из бесплатной открытой библиотеки программного обеспечения для машинного обучения scikit-learn [7]. Алгоритм был модифицирован авторами статьи в соответствии с лицензией библиотеки в части определения расстояний. Вместо функции расчета евклидова расстояния между центрами кластеров и объектами был применен метод get_shortest_dist_by_car из разработанного класса DistancesFinder. Подробнее с модификацией алгоритма можно ознакомиться в открытом репозитории [8] авторов статьи.
Далее необходимо определить оптимальное количество кластеров для всех существующих пунктов доставок с учетом их прибыли в качестве весов с использованием модифицированного алгоритма K-средних. Для этого был применен описанный выше метод локтя, который показал, что по достижении 11 кластеров дальнейшая кластеризация не дает существенного сокращения суммы квадратов расстояний.
Последним этапом была произведена взвешенная кластеризация с использованием модифицированного алгоритма K-средних и последующей визуализацией кластеров с использованием библиотеки matplotlib [9].
Для наглядного отображения результатов была реализована функция отображения на карте центров кластеров, пунктов доставок заказов, а также их связей. Для визуализации была использована библиотека отображения данных на карте folium [10]. Отображение центров масс, пунктов доставок заказов и их связей на карте представлено на рис. 9.
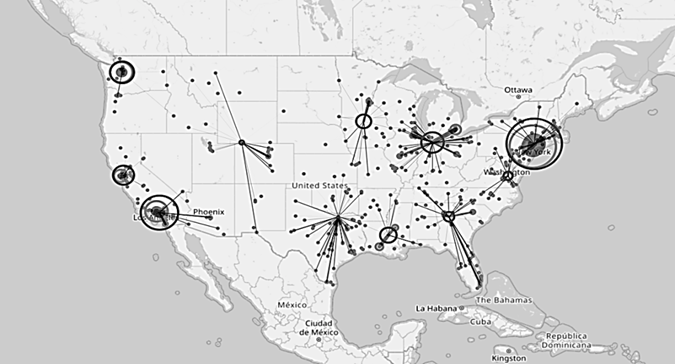
Рис. 9. Отображение пунктов доставок и центров кластеров на карте
Fig. 9. Displaying delivery points and cluster centers on the map
Радиусы точек пунктов доставок и центров кластеров пропорциональны их прибыли. Светло-серые точки на карте – это пункты доставок, а темно-серые – центры кластеров, которые вполне можно объявить кандидатами на пункты распределения товаров. Толщина линий связей также пропорциональна прибыли по населенным пунктам. Можно заметить, что пункты доставок, имеющие наибольшую суммарную прибыль, «перетягивают» к себе центры кластеров, что в целом рационально. С полным исходным кодом проекта можно ознакомиться в открытом репозитории [8] авторов статьи.
Заключение
В результате исследования и применения разработанного алгоритма были найдены точки-кандидаты для оптимального размещения распределительных центров. Для их нахождения были использованы метод локтя – для нахождения оптимального количества кластеров, алгоритм кластеризации K-средних с модификацией в части функции расстояния между объектами – для нахождения центров масс объектов. Также были реализованы сами функции расстояний по автомобильным дорогам для сложных маршрутов. В качестве продолжения исследования можно попробовать использовать в модели дополнительные характеристики объектов – городов, например объемы оборота товаров, с последующим уменьшением размерности пространства характеристик. Также возможно продолжить исследование с использованием других метрических алгоритмов кластеризации или рассмотреть альтернативные подходы к решению задачи.
1. Superstore Dataset // Kaggle. URL: https://www.kaggle.com/datasets/vivek468/superstore-dataset-final (data obrascheniya: 27.02.2023).
2. Prakash H., Jayavel K. An Ensemble Address Clustering Model Towards Warehouse Location Determination // Researchgate. URL: https://www.researchgate.net/publication/352901634_An_Ensem-ble_Address_Clustering_Model_Towards_Warehouse_Location_Determination (data obrascheniya: 27.02.2023).
3. Škerlič S., Mucha R. Identifying warehouse location using hierarchical clustering // Transport Problems. 2016. V. 11, no. 3. P. 121-129.
4. Kantor V. Klasterizaciya // Uchebnik po mashinnomu obucheniyu. URL: https://academy.yandex.ru/handbook/ml/article/klasterizaciya (data obrascheniya: 27.02.2023).
5. GeoPy. URL: https://geopy.readthedocs.io/en/latest/ (data obrascheniya: 27.02.2023).
6. OSRM (Open Source Routing Machine) Documenta-tion. URL: http://project-osrm.org/docs/v5.24.0/api/# (data obrascheniya: 27.02.2023).
7. Clustering // Scikit-learn. URL: https://scikit-learn.org/stable/modules/clustering.html (data obrascheniya: 27.02.2023).
8. Search_centriods: ishodnyy kod proekta stat'i v repozitorii GitHub // GitHub. URL: https://github.com/hwpy/search_centriods (data obrascheniya: 27.02.2023).
9. Matplotlib 3.1.7 documentation. URL: https://matplotlib.org/stable/index.html (data obrascheniya: 27.02.2023).
10. Folium. Python data, leaflet.js maps. URL: https://python-visualization.github.io/folium (data obrascheniya: 27.02.2023).
