Russian Federation
Sevastopol, Russian Federation
Russian Federation
Determining the parameters of the elements of the ship electric power system in the limiting operation mode is carried out by constructing the boundaries of the system stability areas. To improve the efficiency of calculations of limiting modes, it is necessary to create mathematical models and methods that fully take account of the spe-cifics of equations that describe steady-state modes. There is proposed an improved D-partitioning method designed to select parameters that ensure stable parallel operation of the generators. The traditional method of D-partitioning is based on the assumption that usually the desired sets are a union of regions. In particular, this is the case for the linear systems with linear dependence on parameters. In this case, a problem of constructing the stability area can be reduced to a problem of determining the boundary of each area and indicating on which side of the boundary the points of the desired area lie. The main drawback of the D-partitioning method in the traditional formulation is that the range of values is obtained for both real and complex values of the variable parameter. There are considered the equations defining the D-partition curve for the case of linear dependence on one parameter of the coefficients of the characteristic polynomial. For the numerical solution of these equations there is proposed a method that, unlike the known methods, does not require cumbersome and poorly conditioned transformations of the characteristic polynomial.
automatic control system, ship electric power system, generator, real root, stability limits, D-partitioning method, system stability
Введение
Метод D-разбиения широко используется для построения областей устойчивости в пространстве варьируемых параметров различных систем автоматического управления [1–3].
Реализация метода D-разбиения обычно осуществляется на основе графоаналитических процедур, основным недостатком которых является отсутствие гарантированного результата. От этого недостатка свободна реализация метода D-разбиения, основанная на численном решении уравнений, определяющих границы областей устойчивости [4–6].
В работе предлагается способ численного решения уравнений D-разбиения по одному параметру.
Постановка задачи
Рассматривается характеристический многочлен системы автоматического управления с линейной зависимостью коэффициентов от варьируемого скалярного параметра λ Î R
(1)
Кривая D-разбиения определяется уравнением
a(jω, λ) = 0,
где:
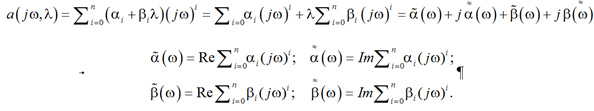(3)
С учетом (3) уравнение (2) можно переписать в виде
(4)
В работе рассматривается численный способ определения вещественных корней уравнения (4).
Уравнение (4) эквивалентно системе уравнений
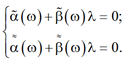(5)
Для решения системы (5) могут быть рассмотрены случаи:
1. Выполняется условие
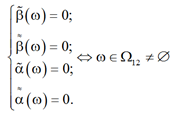(6)
В этом случае "λ Î R
2. Условие (6) не выполняется, т. е. ¢W = Æ.
При невыполнении условий (6) следует рассматривать следующие случаи:
2.1.
(7)
В этом случае
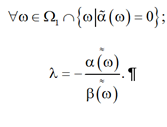
2.2.
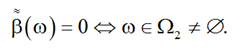(8)
В этом случае
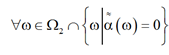
2.3. "ω Î W1 È W2
системе
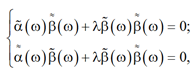
следствием из которой является уравнение
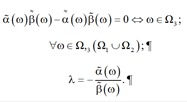(9)
Таким образом, при линейной зависимости от параметра λ
в определении вещественных корней полиномиальных уравнений (6)–(9).
Актуальность проблемы
В настоящий момент актуальной задачей является обеспечение устойчивой параллельной работы генераторных агрегатов судовой электроэнергетической системы.
Существует ряд методов определения устойчивости систем, одним из которых является метод поиска вещественных корней полиномиальных уравнений [7–10], наиболее известными из которых является метод Декарта; метод, основанный на применении теоремы Роля; и метод, основанный на применении полиномов Штурма. В работе предлагается метод определения вещественных корней полиномов, не требующий громоздких и часто плохо обусловленных преобразований многочленов, как этого требуют вышеперечисленные методы.
Материалы исследования
Рассматривается задача вычисления вещественных корней многочлена
(10)
на промежутке x Î [a, b], 0 £ a < b.
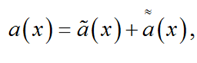
где
Тогда 
возрастает на любом промежутке [a¢, b¢] Ì [a, b],
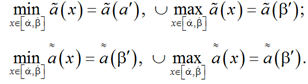
Для нахождения вещественных корней многочлена (10) на промежутке
Если
(11)
то на промежутке [a, b] 
Если условие (11) не выполняется, то проверяем выполнение условий
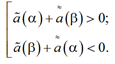(12)
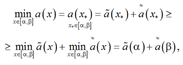(13)
и из неравенств (12), (13) следует
(14)
Неравенство (14) означает, что многочлен
Пусть выполняется второе из неравенств совокупности (12). Тогда
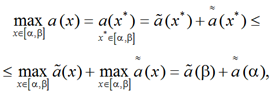(15)
и из неравенств (12), (15) следует
(16)
Неравенство (16) означает, что многочлен а(х)
В случае если на промежутке [a, b]
Доказательство проведем методом от противного. Пусть на каждом 
, для каждого из которых не выполняется неравенство (12). Поскольку длины промежутков уменьшаются в два раза при каждом увеличении 
(17)
Рассмотрим последовательность 
ε-окрестностей точки γ0
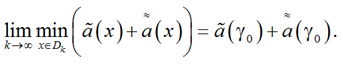(18)
Из (17) и (18) следует:
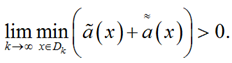(19)
Из (19) следует, что существует окрестность D0
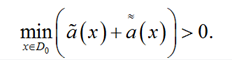(20)
Неравенство (20) справедливо для любого подмножества D͂0
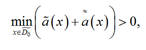(21)
поскольку для подмножества наименьшее значение может только возрасти. Поскольку точка γ0
. Обозначим один из таких отрезков 
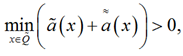(22)
и в то же время поскольку 
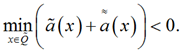(23)
Противоречие соотношений (22) и (23) доказывает утверждение о том, что за конечное число шагов предлагаемый метод позволяет вычислить все вещественные корни многочлена
Заключение
Предлагаемый усовершенствованный метод D-разбиения предназначен для выбора параметров, обеспечивающих устойчивость системы.
Традиционный метод D-разбиения основан на предположении о том, что обычно искомые множества 
представляют собой объединение областей 
. В частности, это имеет место для линейных систем с линейной зависимостью от параметров. В этом случае задача построения областей устойчивости может быть сведена к задаче определения границы Гik каждой из областей 
и указания, с какой стороны от границы лежат точки искомой области.
Данный метод D-разбиения заключается в том, что записываются и решаются уравнения, определяющие объединение границ 
областей 
, таких как 
, где z(λ) – число нулей характеристического полинома справа от мнимой оси, соответствующего параметру λ.
Поиск множества Λi происходит с помощью правил штриховки границ и перебора множеств 
. В искомые множества Λi входят те множества 
, для которых λ = 0. Проверка последнего условия производится для одного из элементов множеств 
Полученные уравнения определяют параметры элементов системы, при которых обеспечивается устойчивость параллельной работы судовых генераторных агрегатов. В свою очередь, предложенный метод позволяет прогнозировать возникновение аварийных ситуаций в судовой электроэнергетической системе.
1. Gryazina E. N., Polyak B. T., Tremba A. A. Sovremennoe sostoyanie metoda D-razbieniya // Avtomatika i telemehanika. 2008. № 12. S. 3-40.
2. Venikov V. A., Litkens I. V. Matematicheskie osnovy teorii avtomaticheskogo upravleniya rezhimami elektrosistem. M.: Vyssh. shk., 1989. 197 s.
3. Kuncevich V. M. Upravlenie v usloviyah neopredelennosti: garantirovannye rezul'taty v zadachah upravleniya i identifikacii. Kiev: Naukova dumka, 2006. 264 s.
4. Dorf R., Bishop R. Sovremennye sistemy upravleniya / per. s angl. B. I. Kopylova. M: Laboratoriya bazovyh znaniy, 2002. 832 s.
5. Antonov V. N., Terehov V. A., Tyukin I. Yu. Adaptivnoe upravlenie v tehnicheskih sistemah. SPb.: Izd-vo Sankt-Peterburg. un-ta, 2001. 244 s.
6. Krasnodubec L. A. Terminal'noe upravlenie v morskih nablyudatel'nyh sistemah s podvizhnymi platformami sbora dannyh // Izv. RAN. Teoriya i sistemy upravleniya. 2008. № 2. S. 141-153.
7. Koneva S. A., Caloev V. M. Issledovanie avariynogo perehodnogo processa v generatornom agregate sudovoy elektrostancii // Journal of Advanced Research in Technical Science. 2019. Iss. 17. V. 2. P. 134-138.
8. Barabanov A. T., Koneva S. A. Zadacha analiza ustoychivosti sistemy avtomaticheskogo regulirovaniya konvektivnogo teploobmena // Dinam. sistemy. 2004. Vyp. 18. S. 14-22.
9. Koneva S. A. Analiz tochnosti sistemy upravleniya s raspredelennymi parametrami pri determinirovannyh vozmuscheniyah // Fundamental. i priklad. problemy tehniki i tehnologii. 2018. № 3. S. 23-28.
10. Koneva S. A., Caloev V. M. Analiz kachestva si-stemy avtomaticheskogo regulirovaniya processa konvektivnogo teploobmena // Modernizaciya i innovacionnoe razvitie toplivno-energeticheskogo kompleksa: materialy Mezhdunar. nauch.-prakt. konf. (Sankt-Peterburg, 07-08 oktyabrya 2021 g.). SPb.: NIC «Mashinostroenie», 2021. S. 28-33.
