Россия
Севастополь, Россия
Россия
Определение параметров элементов судовой электроэнергетической системы при предельном режиме работы осуществляется построением границ областей устойчивости системы. Для повышения эффек-тивности расчетов предельных режимов требуется создание математических моделей и методов, достаточно полно учитывающих специфику уравнений, описывающих установившиеся режимы. Предлагается усовершенствованный метод D-разбиения, предназначенный для выбора параметров, обеспечивающих устойчивую параллельную работу генераторных агрегатов. Традиционный метод D-разбиения основан на предположении о том, что обычно искомые множества представляют собой объединение областей. В частности, это имеет место для линейных систем с линейной зависимостью от параметров. В этом случае задача построения областей устойчивости может быть сведена к задаче определения границы каждой из областей и указания, с какой стороны от границы лежат точки искомой области. Основным недостатком метода D-разбиения в традиционной постановке является то, что область значений получена как для вещественных, так и для комплексных значений варьируемого параметра. Рассмотрены уравнения, определяющие кривую D-разбиения для случая линейной зависимости от одного параметра коэффициентов характеристического многочлена. Для численного решения этих уравнений предложен метод, не требующий (в отличие от известных методов) громоздких и плохо обусловленных преобразований характеристического многочлена.
система автоматического управления, судовая электроэнергетическая система, генераторный агрегат, вещественный корень, границы устойчивости, метод D-разбиения, устойчивость системы
Введение
Метод D-разбиения широко используется для построения областей устойчивости в пространстве варьируемых параметров различных систем автоматического управления [1–3].
Реализация метода D-разбиения обычно осуществляется на основе графоаналитических процедур, основным недостатком которых является отсутствие гарантированного результата. От этого недостатка свободна реализация метода D-разбиения, основанная на численном решении уравнений, определяющих границы областей устойчивости [4–6].
В работе предлагается способ численного решения уравнений D-разбиения по одному параметру.
Постановка задачи
Рассматривается характеристический многочлен системы автоматического управления с линейной зависимостью коэффициентов от варьируемого скалярного параметра λ Î R
(1)
Кривая D-разбиения определяется уравнением
a(jω, λ) = 0,
где:
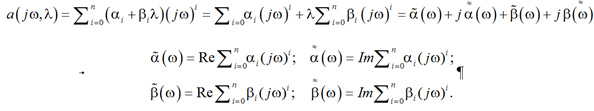(3)
С учетом (3) уравнение (2) можно переписать в виде
(4)
В работе рассматривается численный способ определения вещественных корней уравнения (4).
Уравнение (4) эквивалентно системе уравнений
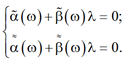(5)
Для решения системы (5) могут быть рассмотрены случаи:
1. Выполняется условие
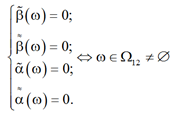(6)
В этом случае "λ Î R
2. Условие (6) не выполняется, т. е. ¢W = Æ.
При невыполнении условий (6) следует рассматривать следующие случаи:
2.1.
(7)
В этом случае
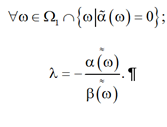
2.2.
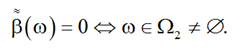(8)
В этом случае
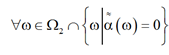
2.3. "ω Î W1 È W2
системе
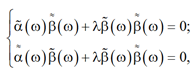
следствием из которой является уравнение
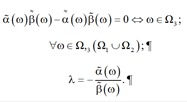(9)
Таким образом, при линейной зависимости от параметра λ
в определении вещественных корней полиномиальных уравнений (6)–(9).
Актуальность проблемы
В настоящий момент актуальной задачей является обеспечение устойчивой параллельной работы генераторных агрегатов судовой электроэнергетической системы.
Существует ряд методов определения устойчивости систем, одним из которых является метод поиска вещественных корней полиномиальных уравнений [7–10], наиболее известными из которых является метод Декарта; метод, основанный на применении теоремы Роля; и метод, основанный на применении полиномов Штурма. В работе предлагается метод определения вещественных корней полиномов, не требующий громоздких и часто плохо обусловленных преобразований многочленов, как этого требуют вышеперечисленные методы.
Материалы исследования
Рассматривается задача вычисления вещественных корней многочлена
(10)
на промежутке x Î [a, b], 0 £ a < b.
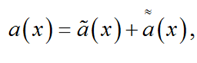
где
Тогда 
возрастает на любом промежутке [a¢, b¢] Ì [a, b],
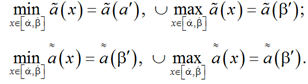
Для нахождения вещественных корней многочлена (10) на промежутке
Если
(11)
то на промежутке [a, b] 
Если условие (11) не выполняется, то проверяем выполнение условий
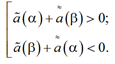(12)
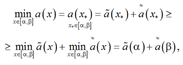(13)
и из неравенств (12), (13) следует
(14)
Неравенство (14) означает, что многочлен
Пусть выполняется второе из неравенств совокупности (12). Тогда
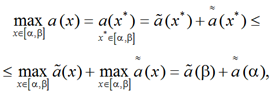(15)
и из неравенств (12), (15) следует
(16)
Неравенство (16) означает, что многочлен а(х)
В случае если на промежутке [a, b]
Доказательство проведем методом от противного. Пусть на каждом 
, для каждого из которых не выполняется неравенство (12). Поскольку длины промежутков уменьшаются в два раза при каждом увеличении 
(17)
Рассмотрим последовательность 
ε-окрестностей точки γ0
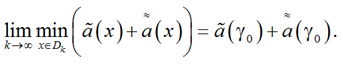(18)
Из (17) и (18) следует:
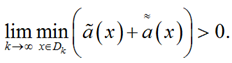(19)
Из (19) следует, что существует окрестность D0
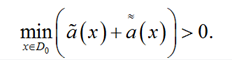(20)
Неравенство (20) справедливо для любого подмножества D͂0
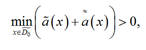(21)
поскольку для подмножества наименьшее значение может только возрасти. Поскольку точка γ0
. Обозначим один из таких отрезков 
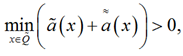(22)
и в то же время поскольку 
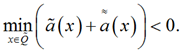(23)
Противоречие соотношений (22) и (23) доказывает утверждение о том, что за конечное число шагов предлагаемый метод позволяет вычислить все вещественные корни многочлена
Заключение
Предлагаемый усовершенствованный метод D-разбиения предназначен для выбора параметров, обеспечивающих устойчивость системы.
Традиционный метод D-разбиения основан на предположении о том, что обычно искомые множества 
представляют собой объединение областей 
. В частности, это имеет место для линейных систем с линейной зависимостью от параметров. В этом случае задача построения областей устойчивости может быть сведена к задаче определения границы Гik каждой из областей 
и указания, с какой стороны от границы лежат точки искомой области.
Данный метод D-разбиения заключается в том, что записываются и решаются уравнения, определяющие объединение границ 
областей 
, таких как 
, где z(λ) – число нулей характеристического полинома справа от мнимой оси, соответствующего параметру λ.
Поиск множества Λi происходит с помощью правил штриховки границ и перебора множеств 
. В искомые множества Λi входят те множества 
, для которых λ = 0. Проверка последнего условия производится для одного из элементов множеств 
Полученные уравнения определяют параметры элементов системы, при которых обеспечивается устойчивость параллельной работы судовых генераторных агрегатов. В свою очередь, предложенный метод позволяет прогнозировать возникновение аварийных ситуаций в судовой электроэнергетической системе.
1. Грязина Е. Н., Поляк Б. Т., Тремба А. А. Современное состояние метода D-разбиения // Автоматика и телемеханика. 2008. № 12. С. 3-40.
2. Веников В. А., Литкенс И. В. Математические основы теории автоматического управления режимами электросистем. М.: Высш. шк., 1989. 197 с.
3. Кунцевич В. М. Управление в условиях неопределенности: гарантированные результаты в задачах управления и идентификации. Киев: Наукова думка, 2006. 264 с.
4. Дорф Р., Бишоп Р. Современные системы управления / пер. с англ. Б. И. Копылова. М: Лаборатория базовых знаний, 2002. 832 с.
5. Антонов В. Н., Терехов В. А., Тюкин И. Ю. Адаптивное управление в технических системах. СПб.: Изд-во Санкт-Петербург. ун-та, 2001. 244 с.
6. Краснодубец Л. А. Терминальное управление в морских наблюдательных системах с подвижными платформами сбора данных // Изв. РАН. Теория и системы управления. 2008. № 2. С. 141-153.
7. Конева С. А., Цалоев В. М. Исследование аварийного переходного процесса в генераторном агрегате судовой электростанции // Journal of Advanced Research in Technical Science. 2019. Iss. 17. V. 2. P. 134-138.
8. Барабанов А. Т., Конева С. А. Задача анализа устойчивости системы автоматического регулирования конвективного теплообмена // Динам. системы. 2004. Вып. 18. С. 14-22.
9. Конева С. А. Анализ точности системы управления с распределенными параметрами при детерминированных возмущениях // Фундаментал. и приклад. проблемы техники и технологии. 2018. № 3. С. 23-28.
10. Конева С. А., Цалоев В. М. Анализ качества си-стемы автоматического регулирования процесса конвективного теплообмена // Модернизация и инновационное развитие топливно-энергетического комплекса: материалы Междунар. науч.-практ. конф. (Санкт-Петербург, 07-08 октября 2021 г.). СПб.: НИЦ «Машиностроение», 2021. С. 28-33.
