Россия
с 01.01.2020 по 01.01.2024
Россия
Россия
Ездовой цикл представляет собой профиль скорости, отражающий особенности эксплуатации транспортного средства. Ездовые циклы используются как на этапе проектирования транспортного средства, так и для проведения натурных испытаний после изготовления прототипов. Алгоритм получения ездового цикла на основе цепей Маркова позволяет синтезировать множество ездовых циклов, удовлетворяющих требуемым параметрам. Процесс синтеза можно рассматривать как сжатие информации с потерями, наличие которых в такого рода практических приложениях не является недостатком. В процессе синтеза одной из ключевых задач является выделение значимых признаков или критериев для набора исходных данных, которые определяют успешность синтеза. При использовании математического аппарата цепей Маркова этап поиска набора оценочных критериев и определения их значений представляет собой отдельную задачу. Синтез набора критериев может производиться на основе целей конкретной практической задачи и существующего набора данных. В процессе синтеза ездового цикла были использованы статистические критерии, такие как средняя скорость, среднее ускорение и замедление и дисперсии этих величин. Алгоритм синтеза ездового цикла на основе цепей Маркова имеет два основных этапа. На первом этапе происходит составление матрицы переходов и подсчет значений статистических критериев, а на втором происходит непосредственно синтез искомой последовательности. Однако такой алгоритм имеет и недостатки, связанные с использованием случайности в процессе синтеза. Распределение отклонений параметров элементов исходного набора данных оказывает существенное влияние на сходимость решения методом цепей Маркова. Анализ распределения отклонений в исходном наборе данных позволяет сделать предположение о вероятности нахождения успешного решения алгоритмом на основе цепей Маркова.
цепи Маркова, синтез ездовых циклов, распределение максимального отклонения параметров, скорость, ускорение, среднеквадратичное отклонение, набор данных
Введение
Ездовые циклы представляют собой профили скорости во времени, используемые для моделирования топливной эффективности [1], расчета количества выбросов вредных веществ двигателями внутреннего сгорания или проектирования электрических трансмиссий [2].
Из ездовых циклов для электромобиля в целом могут быть получены производные испытательные профили для тестирования компонентов электромобиля. Исследователи в работе [3] выявили, что оценки ресурса тяговых аккумуляторных батарей, сделанные с использованием стандартных испытательных профилей тока, и оценка ресурса с использованием профиля тока, синтезированного на основе реальных данных о движении электромобилей, могут отличаться до 38 %. Работа [4] посвящена анализу синтетических и реальных ездовых циклов в части влияния на оценку ресурса тяговых батарей электромобилей, авторами произведено сравнение испытательных циклов, таких как NEDC и DST, реальный ездовой цикл дает большую на 20 % оценку ресурса тяговой батареи.
Исследование [5] посвящено влиянию реальных условий движения на потребление энергии электромобилем. По результатам исследования агрессивное вождение имеет на 16 % более высокое энергопотребление, чем спокойное вождение, а уклоны дороги в пределах 3 % могут изменять потребление энергии до 50 %. Также исследователи приводят оценку влияния температуры окружающей среды, которая при изменении от 20 до 0 ºС может приводить к удвоению потребления энергии электромобилем.
В работе [6] исследователи применяют различные ездовые циклы для проектирования оптимизации электропривода электромобиля.{Citation} Ездовой цикл является сжатым представлением реального профиля вождения автомобиля и генерируется на основе данных, полученных в процессе эксплуатации автомобилей. Существуют ездовые циклы, разработанные для конкретных городов. Такие циклы представляют собой простые профили скорости или имеют дополнительный профиль, отображающий уклон дороги в процессе испытания. Авторы работы [7] разработали ездовой цикл для города Пуна в Индии. Для синтеза использовались отрезки, полученные из записей GPS тестовых автомобилей. Из этих отрезков был сформирован ездовой цикл. В работе [8] исследователи представили результаты синтеза ездового цикла для города Куала (Малайзия), также доступны результаты построения ездовых циклов для Тегерана (Иран) [9]. В работе [10] рассматривается возможность построения ездового цикла с использованием исходных GPS данных, полученных в городе Дубровник (Хорватия) для построения ездового цикла для Иерусалима (Израиль) с применением математического аппарата цепей Маркова. Для синтеза ездовых циклов применяют различные подходы, но наиболее часто используемыми являются алгоритмы на основе цепей Маркова [11] и кластеризации методом k-средних [8]. Так как методы на основе цепей Маркова используют случайность для получения решения, то возможно влияние статистических параметров исходных данных на скорость и результат решения. В работе [12] рассматривается влияние длины цикла на отклонение параметров результата синтеза от средних значений для исходного набора данных. При уменьшении длины цикла относительно средней продолжительности поездки отклонение результатов растет. Согласно [13] наилучшие результаты могут быть получены при синтезе циклов, близких по длине к среднему значению для исходного набора данных. Так как цепи Маркова используют вероятностный подход при синтезе решения, целесообразно также оценить влияние распределения отклонений исходного набора данных на результаты синтеза.
Целью данной работы является разработка алгоритма генерации ездового цикла, а также самого ездового цикла, описывающего движение автомобиля в крупном российском городе Москва. Результаты этого исследования могут быть применены для создания методик испытания российских электромобилей и новых моделей автомобилей, оснащенных двигателями внутреннего сгорания.
Обработка данных
Для синтеза ездового цикла методом цепей Маркова в качестве исходных данных использовались показания GPS-трекера, установленного на тестовом автомобиле, в течение 3 месяцев. Использованные данные содержали ошибки, связанные с качеством приема сигнала, и перед использованием подверглись очистке.
Основные шаги алгоритма генерации показаны на рис. 1.
Рис. 1. Алгоритм синтеза ездового цикла
Fig. 1. The algorithm for synthesizing the driving cycle
Данные были подготовлены по методике, описанной в [14]. Данные, полученные непосредственно с GPS приемника, содержали как пропущенные значения NaN (not a number), так и неправильные измерения. Измерения, в которых значения были пропущены, удалялись из набора данных. На основании данных о скорости были рассчитаны ускорения, на основании данных об ускорениях была проведена фильтрация участков с неестественно высоким ускорением (более 3 м/с2). Микроциклы представляют собой единичные поездки, долговременные стоянки были исключены. Скорость автомобиля в начале и конце каждого микроцикла равна 0, а критерием окончания микроцикла являлась остановка автомобиля более чем на 5 мин. Так как GPS-трекер выдает значения с непостоянной частотой, то в данных могут быть пропуски, и возникает необходимость выровнять данные в микроциклах по регулярной сетке с шагом 1 с. Также это важно для реализации алгоритма синтеза, т. к. наличие неравных промежутков времени не позволит создать матрицу переходов.
Для оценки характеристик микроцикла и их расчета за основу был взят набор критериев из работы [14]. В качестве критериев были выбраны следующие значения:
– средняя скорость
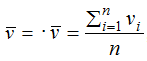
– среднеквадратичное отклонение скорости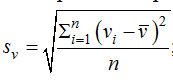 
– время равномерного движения 
,
при условии, что 
– время стоянки 
, при условии, что 
– время движения с ускорением 
при условии, что vi > 5 км/ч и ai > 0,3 м/с;
– время торможения 
при условии, что vi > 5 км/ч и ai < –0,3 м/с;
– среднее ускорение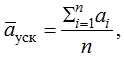 
при условии, что vi > 5 км/ч и ai > 0,3 м/с;
– среднеквадратичное отклонение ускорения 
при условии, что vi > 5 км/ч и ai > 0,3 м/с;
– среднее замедление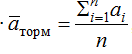 
при условии, что vi > 5 км/ч и ai < –0,3 м/с;
– среднеквадратичное отклонение замедления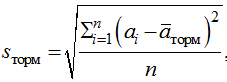 
при условии, что vi > 5 км/ч и ai < –0,3 м/с;
– 95 % перцентиль скорости;
– 5 % перцентиль замедления;
– 95 % перцентиль ускорения;
– удельный расход энергии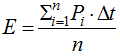 
где Pi – мощность, затрачиваемая на движение в момент времени i;
– среднее время поездки 
где tпоездки – длительность одной поездки из набора данных; k – количество поездок в наборе данных. Для оценки линейной зависимости между параметрами набора оценочных критериев была рассчитана матрица корреляции, приведенная на рис. 2.
Рис. 2. Матрица корреляции
Fig. 2. Correlation matrix
Элементы матрицы, расположенные на диагонали, имеют максимальное значение равное 1, а остальные ячейки матрицы корреляции несут информацию о степени зависимости между соответствующими парами параметров. Значения коэффициента корреляции от 0,7 до 1 и от –0,7 до –1 свидетельствуют о наличии прямой или обратной линейной зависимости между параметрами. Первые 4 параметра не имеют корреляции с остальными, и их можно считать независимыми параметрами.
После вычисления средних значений критериев для всего набора данных были вычислены максимальные отклонения значений критериев каждого отдельного цикла из набора данных от средних. Максимальное отклонение имеет два выраженных пика (рис. 3).
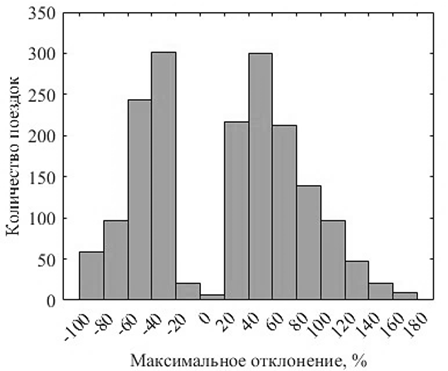
Рис. 3. Распределение максимального отклонения параметров цикла от средних значений, полученных для всего набора данных
Fig. 3. Distribution of the maximum deviation of the cycle parameters from the average values obtained for the entire data set
Количество циклов, имеющих максимальное отклонение ±20 %, составляет 27 шт. в данном наборе данных, а само распределение максимального отклонения не имеет характера нормального распределения. Основная идея синтеза цикла методом цепей Маркова состоит в том, что цепочка состояний, которые чаще всего повторяются в наборе данных, представляет собой решение, наиболее приближенное к искомому ездовому циклу, параметры которого будут иметь наименьшее отклонение от средних значений для всего набора данных. Но
т. к. основная часть циклов имеет максимальное отклонение от –20 до –80 % и от +20 до +80 %, то можно предположить, что при синтезе значительная часть результатов будет иметь значительные отклонения значений критериев от средних для всего набора данных (см. рис. 3).
Для синтеза ездового цикла был применен алгоритм на основе цепей Маркова. Алгоритм цепей Маркова устанавливает зависимость между текущим и последующим состоянием системы через вероятность перехода:
где P – вероятность перехода системы из состояния Xn в Xn+1; Xn, Xn+1 – случайные величины, представляющие состояние системы в момент времени n и n + 1; sn, sn+1 – значения случайных величин в момент времени n и n + 1.
Каждое последующее состояние определяется только текущим состоянием, а вероятность выбора следующего состояния определяется вероятностью перехода, вычисленной на этапе составления матрицы переходов. Перед началом синтеза последовательности методом цепей Маркова необходимо сгенерировать матрицу вероятности переходов,
в которой каждое состояние кодируется комбинацией скорости vn и ускорения αn. Матрица представляет собой массив, содержащий перечень всех возможных состояний, часть матрицы переходов схематично представлена на рис. 4.
При синтезе ездового цикла методом цепей Маркова ездовой цикл представляет собой последовательность, в которой каждое последующее состояние vt + 1, αt+1 зависит только от предыдущего сос-
тояния vt, αt. Значения скорости и ускорения в следующий момент времени t + 1 могут быть получены:
где ∆ν, ∆α – приращения скорости и ускорения.
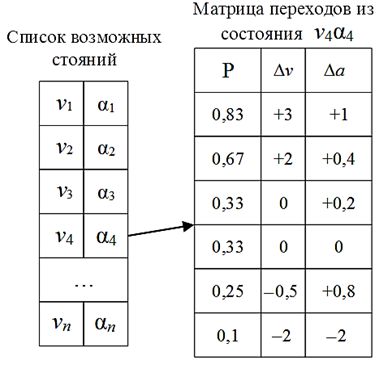
Рис. 4. Матрица возможных состояний и матрица переходов для одного из состояний
Fig. 4. A matrix of possible states and a transition matrix for one of the states
Для оценки синтезированной последовательности применятся набор критериев, описываемых системой функций
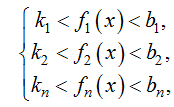
где 
– параметры из набора критериев; kn, bn – верхний и нижний предел значений оценочного параметра, при котором считается, что синтезированная последовательность ему удовлетворяет.
Сгенерированный цикл считается удовлетворяющим условиям набора критериев, если максимальное отклонение каждого из 15 оценочных параметров лежит в диапазоне ±5 % от среднего для всего набора данных. В процессе синтеза было сгенерировано 25 000 циклов, распределение максимального отклонения для сгенерированных данных представлено на рис. 5.
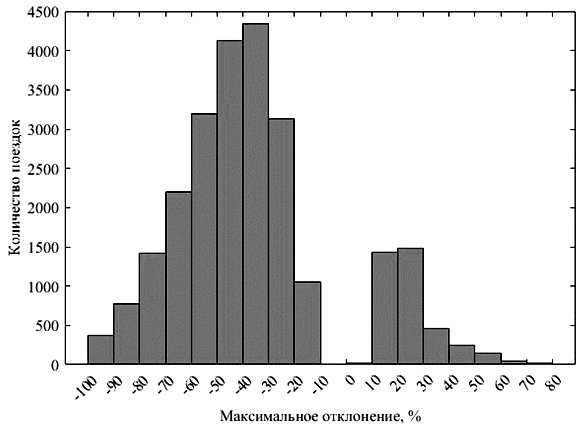
Рис. 5. Распределение максимального отклонения параметров цикла от средних значений, полученных для сгенерированных данных
Fig. 5. Distribution of the maximum deviation of the cycle parameters from the average values obtained for the generated data
Предполагалось, что для синтетических данных общий характер распределения ошибки должен был сохраниться, а на рис. 5 можно наблюдать два характерных пика. Но для сгенерированных данных наблюдается, что большинство решений имеют отклонение от –100 до –10 %. При этом количество решений, которые были бы близки к требуемым значениям, остается минимальным.
Наилучший результат из 25 000 сгенерированных решений представлен на рис. 6, а значения его характеристик и их отклонений представлены в таблице.
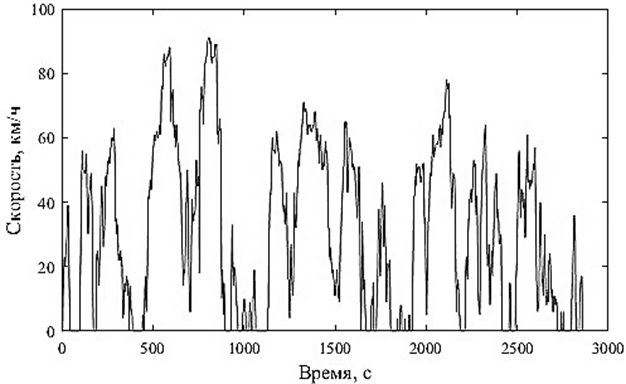
Рис. 6. Синтезированный цикл с минимальным отклонением параметров от средних значений для набора данных
Fig. 6. Synthesized cycle with minimal deviation of parameters from the average values for the data set
Сравнение параметров синтезированного ездового цикла и средних значений для набора данных
Comparison of synthesized driving cycle parameters and average values for a data set
|
Критерий |
Синтезированный цикл |
Средние значения для набора данных |
Отклонение, % |
|
Время равномерного движения, % |
22,288 |
21,504 |
–3,647 |
|
Время стоянки, % |
20,888 |
21,521 |
2,942 |
|
Время движения с ускорением, % |
30,475 |
29,482 |
–3,37 |
|
Время торможения, % |
26,347 |
27,491 |
4,164 |
|
95 % перцентиль скорости, м/с |
77 |
73,386 |
–4,924 |
|
95 % перцентиль ускорения, м/с2 |
1,6 |
1,602 |
0,141 |
|
5% перцентиль замедления, м/с2 |
–1,6 |
–1,694 |
5,587 |
|
Средняя скорость, км/ч |
39,494 |
40,613 |
2,755 |
|
Среднеквадратичное отклонение скорости, км/ч |
22,073 |
20,925 |
–5,486 |
|
Среднее ускорение, м/с2 |
0,601 |
0,643 |
6,527 |
|
Среднее замедление, м/с2 |
–0,695 |
–0,688 |
–1,085 |
|
Среднеквадратичное отклонение ускорения, м/с2 |
0,571 |
0,609 |
6,267 |
|
Среднеквадратичное отклонение замедления, м/с2 |
0,655 |
0,646 |
–1,429 |
|
Удельное энергопотребление, Дж/м |
288,875 |
296,231 |
2,483 |
Наибольшее отклонение составило 6,527 % при длине цикла 2 875 с.
Как видно из представленных результатов, решение задачи синтеза ездового цикла методом цепей Маркова возможно, но занимает значительное время.
Заключение
Максимальное отклонение, представляющее наибольшее отклонение любого оценочного параметра от соответствующих средних значений для всего набора данных, может влиять на процесс синтеза последовательностей методом цепей Маркова. Распределение максимального отклонения оказывает влияние на репрезентативность результатов синтеза. Максимальное отклонение отражает наибо-
льшее отклонение параметров синтезированного ездового цикла от средних значений. Если максимальное отклонение для некоторых исходных ездовых циклов велико, это указывает на то, что некоторые поездки в наборе данных значительно отклоняются от среднего поведения. При синтезе ездового цикла с использованием цепей Маркова эти отклонения могут привести к циклу, который либо переоценивает, либо недооценивает определенные типы поведения при вождении. Если матрица переходов построена для данных с высокими максимальными отклонениями, то синтезированный цикл может содержать экстремальные участки, которые не являются типичными, что потенциально влияет на репрезентативность для реальных условий вождения. Цепи Маркова используют вероятности перехода между состояниями для генерации синтетических последовательностей. Если максимальное отклонение высоко, это говорит о том, что в наборе данных есть значительная изменчивость. Эта изменчивость может привести к менее стабильным вероятностям перехода, что может быть причиной менее точного нахождения закономерностей в данных. Высокие максимальные отклонения также могут указывать на наличие выбросов или редких событий в наборе данных. Эти выбросы могут непропорционально влиять на вероятности перехода, что приводит к синтезированному циклу вождения, который переоценивает редкое или экстремальное поведение. Бимодальное распределение максимальной ошибки предполагает, что в исходном наборе данных есть две отдельные группы поездок. Это распределение может указывать на наличие двух различных режимов вождения (например, вождение в городе и на шоссе). При синтезе ездового цикла методом цепей Маркова могут возникнуть трудности с балансировкой этих двух режимов, что может привести к циклу, который неточно отражает истинное распределение поведения водителя. Например, синтезированный цикл может переоценивать один режим за счет другого.
Наличие высоких максимальных отклонений может повлиять на надежность процесса синтеза ездового цикла. Если максимальное отклонение велико, небольшие изменения в наборе данных (например, добавление или удаление нескольких поездок) могут привести к значительным изменениям в синтезированном цикле. Эта чувствительность может затруднить создание ездовых циклов.
При проверке синтезированного ездового цикла максимальное отклонение может служить полезной метрикой для оценки того, насколько хорошо цикл фиксирует изменчивость в исходном наборе данных. Если значения параметров, используемые для оценки ездового цикла, в синтезированном цикле значительно отличаются от средних значений в исходном наборе данных, это может указывать на то, что набор критериев недостаточен для описания данных.
Обработка исходного набора данных и распределения отклонений значений параметров элементов набора данных от средних значений имеют влияние на успешность синтеза при помощи алгоритмов, основанных на цепях Маркова. Наиболее предпочтительным является нормальное распределение ошибки, т. к. в этом случае матрица переходов будет содержать информацию о последовательности, которая может дать минимальное отклонение. В представленном случае распределение ошибки носило сложный характер и незначительное количество элементов набора данных имело минимальное отклонение от среднего. В таком случае следует использовать другие алгоритмы синтеза на основе нейросетевых моделей или вариационных автокодировщиков.
1. Topić J., Škugor B., Deur J. Synthesis and Feature Selection-Supported Validation of Multidimensional Driving Cycles // Sustainability. 2021. V. 13. N. 9. P. 4704.
2. Grinin V., Shkarupelov E., Muravev A., Kartashov A. Method for applying vehicle driving cycles to assess the durability of electromechanical transmissions of trucks // E3S Web Conf. 2023. V. 402 (7). P. 10008.
3. Geslin A., Xu L., Ganapathi D., Moy K., Chueh W., Onori S. Dynamic cycling enhances battery lifetime // Na-ture Energy. 2024. V. 10 (2). P. 172–180.
4. Baure G., Dubarry M. Synthetic vs. Real Driving Cycles: A Comparison of Electric Vehicle Battery Degradation // Batteries. 2019. V. 5. N. 2. P. 42.
5. Al-Wreikat Y., Serrano C., Ricardo S. Driving behav-ior and trip condition effects on the energy consumption of an electric vehicle under real-world driving // Applied Energy. 2021. V. 297. P. 117096.
6. Meddour A., Rizoug N., Babin A. The influence of driving cycle characteristics on motor optimisation for electric vehicles // 2022 30th Mediterranean Conference on Control and Automation (MED). Vouliagmeni, Greece: IEEE, 2022. P. 43–48.
7. Kamble S. H., Mathew T. V., Sharma G. K. Development of real-world driving cycle: Case study of Pune, India // Transp. Res. Part Transp. Environ. 2009. V. 14. N. 2. P. 132–140.
8. Anida I. N., Salisa A. R. Driving cycle development for Kuala Terengganu city using k-means method // Int. J. Electr. Comput. Eng. IJECE. 2019. V. 9. N. 3. P. 1780.
9. Fotouhi A., Montazeri-Gh M. Tehran Driving Cycle Development Using the K-Means Clustering Method // Sci. Iran. 2013. V. 20. N. 2. P. 286–293.
10. Dabčević Z., Škugor B., Topić J., Deur J. Synthesis of Driving Cycles Based on Low-Sampling-Rate Vehicle-Tracking Data and Markov Chain Methodology // Energies. 2022. V. 15. N. 11. P. 4108.
11. Yang Y., Zhang Q., Wang Z., Chen Z., Cai X. Markov chain-based approach of the driving cycle development for electric vehicle application // Energy Procedia. 2018. V. 152. P. 502–507.
12. Esser A., Rinderknecht S. Process for the Validation of Using Synthetic Driving Cycles Based on Naturalistic Driving Data Sets // 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC). 2020. P. 1–6.
13. Zhao B., Hofman T., Lv C. Intelligent Synthesis of Driving Cycle for Advanced Design and Control of Power-trains // 2018 IEEE Intelligent Vehicles Symposium (IV). Changshu: IEEE, 2018. P. 1608–1613.
14. Torp E., Önnegren P. Driving Cycle Generation Us-ing Statistical Analysis and Markov Chains. Linköping University, Department of Electrical Engineering, 2013. Report No. LITH-ISY-EX-13/4670-SE.
