Россия
Трудность проектирования трала обуславливается тем, что его характеристики должны не только учитывать особенности распределения и поведения объекта лова, но и соответствовать тяге лебедок и траулера. Для этого проектировщик должен как можно более точно рассчитать сопротивление траловой системы, которое складывается из сопротивления канатно-сетной части, деталей оснастки, траловых досок, ваеров и пр. Цель настоящей работы – определить сопротивление траловых мешков для разноглубинного трала 18/95 м с различным поворотом ромбовидной дели: Т0, Т90, где Т0 – стандартное положение ячеи, Т90 – ячея, повернутая на 90°. Были проведены эксперименты в гидроканале ООО «Фишеринг Сервис». Модель тралового мешка, закрепленная на обруче, который обеспечивает раскрытие с заданной посадкой ux, располагалась в исследовательском и экспериментальном секторе, а навстречу ей двигался поток воды. Скорость потока устанавливалась в диапазоне от 1,2 до 2,5 м/с. Как только скорость потока становилась постоянной и траловый мешок принимал правильную форму, с помощью тензодатчиков определялось сопротивление модели. Эксперименты в гидроканале включали в себя визуальное наблюдение за раскрытием ячей и изменением формы мешка и получение экспериментальных данных для определения гидродинамического коэффициента сопротивления для каждого тралового мешка. Полученные данные показали, что при повороте дели на 90° ячеи раскрыты больше, чем в стандартном положении, и за счет этого гидродинамический коэффициент сопротивления у тралового мешка с ячеей Т90 меньше, чем у мешка с ячеей с Т0.
ячея, сопротивление, траловый мешок, гидродинамический коэффициент сопротивления
Введение
Трал представляет собой конусообразный сетной буксируемый мешок, изготовленный из сетей и канатов [1]. Конструктивно трал имеет три части: канатную часть, канатно-сетную и траловый мешок. Траловые мешки (ТМ) являются аккумулирующими устройствами разноглубинных и донных тралов. Вследствие простой конструкции из-за давления воды на улов во время траления ТМ с положением ячеи Т0 (стандартное положение ячеи) подвержен искажению и, следовательно, основная масса дели растягивается, при этом уменьшается открытость ячеи для выхода прилова. В 90-х гг. учеными был предложен новый подход к расположению ячеи – Т90. Конструкция T90 основана на типичной ромбовидной дели, но ее необходимо повернуть на 90° (рис. 1). Многие ученые (N. Graham, F. G. O`Neill [2], H. Wienbeck и B. Herrmann [3], W. Moderhak [4], А. А. Недоступ [5, 6] и др.) провели ряд исследований для оценки влияния поворота ячеи на 90° (Т90) и утверждают, что такая дель имеет улучшенные селективные свойства траловых мешков при облове путассу или других гидробионтов, при этом выловленная рыба меньше деформируется.

а б
Рис. 1. Форма ячеи Т0 (а) и Т90 (б)
Fig. 1. Mesh shape T0 (а) and T90 (б)
Необходимо отметить, что в основном эти исследования были посвящены изучению селективных свойств дели Т90, и в большинстве работ, которые приведены выше, рассматриваются простые схематизации элементарной ячеи с масштабированием впоследствии данной схематизации на всю конструкцию ТМ, что ведет к неточностям в расчетах геометрических и силовых характеристик и неверному обоснованию раскрытия ячей и самого ТМ [6].
Цель и задачи
Отметим, что главная сложность проектирования инженерного сооружения в промышленном рыболовстве заключается в том, что характеристики разрабатываемого орудия лова должны не только учитывать особенности распределения и поведения объекта лова, но и соответствовать располагаемой тяге судна.
Гидродинамическое сопротивление сетных орудий лова является ключевым аспектом при проектировании рыболовных систем.
Гидродинамическая сила возникает при движении объекта относительно окружающей его среды, при знании направления и величины этих сил можно регулировать габаритные характеристики орудия лова, а также предугадывать его влияние на объекты лова и его поведение в среде [7].
Цель настоящей работы состоит в сравнении гидродинамического сопротивления ТМ с различным поворотом ячеи: Т0, Т90.
Для определения раскрытия ячеи по чертежам разноглубинного трала 18/95 м были изготовлены две модели четырехпластных мешков с различной ориентацией дели Т0, Т90: с шагом ячеи a = 8,0 мм и диаметром нити d = 1,0 мм, количеством ячей по высоте ТМ m = 200 шт. и его длине n = 320 шт. (рис. 2) [8].
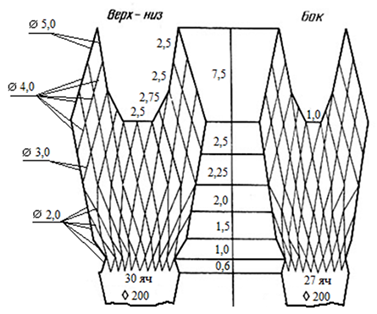
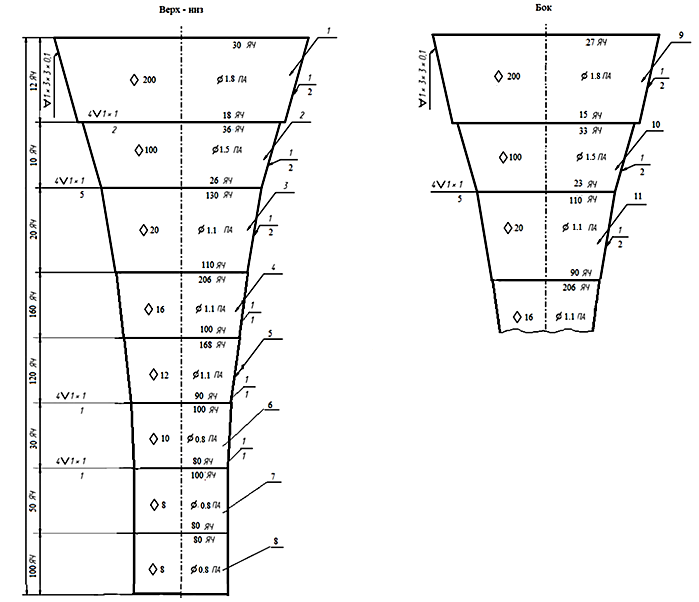
Рис. 2. Модель разноглубинного трала 18/95 м
Fig. 2. Midwater trawl model 18/95 m
Далее, модели ТМ верхней кромкой рассаживались на металлические обручи разного диаметра: D1 = 350 мм; D2 = 540 мм; D3 = 640 мм, которые обеспечивают раскрытие с заданной посадкой ux (рис. 3).

Рис. 3. Посадка тралового мешка на обручи D2 = 540 мм (а) и D1 = 350 мм (б)
Fig. 3. Landing TС on hoops D2 = 540 mm (a) and D1 = 350 mm (б)
Материал и методика
Установлено, что гидродинамический коэффициент сопротивления траловой оболочки зависит от следующих параметров [9]:
cx = f(Re, F0, α),
где Re – число Рейнольдса; F0 – сплошность траловой оболочки; α – угол атаки меридиана траловой оболочки.
Число Рейнольдса (Re) можно определить, используя формулу
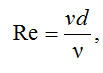
где d – диаметр нити, мм; v – скорость движения воды, м/с; ν – коэффициент кинематической вязкости воды, м2/с.
Сила сопротивления Rx ниток сетной оболочки в водной среде в общем виде выражается следующей формулой [9]:
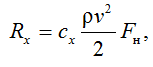 (1)
(1)
где cx – гидродинамический коэффициент сопротивления ТМ; ρ – плотность воды (1 000 кг/м3); v – скорость движения воды, м/с; Fн – площадь ниток ТМ, м2.
Из формулы (1) следует, что cx можно найти по формуле
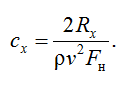 (2)
(2)
С целью определения гидродинамического коэффициента сопротивления ТМ были проведены эксперименты в гидроканале ООО «Фишеринг Сервис» (рис. 4).

Рис. 4. Гидроканал ООО «Фишеринг-Сервис»
Fig. 4. Hydrochannel of Fishering Service LLC
Эксперименты в гидроканале позволяют сформировать поток по всему объему канала, имитируя буксировку ТМ. Скорость потока можно регулировать от 0 до 2,5 м/с, задавая данные с пульта управления потоком воды. Над рабочим участком в пульте управления расположены приборы контроля и аппаратура управления характеристиками потока (рис. 5).
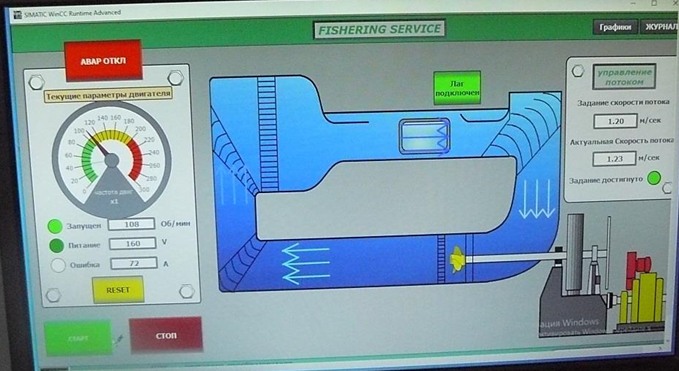
Рис. 5. Пульт управления потоком воды в гидроканале
Fig. 5. Control panel for water flow in the hydraulic channel
Обруч с расположенной на нем моделью был установлен параллельно тензодатчикам, что нивелирует угол атаки меридиана ТМ (рис. 6).
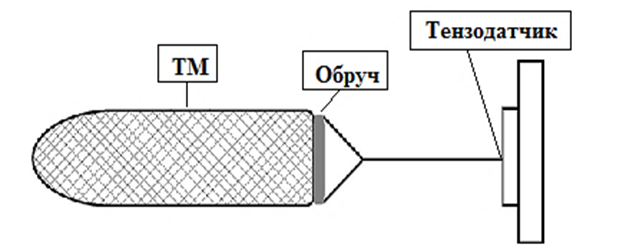
Рис. 6. Схема расположения тралового мешка в гидроканале ООО «Фишеринг Сервис»
Fig. 6. Diagram of the trawl bag location in the hydraulic channel of Fishering Service LLC
Известно, что сплошность сетной части трала определяется по формуле
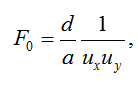 (3)
(3)
где a – шаг ячеи, мм; ux – горизонтальный коэффициент посадки; uy – вертикальный коэффициент посадки.
При заданном диаметре устья ТМ определим коэффициенты посадки ux и uy по формулам
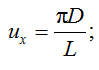 (4)
(4)
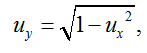 (5)
(5)
где D – диаметр обруча, м; L – длина ТМ, м.
Для определения площади ниток ТМ необходимо умножить сплошность ТМ на габаритную площадь Fг:
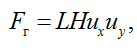 (6)
(6)
где Н – высота ТМ, м.
Также в ходе экспериментов велось видеонаблюдение, что позволило визуально оценить форму ТМ при различном положении дели четырехпластного мешка (рис. 7, 8).

Рис. 7. Форма тралового мешка Т0 при D2 = 540 мм
Fig. 7. Form T0 at D2 = 540 mm

Рис. 8. Форма тралового мешка Т0 при D1 = 350 мм
Fig. 8. Form T0 at D1 = 350 mm
Проведенные эксперименты наглядно демонстрируют, что конструкция ТМ оказывает существенное влияние на геометрию ячеи. Визуально заметна разница в распределении нагрузки в моделях ТМ с делью Т0, Т90.
Также было выявлено непропорциональное распределение продольной нагрузки по ТМ в связи с тем, что шворочные швы имитируют роль каркаса сетной конструкции и часть продольной нагрузки приходится на них, что, в свою очередь, снимает нагрузку с ячей ТМ. По результатам визуального исследования можно заключить, что с увеличением пластей в мешке увеличится и раскрытие ячей [10].
Результаты
Для определения коэффициента сопротивления металлических обручей формулу (2) необходимо привести к следующему виду:
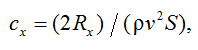
где S – площадь обруча, м2.
Площадь обруча находится по формуле
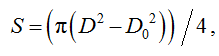
где D0 – внутренний диаметр обруча, мм.
Полученные экспериментальные расчетные данные были сведены в табл. 1.
Таблица 1
Table 1
Экспериментальные и расчетные данные обручей
Experimental and calculated hoop data
|
D, мм |
S ∙ 10–3, м2 |
v, м/с |
Rх обруч, Н |
cх |
|
350 |
5,42 |
1,2 |
3,2 |
0,8 |
|
1,8 |
5,4 |
0,6 |
||
|
2,5 |
15,2 |
0,8 |
||
|
540 |
8,4 |
1,2 |
3,8 |
0,6 |
|
1,8 |
9,0 |
0,7 |
||
|
2,5 |
22,0 |
0,8 |
||
|
640 |
9,75 |
1,2 |
4,2 |
0,6 |
|
1,8 |
11,2 |
0,7 |
||
|
2,5 |
25,8 |
0,8 |
С использованием данных, полученных в гидроканале, и формул (2)–(6), был определен гидродинамический коэффициент сопротивления для каждого ТМ при разном диаметре обруча и скорости траления (табл. 2, 3).
Таблица 2
Table 2
Расчетные данные тралового мешка с делью Т0
Calculated data of the trawl сod-end with netting T0
|
D, мм |
v, м/с |
Rх общ, Н |
Rx, Н |
cx ∙ 10–3 |
|
350 |
1,2 |
16,8 |
13,6 |
9,22 |
|
1,8 |
24,8 |
19,4 |
5,85 |
|
|
2,5 |
39,7 |
24,5 |
3,83 |
|
|
540 |
1,2 |
21,0 |
17,2 |
12,00 |
|
1,8 |
33,0 |
24,0 |
7,23 |
|
|
2,5 |
53,3 |
31,3 |
4,89 |
|
|
640 |
1,2 |
23,6 |
19,4 |
13,00 |
|
1,8 |
39,0 |
27,8 |
8,38 |
|
|
2,5 |
63,0 |
37,2 |
5,81 |
Таблица 3
Table 3
Расчетные данные тралового мешка с делью Т90
Calculated data of a trawl сod-end with netting T90
|
D, мм |
v, м/с |
Rх общ, Н |
Rx, Н |
cx ∙ 10–3 |
|
350 |
1,2 |
15,4 |
12,2 |
8,27 |
|
1,8 |
22,0 |
16,6 |
5,00 |
|
|
2,5 |
38,0 |
22,8 |
3,56 |
|
|
540 |
1,2 |
18,8 |
15,0 |
10,00 |
|
1,8 |
30,4 |
21,4 |
6,45 |
|
|
2,5 |
51,4 |
29,4 |
4,59 |
|
|
640 |
1,2 |
23,0 |
18,8 |
13,00 |
|
1,8 |
37,6 |
26,4 |
7,96 |
|
|
2,5 |
62,0 |
36,2 |
5,66 |
Для полученных данных были построены зависимости Rx от v (рис. 9, 10) при различном диаметре обруча.
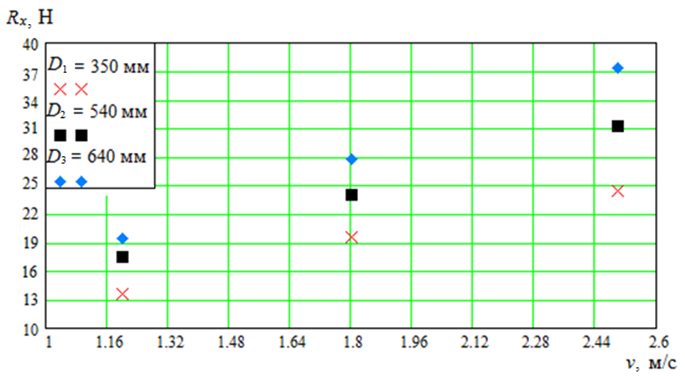
Рис. 9. Зависимость Rx от v для тралового мешка с делью Т0
Fig. 9. Dependence of Rx on v for TС with T0
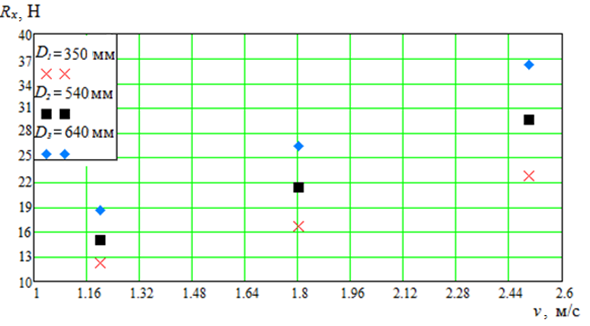
Рис. 10. Зависимость Rx от v для тралового мешка с делью Т90
Fig. 10. Dependence of Rx on v for TС with T90
На рис. 11 и 12 изображены графики зависимостей гидродинамического коэффициента сопротивления ТМ с делью Т0 и Т90 от числа Рейнольдса.
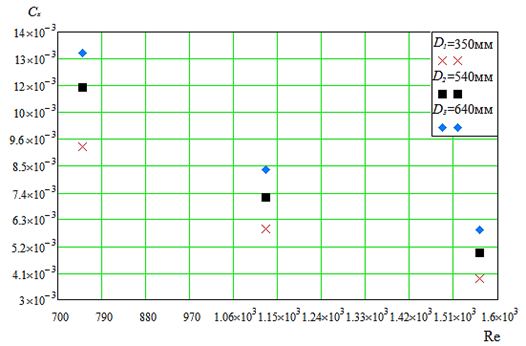
Рис. 11. Зависимость сx от Re для тралового мешка с делью Т0
Fig. 11. Dependence of сx on Re for TС with T0
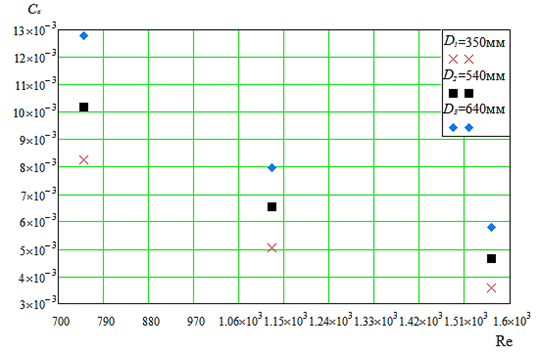
Рис. 12. Зависимость сx от Re для тралового мешка с делью Т90
Fig. 12. Dependence of сx on Re for TС with T90
Таким образом, при разных диаметрах обруча и различной скорости траления модель с делью Т90 имеет меньший гидродинамический коэффициент сопротивления, чем модель Т0 (см. рис. 9, 10).
Следует отметить, что фото и видеоматериалы для определения точных параметров формы ячеи непригодны, т. к. неизвестный радиус кривизны поверхности ТМ искажает ее фактический размер на снимке.
Заключение
В статье представлен алгоритм расчета гидродинамического коэффициента сопротивления тралового мешка с делью Т0, Т90. По результатам проведенных экспериментов можно утверждать, что конструкция тралового мешка оказывает существенное влияние на форму ячеи, а с увеличением скорости траления и диаметра обруча увеличивается и гидродинамический коэффициент сопротивления.
При сравнении моделей с различной ориентацией ячеи было доказано, что при повороте дели на 90° ячея остается открытой, в связи с чем гидродинамический коэффициент сопротивления тралового мешка уменьшается.
1. Фридман А. Л. Теория и проектирование орудий промышленного рыболовства. М.: Лег. и пищ. пром-сть, 1981. 327 с.
2. Graham N., O’Neill F. G., Fryer R. J., Galbraith R. D., Myklebust A. Selectivity of a 120 mm diamond codend and the effect of inserting a rigid grid or a square mesh panel // Fisheries Research. 2004. V. 67. P. 151–161.
3. Herrmann B., Wienbeck H., Moderhak W., Stepputtis D., Krag L. The influence of twine thickness, twine number and netting orientation on codend selectivity // Fisheries Research. 2013. V. 145. P. 22–36.
4. Moderhak W. A theoretical approach to selectivity of cod-ends // Contributions on the Theory of Fishing Gears and Related Marine Systems. 2003. V. 3. P. 105–116.
5. Недоступ А. А., Коновалова К. В., Насенков П. В., Ражев А. О., Альтшуль А. Б., Федоров С. В. Относительная жесткость рыболовных крученых изделий // Вестн. Астрахан. гос. техн. ун-та. Сер.: Рыбное хозяйство. 2020. № 1. С. 46–60.
6. Недоступ А. А., Коновалова К. В., Наумов В. А. Численное решение задачи определения конструктивных, геометрических и силовых характеристик элементарной ячеи // XX Междунар. Балт. мор. форум (Калининград, 26 сентября – 01 октября 2022 г.): сб. тр. в 7 т. Калининград: Изд-во КГТУ, 2022. Т. 2. С. 245–249.
7. Осипов Е. В. Моделирование рыболовных систем на основе объектно-ориентированных технологий: дис. … д-ра техн. наук. Владивосток, 2007. 242 с.
8. Недоступ А. А., Ражев А. О., Насенков П. В., Львова Е. Е., Сысенко В. В., Аскаров Д. В., Белозёр И. С. Экспериментальные исследования разноглубинного трала 18/95 м на оз. Виштынецкое // Вопр. рыболовства. 2023. Т. 24 (2). С. 92–98.
9. Флетчер К. Вычислительные методы в динамике жидкости. М.: Мир, 1991. Т. 1-2. 1054 с.
10. Недоступ А. А., Павленко А. А. Обоснование расчета характеристик траловых мешков // Рыбное хозяйство. 2011. № 2. С. 101–103.
















