с 01.01.2019 по 01.01.2024
с 01.01.2019 по 01.01.2024
Россия
Выполнено математическое описание процесса автоклавной обработки изделий из ячеистого бетона как нестационарного объекта управления в условиях распределенности параметров в форме системы дифференциальных уравнений в частных производных. В уравнениях учитывается тепло- и массоперенос как в среде автоклава, так и в массивах ячеистого бетона, а также процесс диффузии пара через пограничный слой и внутреннее тепловыделение при синтезе гидросиликатов в структуре автоклавируемого сырца в форме тоберморита. Полученная система уравнений связывается граничными условиями в соответствии с предложенной в работе схемой. На основании полученной системы дифференциальных уравнений в частных производных, а также с учетом разработанной схемы граничных условий составлена расчетная схема автоклава и соответствующая ей вычислительная модель в программной среде SOLIDWORKS Flow Simulation. Проведены численные эксперименты по оценке динамики температуры в центре и на поверхности массивов, а также в среде автоклава. Сравнение результатов численного моделирования с известными данными натурных экспериментов путем определения среднеквадратичного отклонения значений температуры в центре и на поверхности массивов ячеистого бетона подтвердили адекватность разработанной модели в условиях принятых допущений. Данные, полученные в результате численного моделирования, могут быть использованы при синтезе системы автоматического управления процессом автоклавной обработки с целью определения градиента температур в объеме автоклавируемого ячеистого бетона, что, в свою очередь, позволит оптимизировать производственные процессы и повысить качество конечной продукции в условиях минимизации энергозатрат на ее производство.
математическое моделирование, численное моделирование, ячеистый бетон, тоберморит, внутреннее тепловыделение, распределенные параметры
Введение
Основным показателем качества ячеистого бетона является величина его прочности Rм. Известно, что на начальном этапе производства прочность обуславливается гидратацией цемента в составе ячеисто-бетонного сырца, однако, в отличие от пенобетона, ее конечная величина формируется за счет синтеза гидросиликатов кальция в структуре ячеистого бетона [1] в форме тоберморита и ксонотлита [2]. Анализ представленных в [2, 3] исследований показывает, что преобладающей фазой в структуре автоклавного бетона, характеризующей его конечную прочность, является тоберморит, для формирования которого необходимо создать в среде автоклава определенные температурно-влажностные условия.
При построении алгоритмов управления данным энергоемким технологическим процессом на современных предприятиях по производству автоклавных ячеистых бетонов не учитывается динамика формирования гидросиликатов в форме тоберморита, продолжительность автоклавной обработки не зависит от свойств исходного сырья и рецептуры автоклавируемых массивов, а прочность готовых изделий определяется путем проведения лабораторных испытаний после завершения всех технологических операций. В результате наблюдается значительный разброс величины прочности готовых изделий в пределах одной марки по плотности [4]. Такого рода нестационарность также приводит к увеличению энергозатрат на изготовление данного вида строительных материалов, т. к. процесс выдержки изделий в автоклаве может продолжаться после достижения ими требуемой прочности. Данная проблема может быть решена путем оснащения автоклавного участка системой автоматического управления (САУ), учитывающей физико-химические процессы, протекающие в массивах сырца ячеистого бетона в процессе твердения, в том числе повышение прочности автоклавируемых изделий в ходе экзотермического синтеза тоберморита. Для создания такой САУ в первую очередь требуется разработка математического описания технологического процесса автоклавной обработки изделий из ячеистого бетона как нестационарного объекта управления в условиях распределенности параметров, чему и посвящена настоящая работа.
Определение объекта управления
Технологический процесс автоклавной обработки представляет собой совокупность нескольких последовательных этапов, при которых в среде автоклава и объеме ячеистого бетона создаются необходимые условия для формирования конечной прочности ячеисто-бетонных изделий [5]. В рамках данного научного исследования рассматриваются этапы подъема давления и выдержки изделий в автоклаве [6], при которых в условии достижения массивами ячеисто-бетонного сырца температуры не ниже ~165 °С в его структуре синтезируется тоберморитовая фаза, что сопровождается внутренним тепловыделением и придает ячеистому бетону, произведенному по автоклавной технологии, дополнительную, по сравнению с безавтоклавной технологией, прочность.
Таким образом, под объектом управления понимается совокупность тепло- и массообменных процессов, а также диффузия пара и внутреннее тепловыделение при синтезе гидросиликатов в форме тоберморита в ячеистом бетоне на этапах подъема давления и выдержки изделий в автоклаве.
Обобщенная структура процесса автоклавной обработки как объекта управления может быть представлена в виде обобщенной структуры (рис. 1).
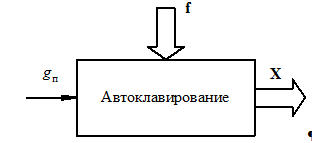
Рис. 1. Обобщенная структура процесса автоклавной обработки: gп – расход пара, подаваемого в автоклав;
X – вектор выходных координат; f – вектор возмущающих воздействий
Fig. 1. Generalized structure of the autoclave treatment process: gc – steam consumption supplied to the autoclave;
X is the vector of output coordinates; f is the disturbance vector
На входе объекта формируется управляющее воздействие – расход gп пара, подаваемого в автоклав, с характерными для каждого из рассматриваемых этапов автоклавной обработки параметрами температуры Tп и давления Pп. Состояние объекта характеризуется вектором выходных координат X = [Tм (x, y, z, t), Tавт, Pавт, Tст, Rм], где Tм(x, y, z, t) – распределение температуры в объеме массива, Tавт, Pавт – температура и давление пара в автоклаве соответственно; Tст – температура стальной стенки автоклава, Rм – прочность ячеистого бетона. Возмущающее воздействие на объект управления – вектор f = [Qтб, Tо.с], включающий внутреннее тепловыделение Qтб при образовании гидросиликатов кальция в форме тоберморита и температуру Tо.с окружающей среды, определяющей тепловые потери через ограждающие конструкции автоклава.
Допущения
Считаем, что химико-минералогический состав всех запариваемых массивов сырца является одинаковым и постоянным для заданной марки бетона по плотности, что соответствует использованию исходных компонентов из соответствующих неизменяемых месторождений.
Принимаем, что ячеистая структура массивов является равномерной и однородной (в том числе благодаря применению вибровспучивания на этапе заливки ячеисто-бетонной смеси в форму).
Допускаем, что, учитывая существующую инерционность процесса и необходимость обеспечения технологически верного выполнения подготовительных этапов продувки и вакуумирования, температура массивов и автоклава равны, т. е. Tм = Tавт.
Считаем, что в процессе автоклавной обработки при достижении массивами ячеистого бетона температуры 165 °C в их объеме начинается процесс внутреннего тепловыделения, обусловленный химической реакцией формирования гидросиликатов кальция только в форме тоберморита.
Принимаем, что температура среды, окружающей автоклав, постоянна и соответствует среднегодовому значению (~5,7 °С) для Самарской области.
Допускаем, что удаление конденсата происходит мгновенно, а тепловые потери и изменение параметров среды в автоклаве при этом несущественны.
Принимаем, что в объеме массива сырца швы после технологической операции струнной резки отсутствуют, а параметры стальных элементов внутренних конструкций учитываются при задании толщины стальной стенки автоклава.
Расчетная схема процесса
При решении поставленной задачи воспользуемся упрощенной расчетной схемой автоклава при производстве ячеисто-бетонных изделий (рис. 2).
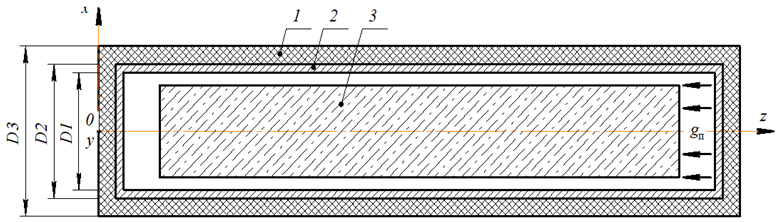
Рис. 2. Расчетная схема процесса автоклавной обработки изделий из ячеистого бетона:
1 – теплоизоляция; 2 – стальная стенка; 3 – ячеистый бетон;
D1 – внутренний диаметр стальной стенки; D2 – внешний диаметр стальной стенки и внутренний диаметр
теплоизоляции; D3 – внешний диаметр теплоизоляции; gп – расход пара; x, y, z – пространственные координаты
Fig. 2. Calculation scheme of the autoclave treatment of cellular concrete products: 1 – thermal insulation; 2 – steel wall;
3 – cellular concrete; D1 – internal diameter of steel wall; D2 – external diameter of steel wall and internal diameter
of thermal insulation; D3 – external diameter of thermal insulation; gп – steam flow; x, y, z – spatial coordinates
Здесь автоклав может быть представлен в виде двухслойного цилиндра, состоящего из слоя теплоизоляции 1 и стального корпуса 2, внутри которого располагается массив 3 сырца ячеистого бетона. В пространство между массивом и стальным корпусом через одну из стенок корпуса подается пар с расходом gп по заданной программной траектории. При достижении массивом температуры 165 °С в объеме автоклавируемого изделия начинается процесс внутреннего тепловыделения, обусловленного экзотермической реакцией синтеза гидросиликатов в форме тоберморита.
Математическое описание
Математическое описание процесса автоклавной обработки как нестационарного объекта управления в условиях распределенности параметров включает в себя тепло- массообменные процессы во внутренней среде автоклава (динамика текучей среды – пара), тепло- и массообмен в твердом теле (массивы ячеистого бетона, стальной корпус, теплоизоляция), которые связываются краевыми (граничными и начальными) условиями. Динамика паровой среды может быть описана следующей системой уравнений, которая включает уравнения движения газа (пара) по трем координатам (уравнение Навье – Стокса для декартовых координат); законы сохранения массы (уравнение неразрывности) и энергии
в условиях ее диссипации; уравнение термодинамического состояния пара; уравнения, связывающие коэффициент вязкости пара и его температуру,
а также давление и концентрацию пара; дифференциальное уравнение массопроводности [7]:
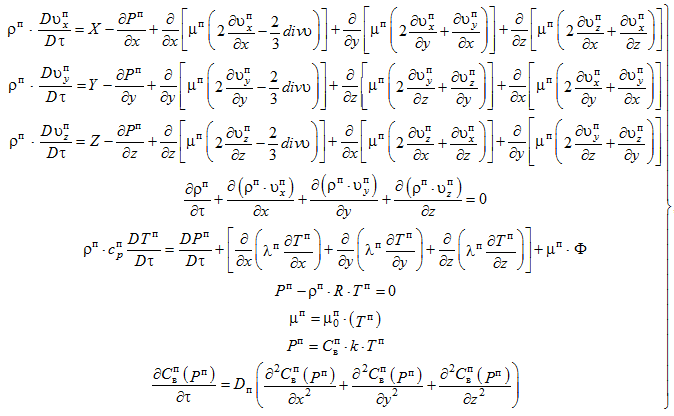(1)
где ρп, υп, Pп, Tп, λп, μп – давление, скорость, плотность, температура, коэффициент теплопроводности, удельная теплоемкость (при постоянном давлении) и коэффициент вязкости пара соответственно; 
– дивергент скорости; – скорость движения текучей среды (пара); x, y, z – пространственные координаты; τ – время; X, Y, Z – проекции
массовой силы пара, отнесенной к единице объема; k – коэффициент фильтрации [8]; 
– субстанциональные производные температуры, давления и скорости соответственно; Ф – диссипативная функция рассеивания,
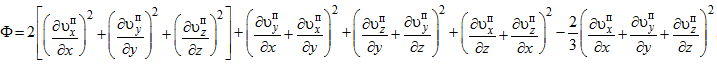(2)
где R – газовая постоянная; 
– концентрация воды в паре; Dп – коэффициент диффузии воды в среде автоклава.
Тепло- и массообмен (молекулярная диффузия) в массивах ячеистого бетона, а также теплообмен в стальном корпусе и слое теплоизоляции, согласно [9], могут быть представлены следующей системой уравнений:
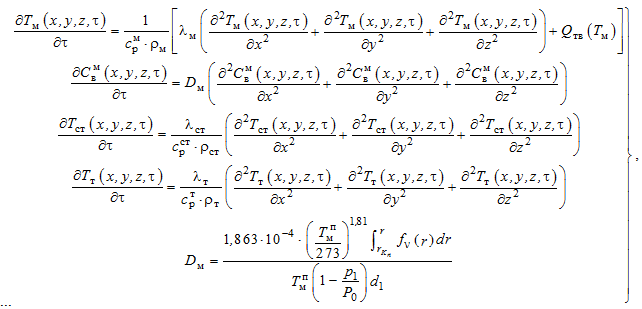(3)
где Tм, Tст, Tт, 
, ρм, ρст, ρт, λм, λст, λт – температура, удельный коэффициент теплоемкости, плотность и коэффициент теплопроводности ячеисто-бетонных массивов, стальной стенки и слоя теплоизоляции автоклава соответственно; 
– концентрация воды в массивах ячеистого бетона; 
– давление и температура пара в порах массивов ячеистого бетона, принимаем 
массива при соответствующем давлении 
– удельная объемная тепловая мощность внутреннего тепловыделения при образовании гидросиликатов в форме тоберморита в объеме массивов сырца ячеистого бетона в функции температуры массивов; Dм – коэффициент молекулярной диффузии водяного пара в массиве ячеистого бетона; 
– максимальный радиус капилляра, где возможно кнудсеновское течение; r – радиус капилляров ячеистого бетона (r = 0,8–1,5 мм для бетона марки D400); p1 и P0 – давление водяного пара и общее парогазовой смеси соответственно; d1 – коэффициент извилистости пор.
Разработанные системы уравнений (1)–(3) могут быть связаны краевыми условиями в соответствии со схемой граничных условий (рис. 3).
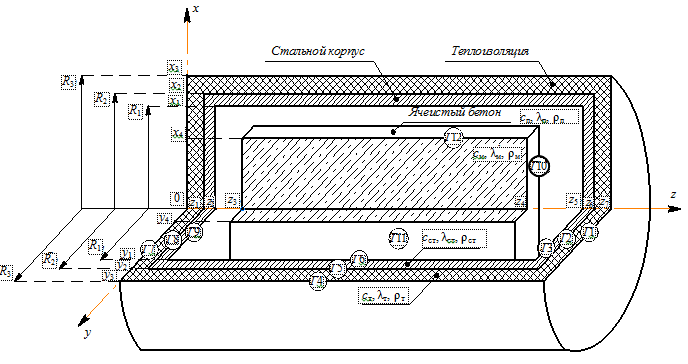
Рис. 3. Схема граничных условий: Г1–Г12 – граничные условия; R1–R3 – радиусы границ раздела сред;
x1–x4, y1–y4, z1–z7 – координаты граничных условий; сп, см, сст, ст, ρп, ρм, ρст, ρт, λпб, λм, λст, λт – удельный
коэффициент теплоемкости, плотность и коэффициент теплопроводности пара, ячеисто-бетонных массивов,
стальной стенки и теплоизоляции автоклава соответственно
Fig. 3. Scheme of boundary conditions: Г1–Г12 – boundary conditions; R1–R3 – radii of the interfaces between materials;
x1–x4, y1–y4, z1–z7 – coordinates of boundary conditions; сп, см, сст, ст, ρп, ρм, ρст, ρт, λпб λм, λст, λт – specific
heat capacity, density and thermal conductivity of steam, cellular concrete massifs,
steel wall and thermal insulation of the autoclave, respectively
При определении начальных условий рассматривается начальный момент технологического этапа подъема давления в автоклаве. Тогда в качестве начальных условий принимается:
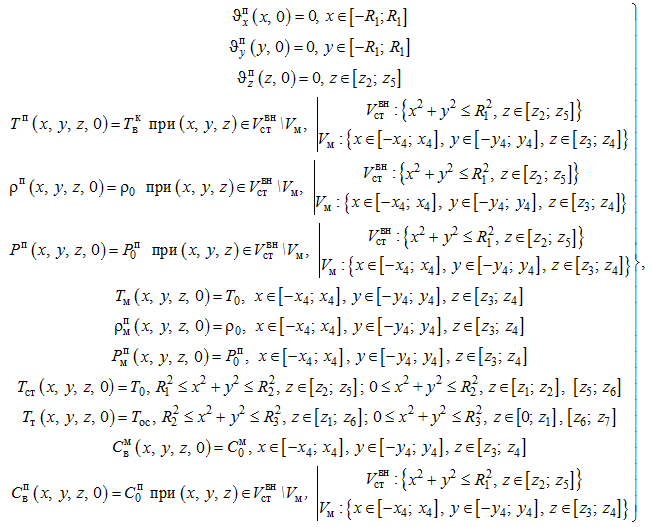(4)
где знак «\» – исключение из объема, указанного до знака, объема, указанного после знака; 1–3-е уравнения – линейная скорость движения пара по соответствующим координатам; 4-е уравнение – температура пара 
= 35 °С в автоклаве к концу этапа вакуумирования, когда давление внутри автоклава составляет Pвк = 56 кПа; уравнение 5 формирует соответствие плотности пара ρп начальной плотности ρ0 при нормальных условиях; 6–7-е уравнения показывают соответствие температур материала Тм и стальных элементов внутренней конструкции автоклава Тст начальной температуре T0, достигаемой на промежуточном этапе подогрева ячеистого бетона в камере предварительной выдержки с квазистационарным температурным режимом, включая продувку в автоклаве, допуская, что за время вакуумирования температура поверхности массивов ячеистого бетона и стальных элементов внутренней конструкции автоклава не изменяется; 8-е уравнение – температура теплоизоляции автоклава Тт равна температуре окружающей среды Тос; 9 и 10-е уравнения – концентрация воды в массиве ячеистого бетона и в паровой среде автоклава, равные 
соответственно, которые определяются применяемой рецептурой и параметрами внешних условий в процессе предварительной выдержки.
Для определения граничных условий теплообмена между паром и твердыми телами (как стальной стенкой автоклава, так и массивами ячеистого бетона) лучистый теплообмен может быть описан уравнением Стефана – Больцмана для абсолютно черного тела (граничные условия Г3, Г9–Г12, см. рис. 3). Кроме того, массообменные процессы на границе раздела сред между массивом ячеистого бетона и паром, в соответствии с теорией диффузии [10], могут быть описаны, применительно к рассматриваемой задаче, граничными условиями III-го рода (Г10–Г12). Таким образом, с учетом принятых допущений, система уравнений для граничных условий процесса автоклавной обработки примет вид
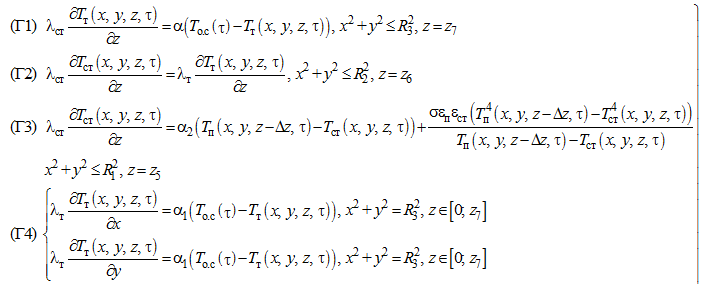
(5)
где Δz – толщина пограничного слоя между границами раздела сред; α1–α3 – коэффициенты теплообмена между поверхностью внешней футеровки автоклава и окружающей средой, стальным корпусом автоклава и паром, ячеистым бетоном и паром соответственно; σ – постоянная Стефана – Больцмана; εп, εм – степень черноты пара и автоклавируемого бетона соответственно; βп – коэффициент массообмена между паром и массивом ячеистого бетона; граничные условия Г1, Г7 и Г4 соответствуют теплообмену между окружающей средой
и поверхностью теплоизоляции по торцам [0; R3] и длине [0; z7] автоклава соответственно через коэффициент теплообмена α1. Границы Г2, Г8 и Г5 образуются между поверхностями теплоизоляции и стальным корпусом автоклава с коэффициентами теплопередачи λт, λст по торцам [0; R2] и длине [z1; z6] автоклава соответственно. Границы Г3, Г9 и Г6 соответствуют теплообмену между внутренней средой автоклава (паром) и поверхностью стального корпуса автоклава по торцам [0; R1] и длине [z2; z5] автоклава соответственно через коэффициент теплообмена α2. Границы Г10–Г12 соответствуют тепло- и массообмену между внутренней средой автоклава (паром) и гранями массива ячеистого бетона по трем координатам [–x4; x4], [–y4; y4], [z3; z4] через коэффициенты теплообмена α3 и массообмена βп соответственно.
Проверка адекватности модели
Численное решение полученной системы уравнений может быть найдено методом конечных элементов в программной среде SOLIDWORKS Flow Simulation. Здесь на основе разработанного математического описания (1)–(3), с учетом начальных (4) и граничных (5) условий, создана вычислительная модель технологического процесса автоклавной обработки изделий из ячеистого бетона (рис. 4).
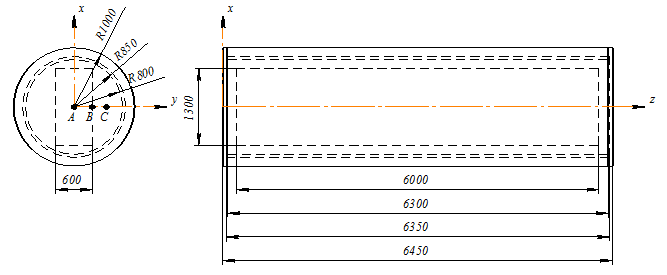
Рис. 4. Вычислительная модель технологического процесса автоклавной обработки изделий из ячеистого бетона:
A, B, C – характерные точки измерения температуры; R800–R1000 – радиусы границ раздела сред;
6000–6450 – геометрические размеры ячеистого бетона, стальной стенки и теплоизоляции
Fig. 4. Computational model of the technological process of autoclave treatment of cellular concrete products:
A, B, C – characteristic points of temperature measurement; R800–R1000 – radii of the interfaces between the media;
6000–6450 – geometric dimensions of cellular concrete, steel wall and thermal insulation
В качестве источника пара задано давление текучей среды в форме граничного условия на внутренней стенке автоклава. Динамика среды автоклава (пара) определяется из модели, полученной в [10], и задается в виде графиков зависимостей температуры Tавт(t) и давления Pавт(t) в автоклаве.
Появление внутреннего тепловыделения в массивах сырца ячеистого бетона обуславливается экзотермической реакцией образования гидросиликатов в форме тоберморита. В соответствии с [2] температура нижнего порога образования тоберморита, соответствующая началу фазовых превращений, составляет Tтб = 165 °С. Прогрев массивов ячеистого бетона происходит благодаря теплои массообмену последовательно от внешних слоев массива к внутренним. Появление внутреннего тепловыделения в каждом i-м слое будет определяться его нагревом до температуры Tмi > Tтб, где Tтб – минимально необходимая температура для образования тоберморита, а его динамика может быть описана в соответствии с разработанной авторами моделью [6] в виде симметричной гладкой кривой. Таким образом, в процессе численного моделирования общее удельное объемное внутреннее тепловыделение Qтв (3) будет определяться суммой его послойных экзотерм, динамика каждой из которых определяется как отношение величины общего внутреннего тепловыделения Qтб в соответствии с моделью [11] к объему Vi каждого i-го слоя, а время начала тепловыделения в i-м слое определяется при условии Tмi > Tтб, т. е.
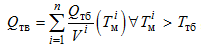, где i = 1, 2, …, n.
Кроме того, ввиду отсутствия в применяемой программной среде модуля расчета массопереноса в твердом теле, в модель может быть введен эквивалентный коэффициент теплопроводности, определяемый, с учетом известных экспериментальных данных, методом подбора. Для точного определения коэффициента тепло- и массопроводности необходимо решить обратную задачу теплопроводности [12, 13].
В условиях принятых допущений проведен ряд численных экспериментов по оценке динамики температуры в центральной части массива A и на поверхности массива B [14]. Для проверки адекватности модели реальным экспериментальным данным, приведенным в [15, 16], использован метод расчета среднеквадратичного отклонения S значений температуры в указанных точках, величина которого не превышает 5,9 °С (табл.), что подтверждает адекватность разработанной модели.
Среднеквадратичное отклонение температуры массива
The standard deviation of the array temperature
|
Экспериментальные |
S, °С |
|
|
A |
B |
|
|
[15] |
2,99 |
5,9 |
|
[16] |
5,66 |
4,95 |
Полученная модель позволяет с достаточной для инженерной практики степенью точности определить температуру в центре и на поверхности массива при известных параметрах температуры и давления паровой среды в автоклаве, а также данных о внутреннем тепловыделении в массивах ячеистого бетона при образовании тоберморита в его структуре. Применение результатов численного моделирования при синтезе системы автоматического управления данным процессом позволит получить изделия со стабильной заданной величиной прочности Rм ячеистого бетона за счет определения времени достижения изделиями требуемой температуры во всем объеме и путем вычисления на основании полученных данных времени окончания этапа выдержки массивов в автоклаве.
Заключение
Полученные результаты численного моделирования по оценке динамики температуры в центре и на поверхности массивов, а также в среде автоклава могут быть использованы при синтезе САУ процессом автоклавной обработки с целью определения градиента температур в объеме автоклавируемого ячеистого бетона, что, в свою очередь, позволит стабилизировать качественные характеристики конечной продукции в условиях минимизации энергозатрат на ее производство.
1. Книгина Г. И., Загоренко В. Д. Значение пластичности газобетонной массы при формировании макроструктуры // Строительные материалы. 1966. № 1. С. 35–36.
2. Кафтаева М. В., Рахимбаев И. Ш. Тепловыделение при синтезе гидросиликатной связки автоклавного газобетона // International journal of applied and fundamental research. 2013. № 10. C. 373–376.
3. Галицков К. С., Баранова М. Н., Болховецкий А. С. Исследование влияния структурно-фазового состава ячеистого бетона на внутреннее тепловыделение в процессе его автоклавной обработки // Градостроительство и архитектура. 2023. Т. 13. № 2 (51). С. 73–78. DOI:https://doi.org/10.17673/Vestnik.2023.02.10.
4. Клюев В. Ю. О системном разрыве между требованиями нормативных документов и современном уровне технологии ячеистого бетона // Технические науки. Научные исследования. 2008. № 2 (6). С. 58–63.
5. Галицков С. Я., Болховецкий А. С., Стулов А. Д. Структурное моделирование процессов продувки и вакуумирования ячеисто-бетонных изделий в автоклаве // Традиции и инновации в строительстве и архитектуре. Строительные технологии: сб. ст. Самара: Изд-во Самар. гос. архитект.-строит. ун-та, 2015. С. 439–441.
6. Галицков С. Я., Михелькевич В. Н., Болховецкий А. С. Идентификация тепловыделения при автоклавировании ячеистого бетона // Проблемы управления и моделирования в сложных системах: тр. XVIII Междунар. конф. (Самара, 20–25 сентября 2016 г.). Самара: ООО «Офорт», 2016. С. 346–350.
7. Ишанхождаева М. М. Физическая химия. СПб.: Изд-во СПб ГТУ РП, 2012. Ч. I. Диффузия в системах с твердой фазой. 35 с.
8. Ошкина Л. М., Сарайкин А. С. Явления массопе-реноса в капиллярно-пористых материалах // Огарёв-Online. 2015. № 13 (54). С. 1.
9. Михеев М. А., Михеева И. М. Основы теплопередачи. М.: Энергия, 1977. 345 с.
10. Лыков А. В. Теория теплопроводности: учеб. пособие для вузов. М.: Высш. шк., 1967. 599 с.
11. Галицков С. Я., Галицков К. С., Болховецкий А. С. Моделирование процесса автоклавной обработки ячеисто-бетонных изделий как объекта управления // Техника и технология транспорта. 2019. № S (13). С. 47.
12. Колибаба О. Б., Габитов Р. Н., Муратова Т. В. Математическое моделирование тепломассопереноса в слое твердых бытовых отходов в процессе его сушки // Вестн. ИГЭУ. 2016. Вып. 6. С. 43–48.
13. Мацевитый Ю. М. Обратные задачи теплопроводности: в 2-х т. Киев: Наукова думка, 2002. Т. 1. Методология. 408 с.
14. Галицков К. С., Болховецкий А. С., Заварзин А. А. Численное моделирование процесса автоклавной обработки изделий из ячеистого бетона как объекта с распределенными параметрами // Мехатроника, автоматика и робототехника. 2024. № 13. С. 115–123. DOI:https://doi.org/10.26160/2541-8637-2024-13-115-123.
15. Белкин Я. М., Хаимский З. М. Теплообмен в ячеистом бетоне и эффективные режимы автоклавной обработки // Строительные материалы. 1973. № 2. С. 31–32.
16. Глуховский В. Д., Рунова Р. Ф., Шейнич Л. А., Гелевера А. Г. Основы технологии отделочных, тепло- и гидроизоляционных материалов. Киев: Высш. шк., 1986. 303 с.
