Россия, Санкт-Петербург, г. Санкт-Петербург и Ленинградская область, Россия
Россия
Россия
Цель статьи – повышение эффективности функционирования автоматизированных систем управления (АСУ) за счет оптимизации технических средств на стадии проектирования. Для достижения поставленной цели разработаны математические модели выбора технических средств как количественно, так и на качественном уровне. Описаны основные технические характеристики средств, используемых в АСУ. Рас-смотрены показатели качества функционирования АСУ. Предложены постановка задачи выбора технических средств на этапе проектирования автоматизированных систем, исходные данные и пути решения поставленной задачи. Приведены оценки эффективности использования в автоматизированных системах различных вариантов технологических процессов. На основе полученных математических моделей решена задача выбора основных параметров комплекса технических средств АСУ. На этапе проектирования исходные данные не имеют высокой точности, ограничения, накладываемые на достоверность и время обработки отдельных порций информации, на различных участках являются условиями, наложенными на математические ожидания соответствующих случайных величин. Наличие указанных данных позволяет перейти к количественной оценке вариантов, используемой в АСУ технических средств. В процессе создания рабочего проекта уточняются исходные данные, алгоритмы и более глубоко анализируются вопросы технологии обработки информации в автоматизированных системах. В этих условиях проводятся расчеты с максимальной тщательностью. Поэтому ограничения, накладываемые на сроки решения задач и точность выходной информации, рассматриваются как ограничения на указанные случайные величины с определенным уровнем достоверности. С учетом дополнительных ограничений разработана уточненная модель расчета технических средств, необходимых при проектировании АСУ.
автоматизированные системы, технические средства, проектирование, математическая модель, эффективность, качество
Введение
Вычислительные средства, используемые в автоматизированных системах управления (АСУ), с позиции разработки делятся на следующие четыре группы [1, 2].
Первая группа обладает большими объемами памяти, высокой производительностью, сильно развитой периферией и представляет собой класс универсальных вычислительных комплексов широкого назначения. Машины этой группы снабжены мощными операционными системами, содержащими средства автоматизации проектирования программ для этих вычислительных машин.
Вторая группа имеет менее высокие характеристики памяти и производительности, однако благодаря развитой периферии и достаточно мощным операционным системам приближается к первой группе электронных вычислительных машин. Обе эти группы представляют собой универсальные вычислительные средства широкого распространения [3].
Третья группа отличается более или менее близкой совместимостью по системе команд с одним из типов машин первых групп и в то же время обладает функционально направленными операционными системами и широким набором периферийных устройств. Эти машины ориентированы на работу в составе систем управления, при этом совместимость по системе команд предполагает в некоторых случаях возможность использования универсальных вычислительных машин для отладки программного обеспечения.
Четвертая группа вычислительных средств полностью ориентирована на использование их в системах управления в качестве встроенных компонентов, характеризуется узкой ограниченностью функций операционной системы, практическим отсутствием внешних устройств и имеет ограниченный объем памяти, необходимый для решения конкретных функциональных задач. Система команд этих машин отражает специфику условий функционирования и не совместима с универсальными вычислительными средствами. К этой же группе относятся средства с системами команд, которые формируются на микропрограммном уровне.
Жесткость требований к различным параметрам вычислительных средств АСУ реального времени определяет их проблемную специализацию, что приводит к широкому распространению ЭВМ двух последних групп. Основные особенности их функционирования состоят в следующем [4–7]: необходимость учета реального времени; разветвленный обмен данными и большие объемы перерабатываемой информации; случайность поступления внешних воздействий и, как следствие, асинхронность решения разнообразных функциональных задач, подчиненных единой целевой задаче АСУ; директивные сроки решения этих задач в условиях случайности внешних воздействий; возможная нестационарность поступления входных заявок.
Помимо этого, большое значение имеет фактор длительной непрерывной эксплуатации АСУ. Это связано с тем, что после завершения разработки программы становятся недоступными для разработчика и допускается лишь эпизодическая корректировка их в процессе модернизации системы [8–11]. Большое количество эксплуатируемых систем управления, включающих вычислительные комплексы с одним и тем же комплексом программ, делает неоправданным наличие в каждом экземпляре машины технологических программ, необходимых при проектировании и не используемых при основной работе.
Кроме того, специализированные вычислительные комплексы чаще всего не имеют резерва памяти и производительности, и размещать в них мощные средства автоматизации проектирования невозможно [12–15]. Наконец, использование в большинстве случаев постоянных запоминающих устройств с механической либо электрической записью информации существенно ограничивает возможности оперативного изменения программ, что обусловливает высокие требования к качеству отработки программ до ввода их в реальные вычислительные средства.
Постановка задачи выбора технических средств
Общая задача обеспечения надежности функционирования технических средств АСУ заключается в выборе такого подмножества s множества S всех технических средств автоматизации и их вариантов, пригодных для реализации поставленных задач, которое бы максимизировало величину получаемого от АСУ экономического эффекта и не нарушало определенной логической последовательности решения этих задач, а необходимые для его реализации средства не превышали заданных или приемлемых значений.
Для математической формализации этой проблемы введем понятие решающих функций. Функция µk = 1, если k-я задача принадлежит подмножеству s, и µk = 0, если она в подмножество не входит.
В терминах решающих функций математическая постановка общей проблемы создания АСУ может быть сформулирована следующим образом: требуется найти значение вектора µk S решающих функций, при котором достигает максимального значения величина суммарного экономического эффекта, ожидаемого от его внедрения, при условии удовлетворения системы ограничений
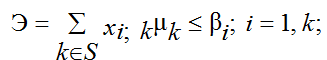
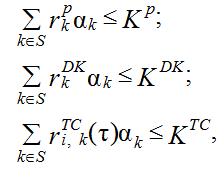
где Э – величина экономического эффекта, ожидаемого от внедрения k-й подзадачи; xi,k – коэффициент, с которым k-я решающая функция входит в i-е уравнение логических ограничений, обычно принимает значения –1,0 или +1; μk – количество решений этой задачи в течение года; βi – константа, принимающая значения 0,1 или 2; 
– дополнительные капитальные вложения в отрасль для внедрения k-й задачи; αk – решающая функция; Kp – средства на проектирование АСУ; 
– затраты на проектирование k-й задачи; KDK – средства на развитие отрасли в связи с внедрением АСУ; 
(τ) – затраты на технические средства для реализации на i-м участке k-й задачи, решаемой в момент τ; KTC – средства на приобретение техники для оснащения АСУ; k – число логических ограничений, наложенных на рассматриваемую совокупность задач.
Возможны другие ограничения, обусловленные специфическими условиями работы организации, для которой создается АСУ.
Выбор технических средств является неотъемлемой частью сформулированной задачи. Он состоит в проверке последнего из экономических ограничений на множестве рациональных вариантов технологического процесса, тесно связан с процессом проектирования и проходит несколько этапов:
– предварительный качественный отбор, основанный на качественных выводах и подкрепленный лишь грубыми количественными оценками (проводится на стадии разработки технического задания на систему);
– приближенный количественный расчет, основанный на предварительной проработке алгоритмов решения задач и технологии обработки информации в системе (выполняется на стадии технического проектирования системы);
– уточненный количественный расчет, основанный на детальном анализе вопросов разработки алгоритмов и технологии проектируемой системы (проводится на стадии рабочего проектирования системы).
Каждый следующий этап углубляет расчеты, проводимые на предыдущих этапах, на которых он базируется. Для каждого этапа может быть сформулирована своя математическая постановка задачи, которая является конкретизацией основной задачи для этого этапа.
Математическая модель выбора технических средств АСУ
Математическая модель выбора технических средств может быть сформулирована следующим образом: на основе полученных алгоритмов, технологии обработки информации, требований к сроч-
ности обработки информации и допустимой величине погрешности на каждом участке или в системе в целом найти значение вектора параметров
n = {ni}, обеспечивающее минимальное значение
,
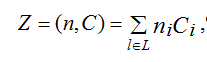где n – количество устройств различного вида; C – затраты, связанные с созданием и эксплуатацией системы на всех устройствах; L – общее количество устройств.
При условии выполнения для каждой (в данном случае k-й) задачи (порции информации) на каждом (в данном случае l-м) участке следующих ограничений:
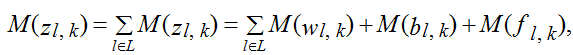
где M – математическое ожидание; z – случайная величина; w – функция распределения времени отказов, (wl,k) = (wl,k) (n); b – случайная величина, (bl,k) = (bl,k) (n); f – функция распределения времени ожидания, (fl,k) = (fl,k) (n).
На участках, работающих в режиме отказов, кроме того, должно выполняться следующее условие согласно требованиям по надежности:
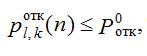
где 
– вероятность отказов задачи k на участке l; 
– вероятность отказов, заданная требованием, – постоянная величина
На участках обработки информации должны выполняться ограничения, обусловленные требуемым объемом оперативной памяти:
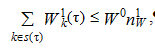
где W0 – объем оперативной памяти ЭВМ:
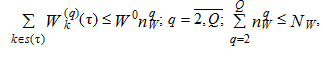
объемом внешней памяти:
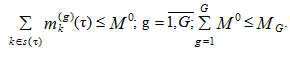
Кроме того, должны соблюдаться ограничения, накладываемые на допустимую величину погрешности, вносимую при решении каждой (в данном случае k-й) задачи (порции информации):
M(δk) ≤ δk0,
причем δk является функцией от множества принятых для проверки информации методов контроля R1:
δk = δk (R1),
где R1 
R, R – множество возможных вариантов контроля информации. Кроме того, могут быть дополнительные ограничения, наложенные структурой управляемого объекта и особенностями его работы.
Уточненная модель выбора технических средств АСУ
Как и в предыдущей модели, ограничения на объем оперативной и внешней памяти относятся лишь к участкам обработки информации. Их следует учитывать в первую очередь. Проведение этих расчетов позволяет уточнить минимально необходимую конфигурацию вычислительных средств. После этого необходимо проверить, удовлетворяет ли система защиты предъявленным к ней требованиям. В случае нарушения этих требований вносим необходимые дополнения в алгоритмы, технологический процесс и входную информацию для повышения достоверности выходной информации. Затем для каждого участка обработки информации находим функцию распределения времени обработки произвольной порции, после чего для каждого участка определяем функцию распределения времени ожидания начала обработки и функцию времени задержки после обработки, а также функцию распределения общего времени решения каждой задачи.
В заключение проверяем справедливость вероятностных ограничений, входящих в постановку задачи. Если для каких-либо задач эти ограничения не выполняются, просматривают варианты с увеличенным числом устройств в технологических цепочках решения этих задач. Принимаем вариант, обеспечивающий минимальные приведенные затраты на создание системы.
Используемые в процессе решения задачи этого этапа ограничения, накладываемые на точность выходной информации и время решения задач, в общем случае отличны от ограничений, которые учитывали на предыдущем этапе. Это объясняется тем, что здесь ограничения накладываются на значения случайных величин с некоторым заданным уровнем достоверности, ранее они накладывались на средние значения соответствующих случайных величин.
Вместе с тем случайные величины, на которые накладываются ограничения, представляют собой сумму случайных величин времени ожидания начала обработки, собственно обработки и величины последующей задержки различных порций информации. Согласно предельной теореме для суммы большого числа случайных величин получим, что при определенном числе этих слагаемых закон распределения суммарной величины близок к нормальному.
Обозначим через (Tk0)M ограничения, накладываемые на математическое ожидание, а через (Tk0)P – ограничения, накладываемые на ту же случайную величину с уровнем достоверности P0 (остальные индексы условно опущены). Предполагая, что случайные величины, из которых складывается рассматриваемая величина, имеют одинаковый закон распределения и значение дисперсии этих случайных величин совпадает со значением их математического ожидания (что характерно для потока Бернулли), получим следующее соотношение:
(1)
где N–1 – обратная функция нормального распределения (обратная функция Лапласа) с математическим ожиданием m, дисперсией σ2 и уровнем достоверности р.
В частном случае при Р0 = 0,99 получаем простое соотношение
откуда для определения (Tk0)M при заданном значении (Tk0)P получаем выражение
(2)
Соотношения (1) и (2) приближенные, т. к. они получены на основе некоторых допущений. Однако эти соотношения дают достаточно простую связь между (Tk0)M и (Tk0)P, и их можно использовать на этапе приближенного количественного расчета. Аналогичные соотношения могут быть получены для ограничений на точность выходной информации.
Характер ограничений на срочность решения задач и точность выходной информации дает разумное сочетание точности исходных данных, количества просматриваемых вариантов используемого оборудования и сложности проводимых математических расчетов. В вычислениях на этапе предварительного количественного расчета используют ориентировочные сведения о проектируемой системе. Точность их не может быть высокой. В то же время на этой стадии выбирают основной комплекс технических средств, что требует проведения большого количества расчетов, связанных с оценкой целесообразности использования этих вариантов. Поэтому в постановке задачи применяют ограничения на математические ожидания соответствующих случайных величин. Это позволяет значительно снизить трудоемкость расчетов.
На этапе уточненного количественного расчета точность исходных данных значительно выше. Кроме того, основной состав комплекса технических средств, используемых в системе, уже выбран. Здесь лишь уточняют конфигурацию оборудования. Поэтому в постановке задачи используют ограничения на случайные величины с определенным уровнем достоверности, что дает возможность максимально полно использовать разработанный математический аппарат.
В некоторых случаях дополнительные ограничения могут существенно упростить решение задачи выбора технических средств.
Анализ первичных и вторичных потоков в некоторых практических случаях позволяет дать математическое описание каждого участка обработки информации независимо от функционирования связанных с ним других участков. При этом основными параметрами, определяющими его работу, являются тип и количество используемой аппаратуры в рассматриваемом звене.
Заключение
Разработана математическая модель, позволяющая на этапе проектирования АСУ выбирать необходимое количество технических средств.
В процессе создания рабочего проекта уточняются исходные данные, алгоритмы и более глубоко анализируются вопросы технологии обработки информации в системе. В этих условиях целесообразно проводить расчеты с максимальной тщательностью, поэтому ограничения, накладываемые на сроки решения задач и точность выходной информации, можно рассматривать как ограничения на указанные случайные величины с определенным уровнем достоверности.
1. Абдулханова М., Воробьев В. А. Технологии производства материалов и изделий и автоматизация технологических процессов на предприятиях дорожного строительства: учеб. пособие. М.: Солон-пресс, 2016. 564 c.
2. Безменов В. С., Ефремов В. А., Руднев В. В. Автоматизация процессов дозирования жидкостей в условиях малых производств. М.: Ленанд, 2017. 216 c.
3. Царев Р. Ю., Пупков А. Н., Огнерубова М. А., Сержантова М. В., Бесчастная Н. А. Модель анализа надежности распределенных вычислительных систем // Вестн. Сибир. гос. аэрокосм. ун-та им. акад. М. Ф. Решетнева. 2013. № 1 (47). С. 86–91.
4. Бородин И. Ф. Автоматизация технологических процессов и системы автоматического управления (ССУЗ). М.: КолосС, 2006. 352 c.
5. Брюханов В. Н. Автоматизация производства. М.: Высш. шк., 2016. 367 c.
6. Грекул В. И., Коровкина Н. Л., Богословцев Д. А. Автоматизация деятельности предприятия розничной торговли с использованием информационной системы Microsoft Dynamics NAV: учеб. пособие. М.: Бином, 2017. 182 c.
7. Дастин Э., Рэшка Д., Пол Д. Тестирование программного обеспечения. Внедрение, управление и автоматизация / пер. с англ. М. Павлов. М.: Лори, 2017. 567 c.
8. Капустин Н. М., Кузнецов П. М. Автоматизация производственных процессов в машиностроении. М.: Высш. шк., 2017. 415 c.
9. Клюев А. С., Ротач В. Я., Кузищин В. Ф. Автоматизация настройки систем управления. М.: Альянс, 2015. 272 c.
10. Кукуй Д. М., Одиночко В. Ф. Автоматизация литейного производства. Минск: Новое знание, 2018. 240 c.
11. Латышенко К. П., Головин В. В. Автоматизация измерений, контроля и испытаний. Курсовое проектирование. М.: Изд-во МГУИЭ, 2016. 196 c.
12. Латышенко К. П. Автоматизация измерений, испытаний и контроля. М.: Изд-во МГУИЭ, 2016. 312 c.
13. Левицкий В. С. Машиностроительное черчение и автоматизация выполнения чертежей. М.: Высш. шк., 2018. 435 c.
14. Максименко А. Е., Проскуряков Н. Е. Автоматизация кузнечно-штамповочного производства. М.: Изд-во МГИУ, 2007. 192 c.
15. Мауэргауз Ю. Е. Автоматизация оперативного планирования в машиностроительном производстве. М.: Экономика, 2017. 287 c.
