Институт экономических исследований Дальневосточного отделения Российской академии наук (старший научный сотрудник Приморской лаборатории)
Россия
Рассматривается понятие и методология расчета параметров транспортной логистической сети как явления в современной логистике, расширяющего понятие «логистической цепочки» с уровня взаимодействия двух организаций до уровня внутрирегионального и межрегионального взаимодействия промышленных групп в рамках региональной транспортной сети. Примером этому могут служить параллельные товарные потоки между Азией и Европой через Суэцкий канал, через мыс Доброй Надежды и через Северный морской путь. Дан ответ на вопрос, почему логистические потоки одновременно существуют на параллельных маршрутах при разном уровне стоимости перевозки, в то время как логично было бы предположить, что логистический поток должен сосредотачиваться на наименее затратном пути. Предлагается математический аппарат для решения задачи о распределении логистических потоков внутри транспортной логистической сети, представленной в форме ориентированного графа, и определения параметров каждого сегмента установившейся транспортной логистической сети перемещения материальных ресурсов на основе взаимосвязи этих параметров. Предложенный математический аппарат позволяет установить взаимосвязи между четырьмя основными характеристиками логистического пути – стоимостью, скоростью, сохранностью и сервисом на основе их общего влияния на издержки, связанные с перевозкой по данному пути. Приведенная методика расчета позволяет оценить изменение материальных потоков по разным маршрутам при изменении материальных характеристик маршрутов – стоимости, скорости, сохранности.
транспортная логистика, логистическая цепочка, логистическая сеть, материальный поток, маршрут, путь
Введение
Современная транспортная логистика широко оперирует понятием «логистическая цепочка». В общем смысле логистическая цепочка понимается как набор последовательно соединенных, взаимодействующих, образующих систему звеньев, функционал которых в общем случае имеет целью перенос материального либо нематериального ресурса от поставщика к получателю [1]. Логистическая цепочка обычно линейна, и ее параметры на временной оси проявляются как задержка материального потока, т. е. ее звенья не обладают возможностями, позволяющими менять характер передаваемого по цепочке ресурса [2]. Каждое звено логистической цепочки представляет собой организованный процесс на пути от поставщика к получателю, например перевозку автотранспортом, консолидацию, временное хранение на складе и т. п. Характер процессов будет полностью зависеть от вида передаваемого по цепочке ресурса. Транспортные логистические цепочки чаще всего возникают внутри предприятий, а также между отдельными предприятиями для передачи отдельных видов ресурсов.
Используемое в данной статье понятие «логистическая сеть» производно от понятия «логистическая цепочка». При укрупнении масштаба рассматриваемых процессов отдельные логистические цепочки объединяются в логистические сети по передаче однородных ресурсов, и эти цепочки могут быть формализованы в виде ориентированных графов маршрутов [3]. В масштабе территории (это может быть субъект или более крупное образование, например макрорегион) могут возникать сложные транспортные логистические сети. Они всегда имеют характер ориентированных графов с циклами, поскольку, если мы уходим от понятия линейной цепочки к разветвленной сети поставок, в такой цепи всегда будут наблюдаться встречные потоки ресурсов вследствие встречной торговли ресурсами [4–6]. Такая транспортная логистическая сеть не связана с определенными ресурсами или поставщиками, поэтому представляет собой систему узлов и путей, свободных для выбора любым грузовладельцем. В логистической цепочке один ресурс всегда передается от одного поставщика одному потребителю по единственному маршруту. В логистической сети один ресурс может передаваться от нескольких поставщиков к нескольким потребителям по множеству маршрутов и различными видами транспорта одновременно: например, 70 % груза – по одному маршруту, 30 % – по другому маршруту. Логистическая сеть проявляется только при территориальном анализе, следовательно, объектом будет как минимум транспортное пространство отдельного региона, например субъекта Российской Федерации [4, 7].
Описание методологического подхода
Типичным примером транспортной логистической сети может служить логистическая сеть между Европой и Азией, состоящая из маршрутов «Азия – Суэцкий канал – Европа, Азия – мыс Доброй Надежды – Европа, Азия – Северный морской путь – Европа» (рис. 1). По теме материального потока, вовлекающего Северный морской путь, написано достаточно много работ [8–10], уже накоплен определенный опыт, и в настоящее время потоки материальных ресурсов в этой логистической сети можно считать устоявшимися, статичными на определенном интервале времени. Под статичным материальным потоком в данной работе будет подразумеваться установившийся, некоторое время действующий без изменений поток ресурсов в транспортной логистической сети. Возможно, термин несколько некорректен, но назвать поток статическим, т. е. не учитывающим параметр времени, на наш взгляд, также не вполне корректно, поскольку в описании такого потока будет участвовать время как переменная, следовательно, такой поток должен быть охарактеризован как динамический.
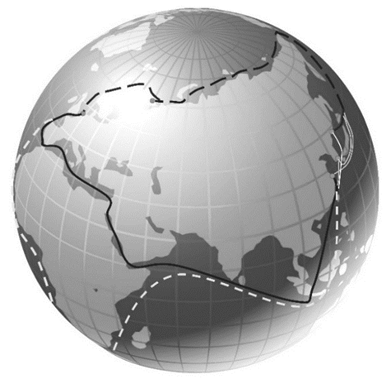
Рис. 1. Транспортная сеть между Европой и Азией
Fig. 1. Transport network between Europe and Asia
Рассмотрим транспортную логистическую сеть как объединение физических транспортных потоков, маршруты которых поддерживаются суперпозицией ветвей графа сети. Допустим, существуют один начальный А и один конечный узел сети В. Допустим, существует два или более устойчивых путей R1 … Rn транспортировки материальных ресурсов между этими узлами (рис. 2). По каждой из ветвей R1 … Rn будут перемещаться материальные ресурсы, характеризующиеся плотностью потока F1 … Fn, т. е. за интервал времени наблюдения t по ветви Ri будет перемещен физический объем ресурсов, равный Fit.
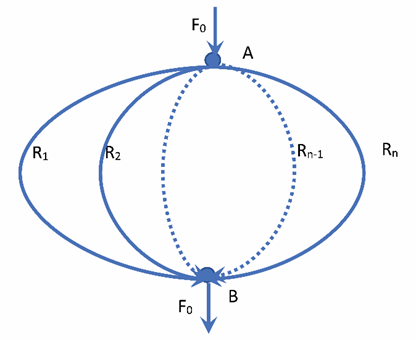
Рис. 2. Пример логистической сети с n-маршрутами
Fig. 2. Logistic network with paths – example
Предположим, что между узлами А и В логистической сети (рис. 2) существуют устойчивые материальные потоки плотностью F1 … Fn, использующие пути R1 … Rn, с общим суммарным потоком F0. Введем объективный показатель, который имеет характер обобщенных издержек, и обозначим его E (Expenses). Рассмотрим ожидаемый набор составляющих, формирующих параметр E: стоимость, скорость, сохранность и сервис.
Фактор стоимости Ci перевозки по пути с номером i определяет прямые издержки перевозки, для определения этого параметра можно использовать формулу
Ci = FitPi,
где Ci (Cost) – стоимость перевозки материального ресурса по пути i; Fi – плотность потока ресурса на пути i; t – время наблюдения; Pi – удельная стоимость перевозки на пути i.
Фактор скорости определяет интервал времени, в течение которого стоимость перевозимого груза оказывается выведенной из оборота капитала грузовладельца. Увеличение скорости перевозки уменьшает время, в течение которого материальные ресурсы остаются замороженными и не участвуют в обороте капитала. Если время перевозки равно ti, то капитал организации грузовладельца за это время должен прирасти на величину, пропорциональную jti, где j – доходность операционной деятельности грузовладельца. В данном случае используем линейную модель роста капитала, поскольку перевозка обычно не занимает много времени, а за короткие промежутки времени эффект капитализации не возникает. Тогда потери от временных затрат на перевозку по пути i будут определяться следующим образом:
Li = Fitwi(1+ jti) – Fitwi = Fiwijtti, (1)
где Li (Losses) – потери от затрат времени на прохождение грузопотоком пути i; wi – удельная стоимость ресурса на пути i; ti – время перевозки по пути i. Согласно (1) увеличение скорости перевозки приведет к уменьшению времени ti, что при сохранении величины произведения Fit, т. е. для того же перевозимого объема, приведет к уменьшению потерь Li.
Логистическая характеристика сохранности может быть выражена как стоимость потерянного грузопотока вследствие действия непредвиденных обстоятельств на пути i:
Vi = FitwiKi,
где Vi (Viability) – значение несохранности грузопотока на пути i; Ki – доля потерянного грузопотока на пути i.
Сервис представляет собой интегральное выражение в денежной форме выгод неосязаемого вида (intangible value), связанных с перемещением груза по пути i. Это единственная величина с положительным знаком среди набора составляющих, формирующих параметр E, она балансирует грузопотоки на маршрутах, проигрывающих по параметрам стоимости, скорости и сохранности:
Si = Fitvi,
где Si (Service) – значение выгод в денежном выражении от использования пути i; vi – денежное выражение удельных выгод от перевозки данного груза по пути i.
Для любого пути i на рис. 2 показатель Ei будет определяться формулой
Ei = Ci + Li + Vi – Si = FitPi + Fiwijtti + FitwiKi – Fitvi,
или
Ei = Fit(Pi + wijti + wiKi – vi).
Допустим, между точками А и В имеются устойчивые параллельные логистические потоки. Логично предположить, что в сбалансированной логистической сети параллельные маршруты используются по причине одинаковых обобщенных издержек, т. е. потери от больших затрат компенсируются большими выгодами. Следовательно, E(АВ) = const вне зависимости от выбранного пути, и для любой пары маршрутов на петле графа должно выдерживаться условие:
El(АВ) – Em(АВ) = 0, l ≠ m.
Это правило можно записать в следующем виде: в сбалансированной логистической сети сумма E по любому замкнутому контуру транспортного графа равна нулю с учетом направления логистических потоков. Последнее замечание означает, что если направление обхода замкнутого контура вдоль ветви i направлено против направления потока груза, то Ei входит в сумму с отрицательным знаком, а если эти направления совпадают, то Ei входит в сумму с положительным знаком. Расширим это положение следующим образом: при любой конфигурации логистической сети суммарная величина параметра E по замкнутому контуру транспортного графа будет равна нулю с учетом знака направления грузопотока.
Второе правило, очевидно действующее на транспортном графе, можно сформулировать следующим образом: сумма физических потоков, втекающих в любой узел транспортного графа, равна сумме физических потоков, вытекающих из этого узла. Поскольку входной поток в первый узел логистической сети F0 будет равен выходному потоку последнего узла логистической сети, число независимых уравнений потоков будет равно (k – 1), где k – число узлов в ориентированном транспортном графе, представляющем логистическую сеть.
Для конфигурации логистической сети, как на рис. 3, могут быть сформированы следующие контуры: 1-2-4-5, 1-3-4-5, 2-3. Каждый из перечисленных замкнутых контуров позволяет записать одно уравнение. Дополнить систему можно уравнениями сохранения потоков.
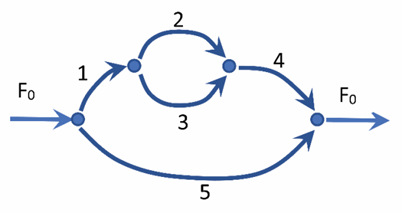
Рис. 3. Пример ориентированного графа
для формирования системы уравнений
Fig. 3. An example of a directed graph for forming
a system of equations
Поскольку в графе данной сети четыре узла, можно записать три независимых уравнения сохранения потоков:

Тогда полная система уравнений, описывающих сбалансированную логистическую сеть, показанную на рис. 2, будет записана следующим образом:

Если все уравнения приведенной выше системы
разделить на время наблюдения t, получим:
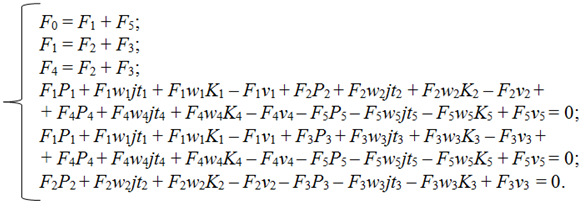 2
2
Система (2) дополняется набором ограничений Ei ≥ 0. Таким образом, формируется система уравнений, позволяющая найти неизвестные переменные сбалансированной транспортной логистической сети на основании имеющихся данных о параметрах сети. В случае системы для рис. 3 может быть найдено шесть неизвестных. Если логистическая сеть уже существует и имеет устойчивое рабочее состояние, тогда для каждого пути известны все составляющие, кроме vi. Поскольку этот параметр балансирует логистическую сеть, именно он способен превратить непривлекательный в целом маршрут в приемлемый для отдельного грузовладельца. В случае известных потоков система позволяет найти пять значений vi. В частных случаях разные компании могут использовать разные логистические маршруты, тогда вместо общего показателя доходности j в систему уравнений следует поставить показатели jk компании с номером k, использующей определенный набор логистических маршрутов либо всю логистическую сеть в целом. Описанную методику можно применять для численной оценки параметра Si, присущего маршрутам логистической сети. Если же в процессе работы логистической сети меняется один или несколько параметров, например стоимость пути, модель позволяет объективно предсказать перераспределение материальных потоков.
Применение предложенной методики для проектирования транспортной сети
Рассмотрим применение описанной методики для определения неизвестных параметров логистической сети, а именно денежного выражения удельных выгод от перевозки данного груза по пути i. В качестве примера выберем логистическую сеть на рис. 3. Как ранее указывалось, сервис в логистической сети – нематериальный параметр, поэтому в действующей логистической сети с установившимися потоками выгоды от перевозки груза по определенному пути обычно неизвестны. Задача эта решается непросто, поскольку является задачей параметрического синтеза, и поэтому ее решение обычно неоднозначно. Достаточно посмотреть на характер системы уравнений (2), чтобы сделать заключение: относительно неизвестных vi система имеет всего два линейно независимых уравнения, в то время как относительно потоков Fi в системе пять линейно независимых уравнений, и она полностью определена с учетом того, что поток F0 задан. Исходные данные для логистической сети рис. 3 приведены в табл. 1. Значение F0 = 50.
Таблица 1
Table 1
Параметры примерной логистической сети на рис. 3
The parameters of the approximate logistics network in Fig. 3
|
Путь i |
Fi |
Pi |
wi |
ti |
j |
Ki |
|
1 |
30 |
100 |
50 |
10 |
0,01 |
0,01 |
|
2 |
10 |
100 |
50 |
10 |
0,01 |
0,05 |
|
3 |
20 |
200 |
50 |
20 |
0,01 |
0,03 |
|
4 |
30 |
200 |
50 |
15 |
0,01 |
0,01 |
|
5 |
20 |
150 |
50 |
10 |
0,01 |
0,05 |
Поскольку для решения системы (2) относительно vi имеются три уравнения, из которых лишь два линейно независимы, можно найти два значения vi. Остальные три значения установим по следующим правилам. Проранжируем пути по действительной части значений Ei, т. е. по обобщенным издержкам без сервисной составляющей. Первые два из них (по числу свободных переменных в системе) приравняем к нулю, третье – к максимальному значению сервисной составляющей исходя из ограничения E1 ≥ 0. Результаты сведем в табл. 2.
Таблица 2
Table 2
Выбор минимальных сервисных значений
Selection of minimum service values
|
Путь i |
Ei |
Ei без сервиса |
Ранг Ei |
vi |
|
1 |
3 165 – 30v1 |
3 165 |
3 |
105,5 |
|
2 |
1 075 – 10v2 |
1 075 |
1 |
0 |
|
3 |
4 230 – 20v3 |
4 230 |
4 |
Вычисляемое |
|
4 |
6 240 – 30v4 |
6 240 |
5 |
Вычисляемое |
|
5 |
3 150 – 20v4 |
3 150 |
2 |
0 |
Здесь следует сделать замечание о наборах взаимозависимых vi. В системе (2) имеются следующие наборы взаимозависимых переменных vi: {v1; v2; v4; v5}; {v1; v3; v4; v5}; {v2; v3}. Приравнивать к нулю переменные vi можно только так, чтобы в каждом таком наборе оставалась как минимум одна ненулевая переменная. Фрагмент системы (2) для определения переменных vi с использованием данных табл. 1 будет выглядеть следующим образом:
3 165 – 30v1 + 4 230 – 20v3 + 6 240 – 30v4 – 3 150 + 20v5 = 0;
3 165 – 30v1 + 1 075 – 10v2 + 6 240 – 30v4 – 3 150 + 20v5 = 0;
1 075 – 10v2 – 4 230 + 20v3 = 0.
Исходя из предположений табл. 2 о значениях vi, получим:
7 320 – 20v3 – 30v4 = 0;
4 165 – 30v4 = 0;
–3 155 + 20v3 = 0.
Отсюда v3 = 157,75; v4 = 138,83.
Таким образом, вектор денежного выражения удельных выгод от перевозки данного груза v = {105,5; 0; 157,75; 138,83; 0}.
Результатом выполненных выше расчетов будет табл. 3, в которой сведены все параметры логистической сети (см. рис. 3).
Таблица 3
Table 3
Полный перечень параметров примерной логистической сети на рис. 3
The full list of parameters of the approximate logistics network is shown in Fig. 3
|
Путь i |
Pi |
wi |
ti |
j |
Ki |
vi |
|
1 |
100 |
50 |
10 |
0,01 |
0,01 |
105,5 |
|
2 |
100 |
50 |
10 |
0,01 |
0,05 |
0 |
|
3 |
200 |
50 |
20 |
0,01 |
0,03 |
157,75 |
|
4 |
200 |
50 |
15 |
0,01 |
0,01 |
138,83 |
|
5 |
150 |
50 |
10 |
0,01 |
0,05 |
0 |
Используя эти числа, можно с достаточной достоверностью предсказать изменения потоков при изменении отдельных параметров сети, например удельной стоимости перевозки Pi, или любого другого действительного параметра. Для нахождения новых значений потоков требуется решить систему уравнений (2) относительно потоков Fi, подставив в качестве параметров данные табл. 3 с учетом изменений.
Заключение
Состоятельность приведенной в данной статье методики анализа материальных потоков в транспортной логистической сети основана прежде всего на разумности действий участников рынка перевозок. Основное предположение заключается в том, что участники рынка перевозок не используют все возможные маршруты, которые можно построить, исходя из полного графа существующих путей. Если какие-то, на первый взгляд не лучшие, маршруты используются, следовательно, они приносят, кроме видимых расходов, какие-то выгоды, которые могут проявляться частным и самым неожиданным образом. Второе предположение, которое позволяет оценивать динамику материальных потоков на основе системы уравнений вида (2), заключается в том, что изменение потоков в краткосрочном периоде не влияет как на действительные, так и на нематериальные параметры транспортной логистической сети. В долгосрочном периоде взаимосвязь между величиной потоков и параметрами системы может возникнуть, если субъекты-участники процесса проявят волю.
Общая проблема методологий, которые пытаются распространить физические принципы на поведение разумных субъектов, находится в плоскости скорее метафизики, чем науки, и кроется в ответе на вопрос: что такое воля субъекта? Во всех моделях объектов экономического пространства остается один фактор, который не поддается моделированию и предсказанию – разумное поведение субъекта, участника производственных отношений, который зачастую стремится действовать против физических законов, против установленных правил, против логики, причем часто с успешным результатом. По этой причине даже хорошо продуманная, логичная и научно выверенная модель может сформировать предсказание, далекое от действительного поведения моделируемой системы, управляемой человеком.
1. Мойсеенко С. С., Мейлер Л. Е., Мороз Е. О. Организация проектирования и управления мультимодальными перевозками // Мор. интеллектуал. технологии. 2019. № 4-4 (46). С. 120–125.
2. Еловой И. А., Гончар М. А. Управление потоками в логистических цепях (теория, методология, организация): моногр. Гомель: Изд-во БелГУТ, 2020. 227 с.
3. Кузнецов А. Л., Щербакова-Слюсаренко В. Н., Семенов А. Д. Тенденции развития и устойчивость глобальной контейнерной транспортно-логистической системы // Вестн. Гос. ун-та мор. и реч. флота им. адм. С. О. Макарова. 2022. Т. 14. № 1. С. 75–86.
4. Заостровских Е. А. Возможности интеграции морского транспорта в международное транспортное пространство в условиях интенсивного освоения Восточной Арктики // Устойчивый Север: общество, экономика, экология, политика: сб. тр. VII Всерос. науч.-практ. конф., посвященной 100-летию образования Якут. АССР (Якутск, 30 ноября – 01 декабря 2022 г.). Якутск: Изд-во СВФУ, 2022. С. 249–254.
5. Краснопольский Б. Х. Влияние магистральной инфраструктуры на эффективность пространственно-хозяйственных образований: подходы к оценке // Регионалистика. 2021. Т. 8. № 3. С. 56–71.
6. Чан Я., Останин В. А. Международная политическая экономия как теоретическая база познания процессов на политических рынках // Вестн. Алтайс. акад. экономики и права. 2021. № 5-1. С. 128–134.
7. Развитие больших социально-экономических систем: Дальневосточный макрорегион: моногр. / под ред. П. А. Минакира, А. Г. Исаева. Хабаровск: Изд-во ИЭИ ДВО РАН, 2023. 352 с.
8. Вакуленко С. П., Куренков П. В. Северный морской путь в системе международных транспортных коридоров // Трансп. и логистика в Арктике. Сев. мор. путь: курс – Дальний Восток. Альм. 2016. Вып. 2. С. 212–219.
9. Лазарев В. А. Северный морской путь как фактор притяжения товарных потоков из Северо-Восточной Азии // Регионалистика. 2019. Т. 6. № 6. С. 77–87. DOI:https://doi.org/10.14530/reg.2019.6.77.
10. Лазарев В. А., Фисенко А. И. Транзитный потенциал Северного морского пути // Мор. интеллектуал. технологии. 2020. № 1-2 (47). С. 257–261. DOI:https://doi.org/10.37220/MIT.2020.47.1.085.

















