Россия
Россия
Россия
УДК 004.942 Исследование поведения объекта на основе его математической модели
Рассматривается модель безопасной эксплуатации судна при ограниченном ресурсе, в состоянии зависимости от предложенных судовыми службами значений параметров эффективности и их применения. При проекции условий, представленных данной моделью, можно обозначить ряд стратегий, которые могли бы быть оптимальны по принципу максимального гарантированного результата для судовых служб. В зависимости от количества судовых служб и исходной информированности администрации судна модель может быть оптимальной для любых систем управления безопасностью рыболовных или транспортных компаний в целом. При несении ходовой вахты судовые специалисты вынуждены оценивать состояние навигационной (или промысловой) ситуации в условиях влияния широкого круга неоднозначных, двойственных факторов. Для поддержания безопасного состояния ситуации судовыми службами реализуются запросы на ресурс. Величина ресурса всегда имеет конечное ограничение. При распределении ресурса капитан должен учитывать «потребности» всех судовых служб и обеспечить их ресурсами таким образом, чтобы безопасность навигационной (или промысловой) ситуации поддерживалась на необходимом уровне. Для этого должен быть определен максимальный уровень количества ресурса, предназначенного для той или иной судовой службы. Также важно учесть, что в любой момент времени для каждого ресурса должен быть сохранен определенный резерв. В рамках модели безопасной эксплуатации судна рассматривается схема реализации запроса на ресурс, а также процесс распределения ресурса. Рассматривается построение модели взаимоотношений судовых служб в процессе распределения ограниченного ресурса. Предлагается оценка эффективности игровой модели распределения ресурса через назначение величины относительной погрешности. Анализируется возможность возникновения ситуации равновесия интересов в системе взаимоотношений начальников судовых служб. Реализуется решение задачи безопасной эксплуатации судна посредством анализа показателей затрат ресурса и эффективности его использования.
управление состоянием судна, стратегии судовых служб, оптимальность принятия решений, максимальный гарантированный результат, ограниченный ресурс
Введение
В практике управления системой безопасной эксплуатации судна задача распределения ресурсов между судовыми службами (комплектующих изделий, оборудования и т. д.) является наиболее частой и максимально распространенной. Основным международным нормативным документом, регулирующим выполнение этих операций, является Международный кодекс по управлению безопасной эксплуатацией судов и предотвращением загрязнения (раздел 6), и на национальном уровне эти процедуры изложены в Руководстве (раздел 6) [1]. Однако, являясь обязательными для исполнения, эти руководства не содержат детализированной информации о методах обеспечения содержащихся в них требований, а лишь констатируют необходимость исполнения системы установленных правил на основе принципа достижения максимально возможной безопасности эксплуатации судна. Поэтому первоочередной задачей для успешного выполнения указанных требований является обеспечение полноты информации о самом судне и окружающей его среде. При обладании полной информационной базой естественным решением задачи распределения ресурсов между судовыми службами является применение оптимизационного подхода. Капитан в лице планирующего органа изыскивает и реализует оптимальное распределение ресурсов, обеспечивает его соответствие установленному критерию. На практике же применение оптимизационного подхода не всегда возможно [2]. Прогрессивные изменения влекут быструю сменяемость транспортных технологий, промысловых операций и затратные ресурсы не всегда своевременно могут быть отражены в эксплуатационных статьях компаний или просто отсутствуют, а существующие нормы могут быть существенно завышены от фактической потребности.
Уровень информированности о потребности в ресурсах у судовых служб выше, чем у капитана судна, поэтому распределение ресурсов обеспечивается по заявкам руководителей судовых служб.
Обычно капитан обеспечивает судовые службы ресурсами пропорционально их заявкам. Зачастую такое распределение приводит к завышению требований по заявкам, и это в свою очередь стимулирует накопление избыточности необходимого ресурса судовыми службами.
Теория организационных и организационно-технических систем дает возможность считать, что эффективность результатов деятельности судовых служб может быть значительно увеличена при обеспечении ресурсами соразмерно эффективности их использования. Поэтому представляют интерес исследования в рамках теоретико-игровых подходов и составление оптимальных моделей в зависимости от конкретных особенностей системы управления состоянием безопасной эксплуатации судна (количества служб, информированности капитана и т. д.).
Оптимальная модель в данной работе составлена на принципе распределения одного ресурса. Такая модель, с одной стороны, присуща многим практическим ситуациям, а с другой – дает возможность в расширенном формате оценить свойства эффективности результатов активности судовых служб при распределении судовых ресурсов.
Постановка задачи
Пусть в двухуровневой системе управления состоянием безопасности задано конечное множество судовых служб Q = {1, 2, ..., K}, которые, потребляя одномерный ресурс, имеющийся у капитана в количестве х0, обеспечивают безопасную эксплуатацию судна. Обозначим через xq, γq, ζq = γq / xq показатели затрат ресурса, затрат на поддержание безопасности судна и эффективности использования q-го ресурса соответственно, через yq = (xq, γq) – вектор показателей для q-й судовой службы. Тогда множество возможностей по поддержанию безопасной эксплуатации судовых средств каждой q-й службой можно записать как
(1)
где uq(xq) – функция по обеспечению состояния безопасной эксплуатации судна (предполагается непрерывной); xqmax – максимальное количество ресурса, которое судовая служба может использовать при функционировании системы.
Для каждой q Î Q определим величины
и множество Z = [ζqmin, ζqmax]. Кроме того, пусть функция uq(xq) удовлетворяет следующим условиям:
(2)
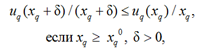(3)
а распределяемый по службам ресурс является дефицитным:
(4)
Обозначим через
множество реализуемых запросов от судовых служб на ресурс.
Пусть y* = (yq*, q Î Q) – окончательный вариант запроса. При составлении запроса у капитан судна и каждая q-я служба стремятся максимизировать свои целевые функции, соответственно определяемые выражениями
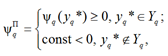(5)
где функция ψq(yq*) удовлетворяет условиям
(6)
Следовательно, капитан судна будет ориентирован к тому, чтобы намечаемый к реализации запрос на ресурс у оказался допустимым. Если величина запроса на использование ресурса у является допустимой, то выигрыш капитана будет очевидно определяться запланированным уровнем безопасной эксплуатации судна. Предположим, что капитану известны затраты на ресурс и затраты на мероприятия по обеспечению безопасной эксплуатации судна на этапе реализации и администрация вводит штрафную политику за отклонение от этих затрат. Тогда выигрыш каждой из судовых служб при получении ей нереализуемого заказа на ресурс будет заведомо меньше, чем выигрыш при любом реализуемом запросе. На множестве Yq выигрыш судовой службы монотонно возрастает с увеличением объема мероприятий по обеспечению безопасной эксплуатации судна и затрат ресурса (судовой службе «проще» не экономить ресурс).
Пусть судовой администрации известно, какое количество служб участвует в распределении и получении ресурса, свойства (1)–(6), а также такие значения ζqмин, ζqmax показателя эффективности использования ресурса, что
(7)
Распределение ресурса строится следующим образом. На 1-м этапе администрация судна выбирает и сообщает начальникам судовых служб правила распределения, в соответствии с которыми набор допустимых запросов yq(q Î Q) преобразуется в допустимое множество таких запросов y* = (yq*, q Î Q). Таким образом, для каждой q-й службы определяется зависимость ее выигрыша
от векторов показателей yq = (yk, k Î Q \ {q}), yq всей системы распределения. На 2-м этапе возникает ситуация, которую можно описать игрой K судовых служб. При этом стратегией судовой службы будет выбор запроса на ресурс yq, а выигрыш будет определяться функцией Dq(yq, yq). Для извлечения решения игры нужно, чтобы между судовыми службами (или службами и судовой администрацией) происходил обмен информацией, который может производиться, например, по схеме аукциона [3–5]. Таким образом, главным при дальнейшем исследовании функционирования игровой модели распределения ресурса при обеспечении безопасности эксплуатации судна будет являться дилемма: существуют ли решения данной игровой модели и каковы свойства этого решения.
Модель взаимоотношений судовых служб при распределении ограниченного ресурса
Обозначим через 
максимальный объем комплекса мероприятий, которыми потенциально можно при оптимальном для судовой администрации распределении ресурса поддерживать состояние безопасной эксплуатации судна. Объем комплекса мероприятий предусматривается выделенным ресурсом, полученным в соответствии с используемой игровой моделью. Эффективность игровой модели t распределения ресурса в системе обеспечения состояния безопасной эксплуатации судна будем оценивать величиной относительной погрешности
Чем меньше μ, тем более успешным будет комплекс мероприятий при выделенном ресурсе. Определим вектор
известных судовой администрации параметров возможного комплекса мероприятий с учетом модельного распределения ресурсов. Кроме того, пусть определено множество Ω(а) возможных конкретных реализаций распределения ресурсов в игровой модели в соответствии с имеющейся у судовой администрации информации (вектора а). Множество Ω(а) включает в себя условия (1)–(7) с числом судовых служб, равным заданному K. Поскольку при распределении ресурса судовой администрации известно лишь множество Ω(а) возможных реализаций, то целесообразно использовать «осторожную» оценку эффективности, записанную как
Комплекс мероприятий taopt Î T назовем оптимальным по вектору а в некотором классе механизмов Т, если
Величину
естественно рассматривать в качестве оценки погрешности распределения ресурса в комплексах мероприятий по поддержанию состояния безопасной эксплуатации судна системах из множества Ω(а).
Выделим множество запросов на ресурс, соответствующих общей форме принципа обратных приоритетов [6–9]:
(8)
(9)
где φ(ζq) – базовая функция запросов на ресурсы судовых служб, φ(ζq) = φ Î Φ, где Φ – множество дифференцируемых, монотонно возрастающих функций.
В некоторых частных случаях [10–12] запросы на выделение ресурса в виде (8), (9) могут приводить к неполному распределению ресурса, несмотря на его дефицит (4). Поэтому изменим форму запросов на выделение ресурсов, планируя вариативное распределение ресурса между судовыми службами [13].
Для этой цели определим следующие величины и множества:
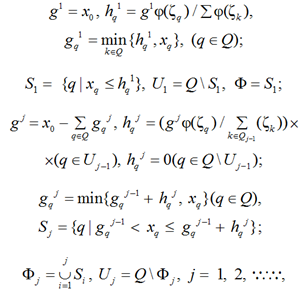
где j – номер шага алгоритма по составлению запросов на ресурс. На 1-м шаге судовые службы из множества U1 получают ресурс в количестве gq1 = hq1, а элементы из множества S1 – в количестве gq1 = xq. Остаток ресурса, составляющий величину g2, распределяется на 2-м шаге между службами из множества U1(hq2 = 0, если q Î S1). При этом службы из множества U2 получают дополнительный ресурс в количестве hq2, а службы из множества S2 – в количестве xq – hq1 и т. д. Процесс распределения заканчивается на J-м шаге, когда gj+1 = 0. Очевидно, что J ≤ K. В конце процесса распределения ресурса определяются величины xq* = gqJ(q Î Q).
Обозначим через dq(yq, yq) заданную описанным алгоритмом зависимость количества ресурса xq, выделяемого q-й службе, от векторов показателей элементов системы. Будем рассматривать в дальнейшем законы формирования запросов на выделение ресурса, которые определяются условием
xq* = dq(yq, yq) и условием (9).
Пусть q-я судовая служба предлагает плановый запрос на ресурс в количестве yq.Тогда xq*ζq ≤ uq(xq). Если xq*ζq < uq(xq), то судовая служба может предложить запрос в виде yq* = (xq, uq(xq*)), который совпадает с ответным предложением администрации на ресурс yq**. При этом
.
Следовательно, xq*ζq = uq(xq*). Из свойства (3) следует, что по величине ζq < ζqmax однозначно определяется такое количество ресурса xq(ζq), что xq(ζq) ζq = uq(xq(ζq)).
Далее примем, что
. (10)
Тогда значения показателей эффективности судовых служб ζq(q Î Q) полностью определяют выделяемое каждой q-й службе количество ресурса
максимальное количество ресурса, которое может получить судовая служба:
и ее выигрыш:
.
При этом
(11)
В связи с предположениями (3), (10) зависимость xq(ζq) оказывается непрерывной на всем интервале [ζqmin, ζqmax]. Непрерывными также будут отображения вида
Эти отображения описывают правила выборов запросов на выделение ресурса при переходе от j-го к (j + 1)-у шагу при значениях j = 1, 2, ..., J – 1. Поэтому непрерывными также будут следующие зависимости вида
.
Обсуждение полученного результата
В бескоалиционных играх часто в качестве принципа рационального поведения игроков рассматривается достижение ситуации равновесия. Из выражения (11) следует, что для существования такой ситуации:
определяемой условиями
необходимо и достаточно наличие вектора
который будет удовлетворять соотношениям
(12)
Этим соотношениям будут эквивалентны следующие:
(13)
Действительно, если ζq > ζ'q, то
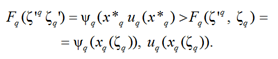
Если ζq < ζ'q, то
Поэтому если имеет место выражение (13), то выполняются и отношения (12). В то же время из свойств реализуемости запроса на выделение ресурса yq' следует, что
(14)
На основании выражений (12)–(14) можно утверждать, что в рассматриваемом взаимоотношении начальников судовых служб может существовать ситуация равновесия интересов. Однако достижение ситуации равновесия интересов является не единственным принципом рациональных действий судовых служб. Так, в условиях неполной взаимной информированности для начальников судовых служб могут представляться предпочтительными стратегии, которые позволяют им рассчитывать на максимальные гарантированные выигрыши. Кроме того, выражения (12)–(14) позволяют допустить, что у каждой судовой службы может существовать такая стратегия yq', которая гарантирует получение ресурса в количестве, не меньшем xq', при любых стратегиях остальных судовых служб.
Заключение
При управлении состоянием безопасной эксплуатации судна необходимо стремиться прежде всего к тому, чтобы формируемый запрос на ресурс оказался допустимым. Если величина запроса на этот ресурс является допустимой, то выигрыш будет очевидно определяться запланированным уровнем безопасности.
Если в случае конкурентных отношений при распределении ресурса между судовыми службами и судовой администрации известно лишь множество возможных реализаций такого распределения, то целесообразно для оценки эффективности мероприятий использовать только «осторожную» оценку.
При конкурентных отношениях между начальниками судовых служб может существовать ситуация равновесия их интересов, достижение которого является не единственным примером рациональных действий судовых служб.
В условиях неполной взаимной информированности для начальников судовых служб могут представляться предпочтительными стратегии, которые позволяют каждому из них рассчитывать на достижение максимального гарантированного выигрыша.
1. Руководство Р.033-2010. Системы управления безопасной эксплуатацией судов. Требования. Руководство Р.034-2010. Порядок проведения проверки систем управления безопасной эксплуатацией судов. URL: https: // files.stroyinf.ru / Data2 / 1 / 4293754 / 4293754830.pdf (дата обращения: 24.03.2024).
2. Вивиорра С. И., Пеньковская К. В., Меньшиков В. И. Классификация навигационных и промысловых ситуаций судовым специалистом // Вестн. МГТУ: тр. Мурм. гос. техн. ун-та. 2018. Т. 21. № 4. С. 541–547.
3. Ушаков В. А. Модельно-алгоритмическое обеспечение оперативного оценивания и анализа показателей качества управления информационными процессами // Изв. высш. учеб. заведений. Приборостроение. 2021. Т. 64. № 8. С. 688–692.
4. Симанков В. С., Астреин В. В. Основные методологические аспекты организации и функционирования систем поддержки принятия решений безопасности судовождения // Эксплуатация мор. трансп. 2016. № 2 (79). С. 56–64.
5. Кравченко Ю. А., Курситыс И. О. Комбинированный подход к решению задачи распределения ресурсов // Изв. Юж. федерал. ун-та. Технические науки. 2017. № 7 (192). С. 111–122.
6. Ризванов Д. А. Методологические основы поддержки принятия решений при управлении ресурсами в сложных системах // Вестн. Ижевск. гос. техн. ун-та им. М. Т. Калашникова. 2018. Т. 21. № 4. С. 200–207.
7. Волков В. Ф., Галанкин А. В., Жигулин Ю. А. Методика обоснования структуры системы информационного обеспечения организационно-технических систем на основе принципа гарантированного результата // T-Comm: Телекоммуникации и трансп. 2016. Т. 10. № 4. С. 52–57.
8. Бойко А. А., Дегтярев И. С. Метод оценки весовых коэффициентов элементов организационно-техни-ческих систем // Системы управления, связи и безопасности. 2018. № 2. С. 245–266.
9. Мишин А. И., Мишина С. Ю., Лаута О. С., Иванов Д. А. Организация групповой деятельности и способы взаимодействия индивидов в малых группах // Изв. Тул. гос. ун-та. Технические науки. 2023. № 8. C. 132–141.
10. Горбунова А. В., Зарядов И. С., Самуйлов К. Е., Сопин Э. С. Обзор систем параллельной обработки заявок // Вестн. Рос. ун-та дружбы народов. Сер.: Математика. Информатика. Физика. 2017. Т. 25. № 4. С. 350–362.
11. Славянов А. С. Анализ и практическое применение моделей распределения ресурсов // Бюл. науки и практики. 2018. Т. 4. № 9. С. 228–244.
12. Баркалая О. Г. Понятие конкуренции в задачах оптимального распределения ресурсов и методы ее оценки // Экономика и упр. 2021. Т. 27. № 9 (191). С. 734–740.
13. Баркалов С. А., Глушков А. Ю., Моисеев С. И. Решение задачи распределения ресурсов дискретного типа методами линейного программирования // Вестн. Юж.-Урал. гос. ун-та. Сер.: Компьютерные технологии, управление, радиоэлектроника. 2020. Т. 20. № 2. С. 26–35.
