Россия
Малорасходные турбомашины – это устройства, которые играют важную роль в приводе различных агрегатов в области судостроения, авиастроения и других отраслях тяжелого машиностроения. Они имеют некоторые преимущества по сравнению с турбиной высокой средней мощности. Наибольшее количество малорасходных турбомашин изготавливают парциальными, т. е. с частичным впуском. Рассматривается принцип турбины с частичным облопачиванием рабочего колеса как один из видов парциальных турбомашин. Исследуется влияние основной скоростной характеристики турбинной ступени на потери кинетической энергии в ступени. Моделирование газодинамических процессов, происходящих в турбинной ступени, проводилось с использованием программного комплекса ANSYS Workbench. С помощью данного комплекса была создана трехмерная геометрическая модель турбинной ступени с различной степенью облопачивания рабочего колеса. Посредством применения метода конечных элементов сгенерирована расчетная сетка, расчетная модель, а также заданы граничные условия численного эксперимента. Результатом численного эксперимента являются графики зависимости потери кинетической энергии от окружной скорости (скоростной характеристики турбинной ступени). Данная зависимость может быть представлена не только графически, но и с помощью математического аппарата. Примером такого аппарата является полиномная зависимость. Рассматриваемая математическая конструкция может применяться в целях оптимизации математических моделей течения газа в проточной части малорасходной турбины. Получены кубические двухпараметрические полиномы потерь кинетической энергии в поточной части соплового аппарата и рабочего колеса, дана оценка его применимости в действующей математической модели.
сопловой аппарат, коэффициент потерь, рабочее колесо, кинетическая энергия, численный метод, эксперимент, расчетная сетка, газодинамика, малорасходная турбина
Introduction
The vast majority of low-consumption marine turbomachines are manufactured with partial intake – partial. This is due to a number of advantages compared to the use of small full-size underwater turbines. The paper considers the very principle of a turbine with partial blading of the runner (TPBR) without reference to the thermodynamic properties of the working fluid. Low-cost marine turbines that can be considered in this study, including steam turbines, gas turbines, have their advantages and limitations. For example, steam turbines have high efficiency and good reliability, but they require large dimensions and a long time to heat. Gas turbines, on the other hand, are compact and can quickly achieve operating parameters, but their efficiency may be lower, especially at low loads. Therefore, the choice of turbine type should be based on specific requirements and operating conditions [1-4].
The optimal choice will allow achieving high efficiency of utilization turbo generators, which will lead to a reduction in fuel consumption and material costs in marine engines [5]. The use of utilization turbogenerators in collaboration with internal combustion engines is one of the measures that can improve the efficiency of marine engines. This is an important step in the development of marine energy, which will help reduce the negative impact on the environment and ensure more efficient use of resources [6].
The main graphs characterizing the efficiency of turbine stages that are found in the scientific literature are graphs of the dependence of the efficiency coefficient on u1/C0. This parameter is the main speed characteristic of the stage. According to this parameter, the optimum point of kinetic energy losses, the velocity coefficient of the nozzle diaphragm and the runner are also fixed. Determining the optimal operating mode of the turbine stage while obtaining maximum efficiency with minimal kinetic energy losses is an urgent topic for research.
Goals and objectives of the study
The purpose of this study is to obtain polynomial dependences of energy losses in the flow part of the nozzle diaphragm and runner from the main speed characteristic of the u1/C0 stage.
Research objectives:
– based on previous numerical experiments conducted in this field [7-9]. The loss coefficients in the nozzle diaphragm and runner are determined;
– the method of mathematical approximation determines the polynomial dependences of kinetic energy losses on partiality and u1/C0;
– comparison of the values of the velocity coefficients of the nozzle diaphragm and runner obtained numerically with the result of the obtained mathematical dependencies.
The article [7] examines the study of models in which the velocity coefficients of nozzle diaphragm (ND) and runner (R) are determined based on experimental data. However, using a numerical experiment, it is possible to identify the distinctive features of the flow in these models and decide on the need for a semi-experimental study of the flow characteristics in ND and R using a simulation bench. Such a study was carried out in a scientific paper [8] on a simulation stand using the ANSYS CFX software. In Fig. 1 shows one of the stages of an inflow low-consumption TPBR.
The simulation of gas dynamic processes occurring in the turbine stage in the study was carried out using the ANSYS Workbench software package [9]. With the help of this complex, a three-dimensional model of the turbine stage with varying degrees of impeller damping was created. Using the finite element method, a computational grid was generated, a computational model was created, and boundary conditions for a numerical experiment were set.
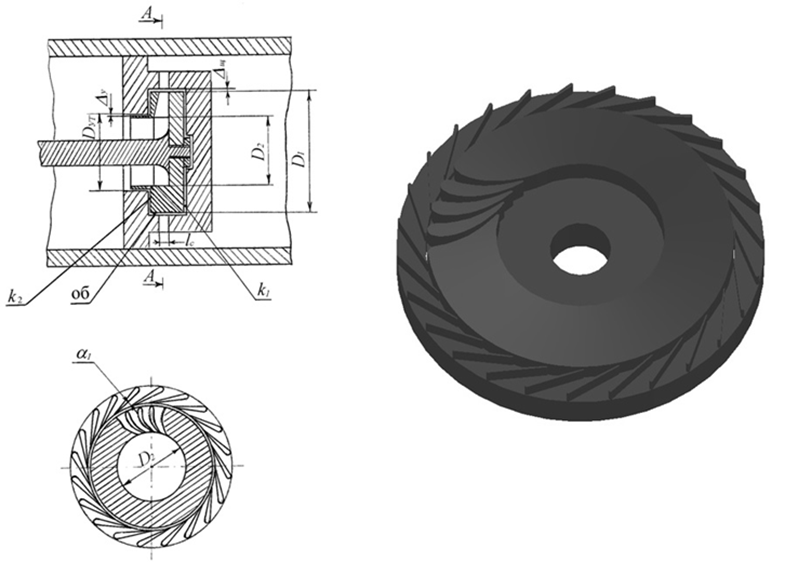
a b
Fig. 1. Diagram (a) and three-dimensional model (b) of a low-flow turbine stage
The results of the study
In [7], a TPBR was studied at various degrees of partial R. The values of the velocity coefficient ND and the velocity coefficient R were obtained. The velocity coefficients of ND and R with the energy loss coefficients in the flow part of ND and R have a certain interdependence expressed by the formulas [8]. Fig. 2 shows the dependences of the loss coefficients in the flow part of the ND for the stage in the range of ε from 0.059 to 1.00 and πt from 1.5 to 2.5 from u1/C0 [10, 11].
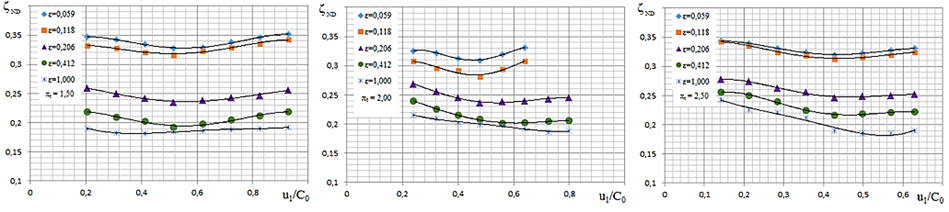 a b c
a b c
Fig. 2. Two-dimensional dependence of the loss coefficient in the flow part of ND on u1/C0 with a degree
of partiality ε from 0.059 to 1.00: a – by πt = 1.5; b – by πt = 2.0; c – by πt = 2.5
The graphs of the dependence of the loss coefficient in the flow part of ND are a graphical representation of energy losses, which can be used to create polynomials expressing the dependence of ζND on the parameters u1/C0 and ε. The loss coefficient in ND can be expressed as a function of u1/C0 has the general form:
ζND(ε) = A(u1/C0)4 + B(u1/C0)3 + C(u1/C0)2 + D(u1/C0) + E.
For each degree of partiality in the range from 0.059 to 1.00, the polynomial has coefficients shown in Tables 1-3 [12].
Table 1
Coefficients of the nozzle diaphragm unit polynomial at the degree of expansion πt = 1.5
|
Degree of partiality ε |
Coefficients of the nozzle diaphragm unit polynomial |
||||
|
A |
B |
C |
D |
E |
|
|
0.059 |
–1.271 |
2.863 |
–2.086 |
0.541 |
0.302 |
|
0.188 |
–0.871 |
1.861 |
–1.233 |
0.265 |
0.316 |
|
0.206 |
–0.529 |
1.135 |
–0.682 |
0.067 |
0.265 |
|
0.412 |
–1.142 |
2.507 |
–1.729 |
0.384 |
0.193 |
|
1.000 |
0.477 |
–1.264 |
1.212 |
–0.477 |
0.247 |
Table 2
Coefficients of the nozzle diaphragm unit polynomial at the degree of expansion πt = 2.0
|
Degree of partiality ε |
Coefficients of the nozzle diaphragm unit polynomial |
||||
|
A |
B |
C |
D |
E |
|
|
0.059 |
–11.644 |
21.558 |
–14.025 |
3.741 |
0.025 |
|
0.188 |
–6.674 |
12.729 |
–8.203 |
2.064 |
0.131 |
|
0.206 |
–1.629 |
3.023 |
–1.683 |
0.202 |
0.281 |
|
0.412 |
–1.057 |
2.116 |
–1.259 |
0.137 |
0.253 |
|
1.000 |
1.211 |
–2.474 |
1.846 |
–0.647 |
0.295 |
Table 3
Coefficients of the nozzle diaphragm unit polynomial at the degree of expansion πt = 2.5
|
Degree of partiality ε |
Coefficients of the nozzle diaphragm unit polynomial |
||||
|
A |
B |
C |
D |
E |
|
|
0.059 |
–3.947 |
6.456 |
–3.446 |
0.635 |
0.306 |
|
0.188 |
–3.508 |
5.704 |
–2.952 |
0.482 |
0.318 |
|
0.206 |
–4.588 |
7.598 |
–4.192 |
0.813 |
0.227 |
|
0.412 |
–6.856 |
11.293 |
–6.243 |
1.238 |
0.175 |
|
1.000 |
4.748 |
–6.223 |
2.919 |
–0.736 |
0.304 |
A mathematical model that allows us to determine the loss coefficient in the flow part of the ND depending on two factors (ε and u1/C0) is presented in the form of a two-parameter dependence ζND = f(ε, u1/C0), for each πt.
With the degree of expansion πt = 1.5:
ζND(ε, M1t) = 0.205 – 0.062ε – 0.002(u1/C0) + 0.083ε2 – 0.0014ε(u1/C0) + 0.0077(u1/C0)2 – 0.03ε3 + 0.0013ε2(u1/C0) – 0.0022ε(u1/C0)2 – 0.0013(u1/C0)3.
With the degree of expansion πt = 2.0:
ζND(ε, M1t) = 0.213 – 0.035ε – 0.0015(u1/C0) + 0.071ε2 – 0.001ε(u1/C0) + 0.0063(u1/C0)2 – 0.03ε3 + 0.007ε2(u1/C0) – 0.003ε(u1/C0)2 – 0.0013(u1/C0)3.
With the degree of expansion πt = 2.5:
ζND(ε, M1t) = 0.228 – 0.47ε – 0.0016(u1/C0) + 0.063ε2 – 0.0066ε(u1/C0) + 0.0072(u1/C0)2 – 0.025ε3 + 0.001ε2(u1/C0) – 0.0048ε(u1/C0)2 – 0.0026(u1/C0)3.
A graphical representation of the two-parameter dependence ζND = f(ε, u1/C0), with πt = 1.5 is shown in Fig. 3.
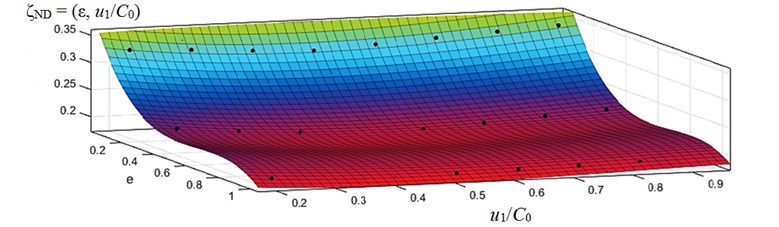
Fig. 3. Three-dimensional dependence of the loss coefficient in the flow part of the ND on u1/C0
and the degree of partiality ε, with πt = 1.5
This model makes it possible to more accurately estimate the value of ζND for various combinations of the values of ε and u1/C0. Similarly, the empirical dependences for the loss coefficient in the runner are determined (Fig. 4) [13].
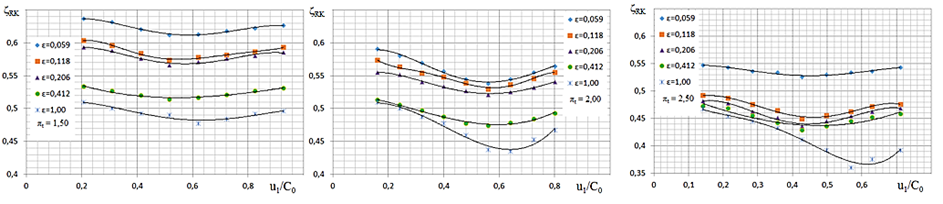
a b c
Fig. 4. Two-dimensional dependence of the loss coefficient in the flow part of R on u1/C0 with a degree
of partiality ε from 0.059 to 1.00: a – by πt = 1.5; b – by πt = 2.0; c – by πt = 2.5
The loss coefficient in R can also be expressed as a function u1/C0 has the general form:
ΖR(ε) = A(u1/C0)4 + B(u1/C0)3 + C(u1/C0)2 + D(u1/C0) + E.
For each degree of partiality in the range from 0.059 to 1.00, the polynomial has coefficients shown in Tables 4-6.
Table 4
Coefficients of the runner unit polynomial at the degree of expansion πt = 1.5
|
Degree of partiality ε |
Coefficients of the runner unit polynomial |
||||
|
A |
B |
C |
D |
E |
|
|
0.059 |
–1.205 |
2.722 |
–2.000 |
0.509 |
0.595 |
|
0.188 |
–1.106 |
2.466 |
–1.741 |
0.393 |
0.577 |
|
0.206 |
–1.374 |
3.048 |
–2.194 |
0.546 |
0.550 |
|
0.412 |
–0.723 |
1.557 |
–1.029 |
0.200 |
0.524 |
|
1.000 |
–0.646 |
1.565 |
–1.182 |
0.271 |
0.491 |
Table 5
Coefficients of the runner unit polynomial at the degree of expansion πt = 2.0
|
Degree of partiality ε |
Coefficients of the runner unit polynomial |
||||
|
A |
B |
C |
D |
E |
|
|
0.059 |
1.735 |
–1.312 |
–0.047 |
0.054 |
0.5824 |
|
0.188 |
12.288 |
–20.268 |
12.125 |
–3.207 |
0.874 |
|
0.206 |
6.000 |
–9.947 |
6.122 |
–1.744 |
0.735 |
|
0.412 |
–1.092 |
3.139 |
–2.571 |
0.695 |
0.447 |
|
1.000 |
17.107 |
–28.445 |
16.933 |
–4.440 |
0.927 |
Table 6
Coefficients of the runner unit polynomial at the degree of expansion πt = 2.5
|
Degree of partiality ε |
Coefficients of the runner unit polynomial |
||||
|
A |
B |
C |
D |
E |
|
|
0.059 |
–2.714 |
4.583 |
–2.508 |
0.468 |
0.519 |
|
0.188 |
–6.135 |
10.859 |
–6.314 |
1.309 |
0.404 |
|
0.206 |
–8.315 |
14.135 |
–7.956 |
1.621 |
0.374 |
|
0.412 |
–8.478 |
14.357 |
–8.080 |
1.655 |
0.363 |
|
1.000 |
16.260 |
–23.339 |
11.425 |
–2.426 |
0.642 |
In general, the analysis of the dependence graphs presented in Fig. 4 shows the possibility of obtaining cubic two-parameter polynomials ζR = f(ε, u1/C0).
With the degree of expansion πt = 1.5:
ζR(ε, M1t) = 0.527 – 0.072ε – 0.001(u1/C0) + 0.026ε2 + 0.0017ε(u1/C0) + 0.0085(u1/C0)2 + 0.01ε3 – 0.002ε2(u1/C0) – 0.0002ε(u1/C0)2 – 0.0002(u1/C0)3.
With the degree of expansion πt = 2.0:
ζR(ε, M1t) = 0.495 – 0.077ε – 0.016(u1/C0) – 0.001ε2 – 0.001ε(u1/C0) + 0.004(u1/C0)2 + 0.018ε3 – 0.004ε2(u1/C0) – 0.0018ε(u1/C0)2 + 0.0035(u1/C0)3.
With the degree of expansion πt = 2.5:
ζR(ε, M1t) = 0.435 + 0.49ε – 0.018(u1/C0) + 0.104ε2 – 0.0067ε(u1/C0) + 0.0081(u1/C0)2 – 0.074ε3 – 0.004ε2(u1/C0) – 0.0038ε(u1/C0)2 + 0.053(u1/C0)3.
A graphical representation of the two-parameter dependence ζR = f(ε, u1/C0), with πt = 1.5 is shown in Fig. 5.
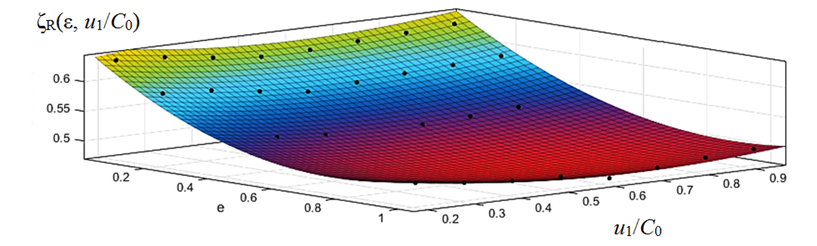
Fig. 5. Three-dimensional dependence of the loss coefficient in the flow part of the R on u1/C0
and the degree of partiality ε, with πt = 1.5
The adequacy of any mathematical model must be verified by a physical experiment. Due to the lack of results of a physical experiment on the energy loss coefficients in the flow part of the runner and nozzle diaphragm for the stage under study, the adequacy of the polynomial dependence can be performed using such an integral characteristic as efficiency.
When introducing the obtained energy loss dependencies into the existing mathematical model, the deviation of the internal efficiency between the calculated and the obtained input of the physical experiment is no more than 2.5%, which does not exceed the experimental error.
Conclusion
In the course of the study, the following tasks were completed and the relevant conclusions were obtained:
– based on previous studies, graphs of the dependence of energy losses in the flow part of ND and R on u1/C0 were constructed;
– using mathematical approximation methods, mathematical dependences of energy losses in were obtained for each degree of partiality ζND = f(ε, u1/C0) and ζR = f(ε, u1/C0);
– the obtained polynomial dependencies can be used to calculate the flow part from a turbine stage of this type and will allow modeling the parameters for further improvement.
1. Раков Г. Л., Паутов Д. В., Смирнов М. В., Кук-лина Н. И. О возможности создания утилизационных турбогенераторов с осесимметричными соплами для двигателей внутреннего сгорания // Науч.-техн. вед. Санкт-Петербург. гос. политехн. ун-та. 2015. № 3 (226). С. 7–16.
2. Чехранов С. В., Симашов Р. Р., Ханькович И. Н. Развитие теплоутилизационных технологий в судовой энергетике // Мор. интеллектуал. технологии. 2017. № 3-2 (37). С. 107–111.
3. Ерофеев В. Л., Жуков В. А., Мельник О. В. О возможностях использования вторичных энергетических ресурсов в судовых ДВС // Вестн. Гос. ун-та мор. и реч. флота им. адм. С. О. Макарова. 2017. Т. 9. № 3. С. 570–580. DOI:https://doi.org/10.21821/2309-5180-2017-9-3-570-580.
4. Матвеенко В. Т., Очеретяный В. А., Дологлонян А. В. Характеристики рабочих процессов воздухонезависимых одноконтурных микрогазотурбинных установок для подводной техники // Вестн. гос. ун-та мор. и реч. флота им. адм. С. О. Макарова. 2017. Т. 9. № 3. С. 612–618. DOI:https://doi.org/10.21821/2309-5180-2017-9-3-612-618.
5. Соловьев А. В., Чиркова М. М., Попов Н. Ф. Повышение эффективности судовых энергетических установок // Вестн. Астрахан. гос. техн. ун-та. Сер.: Морская техника и технология. 2018. № 4. С. 101–106. DOI:https://doi.org/10.24143/2073-1574-2018-4-101-106.
6. Абул К. А. Оценка возможностей утилизационных установок главных двигателей крупнотоннажных судов транспортного флота // Вестн. Астрахан. гос. техн. ун-та. Сер.: Морская техника и технология. 2009. № 1. С. 121–125.
7. Крюков А. А., Чехранов С. В. Сравнение значений коэффициентов скорости в турбинной ступени с частичным облопачиванием рабочего колеса // Вестн. Гос. ун-та мор. и реч. флота им. адм. С. О. Макарова. 2021. Т. 13. № 2. С. 257–265.
8. Крюков А. А., Куличков С. В., Ратников А. А. Моделирование потерь энергии в центростремительной турбине с частичным облопачиванием рабочего колеса // Вестн. Гос. ун-та мор. и реч. флота им. адм. С. О. Макарова. 2023. Т. 15. № 5. С. 858–866.
9. Крюков А. А. Численное исследование баланса потерь кинетической энергии в проточной части малорасходной центростремительной турбине // Вестн. Гос. ун-та мор. и реч. флота им. адм. С. О. Макарова. 2022. Т. 14. № 4. С. 583–590.
10. Чехранов С. В. Малорасходные турбины безвентиляционного типа: основы построения, математические модели, характеристики и обобщения: дис. д-ра техн. наук. Владивосток, 1999. 363 с.
11. Чехранов С. В., Симашов Р. Р. Математическая модель радиальной малорасходной турбины с частичным облопачиванием рабочего колеса // Трансп. дело России. 2015. № 6. С. 222–226.
12. Крюков А. А. Влияния угла наклона сопел на коэффициент скорости центростремительной турбины с частичным облопачиванием рабочего колеса // Вестн. Астрахан. гос. техн. ун-та. Сер.: Морская техника и технология. 2023. № 1. С. 23–29.
13. Крюков А. А. Влияния шага сопловой лопатки на коэффициент скорости центростремительной турбины с частичным облопачиванием рабочего колеса // Вестн. Гос. ун-та мор. и реч. флота им. адм. С. О. Макарова. 2023. Т. 15. № 1. С. 73–81.

















