Россия
Вопросам разработки нефтяных месторождений с применением термических методов воздействия на нефтяные пласты стали уделять большое внимание с открытием месторождений тяжелых нефтей. Теоретические исследования гидродинамики пласта, а также температурных полей в многослойных пластах, стимулировались с появлением современных ЭВМ и персональных компьютеров. Благодаря математическому описанию стали возможны гидродинамические расчеты вытеснения вязкопластичной нефти водой с аномальными свойствами. В случае вытеснения высоковязких и парафинистых нефтей холодной водой в многоcлойных пластах происходит выпадение парафина и закупорка слабопроницаемых пластов, в результате опережающего вытеснения нефти по пропласткам с высокой проницаемостью. Результаты проведенных исследований показали, что создание оторочки горячей воды на разных этапах разработки месторождений высоковязких парафинистых нефтей улучшает показатель разработки, повышает коэффициент нефтеотдачи.
залежи многофазной многокомпонентной смеси, вязкопластичная нефть, нефтяные месторождения
Введение
Запасы тяжелой вязкопластичной нефти в мире примерно в 5 раз превышает остаточных извлекаемых запасов легких нефтей малой и средней вязкости. В последние годы разработке тяжелых нефтей уделяется все большее внимание, особенно в северных районах нашей страны. Месторождения: Ромашкинское, Узеньское, Астраханское, Ярегское, Усинское, Ашальтинкое и др. [1–5] содержат значительное количество парафина, смол и асфальтенов. На месторождениях с парафинистой нефтью небольшое снижение пластовой температуры приводит к осаждению парафина и закупорке поровых каналов. Нефть становится дисперсной средой и может привести к прекращению фильтрации. Необходимо тепловое воздействие на пласт путем закачки теплой воды или горением.
Постановка задачи
Для математического моделирования движения неньютоновской жидкости предлагаются различные модификации закона Дарси. Для месторождений, где с понижением температуры (меньше 20 ºС), нефть приобретает вязкопластичные свойства, предложена модель, где фильтрация считается невозможной, а при больших градиентах фильтрации описывается законом Дарси:
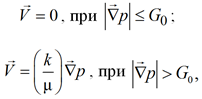(1)
где G0 – начальный градиент, который зависит от вязкости µ проницаемости k среды и температуры [1].
Зависимость градиента сдвига G0 от проницаемости рассмотрена в работах [2, 6]. Для пористой среды радиус капилляра обычно заменяют на и вводят множитель a, учитывающий связь эффективного радиуса наиболее крупных пор с проницаемостью:
(2)
где τ0 – предельное напряжение сдвига жидкости.
Для оценки значений начального градиента сдвига по предельному напряжению сдвига обычно значение коэффициента a принимают в пределах от 0,017 до 0,065.
Исследования авторов подтверждают, что разработка месторождений высоковязких и парафинистых нефтей с экономической и технологической точки зрения наиболее эффективным является закачка горячей воды и пара [1–11].
Закачка горячей воды влияет на текущую добычу нефти и конечную нефтеотдачу. Низкопроницаемые пропластки могут отключиться в двух случаях: если перепад давления мал и недостаточен для преодоления градиента сдвига; если вокруг нагнетательной скважины пласт остудился еще до прохождения фронта вытеснения до температуры застывания нефти.
Математическое моделирование
В общепринятых обозначениях для скоростей фильтрации фаз принимается
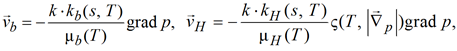(3)
где 
– скорость течения воды; kb(s, T) – проницаемость; s – насыщенность; T – температура; µb(T) – вязкость; 
– скорость течения нефти; kH(s, T) – проницаемость; µH(T) – вязкость нефти; причем структурный множитель ς в программных реализациях имеет вид [1, 2]:
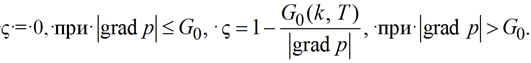(4)
В случае появления критических точек нулевой скорости появляется погрешность счета, обусловленное дисбалансом при девятиточечной и рядной системах. Для учета данного обстоятельства формулу для структурного множителя можно представить в виде [1, 2]:
(5)
где α0 – значение структурного множителя.
Относительные фазовые проницаемости нефти и воды представим в виде [1, 2]:
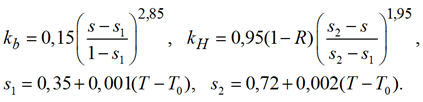(6)
Величина R = 0, если температура больше чем пластовая температура T0, вычисляемая по формуле
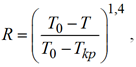(7)
при пониженных температурах, вплоть до температуры застывания. При T ≤ Tkp нефть застывает
и kH = 0. При T > T0 принимают R = 0.
Динамические вязкости фаз вычисляются по известным аналитическим формулам (в системе СИ, т. е. T в K0) [1, 2, 12]
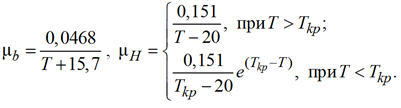(8)
Методы исследования
Уравнение математического баланса можно представить в виде [1, 2]:
(9)
где m – пористость среды.
Эти уравнения заменяются как обычно на другие равносильные им
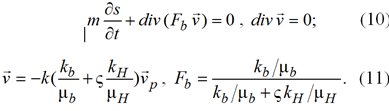
Уравнение (9) можно использовать для вычисления насыщенностей, а (10) для определения поля давления.
Для нахождения температуры можно использовать следующее уравнение [1, 2, 7]:
(12)
где ck – теплоемкость; Hk – мощность пропластка; qk – тепловой поток, уходящий из пропластка с номером k.
Удельная теплоемкость на единицу площади k-го пропластка вычисляется с присоединением глинистых перемычек [1, 2, 7]:
(13)
Изменение температуры происходит за счет переноса тепла конвекцией при фильтрации жидкости и кондуктивной теплопередачи от соседних пропластков
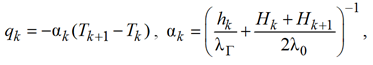(14)
где λ – коэффициент теплопередачи.
Уравнения теплопроводности для окружающих горных пород имеет вид:
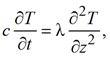(15)
где координата z перпендикулярна напластованию, под с подразумевается объемная теплоемкость кровли или подошвы.
При площадном вытеснении выражение для поля давления (10) удовлетворяет эллиптическому уравнению:
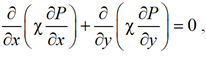, (16)
где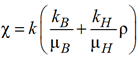 
, k – проницаемость; ρ – структурный множитель.
При разностной аппроксимации уравнений (10), (16) необходимо учитывать сопротивление нагнетательной и добывающей скважины.
При заданных давлениях на контурах скважин их дебиты заранее неизвестны [1, 2, 6, 13, 14].
Вязкость, относительные проницаемости являются функциями координат (x, y) и c.
В прямоугольнике периодов вводится равномерная прямоугольная сетка:
.
Согласно закону сложения гидроводностей при последовательном соединении имеем:
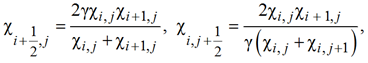(17)
где 
– гидропроводность звеньев.
Формула (17) учитывает геометрию сетки веденным коэффициентом 
(при g = 1 имеем квадратную сетку).
Условие материального баланса без учета узлов можно записать в виде:
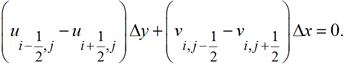(18)
При Dx = Dy, используя формулу (16), имеем для определения давления в обычном узле [1, 2, 12]:
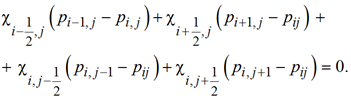(19)
Если в узле (i, j + 1) оказываются добывающие скважины, то вместо (19) имеем:
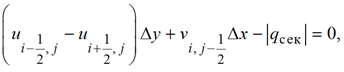(20)
где qсек выражается через разность давлений и гидропроводность.
В окрестностях вокруг нагнетательной скважины величина скорости будет:
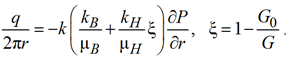. (21)
Из выражения (21) для градиента давления имеем:
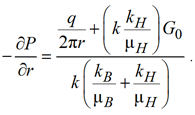. (22)
Интегрируя (22) в пределах от r = Rc до соседних узлов 
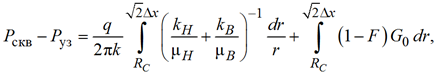(23)
где F – доля воды в потоке для случая, когда структурные свойства не учитываются, перед скачком насыщенности F = 0, а за скачком насыщенности она близка к 1. Введем обозначение
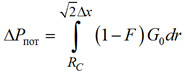. (24)
В кольцевой ячейке, где находится фронт вытеснения, скачок насыщенности определяется из условия максимума дроби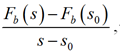 
, где Fb – доля воды в потоке с учетом аномальных свойств нефти. Движение скачка насыщенности определяется по формуле
. (25)
Формула (23) позволяет явно вычислить дебит скважины на единицу мощности:
(26)
где Pнаг соответствует давлению в узле (1, 1), т. е. за начало координат принята точка (1, 1).
Результаты и обсуждение
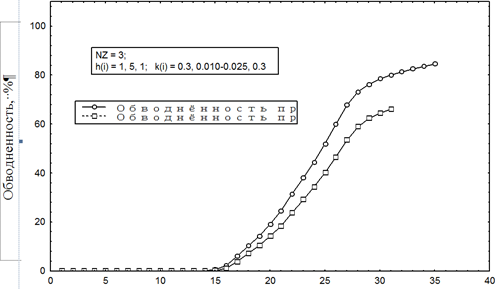
Расчеты характеристик термозаводнения для трехслойного пласта с учетом начального градиента сдвига, выпадения парафина и межслойного теплообмена по изложенным выше методам приведены ниже в таблице и изображены на рисунке.
Результаты вытеснения парафинистой нефти водой
Results of displacement of paraffin oil by water
|
Гoд |
Нефтеотдача B, % |
Обводнение, % |
Расход нефти, м3 |
Закачено воды, т |
Добыто нефти, т |
Прокачен объем |
|
|
0,23 |
0,2 |
0 |
13,0 |
1 353,0 |
1 012,0 |
0,001 |
|
|
К = 2 застыл |
|
||||||
|
1,0 |
0,8 |
0 |
11,1 |
4 702,0 |
3 523,0 |
0,005 |
|
|
Пpoплacток k = 2 зaкупopилcя |
|
||||||
|
2,0 |
1,4 |
0 |
10,3 |
8 606,0 |
6 461,0 |
0,009 |
|
|
3,0 |
2,0 |
0 |
9,5 |
12 277,0 |
9 229,0 |
0,013 |
|
|
4,0 |
2,6 |
0 |
9,2 |
15 810,0 |
11 896,0 |
0,016 |
|
|
5,0 |
3,1 |
0 |
9,3 |
19 255,0 |
14 500,0 |
0,020 |
|
|
6,0 |
3,7 |
0 |
8,9 |
22 633,0 |
17 054,0 |
0,023 |
|
|
7,0 |
4,2 |
0 |
8,8 |
25 960,0 |
19 571,0 |
0,027 |
|
|
8,0 |
4,8 |
0 |
8,7 |
29 244,0 |
22 056,0 |
0,030 |
|
|
9,0 |
5,3 |
0 |
8,7 |
32 492,0 |
24 514,0 |
0,033 |
|
|
10,0 |
5,8 |
0 |
8,6 |
35 707,0 |
26 948,0 |
0,037 |
|
|
11,0 |
6,3 |
0 |
8,6 |
38 894,0 |
29 360,0 |
0,040 |
|
|
12,0 |
6,9 |
0 |
8,5 |
42 055,0 |
31 752,0 |
0,043 |
|
|
13,0 |
7,4 |
0 |
8,4 |
45 191,0 |
34 126,0 |
0,047 |
|
|
14,0 |
7,9 |
0,1 |
8,3 |
48 300,0 |
36 484,0 |
0,050 |
|
|
20,0 |
12,2 |
14,2 |
7,6 |
75 527,0 |
56 489,0 |
0,078 |
|
|
25,0 |
14,1 |
40,2 |
5,0 |
31 527,0 |
65 505,0 |
0,095 |
|
Время, год
Зависимость обводненности низкопроницаемого пласта от времени для трехслойного пласта
при различных режимах вытеснения
Dependence of the a low-permeable formation water content on time for a three-layer formation
under various displacement modes
Заключение
Рассмотрены случаи, когда высокопроницаемые пропластки окружают низкопроницаемый, и наоборот. Расчеты проведены для трехрядной системы расстановки скважин при размерах пласта (элемент симметрии) 800 × 480 м и шаге сетки 80 м. Температура нагнетаемой воды варьировалась.
Рассмотрены случаи холодного заводнения температуры 15 °С, при пластовой температуре, а также нагнетания горячей воды при Т = 90 °С в течение нескольких лет с последующим переходом на нагнетание холодной воды при Т = 15 °С.
Исследования показывают, что вытеснение вязкопластичной нефти путем предварительного создания оторочки горячей воды повышает нефтеотдачу.
1. Ахмедов С. А. Фильтрация многофазных многокомпонентных смесей при разработке нефтяных месторождений: дис. … д-ра техн. наук. Махачкала, 2000. 261 с.
2. Алишаев М. Г., Розенберг М. Д., Теслюк Е. В. Неизотермическая фильтрация при разработке нефтяных месторождений. М.: Недра, 1985. 271 с.
3. Ахмедов С. А., Ахмедова З. Х., Ахмедова Х. Г. Расчет температурного поля в задачах вытеснения парафинистой нефти водой в многослойном пласте // Вестн. Астрахан. гос. техн. ун-та. 2017. № 1 (63). С. 7-14.
4. Алтунина Л. К., Кувшинов В. А. Физико-химическое методы увеличения нефтеотдачи пластов // Вестн. Санкт-Петербург. ун-та. Сер.: 4. 2013. Вып. 2. С. 46-49.
5. Малюков В. П. Физические процессы циклического паротеплового воздействия при разработке месторождений высоковязкой нефти // Гор. информ.-аналит. бюл. 2016. № 12. С. 260-269.
6. Теслюк Е. В. Вопросы неизотермической филь-трации в теории и практике разработки нефтяных месторождений. М.: Недра, 1970. 256 с.
7. Ахмедов С. А., Ахмедова З. Х., Ахмедова Х. Г. Влияние слоистой неоднородности пласта на показатели разработки при неизотермическом вытеснении парафинистой нефти водой // Вестн. Астрахан. гос. техн. ун-та. 2016. № 1 (61). С. 14-21.
8. Малофеев Г. Е., Мирсаетов О. М., Чоловская И. Д. Нагнетание в пласт теплоносителей для интенсификации добычи нефти и увеличения нефтеотдачи. Ижевск: НИЦ «Регулярная и хаотическая динамика», 2008. 224 c.
9. Кузнецова В. М., Петров Д. И. Изменение качества нефти в зависимости от содержания парафинов, смол и асфальтенов // Молодой ученый. 2017. № 4 (138). С. 103-105.
10. Ахмедов С. А., Ахмедова З. Х. Математическое моделирование задачи вытеснения парафинистой нефти водой с учетом технологии нагнетания воды // Вестн. Дагестан. гос. ун-та. Сер. 1: Естественные науки. 2019. Т. 34, Вып. 1. С. 32-37.
11. Малюков В. П., Алибеков М. Э. Инновационные технологии добычи нефти на месторождениях сверхвязких нефтей Татарстана // Вестн. РУДН. 2015. С. 102-107.
12. Ахмедов С. А. Термогидродинамичесикие расчеты задачи неизотермического вытеснения вытеснения вязкопластичной нефти водой в многослойном пласте // Вестн. Дагестан. гос. ун-та. 2005. Вып. 1. С. 38-42.
13. Алишаев М. Г., Ахмедов С. А. Неизотермическое вытеснение парафинистой нефти водой для трехрядной системы расстановки скважин с учетом межслойного теплообмена // Нефт. хоз-во. 1998. № 11. С. 31-32.
14. Ахмедов С. А., Алисултанов Р. М. Компьютерное моделирование задачи вытеснения вязкопластичной нефти водой в многослойном пласте // Нефт. хоз-во. 1999. № 12. С. 38-41.
