Russian Federation
With the discovery of heavy oil deposits, great attention has been paid to the development of oil fields using thermal methods of influencing oil formations. Theoretical studies of reservoir hydrodynamics, as well as temperature fields in multilayer formations, were stimulated with the advent of modern computers and personal computers. Thanks to the mathematical description, hydrodynamic calculations of the displacement of viscoplastic oil by water with abnormal properties became possible. In the case of displacement of high-viscosity and paraffinic oils by cold water in multi-layer formations, paraffin deposition and blockage of weakly permeable formations occur, as a result of the advanced displacement of oil through layers with high permeability. The results of the conducted research show that the creation of a hot water delay at different stages of the development of deposits of high-viscosity paraffin oil improves the development rate, increases the oil recovery coefficient.
deposits of multiphase multicomponent mixture, viscoplastic oil, oil fields
Введение
Запасы тяжелой вязкопластичной нефти в мире примерно в 5 раз превышает остаточных извлекаемых запасов легких нефтей малой и средней вязкости. В последние годы разработке тяжелых нефтей уделяется все большее внимание, особенно в северных районах нашей страны. Месторождения: Ромашкинское, Узеньское, Астраханское, Ярегское, Усинское, Ашальтинкое и др. [1–5] содержат значительное количество парафина, смол и асфальтенов. На месторождениях с парафинистой нефтью небольшое снижение пластовой температуры приводит к осаждению парафина и закупорке поровых каналов. Нефть становится дисперсной средой и может привести к прекращению фильтрации. Необходимо тепловое воздействие на пласт путем закачки теплой воды или горением.
Постановка задачи
Для математического моделирования движения неньютоновской жидкости предлагаются различные модификации закона Дарси. Для месторождений, где с понижением температуры (меньше 20 ºС), нефть приобретает вязкопластичные свойства, предложена модель, где фильтрация считается невозможной, а при больших градиентах фильтрации описывается законом Дарси:
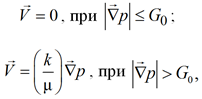(1)
где G0 – начальный градиент, который зависит от вязкости µ проницаемости k среды и температуры [1].
Зависимость градиента сдвига G0 от проницаемости рассмотрена в работах [2, 6]. Для пористой среды радиус капилляра обычно заменяют на и вводят множитель a, учитывающий связь эффективного радиуса наиболее крупных пор с проницаемостью:
(2)
где τ0 – предельное напряжение сдвига жидкости.
Для оценки значений начального градиента сдвига по предельному напряжению сдвига обычно значение коэффициента a принимают в пределах от 0,017 до 0,065.
Исследования авторов подтверждают, что разработка месторождений высоковязких и парафинистых нефтей с экономической и технологической точки зрения наиболее эффективным является закачка горячей воды и пара [1–11].
Закачка горячей воды влияет на текущую добычу нефти и конечную нефтеотдачу. Низкопроницаемые пропластки могут отключиться в двух случаях: если перепад давления мал и недостаточен для преодоления градиента сдвига; если вокруг нагнетательной скважины пласт остудился еще до прохождения фронта вытеснения до температуры застывания нефти.
Математическое моделирование
В общепринятых обозначениях для скоростей фильтрации фаз принимается
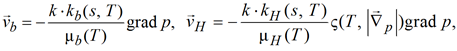(3)
где 
– скорость течения воды; kb(s, T) – проницаемость; s – насыщенность; T – температура; µb(T) – вязкость; 
– скорость течения нефти; kH(s, T) – проницаемость; µH(T) – вязкость нефти; причем структурный множитель ς в программных реализациях имеет вид [1, 2]:
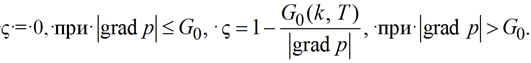(4)
В случае появления критических точек нулевой скорости появляется погрешность счета, обусловленное дисбалансом при девятиточечной и рядной системах. Для учета данного обстоятельства формулу для структурного множителя можно представить в виде [1, 2]:
(5)
где α0 – значение структурного множителя.
Относительные фазовые проницаемости нефти и воды представим в виде [1, 2]:
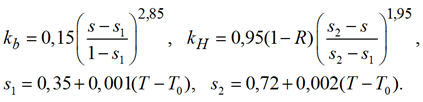(6)
Величина R = 0, если температура больше чем пластовая температура T0, вычисляемая по формуле
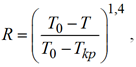(7)
при пониженных температурах, вплоть до температуры застывания. При T ≤ Tkp нефть застывает
и kH = 0. При T > T0 принимают R = 0.
Динамические вязкости фаз вычисляются по известным аналитическим формулам (в системе СИ, т. е. T в K0) [1, 2, 12]
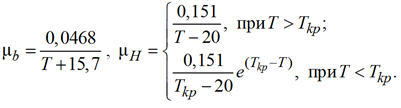(8)
Методы исследования
Уравнение математического баланса можно представить в виде [1, 2]:
(9)
где m – пористость среды.
Эти уравнения заменяются как обычно на другие равносильные им
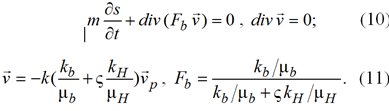
Уравнение (9) можно использовать для вычисления насыщенностей, а (10) для определения поля давления.
Для нахождения температуры можно использовать следующее уравнение [1, 2, 7]:
(12)
где ck – теплоемкость; Hk – мощность пропластка; qk – тепловой поток, уходящий из пропластка с номером k.
Удельная теплоемкость на единицу площади k-го пропластка вычисляется с присоединением глинистых перемычек [1, 2, 7]:
(13)
Изменение температуры происходит за счет переноса тепла конвекцией при фильтрации жидкости и кондуктивной теплопередачи от соседних пропластков
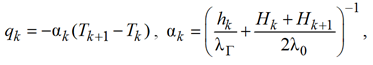(14)
где λ – коэффициент теплопередачи.
Уравнения теплопроводности для окружающих горных пород имеет вид:
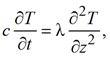(15)
где координата z перпендикулярна напластованию, под с подразумевается объемная теплоемкость кровли или подошвы.
При площадном вытеснении выражение для поля давления (10) удовлетворяет эллиптическому уравнению:
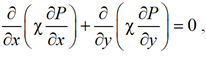, (16)
где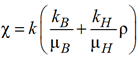 
, k – проницаемость; ρ – структурный множитель.
При разностной аппроксимации уравнений (10), (16) необходимо учитывать сопротивление нагнетательной и добывающей скважины.
При заданных давлениях на контурах скважин их дебиты заранее неизвестны [1, 2, 6, 13, 14].
Вязкость, относительные проницаемости являются функциями координат (x, y) и c.
В прямоугольнике периодов вводится равномерная прямоугольная сетка:
.
Согласно закону сложения гидроводностей при последовательном соединении имеем:
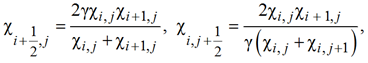(17)
где 
– гидропроводность звеньев.
Формула (17) учитывает геометрию сетки веденным коэффициентом 
(при g = 1 имеем квадратную сетку).
Условие материального баланса без учета узлов можно записать в виде:
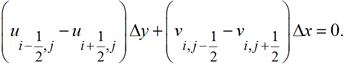(18)
При Dx = Dy, используя формулу (16), имеем для определения давления в обычном узле [1, 2, 12]:
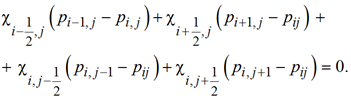(19)
Если в узле (i, j + 1) оказываются добывающие скважины, то вместо (19) имеем:
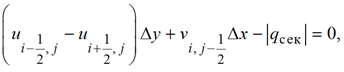(20)
где qсек выражается через разность давлений и гидропроводность.
В окрестностях вокруг нагнетательной скважины величина скорости будет:
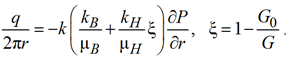. (21)
Из выражения (21) для градиента давления имеем:
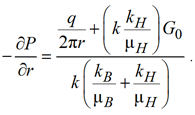. (22)
Интегрируя (22) в пределах от r = Rc до соседних узлов 
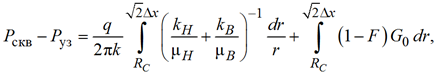(23)
где F – доля воды в потоке для случая, когда структурные свойства не учитываются, перед скачком насыщенности F = 0, а за скачком насыщенности она близка к 1. Введем обозначение
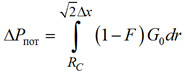. (24)
В кольцевой ячейке, где находится фронт вытеснения, скачок насыщенности определяется из условия максимума дроби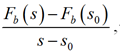 
, где Fb – доля воды в потоке с учетом аномальных свойств нефти. Движение скачка насыщенности определяется по формуле
. (25)
Формула (23) позволяет явно вычислить дебит скважины на единицу мощности:
(26)
где Pнаг соответствует давлению в узле (1, 1), т. е. за начало координат принята точка (1, 1).
Результаты и обсуждение
Расчеты характеристик термозаводнения для трехслойного пласта с учетом начального градиента сдвига, выпадения парафина и межслойного теплообмена по изложенным выше методам приведены ниже в таблице и изображены на рисунке.
Результаты вытеснения парафинистой нефти водой
Results of displacement of paraffin oil by water
|
Гoд |
Нефтеотдача B, % |
Обводнение, % |
Расход нефти, м3 |
Закачено воды, т |
Добыто нефти, т |
Прокачен объем |
|
|
0,23 |
0,2 |
0 |
13,0 |
1 353,0 |
1 012,0 |
0,001 |
|
|
К = 2 застыл |
|
||||||
|
1,0 |
0,8 |
0 |
11,1 |
4 702,0 |
3 523,0 |
0,005 |
|
|
Пpoплacток k = 2 зaкупopилcя |
|
||||||
|
2,0 |
1,4 |
0 |
10,3 |
8 606,0 |
6 461,0 |
0,009 |
|
|
3,0 |
2,0 |
0 |
9,5 |
12 277,0 |
9 229,0 |
0,013 |
|
|
4,0 |
2,6 |
0 |
9,2 |
15 810,0 |
11 896,0 |
0,016 |
|
|
5,0 |
3,1 |
0 |
9,3 |
19 255,0 |
14 500,0 |
0,020 |
|
|
6,0 |
3,7 |
0 |
8,9 |
22 633,0 |
17 054,0 |
0,023 |
|
|
7,0 |
4,2 |
0 |
8,8 |
25 960,0 |
19 571,0 |
0,027 |
|
|
8,0 |
4,8 |
0 |
8,7 |
29 244,0 |
22 056,0 |
0,030 |
|
|
9,0 |
5,3 |
0 |
8,7 |
32 492,0 |
24 514,0 |
0,033 |
|
|
10,0 |
5,8 |
0 |
8,6 |
35 707,0 |
26 948,0 |
0,037 |
|
|
11,0 |
6,3 |
0 |
8,6 |
38 894,0 |
29 360,0 |
0,040 |
|
|
12,0 |
6,9 |
0 |
8,5 |
42 055,0 |
31 752,0 |
0,043 |
|
|
13,0 |
7,4 |
0 |
8,4 |
45 191,0 |
34 126,0 |
0,047 |
|
|
14,0 |
7,9 |
0,1 |
8,3 |
48 300,0 |
36 484,0 |
0,050 |
|
|
20,0 |
12,2 |
14,2 |
7,6 |
75 527,0 |
56 489,0 |
0,078 |
|
|
25,0 |
14,1 |
40,2 |
5,0 |
31 527,0 |
65 505,0 |
0,095 |
|
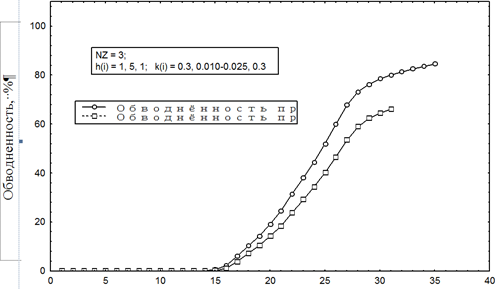
Время, год
Зависимость обводненности низкопроницаемого пласта от времени для трехслойного пласта
при различных режимах вытеснения
Dependence of the a low-permeable formation water content on time for a three-layer formation
under various displacement modes
Заключение
Рассмотрены случаи, когда высокопроницаемые пропластки окружают низкопроницаемый, и наоборот. Расчеты проведены для трехрядной системы расстановки скважин при размерах пласта (элемент симметрии) 800 × 480 м и шаге сетки 80 м. Температура нагнетаемой воды варьировалась.
Рассмотрены случаи холодного заводнения температуры 15 °С, при пластовой температуре, а также нагнетания горячей воды при Т = 90 °С в течение нескольких лет с последующим переходом на нагнетание холодной воды при Т = 15 °С.
Исследования показывают, что вытеснение вязкопластичной нефти путем предварительного создания оторочки горячей воды повышает нефтеотдачу.
1. Akhmedov S. A. Fil'tratsiia mnogofaznykh mnogokomponentnykh smesei pri razrabotke neftianykh mestorozhdenii: dis. … d-ra tekhn. nauk [Filtration of multiphase multicomponent mixtures in the development of oil fields: dis. ... doctor of technical]. Makhachkala, 2000. 261 p.
2. Alishaev M. G., Rozenberg M. D., Tesliuk E. V. Neizotermicheskaia fil'tratsiia pri razrabotke neftianykh mestorozhdenii [Non-isothermal filtration in the development of oil fields]. Moscow, Nedra Publ., 1985. 271 p.
3. Akhmedov S. A., Akhmedova Z. Kh., Akhmedova Kh. G. Raschet temperaturnogo polia v zadachakh vytesneniia parafinistoi nefti vodoi v mnogosloinom plaste [Calculation of the temperature field in problems of displacement of paraffin oil by water in a multilayer formation]. Vestnik Astrakhanskogo gosudarstvennogo tekhnicheskogo universiteta, 2017, no. 1 (63), pp. 7-14.
4. Altunina L. K., Kuvshinov V. A. Fiziko-khimicheskoe metody uvelicheniia nefteotdachi plastov [Physico-chemical methods of increasing oil recovery]. Vestnik Sankt-Peterburgskogo universiteta. Seriia: 4, 2013, vol. 2, pp. 46-49.
5. Maliukov V. P. Fizicheskie protsessy tsiklicheskogo paroteplovogo vozdeistviia pri razrabotke mestorozhdenii vysokoviazkoi nefti [Physical processes of cyclic steam-thermal effects in the development of high-viscosity oil fields]. Gornyi informatsionno-analiticheskoi biulleten', 2016, no. 12, pp. 260-269.
6. Tesliuk E. V. Voprosy neizotermicheskoi fil'tratsii v teorii i praktike razrabotki neftianykh mestorozhdenii [Is-sues of non-isothermal filtration in the theory and practice of oil field development]. Moscow, Nedra Publ., 1970. 256 p.
7. Akhmedov S. A., Akhmedova Z. Kh., Akhmedova Kh. G. Vliianie sloistoi neodnorodnosti plasta na pokazateli razrabotki pri neizotermicheskom vytesnenii parafinistoi nefti vodoi [The effect of layered heterogeneity of the formation on the development indicators during non-isothermal displacement of paraffin oil by water]. Vestnik Astrakhanskogo gosudarstvennogo tekhnicheskogo universiteta, 2016, no. 1 (61), pp. 14-21.
8. Malofeev G. E., Mirsaetov O. M., Cholovskaia I. D. Nagnetanie v plast teplonositelei dlia intensifikatsii dobychi nefti i uvelicheniia nefteotdachi [Injection of heat carriers into the reservoir to intensify oil production and increase oil recovery]. Izhevsk, NITs. Reguliarnaia i khaoticheskaia dinamika, 2008. 224 p.
9. Kuznetsova V. M., Petrov D. I. Izmenenie kachestva nefti v zavisimosti ot soderzhaniia parafinov, smol i asfal'tenov [Oil quality changes depending on the content of paraffins, resins and asphaltenes]. Molodoi uchenyi, 2017, no. 4 (138), pp. 103-105.
10. Akhmedov S. A., Akhmedova Z. Kh. Matematich-eskoe modelirovanie zadachi vytesneniia parafinistoi nefti vodoi s uchetom tekhnologii nagnetaniia vody [Mathemati-cal modeling of the problem of displacement of paraffinic oil with water taking into account the water injection technology]. Vestnik Dagestanskogo gosudarstvennogo universiteta. Seriia: 1. Estestvennye nauki, 2019, iss. 34, vol. 1, pp. 32-37.
11. Maliukov V. P., Alibekov M. E. Innovatsionnye tekhnologii dobychi nefti na mestorozhdeniiakh sverkh-viazkikh neftei Tatarstana [Innovative technologies of oil production in the fields of ultra-viscous oils of Tatarstan]. Vestnik RUDN, 2015, pp. 102-107.
12. Akhmedov S. A. Termogidrodinamichesikie raschety zadachi neizotermicheskogo vytesneniia vytesneniia viazkoplastichnoi nefti vodoi v mnogosloinom plaste [Thermohydrodynamic calculations of the problem of non-isothermal displacement of the displacement of viscoplastic oil by water in a multilayer formation]. Vestnik Dagestanskogo gosudarstvennogo universiteta, 2005, vol. 1, pp. 38-42.
13. Alishaev M. G., Akhmedov S. A. Neizotermicheskoe vytesnenie parafinistoi nefti vodoi dlia trekhriadnoi sistemy rasstanovki skvazhin s uchetom mezhsloinogo teploobmena [Non-isothermal displacement of paraffin oil with water for a three-row well placement system taking into account inter-layer heat exchange]. Neftianoe khoziaistvo, 1998, no. 11, pp. 31-32.
14. Akhmedov S. A., Alisultanov R. M. Komp'iuternoe modelirovanie zadachi vytesneniia viazkoplastichnoi nefti vodoi v mnogosloinom plaste [Computer simulation of the problem of displacement of viscoplastic oil by water in a multilayer formation]. Neftianoe khoziaistvo, 1999, no. 12, pp. 38-41.
