Разработан вероятностный подход к учету влияния ограниченного периода ликвидности на объем продаж товара. Основу подхода составляет предположение о случайном характере экономических факторов, определяющих динамику продаж товара: моментов производства, моментов покупок, периода ликвидности, количества товара и количества потребителей. Найдены аналитические выражения для функции вероятности и математического ожидания временной зависимости количества проданного товара в двух случаях: без учета и с учетом моментов производства товара. Проведено численное моделирование динамики математического ожидания количества проданного товара. Показано, что по мере роста числа покупателей рынок товара становится все более управляемым, т. к. реальная динамика количества проданного товара и динамика математического ожидания этого количества перестают отличаться друг от друга. Определены общие закономерности совместного влияния параметров вероятностных законов распределения пяти упомянутых выше экономических факторов на величину и динамику объема продаж товара. В рамках предложенной вероятностной модели найдена временная зависимость, аппроксимирующая реальную динамику продаж автомобилей «Лада Веста» на российском рынке в период с октября 2015 г. по май 2023 г.
ликвидность, период ликвидности, моменты изготовления товара, моменты покупательской активности, объем продаж, производящая функция вероятностей, плотность распределения вероятностей, математическое ожидание
Введение
Ликвидность – это такая характеристика актива, которая показывает, насколько быстро он может быть продан по рыночной цене [1]. Ликвидность является очень широким понятием в экономике, которое применяется не только к активам, но и к предприятиям, банкам и целым рынкам [1, 2]. По этой причине существует много количественных показателей, которые являются мерой ликвидности. Например, ликвидность предприятия оценивают через показатель текущей ликвидности, равный отношению оборотных активов предприятия к краткосрочным обязательствам [1, 2].
Подавляющее большинство мер ликвидности не содержат явно временные параметры, имеющие отношение к продаже актива, и поэтому оценивают скорость его продажи опосредованно, делая само понятие ликвидности актива не вполне прозрачным. Опыт использования таких мер ликвидности на фондовых рынках показал, что они неудовлетворительно оценивают ликвидность актива в условиях быстро меняющейся экономической ситуации на рынке [3]. Поэтому на фондовых рынках было предложено использовать показатели ликвидности, основанные на понятии времени торговли (trade-time measures of liquidity), которые надежны и точны даже в случае стрессовых изменений экономической конъюнктуры [3].
Однако, независимо от способа определения, существующие показатели ликвидности не учитывают влияние на скорость продажи актива (товар) временных параметров, определяющих процесс производства товара и покупательскую активность потребителей. Для количественной оценки ликвидности товара наиболее важными временными характеристиками являются моменты времени изготовления товара, моменты покупательской активности потребителей и период ликвидности товара. Моменты покупательской активности – это моменты времени, в которые потребители проявляют интерес к покупке товара, а период ликвидности – это такой промежуток времени, отсчитываемый от начала продаж товара, в течение которого потребитель сохраняет интерес к покупке этого товара. По истечении периода ликвидности потребитель полагает, что товар утрачивает покупательскую ценность, и не приобретает его. Период ликвидности определяется не только свойствами самого товара, но и представлениями потребителей об изменении потребительских качеств товара с течением времени.
Без учета этих временных параметров, связанных с процессами производства и покупки товара, корректное построение количественной меры ликвидности товара невозможно. А поскольку моменты времени изготовления товара, моменты покупательской активности и периоды ликвидности товара являются случайными величинами, корректно оценить с их помощью ликвидность товара можно только в рамках вероятностной модели.
Наилучшей прямой оценкой ликвидности товара является динамика объема его продаж, потому что она непосредственно показывает, как быстро и в каком количестве товар продается в различные моменты времени. Целью настоящей работы является построение вероятностной модели, определяющей зависимость от времени количества проданного товара, при условии, что процессы производства и покупки товара регулируются пятью случайными величинами: моментами изготовления товара, моментами покупательской активности потребителей, периодами ликвидности товара, а также количеством товара и количеством потребителей. По нашим сведениям, такое количественное определение ликвидности товара дается впервые.
Простейшая вероятностная модель динамики объема продаж товара
Рассмотрим простейшую экономическую модель: на некотором рынке появляется товар, имеющий ограниченный период ликвидности, к покупке которого проявляют интерес N потребителей. Будем считать, что каждый потребитель обладает неограниченной покупательской способностью и стремится приобрести лишь одну единицу товара. При этих предположениях модель продажи товара не усложнена учетом таких экономических факторов, как покупательская способность потребителей, торговая наценка и издержки, вызванные продажей единицы товара, что позволяет установить характер влияния именно периода ликвидности товара на объемы его продаж. Для простоты примем, что весь товар, имеющийся на рынке, был изготовлен и поступил в продажу в один и тот же момент времени t = 0.
Индивидуальные представления потребителей о покупательской ценности товара на момент покупки различны: кто-то готов купить слегка просроченный товар, а кто-то не купит этот товар и за несколько дней до истечения срока его годности. По этой причине для разных потребителей, пытающихся купить один и тот же товар в одно и то же время, период его ликвидности будет различен. Обозначим через τj период ликвидности товара, актуальный для j-го потребителя, который в момент времени tj на рассматриваемом рынке совершает покупку единицы этого товара. Здесь и далее j ∈ {1, 2, …, N}. Приобретаемый товар обладает покупательской ценностью для j-го потребителя, только если в момент покупки период ликвидности еще не истек: tj ≤ τj. Следовательно, при выполнении неравенства tj ≤ τj j-й потребитель купит товар в момент времени tj, а общее количество товара, которое будет продано на рынке в течение промежутка времени [0; t], составит
где t – текущий момент времени; H(A) – индикатор появления случайного события A: H(A) = 1, если событие A произошло, и H(A) = 0, если событие A не произошло.
Поскольку N, tj и τj являются случайными величинами, мгновенное значение количества проданного товара Q(t) также представляет собой случайную величину. Дадим полное вероятностное описание дискретной случайной величины Q(t) – найдем для нее производящую функцию вероятностей [4]:
1. Количество N потребителей на рынке не зависит ни от моментов t1, t2, …, tN, в которые потребители пытаются купить товар, ни от периодов
τ1, τ2, …, τN ликвидности товара. Известно вероятностное описание дискретной случайной величины N в виде производящей функции вероятностей
2. Моменты t1, t2, …, tN, в которые потребители пытаются купить товар, не зависят от периодов τ1, τ2, …, τN ликвидности товара. Потребители совершают покупки независимо друг от друга, а их множество на рынке является однородным. Отсюда следует, что непрерывные случайные величины t1, t2, …, tN попарно независимы и одинаково распределены. Известна их плотность распределения вероятностей φc(x).
3. Периоды τ1, τ2, …, τN ликвидности товара также являются попарно независимыми, одинаково распределенными непрерывными случайными величинами с известной плотностью распределения вероятностей φτ(x).
Учитывая сделанные предположения, с помощью (1) нетрудно получить следующее аналитическое выражение для производящей функции вероятностей количества товара Q(t), проданного на рынке в течение промежутка времени [0; t]:
Производная r-го порядка по переменной z от функции GQ(z, t) при z = 1 равна факториальному моменту r-го порядка количества Q(t) проданного товара [4]:
где
где 
– математическое ожидание количества потребителей на рынке.
Анализ формулы (4) показывает, что динамика среднего значения количества товара, проданного на рынке к моменту времени t, представляет собой неубывающую функцию, графиком которой является кривая насыщения: 
монотонно возрастает от значения 
при t = 0 до значения 
а знак равенства достигается только для товара с неограниченным периодом ликвидности. Проиллюстрируем это на примере.
Пусть t1, t2, …, tN и τ1, τ2, …, τN имеют гамма-распределение [4]
,(5)
где αc/τ и βc/τ – параметры формы и масштаба соответственно; Γ(αc/τ) – гамма-функция [5]. Плотности распределения вероятностей (5) моделируют широкий спектр экономических ситуаций на рынке. При αc ≤ 1 основная масса потребителей оказывается на рынке для покупки товара в первые моменты времени после старта продаж. В этом случае потребители давно ожидали появления товара на рынке и стремятся купить его как можно быстрее. Если αc > 1, то потребители проявляют интерес к покупке товара с некоторой задержкой, которая тем больше, чем больше значение αc. Такое поведение потребителей на рынке может быть связано с тем, что им незнакомы потребительские качества товара, например, из-за недостаточной предпродажной рекламы товара. Поэтому количество попыток купить товар нарастает постепенно по мере того, как все большее число потребителей его приобретают, достигает максимума в момент времени 
, а затем снова идет на спад. Аналогично, при ατ ≤ 1 практически все потребители считают, что период ликвидности товара очень мал, стремится к нулю, а при ατ > 1 они в основном полагают, что период ликвидности товара мало отличается от 
. Следовательно, в модели (5) пик покупательской активности потребителей приходится на момент времени 
,
а наиболее вероятное значение периода ликвидности товара, по мнению потребителей, равно 
.
Подстановка (5) в (4) приводит к следующей формуле для :
(6)
где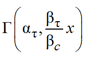 
– верхняя неполная гамма-функция. Максимально возможное значение среднего объема продаж получается из (6) при t → ∞:
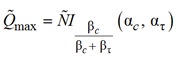(7)
где 
– регуляризованная неполная бета-функция [5]. Свойства регуляризованной
неполной бета-функции таковы, что значение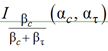 
практически не отличается от максимально возможного значения, равного единице, если выполняется неравенство 
[5]. Но поскольку для гамма-распределений (5) 
и 
примерно равно своему наибольшему значению 
, только если в среднем потребители пытаются купить товар в моменты времени намного меньшие, чем средний период ликвидности товара. В частности, это произойдет, если период ликвидности будет бесконечно большим.
Таким образом, из (6) и (7) следует, что средний объем продаж товара на рынке тем больше, чем больше потребителей вовлечено в процесс его покупки и чем больше его средний период ликвидности по сравнению со средним временем покупательской активности потребителей.
Интеграл, входящий в (6), не вычисляется аналитически. Однако его можно найти численно при конкретных значениях параметров гамма-распределений (5). На рис. 1 представлены типичные зависимости среднего количества 
проданного товара от текущего момента времени t, найденные с помощью (6).
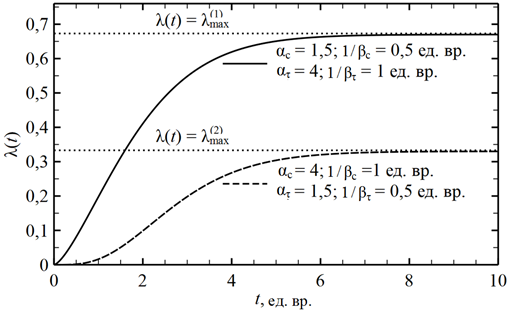
Рис. 1. Рассчитанная по формуле (6) динамика удельного среднего объема продаж λ(t) для двух наборов параметров
гамма-распределений (5) (сплошная и штриховая линии). Горизонтальные пунктирные линии – асимптоты кривых насыщения. Максимально возможные значения удельного среднего объема продаж: 
найдены с помощью формулы (7) при указанных на рисунке значениях параметров гамма-распределений
Fig. 1. The dynamics of the specific average sales volume λ(t) calculated by the formula (6)
for two sets of gamma distribution parameters (5) (solid and dashed lines). Horizontal dotted lines are asymptotes of saturation curves. The maximum possible values of the specific average sales volume:
are found using formula (7) for the values of the parameters of gamma distributions indicated in the figure
Согласно рис. 1, при любых значениях параметров ατ, βτ, αc и βc эти зависимости имеют вид кривых насыщения, обладающих свойством 
. При этом чем больше средний период ликвидности товара ατ / βτ по сравнению со средним временем покупательской активности потребителей αc / βc, тем больше 
и тем быстрее происходит приближение кривой насыщения к своей горизонтальной асимптоте 
. Следовательно, динамика среднего объема продаж, определяемая формулами (6), (7) и изображенная на рис. 1, показывает, что наилучшим состоянием рынка, с точки зрения продавцов и производителей товара, является такое состояние, при котором на рынке много потребителей и все они проявляют покупательскую активность задолго до истечения среднего периода ликвидности товара. Только в этом случае удается продать большее количество товара за меньшее время.
Закон распределения количества проданного товара
Помимо факториальных моментов (3), производящая функция вероятностей (2) позволяет также найти функцию вероятности дискретной случайной величины Q(t):
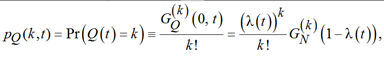(8)
где 
– вероятность того, что случайная величина Q(t) принимает значение, равное k; – производная k-го порядка, вычисленная от производящей функции (2) при z = 0; 
– производная k-го порядка от функции 
, вычисленная при z = 1 – λ(t).
Рассмотрим два частных случая аналитического выражения (8):
1. N – биномиальная случайная величина, равная количеству потребителей, попытавшихся купить товар, среди потребителей, имеющихся на рынке. Если вероятность, с которой отдельный потребитель совершает попытку купить товар, равна p, то 
. Отметим, что при p = 1 производящая функция вероятностей биномиального закона распределения принимает вид 
, который соответствует постоянной случайной величине N, принимающей значение с вероятностью 1: 
. В этом случае количество потребителей на рынке остается неизменным и равным , причем все эти потребители совершают попытку купить товар.
2. N – пуассоновская случайная величина с математическим ожиданием 
.
В этой ситуации количество потребителей на рынке может быть неограниченно большим. Однако их среднее количество является конечной величиной, и все они совершают попытку купить товар.
Как показывают вычисления, в обоих случаях закон распределения случайной величины Q(t) повторяет закон распределения случайной величины N, но с другими параметрами. Если N – биномиальная случайная величина, то и Q(t) имеет биномиальный закон распределения:
(9)
где 
– биномиальные коэффициенты. Если же N – пуассоновская случайная величина, то Q(t) тоже имеет закон распределения Пуассона:
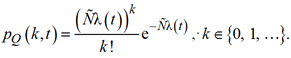(10)
Формулы (8)–(10) позволяют оценить отличия реальной динамики дискретной случайной величины Q(t) от динамики ее математического ожидания 
(см. (4)). Чем меньше это отличие, тем точнее реальная временная зависимость количества проданного товара описывается функцией 
и, следовательно, тем более она предсказуема. На рис. 2 приведены примеры, показывающие величину и характер возможных отличий Q(t) от 
для двух законов распределения (9) и (10) значений количества проданного товара.
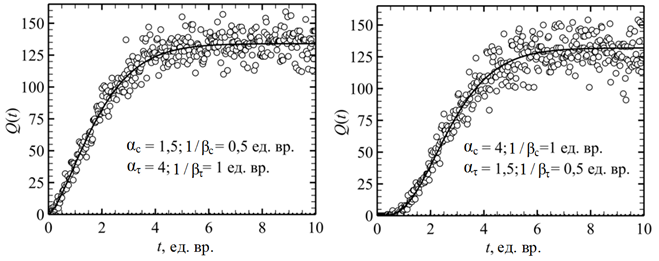
а б
Рис. 2. Значения случайной функции Q(t) (кружки), найденные при 
для двух законов распределения
этих значений: а – биномиальный закон распределения (9) при p = 0,5; б – закон распределения Пуассона (10).
В обоих случаях динамика математического ожидания Q(t) (сплошные линии) была рассчитана по формуле (6)
для тех же наборов параметров гамма-распределений (5), что и на рис. 1
Fig. 2. The values of the random function Q(t) (circles) found 
for two distribution laws of these values:
a – binomial distribution law (9) at p = 0.5; б – Poisson distribution law (10).
In both cases, the dynamics of the mathematical expectation Q(t) (solid lines)
was calculated by the formula (6) for the same sets of parameters of gamma distributions (5) as in Fig. 1
Можно показать в общем виде, что для этих законов распределения отношение среднеквадратического отклонения Q(t) от к математическому ожиданию 
: обратно пропорционально 
. Это значит, что с ростом количества покупателей отклонение Q(t) от уменьшается. Таким образом, прогнозирование динамики объема продаж товара на основе динамики среднего объема продаж является тем более точным, чем больше потребителей вовлечено в процесс покупки товара.
Увеличение количества покупателей на рынке приносит двойную выгоду продавцам и производителям товара: во-первых, увеличивает количество проданного товара (см. формулы (4), (6), (7)), во-вторых, делает рынок более управляемым. Действительно, для продавца рынок товара будет управляемым, если он сможет предсказуемым образом в своих интересах изменить вид функциональной зависимости Q(t), меняя параметры законов распределения моментов покупательской активности и периодов ликвидности, например параметры гамма-распределений (5). Этого можно достичь, если случайный процесс Q(t) мало отличается от своего математического ожидания , динамика которого абсолютно предсказуема и легко изменяется с помощью параметров, входящих в формулы, подобные (6). При известной функции вероятности случайной величины Q(t) можно определить такое количество покупателей товара 
, при котором относительная погрешность 
на рассматриваемом промежутке времени не будет превышать определенной величины с заданной вероятностью. При этом значении все необходимые продавцу особенности зависимости от времени количества проданного товара, которыми он наделил функцию , будут наблюдаться в реальной динамике дискретной случайной величины Q(t) с нужной продавцу вероятностью и установленной им погрешностью. Необходимо лишь, используя инструменты маркетинга, привлечь на рынок для покупки товара требуемое количество потребителей. Несложные вычисления показывают, что для рис. 2, б (
) относительная погрешность 
в области максимальных продаж (плато кривой насыщения) не превышает 5 % с вероятностью ≈ 0,45, но уже при 
вероятность 5 %-го отличия Q(t) от 
в этой временной области составляет ≈ 0,93.
Вероятностная модель динамики продаж товара, отдельные единицы которого изготовлены в различные моменты времени
В рассмотренной выше простейшей вероятностной модели предполагалось, что весь имеющийся на рынке товар был изготовлен в один момент времени t = 0. Если промежуток времени, на котором исследуется временная зависимость количества проданного товара, достаточно велик, то потребитель может столкнуться с тем, что предлагаемые к покупке однотипные единицы товара имеют разную дату изготовления. В такой ситуации потребитель сделает покупку, только если хотя бы одна единица товара из всех имеющихся на рынке и доступных для покупки этому потребителю была изготовлена в момент времени, меньший момента покупки на величину, не превышающую период ликвидности этой единицы товара. Обобщим предыдущую вероятностную модель на этот более реалистичный случай.
Предположим, что за все время продажи товара на рынок было поставлено Ng его единиц, изготовленных в моменты времени 
. Будем считать, что случайные величины Ng и 
не зависят ни от моментов покупательской активности, ни от периодов ликвидности товара, ни от количества потребителей на рынке, а также являются попарно независимыми. Плотность распределения вероятностей моментов изготовления товара обозначим через φg(x), а производящую функцию вероятностей количества товара на рынке – через Gg(z). При этом за начало отсчета времени t = 0 примем нижнюю границу множества значений случайных величин 
,
m ∈ {1, 2, …, Ng}.
Не все товары из множества 
доступны для покупки j-му потребителю. Часть из них могла быть куплена другими потребителями, проявившими покупательскую активность в моменты времени меньшие, чем tj. Товары, не купленные другими потребителями, могут быть недоступны для покупки j-му потребителю при условии, что реализуются на торговых площадках, которые j-й потребитель не может посетить по тем или иным причинам. Обозначим через Mj подмножество множества 
, состоящее из товаров, доступных для покупки j-му потребителю в момент времени tj. Если в этот момент времени на рынке имеется хотя бы одна единица товара, изготовленная в момент времени 
, попадающий в промежуток ликвидности 
, то j-й потребитель купит одну из таких единиц товара. Таким образом, индикатором покупки j-м потребителем товара является равенство единице функции
.
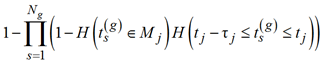При таком условии покупки общее количество товара, проданного на рынке в течение промежутка времени [0; t], равно
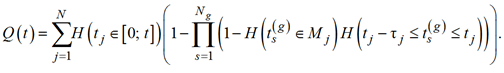(11)
Отметим, что формула (1) является частным случаем (11) при 
и Mj = M для любых j ∈ {1, 2, …, N}.
Точное определение множества Mj является сложным, поскольку предполагает использование не только момента времени tj, в который пытается купить товар j-й потребитель, но и всех моментов покупательской активности меньших, чем tj, а также существенно зависит от того, как распределены по торговым площадкам потребители и товар.
При строгом определении Mj нахождение с помощью (11) закона распределения и математического ожидания количества проданного товара Q(t) практически невозможно. По этой причине далее будем использовать упрощенное определение множества Mj: 
и 
, где 
– вероятность того, что товар, изготовленный в момент времени 
, доступен для покупки j-му потребителю. При этом будем считать, что вероятность 
зависит лишь от двух моментов времени: tj, и равна произведению вероятности того, что изготовленная в момент времени единица товара не продана до момента времени tj, на вероятность 
нахождения этой единицы на торговых площадках, доступных для j-го потребителя: 
.
При этих предположениях, используя свойства случайных величин, входящих в (11), нетрудно получить аналитические выражения для производящей функции вероятностей и математического ожидания количества проданного товара:
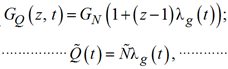(12)
(13)
где λg(t) вычисляется по формуле
где 
– дополнительная интегральная функция распределения вероятностей периода ликвидности; p(x, y) = p1(x, y)p2(x, y).
Производящая функция вероятностей (12) отличается от (2) только тем, что вместо функции λ(t) в (12) входит более сложная функция λg(t). Это значит, что все ранее полученные результаты, относящиеся к закону распределения количества проданного товара (см. (8)–(10)), остаются в силе и в случае товара, различные единицы которого изготовлены в разное время. Необходимо только заменить в формулах (8)–(10) функцию λ(t) на λg(t).
Несмотря на то, что динамика среднего объема продаж, определяемая формулой (13), сложнее, чем динамика, следующая из формулы (4), ее характер остается прежним: с ростом t функция 
монотонно возрастает, стремясь при t → ∞ к асимптотическому значению 
, т. е. графиком временной зависимости (13) является кривая насыщения. Проиллюстрируем это на следующем примере.
Динамика продаж товара, каждая единица которого доступна для покупки любому потребителю почти наверное
Предположим, что вероятность, определяющая доступность отдельных экземпляров товара для потребителя, примерно равна единице: p(x, y) ≈ 1. Существует два вида рынков, реализующих такую экономическую ситуацию:
1. Количество товара на рынке намного больше, чем количество потребителей: Ng ≫ N. Практически все торговые площадки, на которых продается товар, используются потребителями для поиска и покупки товара.
2. Количество товара на рынке примерно равно количеству потребителей: Ng ≈ N, но период ликвидности товара для всех потребителей намного меньше интервала времени между последовательными моментами изготовления товара. При этом интенсивность покупок оказывается близкой к нулю. Доступность торговых площадок для потребителей такая же, как и в первом случае.
Оба рынка характеризуются тем, что каждый потребитель независимо от того, в какой момент времени он проявляет покупательскую активность, выбирает товар практически из всего множества товаров, изготовленных до момента его появления на рынке. Для обоих рынков функция λg(t), входящая в (12) и (13), определяется следующим выражением:
.
Пусть далее производство товара является стационарным пуассоновским процессом. При этом количество товара Ng имеет распределение Пуассона, а моменты изготовления товара 
– равномерное распределение на промежутке времени [0; Tg]:
,
где Tg – жизненный цикл товара; βg – интенсивность производства товара, равная количеству товара, изготавливаемому в единицу времени. В этом случае формула (13) приобретает вид
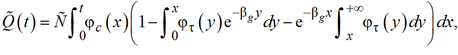(14)
где учтено, что все моменты времени, представляющие интерес для исследования динамики объема продаж, удовлетворяют очевидному неравенству 
.
Предположим, что периоды ликвидности товара имеют показательное распределение:
,
где 
– средний период ликвидности, характерный для данного множества потребителей. При таком законе распределения большинство потребителей на рынке считают, что период ликвидности товара меньше, чем , а вероятность встретить потребителя, который полагает, что период ликвидности намного больше, чем
, экспоненциально мала. Подставив это показательное распределение в (14), получим:
. (15)
Если потребители проявляют наибольший интерес к покупке товара в самые первые моменты времени после его появления на рынке, а затем все реже и реже совершают попытки его купить, то в качестве закона распределения моментов покупательской активности, моделирующего это поведение потребителей, можно, как и в случае с периодами ликвидности, взять показательное распределение
,
где 
– средняя продолжительность потребительского интереса к покупке товара. При этом (15) примет вид
(16)
Графиком временной зависимости (16) при любых значениях параметров 
является кривая насыщения, подобная тем, что изображены на рис. 1. Количество проданного товара никогда не превышает предельного значения 
, которое, как следует из (16), равно
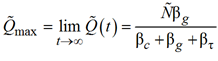(17)
Анализ формулы (17) показывает, что 
достигает своего наибольшего значения 
, при котором, по прошествии достаточно большого времени, каждый потребитель на рынке купит товар только при выполнении неравенства 
. С помощью величины 
, имеющей смысл среднего интервала времени между двумя последовательными моментами изготовления товара, этому неравенству можно придать вид 
. Таким образом, для полного удовлетворения спроса на товар производитель должен так организовать производство, чтобы средний промежуток времени между последовательными моментами изготовления товара был намного меньше, чем половина среднего гармонического величин 
и . Например, если средний период ликвидности товара составляет 1 неделю: τ ̃ = 7 дней, а средняя продолжительность потребительского интереса к покупке товара равна одному дню: c = 1 день, то τ ̃g ≪ 7 / 8 дня. В частности, при
дня (единица товара изготавливается производителем в среднем один раз в час) в рассматриваемом числовом примере потребительский спрос будет удовлетворен не более чем на 95 %,
т. к. из (17) следует, что 
.
Анализ динамики продаж автомобилей семейства моделей «Лада Веста» в России
Рассмотрим еще один важный частный случай вероятностной модели (12), (13), когда вероятность, определяющая доступность товара для потребителя, является константой, намного меньшей единицы: p(x, y) = p0 ≪ 1. Низкая доступность отдельных экземпляров товара для потребителей может быть следствием дефицита товара на рынке, условием появления которого является выполнение неравенства Ng ≪ N. Однако она может реализоваться на рынке и при условии, что Ng ≈ N, если процент недоступных для потребителя торговых площадок и период ликвидности товара настолько большие, что практически весь товар раскупается сразу после поступления на рынок. При p(x, y) = p0 ≪ 1 в (13) можно ограничиться линейным по p0 приближением:
(18)
где, как и в (14), предполагается, что t < Tg, а 
– математическое ожидание количества товара, изготовленного на промежутке времени [0; Tg].
Если производство товара и проявление потребителями на рынке своей покупательской активности являются нестационарными пуассоновскими процессами, то функция 
имеет смысл зависимости от времени интенсивности изготовления товара, а функция 
– временной зависимости интенсивности покупательской активности потребителей. В этом случае математическое ожидание количества проданного товара (18) принимает вид
(19)
На рис. 3 показана динамика ежемесячных объемов продаж и объемов производства автомобилей «Лада Веста» в России в период с октября 2015 г. (t = 0, старт производства автомобилей этой марки) по май 2023 г.
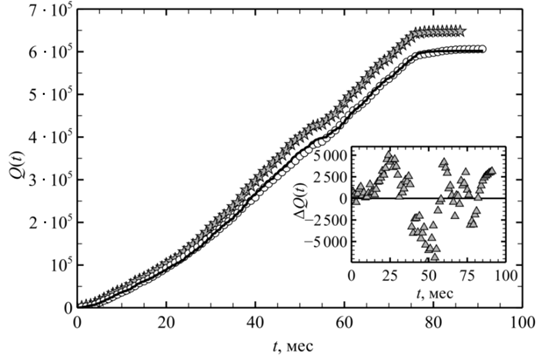
Рис. 3. Количество автомобилей «Лада Веста», произведенных (звездочки) за время t и купленных (кружки)
за время t в России в период с октября 2015 г. по май 2023 г.
Fig. 3. The number of Lada Vesta cars produced (asterisks) during t and purchased (mugs) during t
in Russia in the period from October 2015 to May 2023.
Для построения использовались данные, находящиеся в открытом доступе на интернет-портале Auto.VERcity в разделе «Статистика» [6]. Как видно из рис. 3, в любой момент времени количество проданных и количество произведенных автомобилей «Лада Веста» примерно одинаковы. С одной стороны, это говорит о том, что рынок автомобилей «Лада Веста» в России находится в состоянии, близком к равновесному, а с другой стороны, о том, что отдельные экземпляры этих автомобилей характеризуются низкой доступностью для потребителей на фоне больших объемов производства. Следовательно, на рынке автомобилей «Лада Веста» реализуется ситуация p(x, y) = p0 ≪ 1, и для описания динамики объемов продаж этих автомобилей можно пользоваться формулами (18), (19).
Поскольку временная зависимость интенсивности производства автомобилей «Лада Веста» в России известна (см. рис. 3), в качестве функции βg(t), входящей в (19), будем использовать эмпирическую дискретную функцию
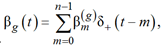(20)
где 
– данные интернет-портала Auto.VERcity об объеме производства автомобилей «Лада Веста» в России в месяце с номером m; m = 0 соответствует октябрю 2015 г.; n = 87 – количество месяцев, для которых имеется информация об объеме производства; 
– асимметричная дельта-функция Дирака, определяемая равенством
.
Данные о динамике покупательской активности потребителей на российском рынке автомобилей «Лада Веста» отсутствуют. По этой причине предположим, что эта активность является стационарным пуассоновским процессом с постоянной интенсивностью: βc(t) = βc – константа. Кроме того, как и при выводе формул (15), (16), будем считать, что периоды ликвидности автомобилей «Лада Веста» имеют показательный закон распределения. Используя эти приближения, подставляя (20)
в (19), находим:
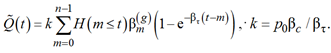(21)
Регрессионная модель (21) содержит всего
2 подгоночных параметра: k и βτ, однако из-за сложной нелинейной зависимости 
от βτ для определения этих параметров мы использовали не метод наименьших квадратов, а метод наибольшего косинуса, который позволяет найти βτ независимо от k [7]. Применение метода наибольшего косинуса для аппроксимации функцией (21) эмпирических данных об объемах продаж автомобилей «Лада Веста» в России приводит к следующим значениям регрессионных параметров k и βτ:
k ≈ 0,9286; 
. (22)
Сплошной линией на рис. 3 показана теоретическая зависимость от времени количества проданных в России автомобилей «Лада Веста», рассчитанная по формуле (21) с набором параметров (22). Очевидно, что теоретическая и эмпирическая зависимости хорошо согласуются друг с другом. Это дополнительно подтверждается вставкой на рис. 3, где изображена динамика разности ∆Q(t) между реальным количеством проданных автомобилей и значением этого количества, рассчитанным с помощью (21), (22). Действительно, эта вставка показывает, что, во-первых, разность ∆Q(t) в любой момент времени намного меньше, чем объем продаж 
: в среднем 
, а, во-вторых, отдельные значения ∆Q(t) достаточно хаотично и симметрично разбросаны вокруг нулевого уровня ∆Q(t) = 0.
Значение параметра βτ, приведенное в (22), означает, что в среднем покупатели автомобиля «Лада Веста» считают его период ликвидности примерно равным 11 дням:
Это довольно маленькое значение среднего периода ликвидности указывает на то, что покупатели хорошо осведомлены о высокой интенсивности и больших объемах производства автомобилей «Лада Веста» и поэтому при покупке рассчитывают получить автомобиль, который совсем недавно сошел с конвейера.
С помощью значения второго регрессионного параметра k можно оценить вероятность p0, которая определяет доступность автомобилей «Лада Веста» для потребителей на российском рынке. Поскольку интенсивность βc покупательской активности потребителей в любой момент времени больше или равна интенсивности βs продаж товара, то p0 удовлетворяет следующему неравенству: 
. Среднюю интенсивность продаж автомобилей «Лада Веста» легко найти
с помощью реальных данных по количеству автомобилей этой марки, ежемесячно продаваемых на российском рынке: 
. Отсюда, используя значения (22) параметров k и βτ, находим:
p0 ≤ 0,0004. Таким образом, вероятность p0 действительно очень мала, что доказывает справедливость предположения о применимости к российскому рынку автомобилей «Лада Веста» вероятностной модели (18), (19).
Ранее уже говорилось, что вероятность p0 представляет собой произведение двух вероятностей: p0 = p1p2. Применительно к рассматриваемому рынку автомобилей p1 – это усредненное за период с октября 2015 г. по май 2023 г. отношение текущего количества непроданных машин к текущему количеству произведенных автомобилей: p1 ≈ 0,13, а p2 имеет смысл усредненного за тот же период времени отношения текущего количества непроданных машин, находящихся на торговых площадках, доступных для потребителя, к текущему общему количеству непроданных машин. Учитывая значения вероятностей p0 и p1, находим: 
. В соответствии с определением вероятности p2 произведение этой вероятности на текущее количество непроданных автомобилей равно текущему количеству машин, доступных для покупки потребителю. Реальная динамика продаж автомобилей «Лада Веста» в России такова, что это количество доступных для покупки машин менялось от месяца к месяцу. В частности, вычисления, основанные на значении вероятности p2, показывают, что на рассматриваемом промежутке времени в первые полгода это количество было меньше 15 автомобилей, а в последние полгода находилось в диапазоне от 120 до 150 автомобилей. В среднем в период с октября 2015 г. по май 2023 г. количество автомобилей «Лада Веста», доступных на российском рынке для покупки потребителю, не превышало 92.
В отличие от кривых насыщения, изображенных на рис. 1, реальная динамика объемов продаж автомобилей «Лада Веста», показанная на рис. 3, имеет резкий выход на плато. Можно точно указать момент времени, начиная с которого интенсивность объемов продаж стала уменьшаться, стремясь к нулю: март 2022 г. Этот факт имеет очень простое объяснение. В феврале 2022 г. производители автомобилей «Лада Веста» на одном из своих заводов приступили к серийному производству существенно обновленной версии этой модели автомобилей. При этом старт продаж рестайлинговой версии «Лада Веста» был запланирован на весну-лето 2023 г. В ожидании этой новой версии потребители, естественно, снизили покупательскую активность, что и привело к резкому выходу на плато динамики продаж старой версии автомобилей «Лада Веста».
Заключение
Суммируя полученные результаты, приходим к заключению: простейшая вероятностная модель (2)–(4), а также ее обобщение (12), (13) правдоподобно учитывают влияние конечного периода ликвидности товара на динамику его продаж. Частные случаи (5)–(7) и (14)–(19) этих моделей содержат много параметров, манипулируя которыми продавцы могли бы управлять количеством продаваемого товара, а также длительностью его жизненного цикла. Некоторые из частных случаев, рассмотренных в настоящей работе, предполагают, что законы распределения вероятности моментов изготовления товара, моментов покупательской активности потребителей, периодов ликвидности, а также количества произведенного товара и количества потребителей имеют вполне определенный вид. Например, для использования формул (6), (7) нужно, чтобы моменты t1, t2, …, tN покупательской активности потребителей и периоды τ1, τ2, …, τN ликвидности товара подчинялись гамма-распределению (5). В условиях конкретного рынка это может оказаться не совсем корректным. Если это так, то необходимо в ходе статистического исследования определить свойственные данному рынку плотности распределения вероятностей 
, 
а также производящие функции вероятностей 
, после чего подставить их в формулы (2)–(4) или в (12), (13).
В результате получится присущая рынку зависимость математического ожидания реального объема продаж от параметров функций, 
. Если продавцы владеют механизмами изменения этих параметров, они получат возможность увеличивать количество товара, продаваемого за определенное время, а также уменьшать длительность его полной реализации.
В конечном итоге это будет способствовать увеличению прибыли продавцов, получаемой от продажи товара.
1. Пионткевич Н. С., Шатковская Е. Г., Долгих Ю. А. и др. Финансовый анализ: учеб. пособие. Екатеринбург: Изд-во Урал. ун-та, 2022. 190 с.
2. Тюленева Н. А. Современная методика анализа ликвидности бухгалтерского баланса // Проблемы учета и финансов. 2013. № 4 (12). С. 61-65.
3. Barardehi Y. H., Bernhardt D., Davies R. J. Trade-Time Measures of Liquidity // The Review of Financial Studies. 2019. V. 32, no. 1. P. 126-179.
4. Papoulis A., Pillai U. Probability, random variables and stochastic processes. N. Y.: McGraw-Hill, 2002. 852 p.
5. Olver F. W. J., Lozier D. W., Boisvert R. F., Clark C. W. NIST Handbook of Mathematical Functions. Cambridge; N. Y.; Melbourne: Cambridge University Press, 2010. 951 p.
6. Auto.VERcity. URL: https://auto.vercity.ru (дата обращения: 01.03.2023).
7. Михеев А. В., Казаков Б. Н. Новый метод точечной оценки параметров парной регрессии // Компьютерные исследования и моделирование. 2014. Т. 6, № 1. С. 57-77.
