Россия
Россия
Россия
сотрудник
Россия
Химический реактор является основным и наиболее сложным объектом в управлении технологическим процессом полимеризации. При проектировании химических реакторов необходимо подбирать конструктивные и режимные параметры, которые смогут обеспечить единственное или наиболее устойчивое состояние при заданных характеристиках процесса. Для исследования устойчивости процесса полимеризации этилена в автоклавном реакторе с мешалкой требуются построение математической модели на основе анализа физико-химических закономерностей процесса и поиск необходимых условий стационарного состояния для реактора. Предложено решение на основе детерминированной математической модели полимеризации этилена. Приведены описание процесса образования молекулы полимера, включающего в себя стадии инициирования, роста и обрыва цепи; механизм химической кинетики полимеризации этилена; система допущений для упрощения построения математической модели. Математическая модель реактора полимеризации этилена в автоклавном реакторе с мешалкой представляет собой систему дифференциальных уравнений. При расчете статического режима реактора математическое описание содержит систему нелинейных алгебраических уравнений, решение которых реализуется с помощью численных методов. Отмечено, что химические реакторы могут иметь не одно, а несколько стационарных состояний при одних и тех же значениях переменных и параметров. Зная координаты стационарных состояний химического процесса, можно выбрать то из них, которое более предпочтительно с точки зрения производительности или качества производимой продукции. В результате моделирования подтверждено наличие единственного решения при найденных условиях, обеспечивающих устойчивое стационарное состояние химического реактора полимеризации этилена.
автоклавный реактор, математическая модель реактора, полимеризация этилена, устойчивость химического реактора, мономер, инициатор, стационарное состояние
Описание процесса полимеризации
Процесс полимеризации этилена осуществляется в автоклавном реакторе с перемешивающим устройством. Реактор снабжен рубашкой, в которую подается охлаждающий воздух. Этилен поступает в реактор одновременно с инициатором для инициирования реакции полимеризации этилена.
Температура в реакторе регулируется изменением расхода этилена и инициатора в зависимости от применяемого инициатора и выпускаемой марки полиэтилена.
В реакторе осуществляется процесс образования высокомолекулярного вещества (полимера) путем взаимного соединения большого числа молекул исходного низкомолекулярного вещества (мономера), включающего следующие стадии [1]:
1) инициирование – образование первичного свободного радикала:
;
2) рост цепи – последовательное присоединение к радикалу молекул мономера с сохранением свободной валентности на конце растущей молекулы:
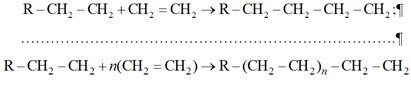
3) обрыв цепи – прекращение роста молекулы (взаимодействие двух растущих радикалов с образованием одной или двух неактивных молекул полиэтилена рекомбинацией или диспропорционированием):
– рекомбинацией:
– диспропорционированием:
Если через M обозначить мономер (этилен), инициатор через I, радикал (активную молекулу) через X, а полимер через P, то схематически реакцию полимеризации можно изобразить:
– как инициирование:
;
– рост цепи:
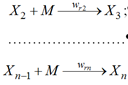
– обрыв цепи:
где индекс, стоящий при X, определяет степень полимеризации (т. е. длину цепи), а wi, wri , wo – скорости реакций инициирования, роста и обрыва цепи соответственно.
Система допущений
При образовании полимеров, мольные массы которых велики, с хорошим приближением можно принять, что скорости реакций роста радикала, имеющего i-ю степень полимеризации wri, не зависят от степени полимеризации, т. е. wri = wr при любом i [1]. Это позволяет ввести суммарную концентрацию всех радикалов 
и упростить схему реакций полимеризации следующим образом:
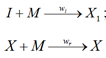
Через X обозначены все радикалы, независимо от числа молекул мономера, входящих в их состав, т. е. от степени полимеризации.
Так как число молекул мономера, участвующих при инициировании в реакции с первичным радикалом, очень мало по сравнению с числом молекул мономера, участвующих в росте цепи (инициатор вводится в количестве до 1 % от массы мономера), примем допущение о том, что мономер расходуется только на полимеризацию [1].
В предположении об идеальности перемешивания и постоянном давлении автоклавный реактор полимеризации можно представить как аппарат идеального смешения. Схема потоков в реакторе полимеризации показана на рис. 1.
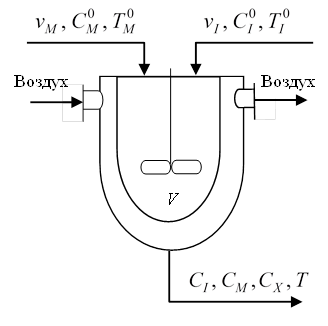
Рис. 1. Схема потоков в реакторе: vM, vI – объемные расходы мономера и инициатора соответственно, м3/с;
– массовые концентрации мономера и инициатора на входе реактора, кг/м3;
CI, CM, CX – массовые концентрации инициатора, мономера и активных молекул на выходе реактора;
– температура входных и выходного потоков реактора, °С; V – реакционный объем, м3
Fig. 1. Flow diagram in the reactor: vM, vI – volume flow rates of the monomer and initiator, respectively, m3/s;
– mass concentrations of the monomer and initiator at the reactor inlet, kg/m3;
CI, CM, CX – mass concentrations of the initiator, monomer and active molecules at the reactor outlet;
– temperature of the inlet and outlet flows of the reactor, °C; V – reaction volume, m3
Нагрев перед пуском и охлаждение реактора в процессе полимеризации этилена осуществляется воздухом через поверхность рубашки. Вследствие небольшого объема реактора примем допущение, что температура охлаждающего воздуха в рубашке одинакова во всем объеме.
Теплофизические свойства потоков (тепловой эффект реакции, удельные теплоемкости, плотности и т. п.) будем считать постоянными, не зависящими от состава потоков.
Математическое описание реактора
По закону действующих масс скорость химической реакции инициирования wi можно представить как
,
где ki 
– константа скорости инициирования; Ei
– энергия активации реакции инициирования; R – универсальная газовая постоянная; T – температура.
Скорость химической реакции роста цепи wr выражается уравнением
, (1)
где kr – константа скорости роста цепи; Er – энергия активации реакции роста цепи.
Скорость химической реакции для обрыва цепи wo запишем как
,
где ko – константа скорости обрыва цепи; Eo
– энергия активации реакции обрыва цепи.
Так как реактор проточный и на его входы подаются мономер и инициатор, то уравнения материального и теплового баланса по этим веществам можно представить в виде модели идеального смешения для непрерывного реактора.
Так, уравнение материального баланса по инициатору можно представить в виде
,
где t – время.
Уравнение материального баланса по мономеру с учетом того, что мономер расходуется только на реакцию полимеризации, можно представить в виде уравнения
.
Уравнение материального баланса по радикалу выглядит следующим образом:
, (2)
где 
– концентрация радикалов (активных молекул) на входе в реактор.
Примем допущение, что нет накопления радикалов в объеме реактора (
), т. е. все образующиеся радикалы расходуются на реакцию полимеризации (условие квазистационарности [2–4]), и поскольку нет радикалов во входных и выходном потоке, уравнение (2) примет вид
или
.
Отсюда можно выразить концентрацию радикалов
.
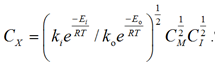Тогда уравнение скорости химической реакции роста цепи (1) можно представить как
. (3)
В уравнении (3) выражение 
есть константа скорости полимеризации k, а E – суммарная энергия активации процесса полимеризации, которая находится как
.
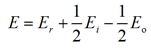С учетом выражения скорости реакции (3) материальный баланс по мономеру примет вид
.
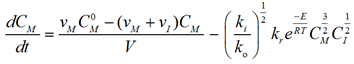Уравнение теплового баланса будет иметь вид
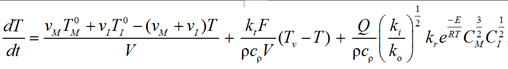
где kt – коэффициент теплопередачи, Дж/(м2∙с∙°C); F – поверхность теплообмена, м2; ρ – плотность потока, кг/м3; cρ – удельная теплоемкость потока, Дж/(кг∙°C); Tv – температура воздуха в рубашке реактора; Q – тепловой эффект реакции полимеризации, Дж/моль.
В итоге математическая модель реактора представляет систему из трех обыкновенных дифференциальных уравнений
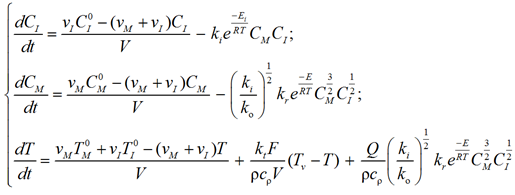(4)
с начальными условиями
(5)
и одного конечного уравнения
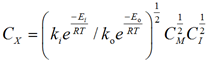. (6)
Математическая модель реактора полимеризации (4)–(6) содержит начальные условия (5), которые неизвестны и могут быть определены из решения уравнений модели статики. При расчете статического режима производные дифференциальных уравнений в модели приравниваются к нулю и математическое описание переходит в систему нелинейных алгебраических уравнений следующего вида:
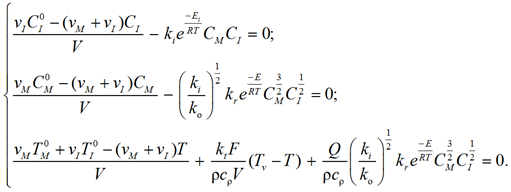(7)
Получение решения уравнений модели не вызывает каких-либо трудностей и может быть реализовано с помощью известных численных методов. Так, для решения системы нелинейных алгебраических уравнений (7) использовался метод Ньютона – Рафсона, а для решения систем дифференциальных уравнений (4) – метод Рунге – Кутта 4-го порядка.
Устойчивость химического реактора полимеризации
Химические реакторы могут иметь не одно, а несколько стационарных состояний при одних и тех же значениях переменных и параметров. Под стационарным состоянием понимается как установившийся режим динамической системы (статика), так и режим термодинамического равновесия, когда все макропроцессы прекращены и система находится в режиме равновесия [5–7]. В обоих случаях выходные переменные – концентрации компонентов и температуры потоков – не меняются во времени.
Основным фактором, влияющим на устойчивость реактора полимеризации этилена в автоклавном реакторе с мешалкой, является температура. Так, в химическом реакторе для экзотермического процесса необходимо обеспечить нужное отведение тепла, т. е. выделяемое в процессе реакции тепло должно быть равно отводимому теплу.
На рис. 2 приведены графики выделяемого Qв и отводимого Qo тепла (экспоненциальная зависимость и прямые параллельные линии соответственно).
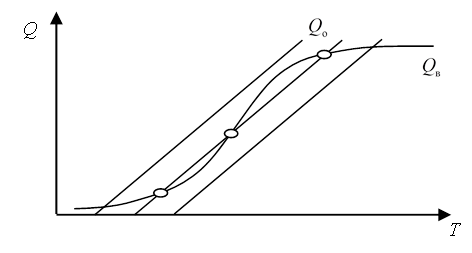
Рис. 2. Количество выделяемого и отводимого тепла при проведении экзотермической реакции
Fig. 2. The amount of heat released and removed during an exothermic reaction
На рисунке видно, что отводимое тепло Qo связано с температурой линейной зависимостью. Действительно, в выражении для отводимого тепла 
конструктивные параметры kt, F, V и входная переменная Tv постоянны. Выделяемое же тепло Qв, которое находится как 
, зависит от температуры Т нелинейно.
В общем случае возможны:
– отсутствие решения (линии Qв и Qo не пересекаются);
– единственное решение (одна точка пересечения);
– два или три решения (две или три точки пересечения).
Расчетная множественность стационарных состояний лишь означает, что реальный процесс «выберет» одно из них, наиболее устойчивое.
При проектировании реактора подбирают такие конструктивные и режимные параметры, которые обеспечивают единственное или наиболее устойчивое состояние при заданных характеристиках процесса. Найдем условия, обеспечивающие устойчивое стационарное состояние для реактора полимеризации этилена.
Определим вначале, является ли стационарное состояние непрерывной произвольной функции f(x), удовлетворяющей условию f(x) = 0, единственным. При наличии, по крайней мере, двух решений f(x1) = 0 и f(x2) = 0 в области [x1, x2] должна быть промежуточная точка x, при которой 
. Если удастся доказать, что в исследуемой области 
это будет означать отсутствие или единственность решения [6].
Для объекта, описываемого системой уравнений (7), или в общем виде
применить это условие затруднительно, поэтому применяются приемы, позволяющие перейти
к функции одной переменной.
Из системы уравнений (7) видно, что с реакцией полимеризации этилена связаны концентрации инициатора, мономера и температуры. Выразим из второго уравнения системы (7) концентрацию инициатора CI, получим
.
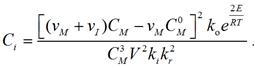Подставим полученное выражение во второе уравнение системы (7) вместо CI:
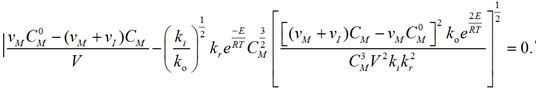
Теперь скорость реакции полимеризации этилена зависит только от концентрации мономера и температуры и выражается уравнением
.
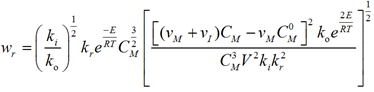Представим второе и третье уравнения системы (7) в следующем виде:
(8)
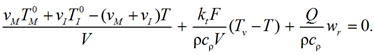(9)
Выразим wr из уравнения (8) и подставим в уравнение (9):
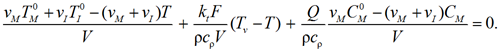
Выразим из него концентрацию мономера CM:
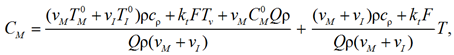
тогда
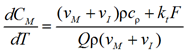
Таким образом, 
.
Запишем уравнение теплового баланса (9) в виде
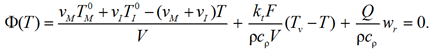
Продифференцируем Φ по Т:
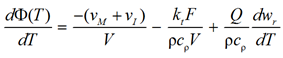. (10)
Продифференцируем wr по Т:
и подставим полученное выражение в (10). Если
то 
, и система имеет несколько стационарных состояний. Если же
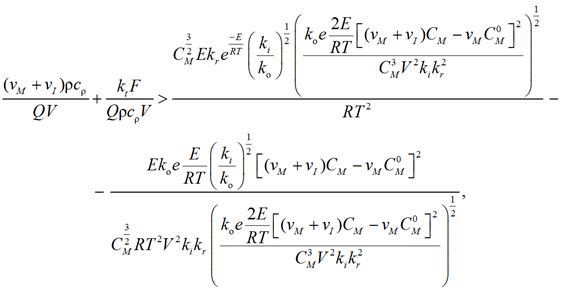(11)
то возможно только одно стационарное состояние.
Найденное условие позволяет обеспечить устойчивое стационарное состояние реактора, выбирая соответствующим образом конструктивные параметры kt, F, V и входные переменные 
.
В таблице приведены числовые данные при моделировании процесса полимеризации этилена в автоклавном реакторе с мешалкой (кинетические константы взяты из работы [5]).
Значения входных переменных и констант реактора и модели
Values of input variables and constants of the reactor and model
|
Показатель |
Значение |
Показатель |
Значение |
|
Объемный расход мономера, м3/c |
0,0037 |
Константа инициирования, м3/кг∙с |
2 ∙ 1016 |
|
Концентрация мономера, кг/м3 |
445 |
Константа роста цепи, м3/кг∙с |
1 000 |
|
Объемный расход инициатора, м3/c |
5,12 ∙ 10–4 |
Константа обрыва цепи, м3/кг∙с |
1 |
|
Концентрация инициатора, кг/м3 |
1,2 |
Энергия активации инициирования, Дж/моль |
45 000 |
|
Температура мономера, К |
310 |
Энергия активации роста цепи, Дж/моль |
180 000 |
|
Температура инициатора, К |
293 |
Энергия активации обрыва цепи, Дж/моль |
18 000 |
|
Объем реактора, м3 |
0,25 |
Универсальная постоянная, Дж/моль∙К |
8,31 |
|
Коэффициент теплопередачи, Дж/м2 ∙ с∙°C |
5 |
Тепловой эффект полимеризации, Дж/моль |
96 000 |
|
Поверхность теплообмена, м2 |
15 |
Плотность потока, кг/м3 |
400 |
|
Температура воздуха, К |
293 |
Удельная теплоемкость потока, Дж/кг∙°C |
2 000 |
Согласно расчетам исследуемый реактор имеет единственное стационарное состояние в соответствии с условием (11). Моделирование подтвердило единственность решения при различных начальных приближениях выходных переменных: CI = 6,77 · 10–4 кг/м3, CM = 381 кг/м3, CХ = 2,41 · 10–8 кг/м3, Т = 509 К.
Заключение
Для химических реакторов процесса полимеризации этилена возможно несколько стационарных состояний при одних и тех же значениях переменных и параметров. Зная координаты стационарных состояний химического процесса, можно выбрать то из них, которое обеспечит устойчивое стационарное состояние реактора с точки зрения производительности или качества производимой продукции.
1. Технология полимерных материалов / под ред. В. К. Крыжановского. СПб.: ЦОП «Профессия», 2011. 536 с.
2. Климов И. Г. Радикальная полимеризация этилена в трубчатых и автоклавных реакторах // Изв. Томск. политехн. ун-та. 2010. Т. 317, № 3. С. 174-177.
3. Софиев А. Э., Янкина И. А. Применение математического моделирования для построения алгоритмов пуска и противоаварийной защиты химических реакторов // Вестн. Тамбов. гос. техн. ун-та. 2011. Т. 17, № 1. С. 17-23.
4. Вафина Л. Р. Построение модели реактора поли-меризации этилена для получения полиэтилена высокого давления // Science Time. 2016. № 2 (26). С. 101-104.
5. Вольтер Б. В., Сальников И. Е. Устойчивость режимов работы химических реакторов. М.: Химия, 1981. 200 с.
6. Жоров Ю. М. Моделирование физико-химических процессов нефтепереработки и нефтехимии. М.: Химия, 1978. 376 с.
7. Перлмуттер Д. Устойчивость химических реакторов / под ред. Н. С. Гурфейна. Л.: Химия, 1976. 256 с.
