Объектом исследования является новый методологический подход к адаптивной нейросетевой фильтрации как к математическому инструменту повышения точности и оперативности оценки некоторых свойств сложных технических систем. Данный подход представляет собой один из вариантов практического приложения методов адаптивной (гибридной) фильтрации. Проведен анализ особенностей этого подхода, определяющих рациональность его применения для оперативной оценки защищенности критически важных ресурсов. Рассмотрены теоретические аспекты применения гибридного адаптивного подхода к оперативной оценке защищенности критически важных ресурсов, сочетающего традиционные методы фильтрации Калмана с возможностями искусственных нейронных сетей с обучением. Проведен анализ особенностей такого подхода, по- зволяющего обучаться и подстраивать весовые коэффициенты фильтрации под статистические характеристики показателей защищенности критически важных ресурсов, измеряемых и наблюдаемых как линейно, так и нелинейно. Предложена последовательность вычислений и аналитические выражения для расчетов оценочных значений вспомогательных индикаторов состояния показателей защищенности на основе адаптивного гибридного фильтра, содержащего в своем составе обучаемую искусственную нейронную сеть. Подход предполагает практическую возможность оперативной оценки защищенности критически важных ресурсов с использованием адаптивной гибридной фильтрации случайных процессов, характеризующих динамику изменения переменных состояния (показателей) защищенности таких ресурсов на определенном временном интервале. Он учитывает неопределенность исходных данных, неполноту и нечеткость априорных сведений о статистике показателей защищенности и шумов наблюдения. При этом предложенный подход позволяет получать оценки, адекватные задачам оперативного контроля защищенности и, в конечном итоге, обеспечивает повышение достоверности контроля информационной безопасности современных критически важных ресурсов.
критически важный ресурс, защищенность, оперативная оценка, адаптивный гибридный фильтр, нейронная сеть, фильтрация, показатель защищенности
Введение
Принятие решения о текущих количестве и уровне нарушений политики безопасности критически важных ресурсов (КВР), своевременное и оптимальное управление рисками их информационной безопасности традиционно организуются и осуществляются на основе процедур наблюдения (сбора и предобработки больших массивов гетерогенных данных о событиях кибербезопасности) и достоверной оперативной оценки защищенности объектов такого класса [1, 2]. При этом необходимо учитывать различные типы априорных гетерогенных данных о событиях кибербезопасности – данные, обусловленные различными форматами файлов, протоколов доступа, языков запросов и т. д. (техническая гетерогенность, синтаксическая гетерогенность); данные, обусловленные неоднородностью моделей представления, когда схемы кодирования данных могут различаться,
а также случаи, когда поступают семантически похожие, взаимосвязанные, но разные по сути наборы данных, необходимых для анализа (семантическая гетерогенность). Источниками таких априорных данных могут выступать данные систем обнаружения и предотвращения вторжений, сетевых экранов, журналов приложений и штатных средств контроля безопасности, представляемые в виде лог-файлов, датасетов на основе собираемой статистики, видеоизображений. Практика показывает, что в условиях возможного воздействия на КВР различного рода атак и иных негативных кибервоздействий особое значение приобретает задача оперативной оценки информационной безопасности, т. е. задача определения наиболее вероятного состояния защищенности объектов такого класса в момент времени t. Такую оценку можно получить на основе априорных данных о КВР, условиях их использования и доступа к ним, а также на основе наблюдений и/или измерений всех или части переменных состояния (параметров, показателей) защищенности КВР на интервале (t0, t), производимых с ошибками либо в условиях различного рода неопределенности [3–5].
Как известно, задача определения наиболее вероятных значений переменных состояния (параметров, показателей) называется фильтрацией случайных процессов, включая, например, такие, как процесс смены состояний защищенности КВР. При этом под состоянием защищенности КВР на интервале (t0, t) или в момент времени t будем понимать численное оценочное значение переменных состояния (параметров, показателей) защищенности КВР на этом интервале. Причем для традиционных задач фильтрации таких случайных процессов предполагается известным необходимый объем априорных сведений о статистике показателей защищенности (ПЗ) КВР, шумов процесса, шумов наблюдения и об их взаимодействии [6]. В реальной ситуации такая априорная информация недоступна и обычными являются случаи, когда в рамках реализации задач фильтрации имеет место достаточно большая априорная неопределенность различного рода. Например, неопределенность типа неполноты (нечеткости, противоречивости), связанная с трудностью выбора модели нарушителя, учета особенностей обеспечения информационной безопасности или выбора модели КВР и их ПЗ.
Существующие трудности создания современных подходов к оперативной оценке защищенности КВР, сложности решения задачи учета неопределенности типа неполноты (нечеткости, противоречивости) в рамках многокритериального анализа защищенности – сложноразрешимы. Это обусловлено, в том числе, отсутствием универсальных методов, учитывающих особенности процедур оперативного анализа, неполноту и неоднородность исходной информации о параметрах защищенности КВР в целом. Поэтому разработка новых методов достоверной и оперативной оценки защищенности КВР в условиях неопределенности (неполноты, нечеткости и противоречивости) исходных данных является актуальной, важной задачей.
Анализ релевантных работ
Созданию методов достоверной и оперативной оценки защищенности всех видов ресурсов, предоставляемых пользователям сложными управляемыми информационными и организационно-техническими системами, посвящено большое количество современных исследований [3, 5, 7–15]. Результаты этих исследований детально иллюстрируют всевозможные подходы к оценке защищенности, которые обладают несомненными достоинствами, но не всегда реализуемы на практике и зачастую не адекватны задачам, решаемым в рамках оперативного анализа в условиях неопределенности.
Трудности применения известных методов связаны, в частности, с необходимостью учета динамики переходных процессов, обуславливающих смену состояний параметров защищенности реальных КВР. Помимо этого в рамках оперативной оценки большое значение имеет необходимость учета многокритериального характера современных требований, предъявляемых к защищенности КВР, который в существующих методах не рассматривался.
В работах [7, 8] оперативную оценку защищенности предложено реализовать на основе контроля и управления рисками информационной безопасности. Но такие методы основаны на больших вычислительных затратах, необходимых для их практической реализации.
Результаты работ [9, 10] позволяют говорить о том, что предусмотренный в этих методах сбор статистики о состоянии ПЗ сложных технических систем обуславливает большие временные затраты на сбор этих больших объемов гетерогенных данных, что негативно влияет на оперативность оценки защищенности.
Исследования, нашедшие отражение в работах [11, 12], посвящены методам повышения точности оперативной оценки защищенности. Но в этих работах в качестве критерия точности используется дисперсия ошибки оценивания, которая равна априорной дисперсии самого исследуемого процесса обеспечения защищенности КВР. Это неприемлемо для современных высокоточных систем оперативной оценки, ориентированных на повышенную достоверность анализа ПЗ.
Повышение достоверности оперативной оценки защищенности может быть практически реализовано, например, на основе искусственных нейронных сетей (ИНС) [13–15]. Искусственные нейронные сети позволяют учесть неполноту и противоречивость исходных данных, но рациональное их использование ожидается при интеграции с иными, адаптивными способами анализа, позволяющими устранить априорную неопределенность измеряемых (наблюдаемых) ПЗ КВР.
Одним из основных подходов, применяемых для преодоления априорной неопределенности при решении подобных задач, являются методы и алгоритмы адаптивной фильтрации [16–18]. Сегодня теория фильтрации приобрела «новое звучание» в связи с возникшей необходимостью синтеза адаптивных систем, которые можно эксплуатировать в условиях априорной неопределенности исходной информации о свойствах объекта и внешней среды.
Не секрет, что в большинстве практических задач контроля и управления, например задач оперативной оценки защищенности КВР, используется априорная информация. Однако, если априорная информация недоступна создателям оптимальных фильтров, ее можно (в определенной степени) восполнить из анализа наблюдаемых, зашумленных параметров объекта оценки, т. е. из наблюдения ПЗ КВР.
Если недостающие сведения успешно восполнены для решаемых задач, фильтр приобретает оптимальные (либо близкие к оптимальным) свойства. Такие фильтры называют гибридными, адаптивными, а сам процесс оценивания – адаптивной фильтрацией [16–18].
Таким образом, анализ релевантных работ позволяет говорить об объективной необходимости развития существующих методов анализа, алгоритмов оперативной оценки защищенности КВР на случай учета большого числа статистических характеристик ПЗ КВР, измеряемых и наблюдаемых как линейно, так и нелинейно.
Методологической и математической базой такого анализа может выступать гибридная адаптивная фильтрация – подход к оперативной оценке защищенности КВР, сочетающий традиционные методы фильтрации Калмана с возможностями ИНС с обучением.
Теоретические аспекты построения процедур адаптивной нейросетевой фильтрации для задач контроля защищенности
Применение адаптивных фильтров для задач контроля защищенности КВР делает процесс оперативной оценки более гибким, однако реализация адаптивных фильтров становится более сложной, требует большего объема вычислений и памяти вычислительных устройств. На наш взгляд, успешное создание адаптивных фильтров для задач оперативной оценки защищенности КВР возможно на пути развития рекуррентного синтеза, когда «настройка» параметров фильтра осуществляется вновь по мере поступления новых массивов гетерогенных данных наблюдения о текущих значениях ПЗ КВР на интервале (t0, t).
Такой подход позволит сохранить разумный компромисс между необходимым быстродействием вычислительных устройств с требуемым объемом памяти для задач оперативной оценки с тем, чтобы обеспечить своевременную обработку больших объемов гетерогенных данных наблюдения о значениях ПЗ КВР.
В работе [19] предложена модель процесса поддержки принятия решений по управлению событиями и инцидентами безопасности, а также рассмотрены алгоритмы фильтрации, конкретизированные на случай оценивания состояний управляемых марковских цепей. Эти алгоритмы базируются на методах калмановской фильтрации, причем оптимальную в смысле минимума среднеквадратичной ошибки (МСКО) оценку по всем поступившим на данный момент наблюдениям о значениях ПЗ КВР можно вычислить соотношениями фильтра Калмана [20]. Однако данные вычисления корректны и осуществимы лишь тогда, когда элементы матрицы шумов возбуждения Vξ(k + 1) процесса смены состояний ПЗ КВР Y(k + 1) и элементы матрицы шумов наблюдения Vη(k + 1) за этим процессом предполагаются известными. Причем в рамках калмановской фильтрации для математических моделей процессов смены состояний ПЗ КВР данные соотношения могут быть записаны в виде рекуррентных уравнений для вспомогательных индикаторов состояния [20]
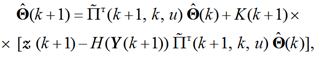(1)
где 
– векторы вспомогательных индикаторов состояния на следующем (k + 1) и предыдущем (k) шаге процесса смены состояний; 
– транспонированная (надстрочный символ т указывает на транспонированную матрицу либо вектор) матрица, содержащая одношаговые переходные вероятности для описания процесса смены состояний ПЗ КВР в рамках цепи Маркова; 
– диагональная матрица наблюдаемых значений процесса смены состояний; 
– матрица наблюдений за процессом смены состояний;
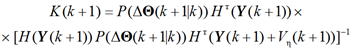(2)
– коэффициент усиления фильтра Калмана, учитывающий значения элементов транспонированной матрицы 
, диагональной матрицы наблюдаемых значений процесса смены состояний 
и значения элементов матрицы шумов наблюдения 
за процессом смены состояний элементов вектора Y(k + 1) ПЗ КВР;
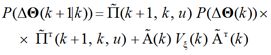(3)
– матрица априорных дисперсий ошибок оценивания вспомогательных индикаторов состояния 
, где 
– единичная диагональная матрица состояния;
(4)
– матрица апостериорных дисперсий ошибок оценивания, где E – единичная диагональная матрица наблюдения, причем должны быть выполнены начальные условия:
Вспомогательный индикатор состояний (1) представляет собой вектор дискретных по состоянию последовательностей возбуждения процесса смены состояний элементов вектора Y(k + 1) ПЗ КВР, принимающий значение 0 или 1 [20].
Если элементы матриц Vξ(k) и Vη(k) частично или полностью неизвестны, возникает необходимость синтезировать адаптивные алгоритмы фильтрации. Существует множество различных адаптивных алгоритмов фильтрации, однако в настоящее время широкое распространение получают методы, основанные на теории ИНС [14, 15, 17, 18, 21, 22].
Искусственные нейронные сети давно нашли применение в теории управления, прогнозировании и идентификации, но впервые исследования приложений ИНС в теории фильтрации предложены в работе [17], где доказано, что фильтр состояния, основанный на рекуррентных нейронных сетях, сходится к оптимальному фильтру Калмана
с минимальной дисперсией.
Алгоритм калмановской фильтрации (1)–(4) для математических моделей процессов смены состояний ПЗ КВР подходит для линейного характера изменений большинства этих показателей и позволяет получить оптимальные в смысле критерия МСКО оценочные значения вспомогательных индикаторов состояния 
в реальном времени. Это в конечном итоге позволяет перейти к вероятностно-временной оценке защищенности КВР синтезом вероятностных характеристик на основе полученных оценочных значений.
Несколько иначе обстоит дело с теми ПЗ КВР из состава вектора Y(k + 1), механизм изменения которых носит нелинейный характер. В этом случае имеется объективная необходимость в решении задачи синтеза алгоритмов нелинейной фильтрации, например, с применением расширенных фильтров Калмана (РФК). Расширенные калмановские фильтры довольно широко используются для оценивания нелинейных систем, но являются достаточно сложными для реализации, трудно настраиваемыми. Более того, получаемые с их помощью оценки можно признать относительно достоверными лишь для объектов анализа, которые в масштабе времени обновлений являются почти линейными. Исследования показывают, что многие из этих трудностей возникают по причине вынужденного использования в РФК линеаризованной модели процесса наблюдения [21, 22].
Решением данной проблемы, на наш взгляд, является использование адаптивных фильтров с применением ИНС. Данный подход в рамках рассматриваемых задач оперативного анализа защищенности КВР призван позволить алгоритмам оценки «подстраиваться» под статистические характеристики измеряемых и наблюдаемых ПЗ КВР и учитывать их нелинейность [21–23]. В этой связи особого внимания, по нашему мнению, заслуживает подход к построению адаптивных оптимальных фильтров с использованием так называемого гибридного метода. Он частично основан на базовых правилах фильтрации Калмана, однако использует и рекуррентные нейронные сети или ИНС прямого распространения [18].
Уникальные способности ИНС аппроксимировать нелинейные функции нескольких переменных различной сложности в сочетании с калмановским фильтром делают предлагаемый симбиоз адаптивным и эффективным. Более того, в работе [18] доказано, что, несмотря на отсутствие априорных данных о статистических характеристиках шумов возбуждения фильтруемого процесса и шумов наблюдений, предлагаемый гибридный метод позволяет получить так называемый оптимальный фильтр в смысле критерия МСКО.
Вариант структурной схемы типового адаптивного гибридного фильтра (АГФ) может быть сформирован для модели в виде управляемой цепи Маркова в интересах описания процесса смены состояний всех классов ПЗ КВР в форме разностных стохастических уравнений. При этом нейронные сети в его составе используются для того, чтобы смоделировать некоторые из функциональных соотношений, входящих в данный фильтр.
Вариант структурной схемы типового АГФ включает блок прогноза (экстраполятор), представляющий собой механизм реализации модели процесса смены состояний ПЗ КВР, и блок обновления, состоящий из сумматора, блока задержки, двух линий задержки, схемы адаптации в режиме реального времени и ключевого элемента АГФ – нейросетевого фильтра (НСФ), представляющего собой ИНС прямого распространения, или многослойный персептрон (МСП). Это, по сути, сетевая структура из простых вычислительных элементов (узлов, нейронов), сгруппированных в соединенные последовательно слои.
По аналогии с классическим калмановским фильтром АГФ рекурсивен, т. е. каждая обновленная оценка состояния 
вычисляется на основе предыдущей оценки состояния 
и новых измерений (наблюдений) Z(k + 1). Так же, как и в калмановском фильтре, он включает два последовательных этапа обработки наблюдений: прогнозирование (экстраполяция) и обновление (коррекция). При этом имеется отличительная особенность, которая заключается в том, что алгоритм фильтрации по Калману использует только последние наблюдения, а при данном подходе этап обновления может иметь общую нелинейную форму и использовать определенное количество mz «прошлых» наблюдений, в нашем случае – наблюдений за значениями ПЗ КВР.
Известно, что аналитическая формулировка и вычисления для нелинейного фильтра состояния являются достаточно трудоемкими и часто приводят к ошибкам даже для известных, хорошо апробированных моделей [21]. В этих условиях нейросетевой метод для новой модели, предложенной в интересах оперативной оценки защищенности КВР, способен дополнительно «обучить» АГФ соотношению (коэффициенту усиления нейросетевого фильтра) KНСФ(k + 1), эквивалентному по функциональности и по физической сущности коэффициенту усиления классического фильтра Калмана [18].
Методологические особенности адаптивной нейросетевой фильтрации для получения оценок вспомогательных индикаторов состояния значений показателей защищенности
С учетом особенностей решаемой задачи процедура нейросетевой (гибридной адаптивной) фильтрации для получения оценочных значений вспомогательных индикаторов состояний значений ПЗ КВР, т. е. элементов вектора-столбца 
, включает следующие шаги.
Шаг 1 – расчет априорных оценочных значений векторов-столбцов состояния процесса и наблюдения за процессом смены состояний ПЗ КВР на
(k + 1)-м шаге (стадия прогноза АГФ):
,
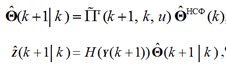где 
– экстраполированные оценки значений векторов-столбцов состояния процесса и наблюдения за процессом смены состояний ПЗ КВР на (k + 1)-м шаге соответственно; 
– нейросетевая оценка значений вектора-столбца состояний ПЗ КВР на предыдущем, k-м, шаге анализа.
Шаг 2 – расчет апостериорной оценки значений вектора-столбца индикаторов состояний ПЗ КВР на (k + 1)-м шаге оперативного анализа защищенности (стадия обновления АГФ):
(5)
где KНСФ – нелинейная передаточная вектор-функция, эквивалентная коэффициенту усиления фильтра Калмана; Z(k + 1) – вектор-столбец, содержащий текущее наблюдение за значениями ПЗ КВР на (k + 1)-м шаге оперативного анализа защищенности, а также набор их значений с предыдущих шагов; E(k + 1) – вектор-столбец, содержащий текущую невязку АГФ на (k + 1)-м шаге, а также набор значений невязки с предыдущих шагов.
Векторы Z(k + 1) и E(k + 1) содержат следующие элементы – данные наблюдений и невязок:
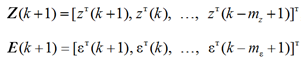
где mz – глубина линии задержки для вектора наблюдений; mε – глубина линии задержки для вектора невязки наблюдений, используемых соответственно в АГФ, а
– вектор-столбец невязок АГФ, вычисляемый в блоке обновления на (k + 1)-м шаге оперативного анализа защищенности КВР. При этом с целью упрощения
и условной формализации дальнейшего изложения введем R-мерный входной вектор-столбец НСФ, где
– входной вектор-столбец НСФ, представляющий собой, с точки зрения фильтрации, вектор-столбец оцениваемых (наблюдаемых, измеряемых) ПЗ КВР Y(k + 1) в виде
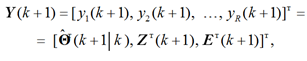
где M – размерность транспонированного вектора индикаторов состояния 
, транспонированного вектора наблюдения 
, а значит, и транспонированного вектора-столбца 
, содержащего текущую невязку АГФ на (k + 1)-м шаге, т. е. число состояний ПЗ КВР.
Поскольку векторное отображение нейронной сетью входа Y(k + 1) на выход 
, выполненное вектор-функцией KНСФ (выражение (5)), является статическим, можно утверждать, что нейронной сети прямого распространения типа МСП в интересах решения задач оперативной оценки защищенности КВР будет достаточно для аппроксимации этой функции. При этом исследования показывают, что для получения подобных состоятельных и субоптимальных (в смысле МСКО) оценок достаточно МСП, состоящего из трех слоев [21].
Пример такого МСП для реализации функций адаптивной гибридной нейросетевой фильтрации детально описан в работе [21]. В нашем случае для решения задач оперативной оценки защищенности КВР тоже достаточно трех слоев НСФ, причем первый слой – распределительный – будет включать R входных узлов, скрытый слой будет состоять из D нейронов с нелинейными функциями активации типа гиперболического тангенса, а выходной слой включает M нейронов с нелинейными функциями активации сигмоидального типа [21]. Как и для классического МСП, состоящего из трех слоев, промежуточный и выходной слои АГФ для оперативной оценки защищенности КВР имеют постоянное смещение, равное 0, поэтому в расчетах данное смещение можно не учитывать. Весовые матрицы промежуточного ΩI и выходного ΩII слоя определяются как
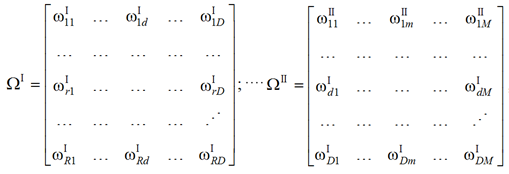
для r = 1, …, R, d = 1, …, D, m = 1, …, M.
Процедуру обучения МСП для оперативной оценки защищенности КВР можно разделить на две фазы.
В первой фазе НСФ для оперативной оценки защищенности КВР настраивается на истинных значениях вспомогательных индикаторов состояния Θ(k) оцениваемого случайного процесса, получаемых с помощью модели процесса смены состояний ПЗ КВР. Таким образом, данная фаза обучения «с учителем» происходит с помощью согласованных пар входных (значений наблюдений) и эталонных (значений оцениваемого процесса) данных о значениях ПЗ КВР, что означает наличие s независимых друг от друга реализаций случайных векторов на нулевом и k-м шаге анализа защищенности
с совместной функцией плотности распределения вероятности
Во второй, интерактивной, фазе КВР, как предполагается, находятся в процессе реального применения и доступа к ним пользователей, значит, на каждом шаге их эксплуатации и анализа их защищенности происходит адаптивная подстройка весовых коэффициентов АГФ с целью повышения точности оценивания.
В рамках обсуждения полученных шагов анализа необходимо отметить, что в прикладных задачах синтеза алгоритмов фильтрации (включая адаптивную фильтрацию в интересах оперативной оценки защищенности КВР) обязательным этапом является вычисление не только самой оценки, но и адекватной ей расчетной характеристики точности оценивания. В качестве такой характеристики точности для оптимальной в смысле МСКО оценки используется матрица апостериорных дисперсий ошибок оценивания вспомогательных индикаторов состояния Θ(k), вычисляемая с помощью соотношения [21, 22, 24]
.
При разработке классических нейросетевых алгоритмов фильтрации, как правило, не подразумевается получение каких-либо расчетных характеристик точности оценивания. Если для задач оперативной оценки защищенности КВР характеристики точности оценивания важны, АГФ может быть дополнен механизмами вычисления матриц априорных и апостериорных дисперсий ошибок, например для наиболее значимых, важных, специальным образом сгруппированных ПЗ [25]. При этом такая характеристика, аналогичная матрице дисперсий ошибок оценивания, может быть после обучения НСФ для задач оперативной оценки защищенности КВР рассчитана по методу Монте-Карло с использованием выражения [16]
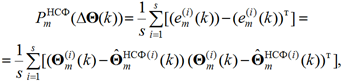
где 
– ошибка оценивания m-го элемента вектора индикаторов состояния защищенности КВР для i-й реализации;
i = 1, …, s – количество независимых друг от друга реализаций случайных элементов 
векторов индикаторов состояния 
значений ПЗ КВР, необходимых для обучения АГФ.
Заключение
Описана математически и показана практическая возможность оперативной оценки защищенности КВР с использованием адаптивной гибридной фильтрации случайных процессов, характеризующих динамику изменения переменных состояния (показателей) защищенности таких ресурсов на определенном временном интервале.
Предложенный подход учитывает неопределенность исходных данных, т. е. априорных сведений о статистике показателей защищенности КВР и шумов наблюдения. Подход базируется на обучаемой искусственной нейронной сети в составе адаптивных фильтров, что, в свою очередь, позволяет подстраивать весовые коэффициенты для процедур фильтрации под статистические характеристики измеряемых и наблюдаемых как линейно, так и нелинейно изменяющихся показателей защищенности критических ресурсов. При этом трудоемкость приведения неопределенных исходных данных к виду, применимому для употребления в используемых аналитических моделях, относительно невелика и связана в основном с затратами ресурсов на обучение искусственной нейронной сети в составе адаптивных фильтров.
Новизна данного подхода, на наш взгляд, заключается в трех важных аспектах – в минимизации вычислительных затрат, в большом объеме учитываемых входных параметров и в условиях неопределенности этих параметров, поскольку ИНС устраняют не все виды неопределенности, включая нечеткость и стохастичность, а претендуют лишь на работу с неполными и противоречивыми исходными данными. Именно этот вид неопределенности, на наш взгляд, более всего соответствует данным наблюдения за ПЗ КВР, измеряемым и наблюдаемым как линейно, так и нелинейно.
Предложены механизмы и описаны стадии обучения нейронной сети в составе адаптивного гибридного фильтра такого класса, рассмотрены подходы для получения расчетных характеристик точности оценивания показателей защищенности.
Практическое применение предложенного подхода к оперативной оценке защищенности КВР возможно как в рамках исследовательских работ, так и в системах автоматизированного контроля защищенности любых ресурсов сложных управляемых промышленных и телекоммуникационных инфраструктур. Направлением дальнейших исследований может быть разработка методов оперативной оценки защищенности, сочетающих гранулярные вычисления и традиционные алгоритмы фильтрации.
1. Котенко И. В., Саенко И. Б. Создание новых си-стем мониторинга и управления кибербезопасностью // Вестн. Рос. акад. наук. 2014. Т. 84, № 11. С. 993-1001.
2. Setola R., Luiijf E., Theoharidou M. Critical Infrastructures, Protection and Resilience // Managing the Complexity of Critical Infrastructures. Springer, 2016. P. 1-18.
3. Kamara M. K. Securing Critical Infrastructures. Bloomington: Xlibris US, 2020. 385 p.
4. Котенко И. В., Паращук И. Б. Информационные и телекоммуникационные ресурсы критически важных инфраструктур: особенности интервального анализа защищенности // Вестн. Астрахан. гос. техн. ун-та. Сер.: Управление, вычислительная техника и информатика. 2022. № 2. С. 33-40.
5. Kotenko I. V., Parashchuk I. B. Description of Information Security Events of Production and Technological Systems Using Fuzzy Graphs // 2022 International Russian Automation Conference (RusAutoCon) (Sochi, Russia, 4-10 September 2022). IEEE Xplore Digital Library: Browse Conferences, 2022. V. (Doc.) 9896271. P. 45-50.
6. Марковская теория оценивания в радиотехнике / под ред. М. С. Ярлыкова. М.: Радиотехника, 2004. 504 с.
7. Arnold R. Cybersecurity: A Business Solution: An executive perspective on managing cyber risk. Winston-Salem: Threat Sketch, LLC, 2017. 100 p.
8. Thill F. Information Security Risk Management // Privacy and Identity Management. Between Data Protection and Security. Privacy and Identity 2021. Springer, Cham. IFIP Advances in Information and Communication Technology. 2022. V. 644. P. 17-22.
9. Ekpo U. Introduction to Cyber Security. Fundamentals. N. Y.: Independently published, 2018. 37 p.
10. NIST Special Publication 800-61. Revision 2 Computer Security Incident Handling Guide, January 16, 2020. URL: https://www.nist.gov/privacy-framework/nist-sp-800-61/ (дата обращения: 28.02.2023).
11. Gabber H. The 2020 CyberSecurity & Cyber Law Guide. N. Y.: Independently published, 2020. 435 p.
12. Allodi L., Cremonini M., Massacci F., Shim W. Measuring the accuracy of software vulnerability assess-ments: experiments with students and professionals // Empirical Software Engineering. 2020. V. 25. P. 1063-1094.
13. Meeuwisse R. Cybersecurity Exposed: The Cyber House Rules. L.: Cyber Simplicity Ltd, 2017. 175 p.
14. Desnitsky V. A., Kotenko I. V., Parashchuk I. B. Neural Network Based Classification of Attacks on Wireless Sensor Networks // 2020 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus) (St. Petersburg and Moscow, 27-30 Janary 2020). IEEE Xplore Digital Library, 2020. P. 284-287.
15. Паращук И. Б., Иванов Ю. Н., Романенко П. Г. Нейросетевые методы в задачах моделирования и анализа эффективности функционирования сетей связи. СПб.: ВАС, 2010. 104 с.
16. Haykin S. O. Adaptive Filter Theory. New Jersey: Prentice Hall Inc., 2002. 920 p.
17. Lo J. T.-H. Synthetic approach to optimal filtering // IEEE Trans. Neural Networks. 1994. V. 5. P. 803-811.
18. Parlos A. G., Menon S. K., Atiya A. F. An algorith-mic approach to adaptive state filtering using recurrent neural networks // IEEE Trans. Neural Networks. 2001. V. 12 (6). P. 1411-1432.
19. Kotenko I. V., Parashchuk I. B. An approach to modeling the decision support process of the security event and incident management based on Markov chains // 9th IFAC Conference on Manufacturing Modelling, Management and Control (MIM 2019) (Berlin, Germany, 28-30 August 2019). IFAC-PapersOnLine. 2019. V. 52. Iss. 13. P. 934-939.
20. Sage A. P., Melsa J. L. Estimation Theory with Ap-plications to Communication and Control. N. Y.: McGraw-Hill, 1971. 752 p.
21. Haykin S. O. Kalman Filtering and Neural Networks. New Jersey: John Wiley & Sons, Inc., 2001. 202 p.
22. Parashchuk I. B. System Formation Algorithm of Communication Network Quality Factors using Artificial Neural Networks // 1st IEEE International Conference on Circuits and Systems for Communications (ICCSC 2002), Proceedings. IEEE Xplore. 2002. P. 263-266.
23. Nerrand O., Roussel-Ragot P., Personnaz L., Dreyfus G., Marcos S. Neural Networks and Non-linear Adaptive Filtering: Unifying Concepts and New Algorithms // Neural Computation. 1993. V. 5 (2). P. 165-197.
24. Kotenko I. V., Parashchuk I. B., Omar T. K. Neuro-Fuzzy Models in Tasks of Intelligent Data Pro-cessing for Detection and Counteraction of Inappropriate, Dubious and Harmful Information // II International Scientific and Practical Conference “Fuzzy Technologies in the Industry” (FTI 2018) (Ulyanovsk, Russia, October 23-25, 2018). CEUR Work-shop Proceedings (CEUR-WS). 2018. V. 2258. P. 116-125.
25. Kotenko I. V., Parashchuk I. B., El Baz D. Selection and justification of information security indicators for materials processing systems // MATEC Web of Conferences. International Conference on Modern Trends in Manufacturing Technologies and Equipment (ICMTMTE 2021) (Sevastopol, Russia, September 6-10, 2021). Published online: 26 October 2021. V. 346 (01019). P. 1-12.
