ФГУП «Атомфлот» (старший помощник капитана)
Россия
Россия
Мурманская область, Россия
УДК 004.9 Прикладные информационные (компьютерные) технологии
В условиях постоянного старения морских судов все сложнее становится обеспечивать их навигационную безопасность. Несмотря на предпринимаемые усилия, человеческий фактор остается основной причиной аварий в морских и речных акваториях. Обоснована необходимость рассмотрения процесса несения ходовой вахты как системы, включающей соответствующие подсистемы. Исследуется система несения ходовой вахты, включающая подсистему самоконтроля человеческого фактора. Составлена модель системы преобразования информации в управлении состоянием безопасности судна, включающая подсистему самоконтроля. Отмечено, что процесс преобразования информации в управлении состоянием судна с самоконтролем способен обеспечить эффективное состояние безопасности судна, экипажа и груза. Введено допущение о том, что время восстановления подсистемы самоконтроля человеческого фактора подчиняется вырожденному закону распределения с определенным математическим ожиданием, что позволит существенно упростить расчетные формулы и создать удобные методики для оценки и обеспечения надежности (безаварийности) в системе несения ходовой вахты. Исследована вероятность безаварийной работы системы несения вахты при вырожденном законе распределения времени восстановления подсистемы самоконтроля человеческого фактора и в случае, когда закон распределения времени восстановления отличен от вырожденного. Проведена оценка вероятности безошибочного преобразования информации с учетом самоконтроля. Рассчитана предельная величина погрешности в вычислении вероятности безаварийной работы системы преобразования информации в управлении при замене любого закона распределения времени восстановления самоконтроля на вырожденный закон распределения. Произведена экспериментальная оценка вероятности надежной работы системы несения ходовой вахты при экспоненциальном законе распределения времени восстановления подсистемы самоконтроля.
законы распределения, восстановление системы, система несения ходовой вахты, безаварийная работа системы, надежность работы системы, преобразования навигационной информации
Introduction
According to expert estimates, the bulk of Russia's civilian fleet consists of heavily depreciated vessels – the average age of vessels exceeds 38 years – requiring special attention to the navigational safety of these vessels. An annual analysis of accidents involving maritime and river transport shows that accidents involving older vessels lead to human casualties and serious environmental consequences. Therefore, it is essential to prioritize ensuring navigational safety and minimizing accidents.
Research shows a disturbing trend: human error often leads to accidents. Fatigue is a particularly pressing issue among seafarers. The most recent widely discussed incident involved a second officer falling asleep on watch, leading to a vessel running aground in Norway, narrowly missing a residential building. In the Russian segment, in July, a tugboat collided with the hull of a cargo ship in the waters of the Nakhodka commercial port. The key cause of the navigational accident was the tugboat captain's fatigue, who fell asleep and lost control of the vessel.
The human factor, coupled with an aging vessel, can lead to serious consequences for vessel safety, confirming the need for further research into the navigational watchkeeping process, considering it as a system with corresponding subsystems. This approach will allow for more comprehensive use of mathematical distribution laws to ensure accident-free navigational watchkeeping.
Thus, the navigational watchkeeping system includes a “human factor” self-monitoring subsystem, i.e., a process of vessel state management with self-monitoring of the conversion of navigational information into control, ensuring the safety of the vessel, crew, and cargo. The self-monitoring subsystem should only be activated in the event of an emergency, so hidden failures are possible during prolonged self-monitoring.
In order to identify hidden failures in the operation of the self-monitoring subsystem with the aim of increasing the reliability of the navigation watch, over time τ at equal time intervals τ0 the decision maker must conduct т sessions of checking the operability and restoration of the self-monitoring subsystem with a duration τВ.
During time τВ the system for converting navigational information into ship control functions without the use of the self-monitoring subsystem. However, an emergency can occur either during the interval τ0, when the self-monitoring subsystem fails and only then will an emergency occur, or when an emergency occurs, with the subsystem being restored again during time τВ.
Further, we will assume that the recovery time of the human factors self-monitoring subsystem obeys a degenerate distribution law with a mathematical expectation М[τВ] = С [1, 2]. This assumption allows us to significantly simplify calculation formulas and create convenient methods for assessing and ensuring the trouble-free operation of the watchkeeping system.
In practice, the recovery time of the self-monitoring subsystem is a random variable that cannot be considered constant [3]. In this regard, it is important to analyze the influence of the distribution of the subsystem recovery time on the probability of trouble-free operation of the watchkeeping system, taking into account the operation of the self-monitoring subsystem. For this purpose, we will compare the probability of trouble-free operation of the watchkeeping system under a degenerate distribution law of the subsystem recovery time with the probability of trouble-free operation of the watchkeeping system under other laws, but with the same mathematical expectation of the subsystem recovery time.
Statement of the problem and basic relationships
Let the failure-free operation time, the failure-free operation time of the self-monitoring subsystem, and the recovery time of the self-monitoring system be random variables in the watchkeeping system (Fig. 1). Furthermore, let F(t) be the distribution function of the failure-free operation time of the system, which is assumed to be exponential; F(t) = 1 – ехр(–λt); FН(t) is the distribution function of the failure-free operation time of the self-monitoring subsystem; FВ(t) is the distribution function of the subsystem recovery time.
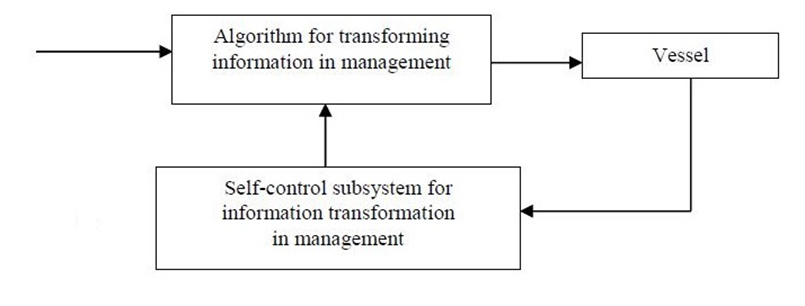
Fig. 1. An algorithm for converting navigation information into ship condition management
with a self-monitoring subsystem
Then, in the system (Fig. 1), the probability of failure-free operation of the watchkeeping system with the self-monitoring subsystem over the time interval from τ1 to τ2, where the times τ1 and τ2 are counted from the start of the watchkeeping, with a degenerate distribution law of the subsystem recovery time, is denoted by P[τ1, τ2].
The following expressions are valid for this probability:
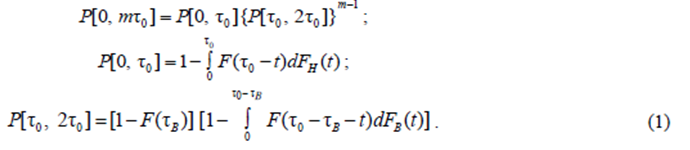
The probability P[τ0, 2τ0] is a function of τВ = С, the recovery time of the self-monitoring subsystem. For convenience, when studying the dependence of Р[τ0, 2τ0] on М[τВ], Р[τ0, 2τ0] will be denoted by Р(М[τВ]) or simply Р(τВ). In the case where the distribution law of the protectionrecovery time FB(t) is non-degenerate, the probability of an accident-free watch with self-monitoring for the time from τ1 to τ2, where the times τ1 and τ2 are counted from the start of the watch, is denoted by Р[τ1 to τ2].
For this probability, the following formulas are valid:
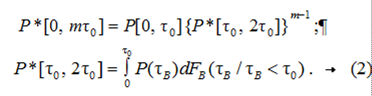
The probability Р*[τ0, 2τ0] is a function of the mathematical expectation М[τB] of the verification time of the process of converting navigation information into controls. We denote this function by P*(М[τB]). In particular, for some specific distribution laws of the failure-free operation time of the self-monitoring subsystem (Fig. 1) and the recovery time of this subsystem, expressions (1) and (2) can be represented as specific, but rather complex dependencies. At the same time, if we denote the function P[0, mτ0] by Pm and the function of the form P*[0, mτ0] by 
, then we can assert that the function Р[0, mτ0] is decreasing with respect to М[τВ].
Further, it can be shown that for any distribution law FB(t) the relative positions of the functions P[0, mτ0] and P*[0, mτ0] with respect to М[τВ] can be determined. For this purpose, it is sufficient to use Jensen's integral formula [4], according to which the following inequality is valid:
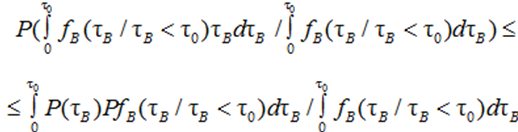
If the function Р(τВ) is convex, then the sign in this inequality is preserved, and if the function Р(τВ) is concave, then the sign in this inequality is reversed. Accordingly, depending on whether the function Р(τВ) is convex or concave, the graphs of 
lie either not below or not above the graph Рm.
Analysis of the function P(τB) for convexity and mutual arrangement
When examining the convexity of the function P(τВ), it is known that the function is convex if its first derivative is increasing, and concave if its first derivative is decreasing.
Having considered various distribution laws, we can conclude that, for any distribution law FB(t), the relative positions of the graphs of the functions Р[0, тτ0] and Р*[0, тτ0] are as follows:
1) if FН(t) = 1 – e–λН is an exponential distribution, then for λ > λН the 
graphs are not located below the Рт graph, for λ = λН the 
graphs and the Рт graph coincide, and for λ < λН the
graphs are not located above the Рт graph;
2) if FН(t) = 1 – (2t / TН)e–2t/TН – e–2t/TН is the first order Erlang distribution, then the 
graphs are located not lower than the Рт graph when
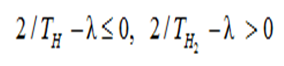
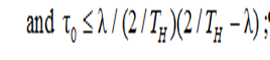
3) if FН(t) = 1 – е–βt, α, β > 0 is the Weibull distribution, then the 
graphs are located not lower than the Рт graph when
;
4) if 
(α is an integer) is a gamma distribution, then the
graphs are located not lower than the Рт graph when λ ≤ 1 / β.
For the second and third cases, with parameter relationships not considered above, the function Р(τВ) is neither convex nor concave. With such parameter relationships, the graphs of 
and Рт may intersect.
In the fourth case, the inequality λ ≥ 1 / β is only a sufficient condition for the convexity of the function Р(τВ). For λ < 1 / β, the analytical expressions obtained when examining the convexity of the function Р(τВ) are so cumbersome that their practical use is impossible.
It should be noted here that the Rayleigh distribution law can be considered as a special case of the Weibull distribution law for α = 2, and β = 1 / 2σ2 [5, 6]. Consequently, the considered basic distribution laws, for which the study of the function Р(τВ) for convexity yields fairly simple analytical expressions. In other cases (as, for example, for the normal distribution law), the study can only be carried out by a numerical method.
Estimation of the probability of error-free transformation of information taking into account self-monitoring
The conducted analysis of the convexity conditions of the Р(τВ) function allows us to formulate a methodology for assessing the probability of reliable operation of the navigation information conversion system in managing the state of ship navigation safety under any distribution law of the self-monitoring subsystem recovery time.
The probability of error-free operation of the information conversion system in control with the self-monitoring subsystem over time mτ0 can be found using the approximate expression
,
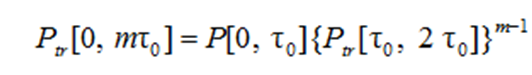where
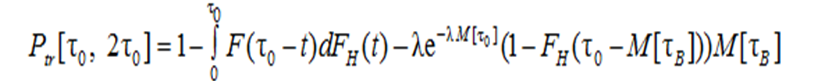
with an error Δ, not exceeding the value:
– for a degenerate distribution law
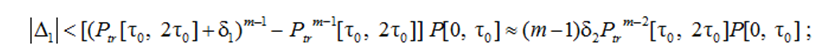
– for any other distribution law
,
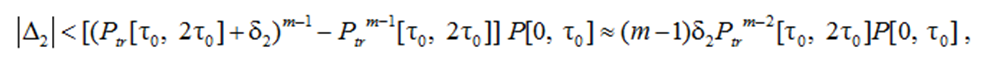where
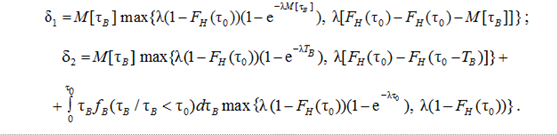
In this case, the error Δ3 in calculating the probability of trouble-free operation of the information conversion system in control over time mτ0 when replacing any distribution law of the self-control recovery time τВ with a degenerate distribution law will not exceed the value
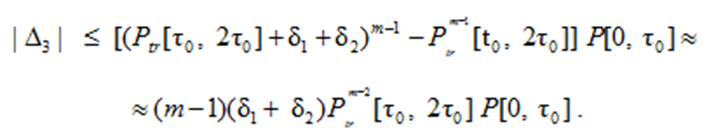
Experimental assessment of the reliability of the navigational watchkeeping system
We will conduct an experimental assessment of the probability of reliable operation of the navigation information conversion system in managing the ship's navigational safety status with an exponential distribution of the self-monitoring subsystem recovery time. The initial data was analyzed over 100 hours of watchkeeping, which included twenty-five watches, with hidden failures of the self-monitoring subsystem occurring during eight watches. To construct a statistical series, the total watchkeeping time (100 hours) was divided into ten intervals (categories) of 10 hours each for each categorization. A histogram of the probability of failure of the self-monitoring subsystem of the watchkeeping system is shown in Fig. 2.
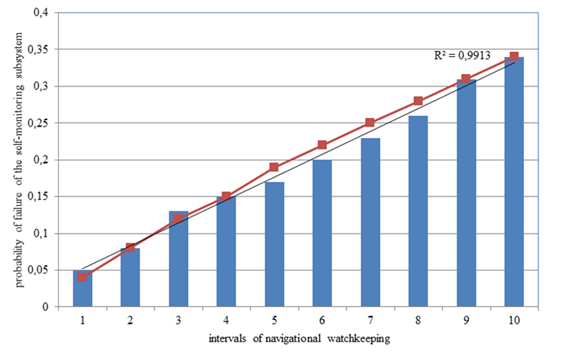
Fig. 2. Histogram of the probability of failure of the self-monitoring subsystem
of the navigation watch system
The calculated coefficient of determination (0.99) indicates a very high degree of data conformity with the model, i.e., the model explains their variation almost perfectly. Thus, the exponential distribution model of the self-monitoring subsystem's recovery time can be used for an a priori analysis of the reliability of watchkeeping, which is important for voyage planning and ensuring navigational safety.
Conclusion
For information conversion systems in control, the probability of error-free operation of this system with a degenerate self-monitoring recovery time distribution law is the lower or upper limit of the probability of error-free operation of the entire system with any other self-monitoring recovery time distribution law. The error in calculating the probability of error-free operation of a conversion system with self-monitoring when replacing an exact formula with an approximate one, or any self-monitoring recovery time distribution law with a degenerate law, is insignificant and can practically be ignored altogether. When developing methods for assessing and ensuring the reliability of information conversion systems, taking into account the use of self-monitoring subsystems, it is practically possible to use any self-monitoring recovery time distribution that allows for simplifying the calculation formulas.
1. Заренин Ю. Г., Збырко М. Д. О надежности систем с защитой // Техн. кибернетика. 1971. № 2. С. 46–52.
2. Надежность и эффективность АСУ / под ред. Ю. Г. Зарезина. Киев: Технiка, 1975. 368 с.
3. Позняков С. И., Меньшиков В. И. Методы разре-шения нештатных ситуаций при управлении судовыми технологическими процессами. Мурманск: Изд-во МГТУ, 2017. 184 с.
4. Збырко М. Д., Кузнецов В. Н., Вовкодав Н. Г. Надежность. Методы аналитической оценки надежности систем с защитой. Киев: Изд-во Ин-та автоматики, 1981. 268 с.
5. Фихтенголъц Г. М. Курс дифференциального и интегрального исчисления. М.: Наука, 1966. Т. 2. 800 с.
6. Шубинский И. Б. Функциональная надежность информационных систем. Методы анализа. М.: Журн. «Надежность», 2012. 296 с.
