Россия
Представлены алгоритмы численного расчета кинетических параметров процесса вулканизации по двум методам. Так как кинетические параметры вулканизации сильно зависят от рецептуры резиновой смеси, в исследовании рассматривались две смеси с разным составом. Для описания кинетики протекания вулканизации используется представление о том, что процесс состоит из трех реакций первого порядка: образования стабильных связей между макромолекулами каучука, образования нестабильных связей и разрушения нестабильных связей (реверсии). Константы скоростей этих реакций описываются уравнением Аррениуса. Алгоритмы расчета включают анализ экспериментальных кривых реометра, определение кинетических параметров индукционного периода, расчет кинетических параметров трех реакций, проверку найденных параметров путем численного моделирования изотермической вулканизации при разных температурах. Отличие двух подходов к расчету кинетических параметров заключается в определении предэкспоненциальных множителей и энергий активации уравнений Аррениуса. Согласно первому подходу, сначала определяются константы скоростей реакций, затем по ним находятся предэкспоненциальные множители и энергии активации. Во втором варианте непосредственное определение констант скоростей реакций не требуется. Установлено, что для резиновой смеси, не склонной к реверсии, оба подхода приводят к незначительной погрешности. Расчет кинетических параметров для резиновой смеси, имеющей ярко выраженный период реверсии, дает большую погрешность в обоих случаях, что свидетельствует о сложности моделирования реверсии. На основе проведенного исследования сделан вывод о необходимости поправочного коэффициента при расчете экспериментальной степени вулканизации по показаниям реометра. Также требуется разработка ограничений при поиске оптимальных кинетических параметров.
вулканизация, резинотехнические изделия, математическое моделирование, кинетика, реверсия, резиновая смесь
Введение
Производство качественной резинотехнической продукции представляет сложность ввиду низкой теплопроводности резиновых смесей. Основным этапом, на котором будущему изделию придаются форма и эксплуатационные свойства, является вулканизация. Пресс-форма с резиновой смесью нагревается до заданной температуры и под давлением выдерживается определенное время, после чего изделие извлекается и остывает на воздухе. При этом процесс вулканизации протекает в три стадии (рис. 1) [1]:
1) индукционный период: резиновая смесь сохраняет вязкотекучее состояние и приобретает форму детали, при этом реакция вулканизации отсутствует;
2) период вулканизации: характеризуется увеличением крутящего момента из-за сшивания молекул каучука друг с другом и образования пространственной сетки;
3) период реверсии: нестабильные связи между молекулами каучука распадаются, что сопровождается ухудшением механических свойств резины.
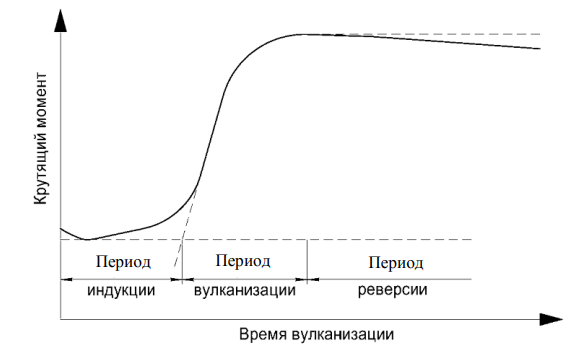
Рис. 1. Кинетическая кривая процесса вулканизация
Fig. 1. Kinetic curve of the vulcanization process
Из-за неравномерного прогрева резиновой смеси в отдельных областях изделия вулканизация протекает неодновременно: когда в наиболее нагретых зонах начинается реверсия, в других частях процесс вулканизации может еще не начаться. С увеличением толщины изделия эта проблема становится более существенной и значительно усложняется задача подбора режимных параметров (температуры и времени выдержки изделия в пресс-форме). Моделирование процесса вулканизации позволит значительно сократить затраты времени и материалов на подбор оптимальных режимов процесса и проектирование пресс-форм для производства новых резинотехнических изделий. Разработкой методов численного моделирования процесса вулканизации занимаются многие современные ученые из разных стран [1–11]. Однако в российской научной литературе данный вопрос недостаточно освещен. Основная трудность моделирования процесса вулканизации заключается в том, что на данный момент нет единой математической модели, достоверно описывающей этот процесс. В зависимости от состава резиновой смеси изменяется протекание процесса вулканизации. По этой причине уравнения, хорошо описывающие вулканизацию для одних резиновых смесей, совершенно не подходят для описания процесса вулканизации других смесей. Также актуальным остается вопрос моделирования периода реверсии.
Целью данного исследования является сравнение двух методов расчета параметров кинетических уравнений процесса вулканизации различных резиновых смесей.
Математическое описание кинетики вулканизации
Длительность периода индукции (см. рис. 1) определяется по формуле [6]
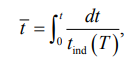
где 
– безразмерное время, которое принимает значение 1, когда заканчивается индукционный период и начинается вулканизация; tind(T) – зависимость времени индукционного периода от температуры Т, с.
Длительность индукционного периода определяется уравнением Аррениуса:
(1)
где t0 – предэкспоненциальный множитель, с–1; e – основание натурального логарифма; Eind – энергия активации периода индукции, Дж/моль; Т – температура, К; R – универсальная газовая постоянная, Дж/(моль·К).
По окончании индукционного периода начинается этап вулканизации, завершающийся реверсией (см. рис. 1). В работе [12] предлагается рассматривать процесс вулканизации как совокупность трех реакций первого порядка (рис. 2).
Рис. 2. Схема реакции вулканизации: образование стабильных связей (с1),
образование нестабильных связей (с2) и разрушение нестабильных связей (p); S – сера; k1, k2, k3 – константы
скоростей протекания реакций образования стабильных связей, образования нестабильных связей
и разрушения нестабильных связей соответственно
Fig. 2. Scheme of vulcanization reaction: formation of stable bonds (с1),
formation of unstable bonds (с2) and destruction of unstable bonds (p); S – sulfur; k1, k2, k3 – rate constants of reactions
of formation of stable crosslinks, formation of unstable crosslinks and destruction of unstable crosslinks, respectively
В работах [13, 14] используется система дифференциальных уравнений для описания кинетики процесса вулканизации согласно схеме, представленной на рис. 2:
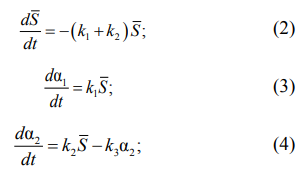
где 
– доля серы, доступной для образования связей (меняется от 1 до 0); k1–k3 – константы скоростей реакций, c–1 (см. рис. 2); α – глобальная степень вулканизации; α1, α2 – степени вулканизации, соответствующие реакциям образования стабильных и нестабильных связей.
Аналитическое решение системы уравнений (2)–(5), предложенное в статье [13], позволяет вычислить глобальную степень вулканизации при изотермическом протекании процесса:
(6)
где текущее время t больше времени индукции tind. При t < tind степень вулканизации α = 0.
Константы скоростей реакций k1, k2, k3 (см. рис. 2) при этом определяются уравнением Аррениуса [14]:
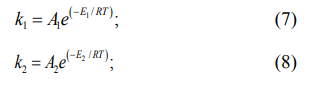
где А1–А3 – предэкспоненциальные множители реакций, с–1; Е1–Е3 – энергии активаций реакций, Дж/моль.
Чтобы определить параметры, необходимые для моделирования кинетики вулканизации, требуются экспериментальные данные изотермического протекания процесса. В данной работе для сравнения используются экспериментальные данные из работы [7] и собственные данные, полученные для резиновой смеси производства России на основе натурального каучука.
Определение кинетических параметров
Параметры, необходимые для численного моделирования кинетики вулканизации, определялись по двум методам, описанным в работе [14], после чего производилась проверка найденных значений путем сравнения численного расчета кинетики вулканизации с экспериментальными данными.
В рассматриваемых методах определение t0 и Eind осуществляется путем построения графика линейной зависимости lntind (1 / Т) (рис. 3):
B =lnt0; (10)
, (11)
где B – ордината пересечения аппроксимирующей прямой с вертикальной осью; φ – угол наклона аппроксимирующей прямой.
Рис. 3. График для определения Еind и t0
Fig. 3. Graph for determining Eind and t0
Далее по первому методу определяются константы трех реакций k1–k3 методом наименьших квадратов:
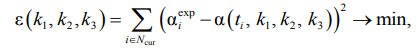(12)
где ε – сумма квадратов отклонений расчетной степени вулканизации от экспериментальной; Ncur– множество экспериментальных точек периодов вулканизации и реверсии; 
– степень вулканизации, полученная из изотермического эксперимента; ti – время, с; α(ti, k1, k2, k3) – степень вулканизации, найденная по уравнению (6). Для функции (12) характерно большое количество локальных минимумов, поэтому следует использовать методы глобальной оптимизации. В данной работе применялся метод мультистарта, поиск локальных экстремумов осуществлялся по методу сопряженных градиентов.
Получение экспериментальных значений степени вулканизации осуществляется путем преобразования значений крутящих моментов по формуле [5]:
, (13)
где Мi, Мmin, Мmax – текущий, минимальный и максимальный крутящие моменты соответственно, Н·м.
Затем строятся графики линейной зависимости lnk1, lnk2 и lnk3 от 1 / Т для определения параметров А1–А3, Е1–Е3 из уравнений (7)–(9) аналогично рис. 3.
Второй метод основывается на изоконверсионном анализе [15], при котором кинетическое уравнение вулканизации представляется в виде
, (14)
где Аα – кажущийся предэкспоненциальный множитель; Eα – кажущаяся энергия активации; f(α) – функция, описывающая кинетику вулканизации.
В случае простой реакции Аα и Eα являются константами, следовательно, можно проинтегрировать уравнение (14) для изотермического процесса, тогда [14]
, (15)
где 
– время, при котором степень вулканизации принимает значение α = αj при определенной температуре Ti.
Таким образом, мы можем определить значение Eα как наклон графика линейной зависимости 
от 1 / RTi. При этом не учитывается период индукции, поэтому кажущаяся энергия активации определяется зависимостью от 1 / RTi. Затем энергии активаций из уравнений (7), (8) принимаются равными среднему значению найденных кажущихся энергий активаций. Энергия активации, входящая в уравнение (9), определяется аналогично, но в этом случае рассматривается только период реверсии, определяется наклон графика 
от 1 / RTi.
Зная энергии активации Е1–Е3, определяем А1–А3 методом наименьших квадратов по формуле (12) для одной любой температуры.
Последним этапом в обоих методах является проверка найденных кинетических параметров путем сравнения экспериментальных кривых изменения степени вулканизации с кривыми, полученными в результате численного моделирования. Для этого систему дифференциальных уравнений (2)–(5) решаем с использованием метода Рунге – Кутта четвертого порядка.
Алгоритмы расчета по двум рассматриваемым методам представлены на рис. 4.
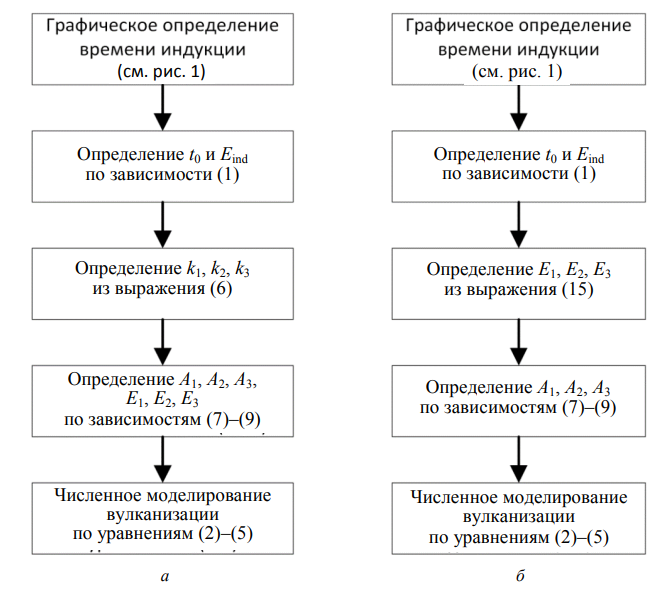
Рис. 4. Алгоритм расчета кинетических параметров вулканизации: а – метод 1; б – метод 2
Fig. 4. Algorithm for calculating kinetic parameters of vulcanization: a – method 1; б – method 2
Результаты и их обсуждение
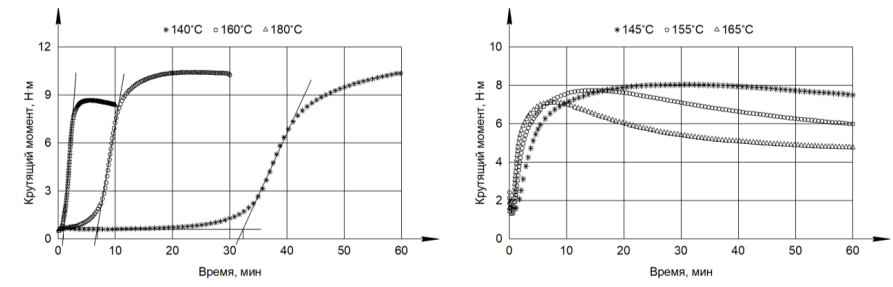
Определение кинетических параметров выполнялось для экспериментальных данных из работы [7] (рис. 5, а) и данных, полученных для резиновой смеси российского производства (рис. 5, б).
а б
Рис. 5. Реометрические кривые: а – зарубежная резиновая смесь; б – резиновая смесь российского производства
Fig. 5. Rheometric curves: a – foreign rubber compound; б – Russian-made rubber compound
Таким образом (см. рис. 5), состав резиновой смеси оказывает сильное влияние на кинетику процесса вулканизации. Кинетика вулканизации резиновой смеси на основе натурального каучука российского производства имеет ярко выраженный период реверсии, что делает задачу численного моделирования более актуальной.
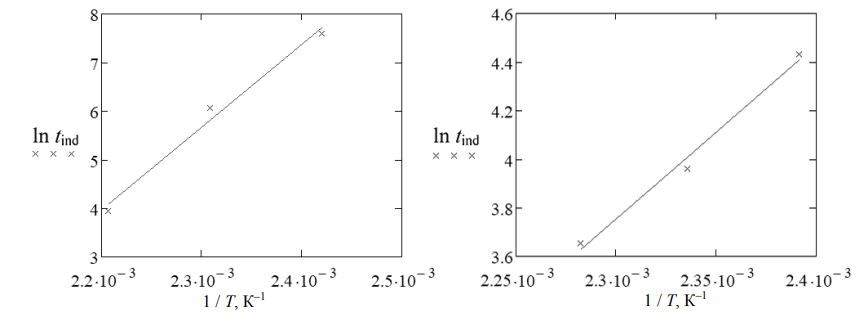
На рис. 6 представлены графики для определения t0 и Eind.
а б
Рис. 6. Определение кинетических параметров периода индукции:
а – зарубежная резиновая смесь; б – резиновая смесь российского производства
Fig. 6. Determination of kinetic parameters of the induction period:
a – foreign rubber compound; б – Russian-made rubber compound
По графикам (см. рис. 6) были найдены следующие кинетические параметры периода индукции:
– смесь из работы [7]: t0 = 2,6754 · 10–15 и Eind = = 1,41777 · 105;
– смесь российского производства: t0 = 3,1017 · 10–6 и Eind = 5,94195 · 104.
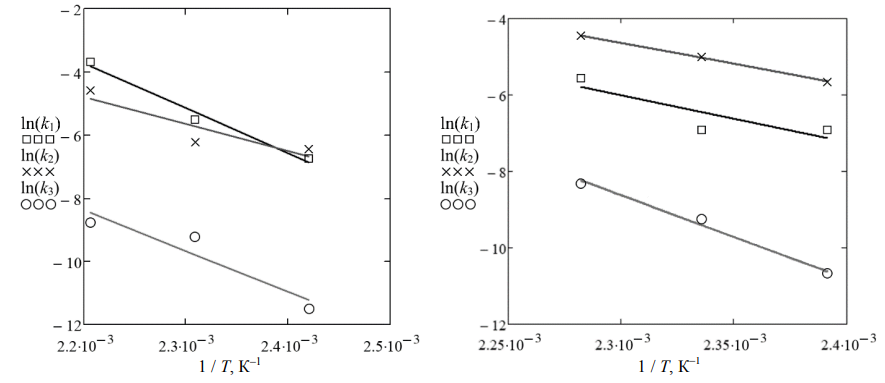
На рис. 7 представлены графики определения k1–k3 по первому методу; после определения кинетических параметров осуществлялся проверочный расчет с использованием метода Рунге – Кутты четвертого порядка (рис. 8).
а б
Рис. 7. Определение констант скоростей реакций:
а – зарубежная резиновая смесь; б – резиновая смесь российского производства
Fig. 7. Determination of reaction rate constants:
a – foreign rubber compound; б – Russian-made rubber compound
а б
Рис. 8. Проверочный расчет для первого метода:
а – зарубежная резиновая смесь; б – резиновая смесь российского производства
Fig. 8. Verification calculation for the first method:
a – foreign rubber compound; б – Russian-made rubber compound
Определение кинетических параметров по первому методу (см. рис. 8) дает хорошие результаты для резиновой смеси из работы [7], однако приводит к значительным погрешностям при численном моделировании кинетики вулканизации российской смеси.
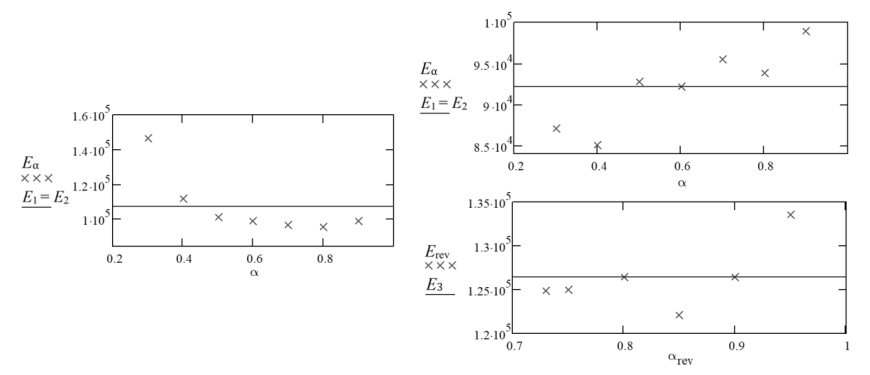
Согласно второму методу мы непосредственно определяем значения предэкспоненциальных множителей и энергий активаций для трех реакций первого порядка, описываемых выражениями (7)–(9). На рис. 9 представлено определение энергии активации по второму методу.
а б
Рис. 9. Кажущиеся энергии активации: а – зарубежная резиновая смесь;
б – резиновая смесь российского производства
Fig. 9. Apparent activation energies: a – foreign rubber compound; б – Russian-made rubber compound
Как описано в работе [14], принимаем E1 = E2 и определяем как среднее значение найденных кажущихся энергий активаций периода вулканизации (см. рис. 9). Е3 определяется аналогично, но в этом случае рассматривается период реверсии, который для экспериментальных данных из работы [7] отсутствует, поэтому для дальнейшего расчета принято Е3 = 1,85E1. После определения Е1–Е3 рассчитываем А1–А3 по формуле (12) с температурами 140 и 145 °С для экспериментальных данных из работы [7] и данных, полученных для резиновой смеси российского производства, соответственно. Проверочный расчет с использованием метода Рунге – Кутты четвертого порядка представлен на рис. 10; рассчитанные по двум методам кинетические параметры приведены в таблице.
а б
Рис. 10. Проверочный расчет для второго метода:
а – зарубежная резиновая смесь; б – резиновая смесь российского производства
Fig. 10. Verification calculation for the second method:
a – foreign rubber compound; б – Russian-made rubber compound
Параметры кинетических уравнений
Parameters of kinetic equations
|
Параметр |
Резиновая смесь из работы [7] |
Российская смесь |
||
|
Метод 1 |
Метод 2 |
Метод 1 |
Метод 2 |
|
|
Период индукции |
||||
|
t0, c |
1,984 · 10–12 |
3,1017 · 10–6 |
||
|
Eind, Дж/моль |
1,187 · 105 |
5,94195 · 104 |
||
|
Вулканизация |
||||
|
А1, с–1 |
1,028 · 1012 |
1,882 · 107 |
5,594 · 109 |
1,473 · 109 |
|
E1, Дж/моль |
1,186 · 105 |
1,069 · 105 |
1,028 · 105 |
9,221 · 104 |
|
А2, с–1 |
1,125 · 106 |
8,919 · 1010 |
2,031 · 109 |
4,675 · 107 |
|
E2, Дж/моль |
7,080 · 104 |
1,069 · 105 |
9,414 · 104 |
9,221 · 104 |
|
Реверсия |
||||
|
А3, с–1 |
5,171 · 108 |
9,995 · 1016 |
1,034 · 1018 |
4,877 · 1013 |
|
E3, Дж/моль |
1,075 · 105 |
1,977 · 105 |
1,811 · 105 |
1,264 · 105 |
Как видно из рис. 10, второй метод также приводит к большим погрешностям при моделировании кинетики вулканизации резиновой смеси с ярко выраженным периодом реверсии.
Выводы
На основе проведенного исследования были выявлены следующие причины, приводящие к неточностям численного моделирования:
1. При обработке экспериментальных данных по формуле (13) значение степени вулканизации достигает 1, что противоречит модели (см. рис. 2). Для решения этой проблемы предлагается ввести в выражение (13) поправочный коэффициент.
2. При определении кинетических параметров, в частности констант скоростей реакций k1–k3, методом наименьших квадратов целевая функция имеет множество локальных минимумов, которые близки по значениям. По этой причине представляется целесообразным разработка ряда ограничений, которые необходимо учитывать при поиске кинетических параметров процесса вулканизации.
3. Численное моделирование периода реверсии представляет значительные трудности. Несмотря на большое количество публикаций по моделированию процесса вулканизации резиновых смесей, вопрос изучения реверсии остается актуальным.
Дальнейшие исследования будут направлены на разработку математической модели, достоверно описывающей кинетику вулканизации российских резиновых смесей с учетом периода реверсии.
1. Pianese G., Milani G., Milani F. Kinetic mathematical model with induction and reversion for the vulcanization of natural rubber and ethylene propylene diene monomer blend // Polym. Test. 2024. V. 131. P. 108339. DOI:https://doi.org/10.1016/j.polymertesting.2024.108339.
2. Tikhomirov S. G., Pyatakov Y. V., Karmanova O. V., Maslov A. A., Khaustov I. A., Podval’nyi S. L. A Technique of Calculating the Kinetics of the Process of Nonisothermal Vulcanization of Large Articles // Chem. Pet. Eng. 2018. V. 53. N. 9–10. P. 647–652. DOI:https://doi.org/10.1007/s10556-018-0396-0.
3. Ghoreishy M. H. R. A state-of-the-art review on the mathematical modeling and computer simulation of rubber vulcanization process // Iran. Polym. J. 2016. V. 25. N. 1. P. 89–109. DOI:https://doi.org/10.1007/s13726-015-0405-5.
4. Lubura J., Kojić P., Pavličević J., Ikonić B., Balaban D., Bera O. A Novel Approach for Simulation and Optimization of Rubber Vulcanization // Polymers (Basel). 2023. V. 15. N. 7. P. 1750. DOI:https://doi.org/10.3390/polym15071750.
5. Bera O., Pavličević J., Ikonić B., Lubura J., Govedarica D., Kojić P. A new approach for kinetic modeling and optimization of rubber molding // Polym. Eng. Sci. 2021. V. 61. N. 3. P. 879–890. DOI:https://doi.org/10.1002/pen.25636.
6. Chen M., Zhou Y., Shen Z., Liu J., Gao R., Li X., Zhang L., Li F. A crosslinking kinetic model considering reversion effect with verification and its application in thick rubber vulcanization process // Polymer (Guildf). 2023. V. 287. P. 126443. DOI:https://doi.org/10.1016/j.polymer.2023.126443.
7. Lopes H., Silva S. P., Carvalho J. P., Machado J. A new modelling approach for predicting process evolution of cork-rubber composites slabs vulcanization // Sci. Rep. 2022. V. 12. N. 1. P. 8002. DOI:https://doi.org/10.1038/s41598-022-11849-7.
8. Adam Q., Behnke R., Kaliske M. A thermo-mechanical finite element material model for the rubber forming and vulcanization process: From unvulcanized to vulcanized rubber // Int. J. Solids Struct. 2020. V. 185–186. P. 365–379. DOI:https://doi.org/10.1016/j.ijsolstr.2019.08.037.
9. Ebel W., Nikanorov A., Baake E. Numerical modelling of induction heated multi-zones rubber vulcanization process // COMPEL - Int. J. Comput. Math. Electr. Electron. Eng. 2017. V. 36. N. 2. P. 497–503. DOI:https://doi.org/10.1108/COMPEL-05-2016-0241.
10. Gong L., Yang H., Ke Y., Wang S., Yao X. Investigation on vulcanization degree and residual stress on fabric rubber composites // Compos. Struct. 2019. V. 209. P. 472–480. DOI:https://doi.org/10.1016/j.compstruct.2018.10.089.
11. Тихомиров С. Г., Маслов А. А., Карманова О. В., Хаустов И. А., Линцова Е. В., Олейник А. С. Программное обеспечение для исследования процессов вулканизации полимерных композиций с помощью математического моделирования // Вестн. Тамб. гос. техн. ун-та. 2022. Т. 28. № 4. С. 544–558. DOI:https://doi.org/10.17277/vestnik.2022.04.pp.544-558.
12. Sun X., Isayev A. I. Cure Kinetics Study of Unfilled and Carbon Black Filled Synthetic Isoprene Rubber // Rubber Chem. Technol. 2009. V. 82. N. 2. P. 149–169. DOI:https://doi.org/10.5254/1.3548241.
13. Han I. S., Chung C. B., Kang S. J., Kim S. J., Jung H. C. A kinetic model of reversion type cure for rubber compounds // Polym. Korea. 1998. V. 22. N. 2. P. 223–230.
14. Leroy E., Souid A., Deterre R. A continuous kinetic model of rubber vulcanization predicting induction and reversion // Polym. Test. 2013. V. 32. N. 3. P. 575–582. DOI:https://doi.org/10.1016/j.polymertesting.2013.01.003.
15. Sbirrazzuoli N. Advanced isoconversional kinetic analysis: Insight in mechanisms and simulations. Successes and future // Thermochim. Acta. 2024. V. 733. P. 179688. DOI:https://doi.org/10.1016/j.tca.2024.179688.
