Россия
Россия
Россия
УДК 004.421 Алгоритмы составления программ
В условиях стремительной цифровой трансформации бизнеса экономические подразделения сталкиваются с необходимостью пересмотра традиционных подходов к организации труда. Возрастающая сложность бизнес-процессов и динамичная конкурентная среда требуют внедрения инновационных решений, которые позволяют обеспечить устойчивое конкурентное преимущество. Представлена методика, основанная на применении генетических алгоритмов для оптимизации распределения задач между сотрудниками. Данный подход позволяет достичь принципиально нового уровня управления, учитывающего как объективные параметры задач и сотрудников, так и динамику изменений в рабочей среде. Ключевым преимуществом предложенной методики является ее адаптивность: система способна оперативно реагировать на изменения приоритетов, доступности ресурсов и других рабочих условий. Механизмы естественного отбора и генетических комбинаций обеспечивают сбалансированное распределение нагрузки, которое учитывает профессиональные компетенции и текущую занятость сотрудников. Это позволяет минимизировать риски перегрузки отдельных работников и повысить общую продуктивность команды. Особенностью данного решения является сочетание автоматизированного анализа данных с возможностью экспертной корректировки. Руководитель получает рекомендации по распределению задач, сохраняя при этом контроль над процессом и учитывая неформальные аспекты работы коллектива. Такой подход не только повышает эффективность выполнения задач, но и способствует созданию более гармоничной и продуктивной рабочей атмосферы. В результате внедрения данной методики компании могут значительно улучшить свои операционные показатели и успешно адаптироваться к изменениям в бизнес-среде, что в конечном итоге приводит к укреплению их позиций на рынке.
генетический алгоритм, распределение задач, оптимизация рабочего процесса, вычислительные методы, компоненты генетических алгоритмов, метод отбора хромосомы, экономический отдел
Введение
Современные экономические отделы сталкиваются с возрастающей сложностью управления операционной деятельностью. Поток задач включает различные операции – от первичной обработки документации до формирования комплексной отчетности, каждая из которых требует соблюдения жестких регламентов и наличия специализированных компетенций, обеспечивающих корректное решение задачи. Традиционные способы распределения рабочей нагрузки путем фрагментарного назначения задач или неформализованных договоренностей между сотрудниками демонстрируют свою неэффективность в условиях роста объемов работы и ужесточения требований [1]. В таких условиях на первый план выходит необходимость внедрения системного подхода к управлению операционными процессами. Речь идет не только о цифровизации рутинных операций, но и о создании прозрачных механизмов распределения задач с учетом компетенций сотрудников, загрузки и приоритетов. Важным элементом становится автоматизация контроля исполнения, позволяющая минимизировать человеческий фактор и обеспечить соблюдение регламентов на каждом этапе работы.
Существующие методики распределения задач
Среди многообразия подходов к распределению задач особого внимания заслуживают методики, основанные на принципах гибкого управления. Одной из наиболее эффективных является система планирования, заимствованная из методологии Scrum и адаптированная под специфику финансовой деятельности [2]. Scrum как методология управления задачами представляет собой гибкий подход, основанный на принципах адаптивного планирования и поэтапной реализации работ. В контексте деятельности экономического отдела Scrum предлагает структурированный, но при этом достаточно гибкий механизм организации рабочих процессов, позволяющий эффективно реагировать на изменения приоритетов и внешних условий.
Сущность Scrum-методологии заключается в разделении рабочего процесса на фиксированные временные циклы, называемые спринтами. Продолжительность этих циклов может варьироваться. Каждый спринт начинается с этапа планирования, где определяются задачи, которые необходимо выполнить в текущем цикле, и заканчивается подведением итогов, включающим анализ достигнутых результатов и выработку решений по улучшению рабочих процессов. Ключевой особенностью Scrum является четкое распределение ролей среди участников рабочего процесса. В экономическом отделе это может выражаться в назначении сотрудника, выполняющего функции Product Owner, специалиста, отвечающего за создание и развитие продукта, а также за формирование и приоритезацию перечня задач, и Scrum Master, обеспечивающего соблюдение методологии и устранение препятствий в работе команды [3]. Остальные сотрудники отдела образуют рабочую группу, совместно отвечающую за выполнение поставленных задач. Практическое применение данной методики находит свое отражение в специализированных системах управления задачами, таких как Jira [4].
В контексте работы экономического отдела Jira позволяет структурировать рабочий процесс следующим образом: все поступающие задачи фиксируются в единой системе, где они классифицируются по типам, срочности и важности. Руководитель отдела или назначенный ответственный сотрудник регулярно проводит переоценку приоритетов, учитывая как стратегические цели компании, так и оперативную ситуацию. Особенностью использования Jira в экономических отделах является необходимость адаптации стандартных подходов к специфике финансовой деятельности. В отличие от IT-сферы, где изначально применялась данная методология, работа экономистов требует учета нормативных сроков сдачи отчетности, периодичности выполнения тех или иных операций, а также сезонных колебаний нагрузки. Поэтому в настройках системы важно предусмотреть соответствующие параметры и фильтры, позволяющие оперативно реагировать на изменения внешних условий.
Несмотря на преимущества Scrum и Jira в управлении проектами, их внедрение в экономических отделах сталкивается с рядом существенных ограничений. Основная сложность заключается в несоответствии жесткой цикличности Scrum непрерывному характеру финансовых процессов. Экономические отделы работают в условиях постоянного потока оперативных задач – от обработки платежей до подготовки срочной отчетности, что делает фиксированные спринты искусственным и неудобным инструментом планирования.
Jira, изначально разработанная для IT-команд, требует значительной адаптации под финансовую специфику. В экономических отделах задачи часто взаимосвязаны нормативными сроками, законодательными требованиями и сложными последовательностями операций. Стандартные доски Jira не всегда отражают эти зависимости, что приводит к ошибкам в планировании. Еще одна проблема – избыточная детализация задач, которая может замедлять работу вместо ее оптимизации. Экономистам важнее быстро решить вопрос, чем тратить время на оформление карточек и оценку эффективности выполнения конкретной задачи. Перспективным представляется внедрение математических методов. Среди существующих подходов можно выделить методы линейного программирования, эффективные для задач с четкими ограничениями, теорию игр, полезную при наличии конкурирующих приоритетов, а также методы имитационного моделирования, позволяющие анализировать сложные процессы с высокой степенью неопределенности. Наиболее перспективными в данном контексте являются генетические алгоритмы, поскольку данный метод разработан для поиска эффективных решений в сложных условиях с большим количеством взаимозависимых факторов и высокой динамикой изменений.
Компоненты генетических алгоритмов для планирования рабочих задач
Генетический алгоритм предлагает новый способ организации рабочего процесса, при котором распределение задач происходит не линейно, а через многовариантное моделирование возможных сценариев [5]. Алгоритм учитывает не только очевидные факторы вроде сроков выполнения и квалификации сотрудников, но и менее формализуемые аспекты: историческую эффективность работы с определенными типами задач, психологическую совместимость участников рабочих групп, динамику изменения приоритетов.
Ключевыми компонентами являются:
1. Популяция (совокупность) – набор потенциальных решений проблемы. В рамках рассматриваемой предметной области – набор возможных способов распределения задач между сотрудниками, например:

Каждое решение – уникальный и потенциальный способ распределения задач.
2. Хромосома – одно решение, представленное в виде последовательности генов. При планировании рабочих задач хромосома представляет собой полный план распределения задач. Хромосома для команды из 3 сотрудников и 3 задач представлена следующим образом:
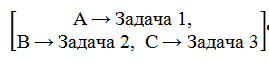
3. Ген – компонент хромосомы, который кодирует часть решения [6]. При планировании задач ген кодирует, какой сотрудник назначен для выполнения конкретной работы. В представленной выше хромосоме гены будут распределены следующим образом:
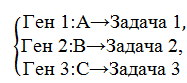
Каждый из генов вносит свой вклад в общее решение, т. е. в хромосому.
4. Функция пригодности – показатель, который оценивает качество решения. Оценивает такие факторы, как время выполнения задачи, баланс рабочей нагрузки и общая удовлетворенность сотрудников. Например, хромосома, представленная в примере, может получить высокий балл пригодности, если:
– сотрудник А, обладающий необходимыми навыками, быстро выполнит задачу 1, т. е. время выполнения будет минимальным;
– рабочая нагрузка равномерно распределена между сотрудниками, т. е. задачи 1, 2 и 3 имеют одинаковую сложность для соответствующих сотрудников.
5. Селекция (отбор) – выбор наилучших решений, которые послужат «родителями» для следующих поколений, что гарантирует сохранение и совершенствование высококачественных решений [7]. Для популяции из 10 хромосом выбраны 3 лучших решения в качестве родителей на основе высокого показателя пригодности:

Данные родители будут использованы для создания «потомства», т. е. станут основой для наиболее благоприятных решений [8].
Одним из распространенных методов выбора является пропорциональный отбор, представленный на рис.
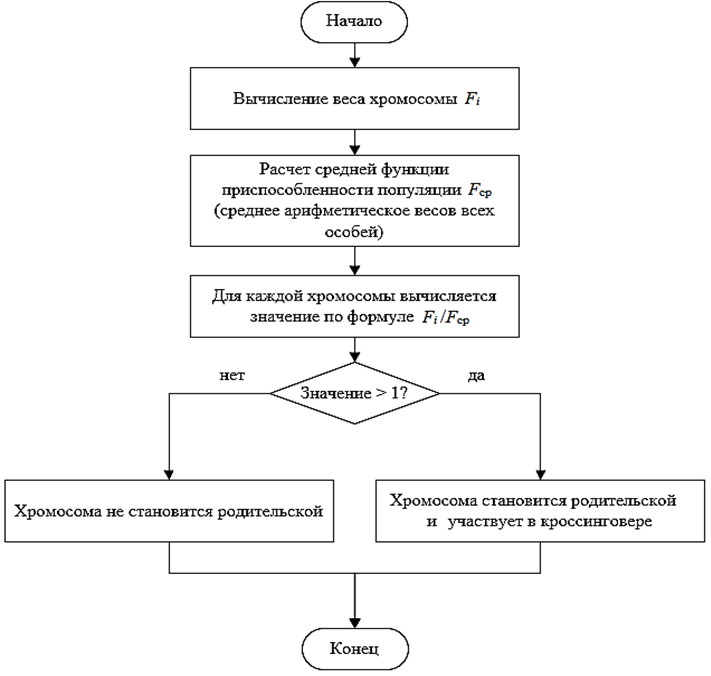
Блок-схема пропорционального отбора
Block diagram of proportional selection
Сначала вычисляется вес каждой хромосомы Fi, затем находят среднюю функцию приспособленности популяции Fср как среднее арифметическое значений весов всех особей, далее для каждой хромосомы вычисляется значение отношения ![]() . Если значение отношения больше 1, хромосома считается хорошо приспособленной и данное решение может стать родительским. Данный метод основан на классической теореме схем или теореме шаблонов, являющейся основной в теории генетических алгоритмов и дающей обоснование их эффективности. Цель данного этапа состоит
. Если значение отношения больше 1, хромосома считается хорошо приспособленной и данное решение может стать родительским. Данный метод основан на классической теореме схем или теореме шаблонов, являющейся основной в теории генетических алгоритмов и дающей обоснование их эффективности. Цель данного этапа состоит
в сохранении высокого качества решений при поддержании разнообразия. 6. Скрещивание (кроссинговер) – объединение частей двух родительских решений для создания потомства, что имитирует биологическое размножение и вносит разнообразие в популяцию.
Рассмотрим использование двухточечного кроссинговера, т. е. «обмен» данными в двух точках:

Потомство наследует характеристики от обоих родителей, что потенциально приводит к наилучшим решениям при решении задач в рамках работы над проектом.
7. Мутация – внесение случайных изменений в потомство для поддержания разнообразия и поиска новых решений, что предотвращает быструю конвергенцию, т. е. приход к единому решению при любых исходных данных. Пример мутации на основе полученного потомства:

Мутация гарантирует использование более широкого спектра решений, что позволит использовать все возможные варианты для работы сотрудников.
Целью использования генетических алгоритмов служит максимизация производительности и обеспечение распределения рабочей нагрузки с учетом наиболее сильных сторон каждого из сотрудников, а также степени удовлетворенности после выполнения задач того или иного типа.
Использование генетического алгоритма в планировании рабочих задач сотрудников экономического отдела
Генетический алгоритм возможно использовать для автоматизированного распределения задач среди сотрудников экономического отдела, учитывая их квалификацию, текущую загрузку и сроки выполнения работ [9]. Методика включает в себя следующие ключевые этапы:
1. Определение задачи и сбор актуальных данных. Разработка профилей сотрудников с указанием информации о работнике:
1.1 Навыков, например оценка эффективности затрат, разработка KPI и мониторинга их выполнения, умение работать с экономическими показателями и индикаторами.
1.2 Опыта, например работа с бюджетированием и планированием финансовых показателей, работа с налоговой декларацией, оптимизация затрат.
1.3 Рабочей нагрузки, т. е. занятости сотрудника с учетом уже запланированных встреч и выполняемых задач. В оценке учитывается сложность, сроки выполнения и связи с другими задачами в рамках данного и смежных проектов, а также исторические данные: прошлые задания, время выполнения и показатели производительности.
2. Представление хромосомы. Для начала алгоритм создает отдельные назначения задач, т. е. гены, после чего формирует хромосому на основании данных, полученных ранее. Ген возможно представить в виде кортежа
где I – идентификатор задачи, E – идентификатор сотрудника, W ∈ (0, 1) – весовой коэффициент соответствия, S ∈ [0, 1] – нечеткий показатель успешности, рассчитываемый на основе всех предыдущих результатов с учетом их давности, за нейтральное значение принимается 0,5, P ∈ (1, 5) – приоритет выполнения [10].
Хромосома должна соответствовать некоторым ограничениям, т. е. каждая задача поручается только одному сотруднику, сотрудники не перегружаются сверх своих возможностей и рабочего времени; задачи, требующие определенных навыков, распределяются среди сотрудников, которые ими обладают. 3. Генерация начальной популяции: алгоритм начинается с создания популяции случайно сгенерированных хромосом, каждая из которых представляет собой потенциальный план решения блока задач, при этом удовлетворяет ограничениям.
4. Создание функции пригодности: для планирования рабочих задач функция может учитывать следующее:
4.1 Время выполнения задачи, т. е. минимизацию общего времени, необходимого для выполнения всех задач в рамках проекта.
4.2 Баланс рабочей нагрузки за счет задействования сотрудников в полной мере, при этом избегая перегруза.
4.3 Соответствие квалификации, а именно назначение задач сотрудникам с наиболее подходящими навыками.
Функция приспособленности присваивает каждой хромосоме вес, т. е. пригодность сгенерированной хромосомы за счет анализа выполненной работы всего блока задач.
5. В процессе отбора выявляются наиболее эффективные хромосомы (варианты распределения задач), которые становятся родительскими для следующего поколения [11]. В экономическом отделе каждая хромосома может кодировать, например, распределение проектов между сотрудниками с учетом специализации и загрузки.
Допустим, отдел из 5 сотрудников обрабатывает 10 задач (I1–I10) разной сложности. Каждая задача имеет оценочное время выполнения и требуемую компетенцию, а каждый сотрудник – уровень загруженности и специализацию (навыки). Для расчета оценочной функции (Fi) необходимо определить следующие компоненты:
1. Скорость выполнения (F1) – рассчитывается как максимальное время среди сотрудников: если у сотрудника A задачи занимают 4 дня, В – 3 дня,C – 5 дней, то F1 = 5.
2. Равномерность загрузки (F2) – оценивается стандартное отклонение загрузки сотрудников по формуле
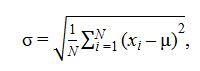
где N – количество сотрудников; xi – занятость i-го сотрудника, %; μ – средняя загруженность по отделу.
Допустим, загрузка А = 90 %, В = 70 %, С = 85 %, D = 60 %, Е = 75 %. Среднее – 76 %, соответственно, стандартное отклонение 11 %. Чем меньше σ, тем равномернее распределение задач.
3. Соблюдение компетенций (F3) – процент задач, назначенных сотрудникам с подходящими компетенциями, например, если 8 из 10 задач соответствуют навыкам исполнителей F3 = 80 %.
Далее необходимо произвести нормализацию и взвешивание, т. е. нормализовать каждую метрику, например привести к шкале от 0 до 1, а также назначить веса, зависящие от приоритетов отдела, допустим, скорость – 0,5, равномерность – 0,3, навыки – 0,2. При указанных значениях F1 = 0,7, F2 = 0,8 и F3 = 0,8. Итоговая Fi = 0,5 · 0,7 + 0,3 · 0,8 + + 0,2 · 0,8 = 0,75. Если Fср популяции равна 0,6, то
Fi / Fср = 0,75 / 0,6 ≈ 1,25 (>1), из чего следует, что хромосома перспективна.
6. Кроссинговер позволяет комбинировать успешные стратегии распределения задач. В экономических отделах это может обозначать объединение фрагментов рабочих графиков из разных родительских решений. Например, одноточечный кроссинговер может выглядеть следующим образом:

Перед внедрением потомка важно оценивать эффективность, например, возможны ли конфликты компетенций или превышение лимита рабочего времени.
7. Мутация помогает предотвратить «застревание» алгоритма в локальных оптимумах за счет случайного обмена задачами между сотрудниками или переназначения задач в рамках проектной работы, что поддержит генетическое разнообразие и позволит продолжить поиск наиболее оптимальных решений. Например, задача переносится от сотрудника А к сотруднику В, даже если изначально данное распределение не было оптимальным, или полностью снимается с перегруженного сотрудника и распределяется между остальными.
8. Итерация и конвергенция: процесс селекции, скрещивания и мутации необходимо повторять в течение нескольких поколений. Спустя время популяция эволюционирует, что позволит генерировать лучшие решения. Работа завершается, когда вес функции пригодности стабилизируется.
9. Адаптация в режиме реального времени. Генетический алгоритм предназначен для адаптации к изменяющимся условиям, например, если сотрудник становится недоступен, алгоритм может быстро переназначить его задачи, при этом с учетом особенностей генерации хромосомы, а также внедрить новые задачи в существующее решение. Для корректной адаптации алгоритма необходимо регулярное обновление данных о доступности сотрудников, загруженности, а также актуальных задачах, для обеспечения корректного распределения работ. Без своевременной актуализации информации алгоритм будет выдавать неоптимальные или устаревшие решения, что приведет к некорректной работе сотрудников отдела.
Важно подчеркнуть, что, несмотря на возможность автоматизированного распределения задач, окончательное решение должно оставаться за руководителем. Автоматически сгенерированный вариант может требовать корректировок, поскольку алгоритм опирается на формализованные параметры и не всегда способен учесть некоторые нюансы рабочей обстановки. Например, такие факторы, как межличностные отношения в отделе, временные личные обстоятельства сотрудников или иные аспекты, часто упускаются алгоритмом. Оптимальный принцип организации рабочих процессов предполагает симбиоз автоматизированного планирования и экспертной оценки руководителя, который при необходимости вносит коррективы с учетом всей полноты контекста.
Использование генетических алгоритмов содержит ряд преимуществ в разработке приложения. Во-первых, генетические алгоритмы используют широкий спектр решений, повышая вероятность нахождения глобального оптимума, т. е. глобально оптимизируя процесс. Во-вторых, гибкость, а именно возможность алгоритма подстраиваться под сложные ограничения, и учитывая множество задач. В-третьих, адаптивность, которая заключается в возможности алгоритма быстро перестраивать решения при изменении в доступности сотрудников, приоритетах задач и глобальных целях рабочего процесса.
Также данный алгоритм масштабируемый, т. е. подходит для организаций любого размера, от начинающего стартапа до корпораций с множеством рабочих проектов и задач.
Заключение
Внедрение генетического алгоритма при разработке приложения для планирования задач предлагает эффективное решение проблем, связанных с назначением задач вручную. Автоматизируя процесс и оптимизируя распределение задач, приложение может значительно повысить производительность сотрудников проектной команды, обеспечить справедливое распределение рабочей нагрузки на основании удовлетворенности предшествующим опытом, навыками и занятостью.
1. Хайрулина Л. Р., Ковалев А. И., Иваненко О. Б. Управление персоналом организации: учеб. пособие. Омск: Издат. центр КАН, 2021. 370 с.
2. Батраков М. В., Минханов Р. Ф. SCRUM как методология Agile разработки // Современные тенденции развития науки и технологий. 2017. № 2-3. С. 9–12.
3. Дружинина В. Д. Основные принципы методоло-гии SCRUM для управления проектами // Экономика. Социология. Право. 2022. № 3 (27). С. 17–21. DOI:https://doi.org/10.22281/2542-1697-2022-01-03-17-21.
4. Бурмистров П. Р. Исследование применения функционала системы "Jira" при управлении проектами // Евразийское научное объединение. 2021. № 3-3 (73). С. 188–190.
5. Никифоров Д. Л. Генетический алгоритм и область его применения // Решетневские чтения: материалы XXVI Междунар. науч.-практ. конф., посвящ. памяти генер. конструктора ракетно-косм. систем акад. М. Ф. Решетнева (Красноярск, 09–11 ноября 2022 г.): в 2 ч. Красноярск: Изд-во Сиб. гос. ун-та науки и технологий им. акад. М. Ф. Решетнева, 2022. Т. 2. С. 173–175.
6. Загинайло М. В., Фатхи В. А. Генетический алго-ритм как эффективный инструмент эволюционных алгоритмов // Инновации. Наука. Образование. 2020. № 22. С. 513–518.
7. Сергиенко А. Б., Галушин П. В., Бухтояров В. В., Сергиенко Р. Б., Сопов Е. А., Сопов С. А. Генетический алгоритм. Стандарт. Часть I. Описание стандартного генетического алгоритма (сГА) // Гитхаб. Harrix Проекты. Дата депон. 27.12.2010. № 61. 40 с. URL: item.asp?id=25044299 (дата обращения: 07.02.2025).
8. Шишкова Н. А. Генетический алгоритм как метод оптимизации // Проблемы науки. 2017. № 5 (18). URL: https://cyberleninka.ru/article/n/geneticheskiy-algoritm-kak-metod-optimizatsii (дата обращения: 08.02.2025).
9. Зотов А. В., Решетникова И. В. Использование генетических алгоритмов в задаче исследования функции // Будущее науки – 2020: сб. науч. ст. 8-й Междунар. молодеж. науч. конф. (Курск, 21–22 апреля 2020 г.): в 5 т. Курск: Изд-во Юго-Запад. гос. ун-та, 2020. Т. 3. С. 285–289.
10. Vijini M. Introduction to Genetic Algorithms. 2017. URL: https://vijinimallawaarachchi.com/2017/06/02/introduction-to-genetic-algorithms/ (дата обращения: 07.02.2025).
11. Кучумов А. В., Благовещенский И. Г., Благове-щенский В. Г., Зуева Ю. В., Лаптев И. К. Использование генетических алгоритмов для решения оптимизационных задач при производстве продукции // Роговские чтения: сб. докл. Науч.-практ. конф. с междунар. участием (Москва, 16 декабря 2022 г.). Курск: Университетская книга, 2023. С. 245–253.















