Russian Federation
Russian Federation
Russian Federation
The development of a Merkle post-quantum signature scheme based on a modified Lamport one-time signature algorithm is presented. The Merkle signature algorithm and the Lamport one-time signature algorithm are described. There is also a review of the current literature on the subject of the Merkle signature algorithm. A modified algorithm for Lamport's one-time electronic digital signature is described. The algorithms for key generation, signature generation, and verification of a previously generated signature are described in detail. The paper presents a software implementation of an electronic digital signature system with a graphical interface based on the developed algorithm, which allows key generation, signature generation and verification. A flowchart is provided for each of the main modules of the program, and the graphical interface of the developed software for each module is also demonstrated. The results of testing the modified algorithm are presented and its performance is compared with the standard algorithm. The test results confirm that using the modified algorithm allows faster verification of messages, while the speed of key generation and signature does not increase in comparison with the standard algorithm. The modified algorithm speeds up verification regardless of the message length. The results of the performed research are a modified Lamport one-time signature algorithm, which provides a higher signature verification rate compared to the classical algorithm, and a software tool with a graphical interface for generating and verifying a post-quantum electronic digital signature.
post quantum algorithm, electronic digital signature, Merkle signature, Lamport signatures
Введение
В современном мире алгоритмы электронной цифровой подписи играют все более и более важную роль в обеспечении информационной безопасности и противодействии киберпреступности. Электронная цифровая подпись (ЭЦП) играет важную роль в обеспечении безопасности коммуникаций и передачи электронных документов. Использование ЭЦП позволяет доказать отсутствие несанкционированных изменений документа, установить принадлежность подписи владельцу и обеспечивает неотказуемость от авторства подписи.
Развитие компьютерных технологий привело к появлению квантовых компьютеров, которые позволяют злоумышленникам осуществить взлом распространенных алгоритмов электронной подписи, основанных на алгоритмах RSA и Эль-Гамаля. По этой причине необходимо разрабатывать и внедрять алгоритмы ЭЦП, которые будут устойчивы к атакам с применением квантового алгоритма [1]. Одним из алгоритмов постквантовой электронной подписи является алгоритм подписи, основывающийся на построении дерева Меркла.
Объектом исследования является схема постквантовой ЭЦП Меркла на основе алгоритма одноразовой подписи Лампорта.
Предмет исследования – вычислительная сложность алгоритма подписи Меркла и его модификации
Цель исследования – разработка модифицированного алгоритма постквантовой подписи Меркла с использованием алгоритма одноразовой подписи Лампорта, который будет устойчив к современным квантовым атакам и для которого проверка подписи будет выполняться быстрее, чем при использовании классического алгоритма Лампорта.
В соответствии с целью исследования были определены следующие задачи:
– изучить актуальные публикации, связанные с исследованием алгоритма постквантовой подписи Меркла;
– разработать модификацию алгоритма одноразовой подписи Лампорта;
– выполнить программную реализацию классического алгоритма и модификации;
– реализовать программное средство для шифрования данных с использованием модифицированного алгоритма постквантовой подписи Меркла.
Основные методы исследования – анализ, сравнение и эксперимент.
Материалы и методы
Описание алгоритма подписи Меркла. Подпись Меркла – алгоритм многоразовой ЭЦП, который был опубликован в 1979 г. Ральфом Мерклом в техническом отчете «Secrecy, authentication, and public key systems» [2]. Алгоритм позволяет подписывать несколько сообщений одним открытым ключом, используя алгоритм одноразовой цифровой подписи. Основным преимуществом алгоритма является его устойчивость к атакам с использованием квантового компьютера. Это означает, что алгоритм Меркла может использоваться для построения схемы постквантовой ЭЦП.
Дерево Меркла – двоичное дерево, листья которого содержат значения хэша, а узлы дерева содержат хэш конкатенации двух значений дочерних вершин дерева [3]. Рассмотрим алгоритм построения дерева Меркла для схемы многоразовой ЭЦП:
1) cгенерировать N = 2k пар ключей (X, Y), где k – натуральное число, а каждая пара ключей представляет собой закрытый ключ X и открытый ключ Y схемы одноразовой цифровой подписи;
2) для каждого элемента Yj массива открытых ключей Y вычисляется значение HYj, где H – криптографическая хэш-функция. Каждое из этих значений обозначается как a0,j. Эти значения образуют нулевой слой дерева Меркла;
3) для каждого натурального числа i от 1 до k вычисляется j = 2k–i узлов дерева, которые обозначаются как ai, j и вычисляются по формуле
Значение ak, 0 является открытым ключом алгоритма подписи Меркла.
Алгоритм генерации подписи:
1. Выбрать пару ключей (X, Y), которая ранее не использовалась для генерации подписи.
2. Сгенерировать одноразовую подпись S', используя выбранную на предыдущем шаге пару ключей.
3. Вычислить аутентификационный путь, который необходим для верификации сгенерированной подписи. Аутентификационный путь состоит из k узлов сгенерированного дерева Меркла. Эти узлы выбираются таким образом, чтобы при наличии только лишь выбранного значения a0,i и аутентификационного пути было возможно вычислить значение ak,0. Для каждого целого n от 0 до k – 1 значение, которое является частью аутентификационного пути, определяется как
где xn, yn для выбранного a0,i определяются рекуррентными формулами
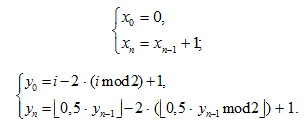
Цифровая электронная подпись sig, сгенерированная с использованием алгоритмов Меркла, имеет вид
Алгоритм верификации:
– верифицировать одноразовую подпись S'. Если верификация одноразовой подписи не была пройдена, то верификация подписи S также не пройдена. Если верификация S' выполнена успешно, то перейти к следующему шагу (вычисление A0);
– вычислить 
;
– для каждого натурального числа j от 1 до k вычислить
– сравнить значение Ak с pub. Если Ak = pub, то верификация пройдена успешно. Если Ak и pub не равны, то верификация не пройдена.
Описание алгоритма одноразовой подписи Лампорта. Подпись Лампорта – схема цифровой подписи с открытым ключом, которая была предложена Лампортом в 1979 г. [4]. Этот алгоритм представляет собой схему одноразовой цифровой подписи. Это означает, что одна пара ключей может быть использована для подписания только одного сообщения [5].
Схема подписи Лампорта состоит из алгоритмов генерации, подписания и верификации [6]. Результатом выполнения алгоритма генерации ключей является пара ключей (открытый ключ и закрытый ключ).
Алгоритм генерации ключей:
Шаг 1. Сгенерировать 256 пар случайных чисел длиной 256 бит, которые обозначаются как 
. Эти 512 чисел представляют собой закрытый ключ;
Шаг 2. Для каждого из 512 чисел, сгенерированных на шаге 1, вычислить Yi,j по формуле
512 значений, вычисленных на шаге 2, образуют открытый ключ.
Алгоритм генерации подписи:
Шаг 1. Выполнить хэширование сообщения.
Шаг 2. Для каждого бита bi, вычисленного на шаге 1 хэша, из соответствующей пары чисел закрытого ключа берется число 
Выбранное число обозначается как Ai. Выбранные 256 чисел составляют ЭЦП и отправляются вместе с сообщением. 256 чисел из секретного ключа, которые не были выбраны, должны быть удалены, чтобы избежать подделки подписи.
Алгоритм верификации для получателя сообщения:
Шаг 1. Вычислить хэш сообщения.
Шаг 2. Для каждого из чисел подписи A0, A1, …, A255 вычислить
Шаг 3. Для каждого бита 
вычисленного на шаге 1 хэша, сравнить 
Верификация пройдена успешно, если для всех i от 0 до 255 выполняется равенство
Если хотя бы для одного i равенство не выполняется, верификация считается непройденной.
Основным преимуществом алгоритма подписи Лампорта является высокая скорость подписания и верификации в сравнении с другими алгоритмами одноразовой подписи (например, подписью Винтерница). Недостатком алгоритма является большой размер открытого ключа и подписи [4].
Анализ релевантных работ
Одним из основных подходов к усовершенствованию алгоритмов постквантовой ЭЦП является модификация существующих алгоритмов одноразовой подписи. В статье [7] рассматривается применение алгоритма Лампорта в устройствах интернета вещей. Высокая производительность алгоритма позволила создать эффективную схему аутентификации при передаче данных между устройствами интернета вещей. В статье [8] авторы выполнили сравнение производительности алгоритма подписи Лампорта при использовании различных криптографических хэш-функций. Авторы сделали вывод, что увеличение длины хэша почти не влияет на скорость генерации подписи, но существенно замедляет генерацию ключа и верификацию подписи. В статье [9] разработана модификация алгоритма одноразовой подписи WOTS+. Эта модификация позволила ускорить генерацию ключа на 25 % и генерацию подписи на 16,7 %. Недостатком модификации является то, что верификация требует в 3,5 раза больше временив сравнении со стандартным алгоритмом. В статье [10] рассмотрены современные атаки на алгоритм WOTS+. В статье [11] применяется преобразование двоичных чисел в несмежную форму числа (non-adjacent form) для уменьшения количества выполняемых операций хэширования при генерации подписи. В работе [12] реализована модификация алгоритма WOTS+ с меньшим размером подписи в сравнении с классическим алгоритмом.
За последние пять лет было опубликовано несколько статей, в которых предложены новые постквантовые алгоритмы одноразовой ЭЦП. В работе [13] разработан алгоритм одноразовой постквантовой подписи с использованием доказуемо безопасных хэш-функций семейства SWIFFT, которые основываются на быстром преобразовании Фурье. В работе [14] предложен новый алгоритм одноразовой постквантовой подписи с использованием фильтра Блума. Фильтр Блума – структура данных, которая позволяет проверить наличие элемента в некотором множестве, но если элемента нет в множестве, то его отсутствие определяется лишь с некоторой вероятностью меньше 1.
Другим актуальным направлением исследований является оптимизация алгоритма подписи Меркла и его наиболее распространенной модификации – алгоритма XMSS. В работе [15] выполнена аппаратная реализация модифицированного алгоритма подписи Меркла XMSS с использованием алгоритма одноразовой подписи WOTS. В работе [16] представлена эффективная реализация XMSS для графического процессора. В работе [17] выполнена оптимизация алгоритма XMSS для процессоров, использующих систему команд RISC-V.
Модификация алгоритма подписи Лампорта
Алгоритм генерации ключей:
Шаг 1. Сгенерировать 512 случайных чисел длиной 256 бит каждое. Множество этих чисел должно быть разбито на 128 подмножеств, каждое из которых содержит по 4 числа. Числа в подмножестве с индексом i обозначаются как 
. Полученные числа представляют собой закрытый ключ.
Шаг 2. Для каждого из 512 чисел, сгенерированных на шаге 1, вычислить Yi,j по формуле
512 значений, вычисленных на шаге 2, образуют открытый ключ.
Алгоритм генерации подписи:
Шаг 1. выполнить хэширование сообщения.
Шаг 2. полученный хэш разбивается на 128 пар бит 
Шаг 3. Для каждой пары бит pi берется число Ai,j, где индекс j определяется как представление пары бит в десятичной системе счисления (например, если p = 11, то j = 3). Выбранное число обозначается Ai. 128 чисел Ai для i от 0 до 127 вместе составляют ЭЦП и отправляются вместе с сообщением. Остальные 384 числа из секретного ключа, которые не были выбраны, должны быть удалены, чтобы избежать подделки подписи.
Алгоритм верификации.
Получатель сообщения должен выполнить следующие действия:
– вычислить хэш сообщения;
– для каждого из чисел Ai вычислить Y'i по формуле
– разбить вычисленный хэш на 128 пар бит 
– для каждой из 128 пар бит p'i сравнить Y'i и Yi,j, где соответствующий каждому i индекс j определяется как представление пары бит p'i в десятичной системе счисления (аналогично шагу 3 генерации подписи). Верификация пройдена успешно, если для всех i от 0 до 127 выполняется равенство
Если хотя бы для одного i равенство не выполняется, верификация не пройдена.
Для уменьшения длины закрытого ключа в модификации используется криптографически стойкий генератор псевдослучайных чисел (КСГПСЧ) – алгоритм, позволяющий генерировать последовательность чисел, которые подчиняются заданному распределению и имеют статистические свойства, близкие к последовательности случайных чисел [18].
Использование КСГПСЧ позволяет значительно уменьшить объем памяти, который требуется для хранения закрытого ключа. Вместо закрытого ключа достаточно хранить лишь одно случайное число r длиной 256 бит. При необходимости выполнить подписание сообщения закрытый ключ генерируется с использованием КСГПСЧ, в который при инициализации на вход подается число r.
Доказательство криптостойкости модифицированного алгоритма.
Теорема 1. Если криптографическая хэш-функция H устойчива к атаке нахождения первого прообраза, то решение уравнения H(X||Y) = A для заданного A и неизвестных X и Y является неосуществимым на практике.
Доказательство. Предположим, что существует алгоритм для быстрого нахождения X и Y. В этом случае этот алгоритм может быть использован для решения уравнения H(X) = M (для этого достаточно выбрать произвольную строку, выполнить замену переменной X = X'||Y'), что противоречит утверждению об устойчивости функции H к атаке нахождения первого прообраза.
Теорема 2. Если криптографическая хэш-функция H устойчива к атаке нахождения первого прообраза, то решение уравнения H(A||X) = B для заданных A и B и неизвестного X является неосуществимым на практике.
Доказательство. Предположим, что существует алгоритм для быстрого нахождения X. В этом случае этот алгоритм может быть использован для решения уравнения H(X) = M (для этого достаточно выбрать произвольную строку A' и выполнить замену переменной X = A'||X'), что противоречит утверждению об устойчивости функции H к атаке нахождения первого прообраза.
Теорема 3. Если криптографическая хэш-функция H устойчива к атаке нахождения первого прообраза, то решение уравнения H(X||A) = B для заданных A и B и неизвестного X является неосуществимым на практике.
Доказательство аналогично доказательству теоремы 2, но при решении уравнения H(X) = M выполняется замена переменной X = X'||A'.
Используя теоремы 1–3, докажем криптостойкость модифицированного алгоритма ЭЦП Лэмпорта.
Пусть злоумышленник сгенерировал некоторое сообщение M. Чтобы сгенерировать подпись, которая пройдет верификацию с использованием опубликованного открытого ключа Y, злоумышленнику требуется выполнить хэширование сообщения M, разбить хэш на 128 пар бит p0, p1, …, p127 и для каждой пары бит pi найти два числа Bi и Ci, для которых выполняется равенство
(1)
где индекс j определяется представлением пары бит pi в десятичной системе счисления.
По теореме 1 эта задача является неосуществимой на практике для хэш-функции H, устойчивой к атаке нахождения первого прообраза.
Пусть злоумышленник пытается заменить сообщение M, для которого сгенерирована ЭЦП, на некоторое сообщение M'. Чтобы ранее сгенерированная подпись успешно прошла верификацию, злоумышленнику требуется сравнить пары бит p0, p1, …, p127 в разбиении хэша сообщения M с соответствующими парами бит p'0, p'1, …, p'127 в разбиении хэша сообщения M' и для каждого i, для которого pi ≠ p'i, найти два числа Bi и Ci, для которых выполняется равенство (1), что, как доказано ранее, неосуществимо на практике. Злоумышленник также может использовать в качестве Bi известное из подписи число Xi или использовать в качестве Ci число Ai. В первом случае злоумышленнику потребуется решить уравнение 
, что неосуществимо на практике по теореме 2, а во втором случае – решить уравнение 
, что неосуществимо на практике по теореме 3. Это означает, что модификация алгоритма подписи Лэмпорта устойчива к атакам при использовании криптографической хэш-функции, которая устойчива к атакам нахождения первого и второго прообраза.
Программная реализация
На основе разработанной модификации алгоритма подписи Меркла реализована система постквантовой электронной подписи, которая позволяет пользователю выполнять генерацию деревьев Меркла, подписывать файлы и осуществлять проверку подписи.
Программная реализация выполнена на языке Python 3.10.10. Графический интерфейс программного средства реализован с использованием библиотеки PyQt 6. В качестве криптографической хэш-функции пользователь может выбрать один из трех алгоритмов – SHA256, SHA3-256 и ГОСТ 34.11-2018 (для алгоритма ГОСТ 34.11-2018 используется версия с длиной хэша 256 бит). В качестве криптографически стойкого генератора псевдослучайных чисел используется функция urandom, которая является частью стандартной библиотеки os языка Python.
Программа состоит из трех модулей: модуля генерации дерева Меркла, который позволяет сгенерировать дерево Меркла для дальнейшего использования полученных ключей для генерации подписи; модуля подписания файлов, который обеспечивает подписание файлов с использованием одноразовых ключей подписи Лампорта, и модуля проверки подписи, который позволяет выполнить проверку подписи для ранее подписанных файлов, используя открытый ключ соответствующего дерева Меркла.
На рис. 1 показана блок-схема модуля генерации дерева Меркла.
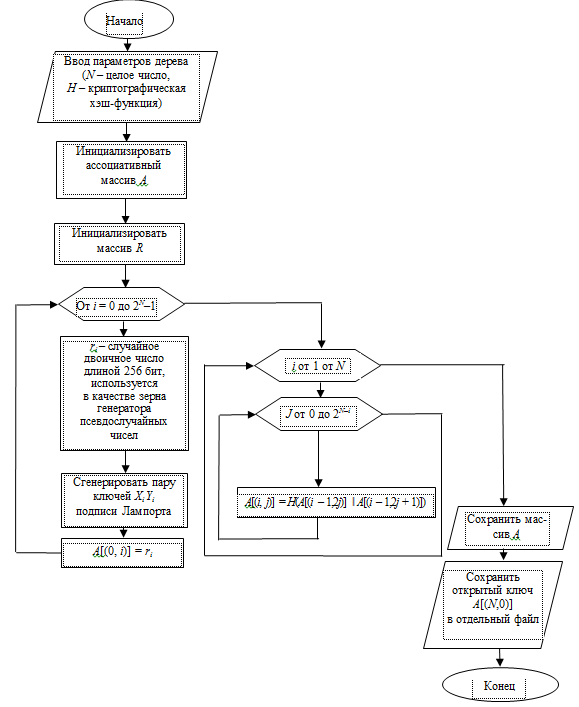
Рис. 1. Блок-схема модуля генерации дерева Меркла
Fig. 1. Block diagram of the Merkle tree generation module
В качестве параметров при генерации пользователем указываются параметр N, определяющий количество сообщений, которое можно подписать
с использованием открытого ключа дерева, и используемый алгоритм хэширования. Открытый ключ сохраняется в отдельный файл.
На рис. 2 показана блок-схема модуля генерации ЭЦП: для каждого из выбранных файлов генерируется подпись, которая сохраняется в отдельный файл.
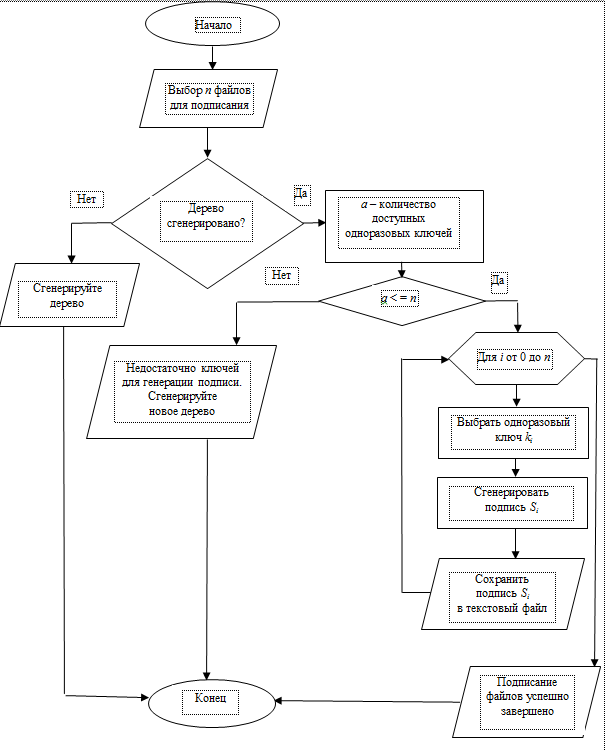
Рис. 2. Блок-схема модуля генерации подписи
Fig. 2. Flowchart of the signature generation module
На рис. 3 показана схема модуля проверки подписи. Для выполнения проверки требуется загрузить ранее подписанные файлы и файл с открытым ключом.
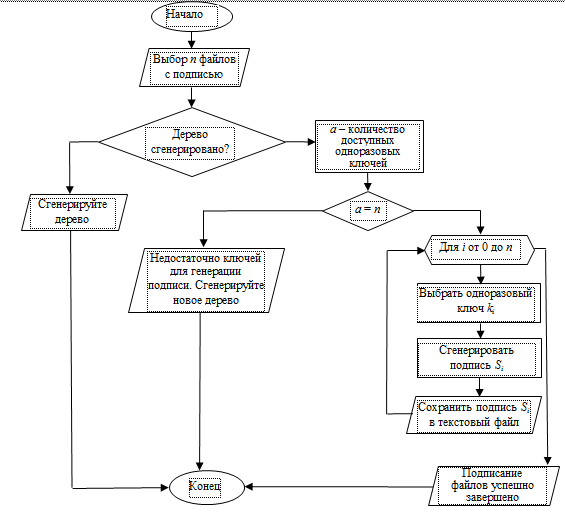
Рис. 3. Блок-схема модуля проверки подписи
Fig. 3. Flowchart of the signature verification module
На рис. 4 показано главное меню разработанного программного средства. Каждый из трех пунктов главного меню соответствует ранее описанным модулям системы генерации ЭЦП.
Рис. 4. Главное меню программного средства
Fig. 4. Main menu of the program
На рис. 5 показан пример успешной генерации дерева Меркла. На экране представлена информация обо всех ранее сгенерированных деревьях, выбранных параметрах и количестве доступных ключей для каждого дерева.
Рис. 5. Пример генерации дерева Меркла
Fig. 5. Example of Merkle Tree generation
На рис. 6 показан пример успешной генерации подписи для пяти выбранных пользователем файлов. На экран выводится информация обо всех выбранных для подписания файлах и соответствующих им файлах с подписью.
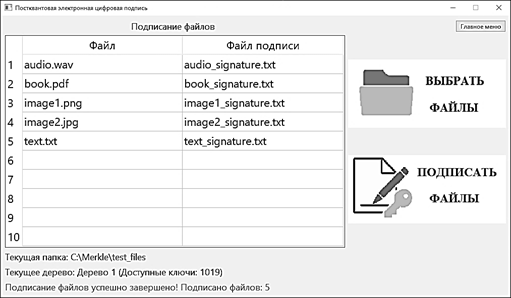
Рис. 6. Пример генерации подписи
Fig. 6. Example of signature generation
На рис. 7 показан пример успешной проверки подписи для пяти ранее подписанных файлов. На экран выводится информация о выбранных файлах, соответствующих им файлах подписи и результате проверки подписи.
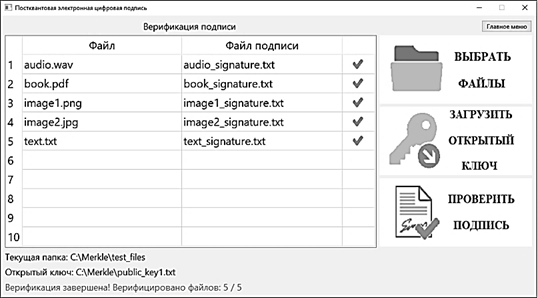
Рис. 7. Пример проверки подписи
Fig. 7. Example of signature verification
Тестирование модифицированного алгоритма
Для сравнения производительности стандартного алгоритма с разработанной модификацией проведен тест, который состоял из вызова функций генерации ключей, подписания и верификации подписи 1 000 000 раз для каждой из двух реализаций алгоритма подписи Меркла. В качестве криптографической хэш-функции использовался алгоритм SHA256, а в качестве криптографически стойкого генератора псевдослучайных чисел – функция os.urandom. Размер каждого сообщения – 8 КБ. Результаты тестирования представлены в табл. 1.
Таблица 1
Table 1
Результаты тестирования алгоритма
Algorithm testing results
|
Часть алгоритма |
Время выполнения для стандартного алгоритма, с |
Время выполнения для |
Результат |
|
Генерация ключей |
1,7924 |
1,7665 |
Модификация |
|
Подписание |
0,0439 |
0,0434 |
Модификация |
|
Верификация |
0,5396 |
0,2978 |
Модификация |
Было выполнено тестирование с целью сравнения времени выполнения верификации для сообщений различной длины при использовании стандартного и модифицированного алгоритмов. Для каждого возможного n = 16 · k, где k – целое число от 16 до 1 024, выполнена верификация 10 000 ранее подписанных сообщений размером n КБ стандартным и модифицированным алгоритмом. Далее для каждого n вычислено среднее время проверки подписи при применении стандартного и модифицированного алгоритма. По результатам тестирования построены графики, представленные на рис. 8.
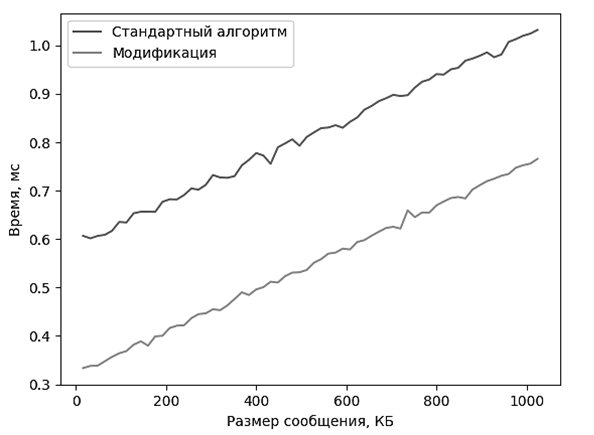
Рис. 8. Сравнение времени выполнения проверки подписи
для стандартного и модифицированного алгоритмов
Fig. 8. Perfomance comparison of signature verification between standard and modified algorithm
Тестирование алгоритма выполнено на компьютере с процессором Intel Core i5-2500K CPU 3.3 GHz.
В табл. 2 представлены результаты тестирования стандартного и модифицированного алгоритмов проверки ЭЦП для сообщений различного размера.
Таблица 2
Table 2
Результаты тестирования проверки подписи для сообщений различного размера
Test results of signature verification for messages of various sizes
|
Размер сообщения, КБ |
Среднее время |
Среднее время |
Разница между средним временем проверки |
|
16 |
0,6065 |
0,3335 |
0,273 |
|
32 |
0,6014 |
0,3379 |
0,2635 |
|
64 |
0,6087 |
0,3475 |
0,2612 |
|
128 |
0,6532 |
0,3818 |
0,2714 |
|
256 |
0,7045 |
0,4366 |
0,2679 |
|
512 |
0,8109 |
0,5361 |
0,2748 |
|
1 024 |
1,032 |
0,7656 |
0,2664 |
На основании выполненных тестов сделаны следующие выводы:
– использование модифицированного алгоритма позволяет ускорить выполнение проверки подписи;
– разница во времени выполнения проверки подписи между двумя алгоритмами не зависит от длины сообщения.
Обсуждение результатов
Результатами работы являются разработанная модификация алгоритма постквантовой подписи Меркла с использованием алгоритма одноразовой подписи Лампорта и реализованная на ее основе система ЭЦП с графическим интерфейсом. Преимуществом разработанной модификации является более высокая скорость выполнения проверки подписи. Тестирование показало, что разница между временем выполнения проверки подписи при использовании стандартного и модифицированного алгоритмов не зависит от длины сообщения (несмотря на то, что общее время проверки линейно зависит от длины сообщения из-за необходимости вычислять хэш сообщения). Из этого следует, что наиболее эффективно применять разработанную модификацию в приложениях, в которых требуется быстрая верификация подписи для большого количества сообщений небольшого (менее 1 МБ) размера.
Заключение
Основной результат, полученный в ходе исследования, – модификация алгоритма постквантовой подписи Меркла, которая в сравнении со стандартным алгоритмом обеспечивает более высокую производительность при проверке подписи. На основе разработанной модификации было реализовано программное средство для генерации и проверки электронной цифровой подписи. Выполнено тестирование производительности для двух версий алгоритма на сообщениях различной длины, которое подтвердило эффективность разработанной модификации.
1. Komarova A. V., Korobejnikov A. G. Analiz osnov-nyh sushchestvuyushchih postkvantovyh podhodov i skhem elektronnoj podpisi [Analysis of the main existing post-quantum approaches and electronic signature schemes]. Voprosy kiberbezopasnosti, 2019, no. 2 (30), pp. 58-68.
2. Chen Y. C., Chou Y.-P., Chou Y. C. An Image Au-thentication Scheme Using Merkle Tree Mechanisms. Future Internet, 2019, vol. 11 (7), p. 149. DOI: https://doi.org/10.3390/fi11070149.
3. Wang X., Lin W., Zhang W., Huang Y., Li Z., Liu Q., Yang X., Yao Y., Lv C. Integrating Merkle Trees with Transformer Networks for Secure Financial Computation. Applied Sciences, 2024, vol. 14 (4), p. 1386. DOI: https://doi.org/10.3390/app14041386.
4. Pankov K. N., Mironov Yu. B. Ispol'zovanie postkvantovyh algoritmov v zadachah zashchity informacii v telekommunikacionnyh sistemah [The use of post-quantum algorithms in information security tasks in telecommunication systems]. Moscow, Goryachaya liniya – Telekom Publ., 2023. 236 p.
5. Iavich M., Kuchukhidze T., Bocu R. A Post-Quantum Digital Signature Using Verkle Trees and Lattices. Symmetry, 2023, vol. 15 (12), p. 2165. DOI: https://doi.org/10.3390/sym15122165.
6. Josey T. B., Misbha D. S. Man-in-the-Middle Attack Mitigation in IoT Sensors with Hash Based Multidimensional Lamport Digital Signature. International Virtual Conference on Industry 4.0.IVCI 2021. Lecture Notes in Electrical Engineering. Singapore, Springer, 2023. Vol. 1003. Pp. 47-56. DOI: https://doi.org/10.1007/978-981-19-9989-5_5.
7. Abdullah G. M., Mehmood Q., Khan C. B. A. Adoption of Lamport signature scheme to implement digital signatures in IoT. International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), 2018, pp. 1-4. DOI: https://doi.org/10.1109/ICOMET.2018.8346359.
8. Zentai D. On the Efficiency of the Lamport Signature Scheme. Land Forces Academy Review, 2018, vol. 25 (3), pp. 275-280. DOI: https://doi.org/10.2478/raft-2020-0033.
9. Zhang K., Cui H., Yu Y. Revisiting the Constant-sum Winternitz One-time Signature with Applications to SPHINCS+ and XMSS. IACR Crypto2023, 2023, vol. 850, p. 29.
10. Kudinov M. A., Kiktenko E. O., Fedorov A. K. Security analysis of the W-OTS++ signature scheme: Updating security bounds. Matematicheskie voprosy kriptografii, 2021, vol. 12, iss. 2, pp. 129-145. DOI: https://doi.org/10.4213/mvk362.
11. Roh D., Jung S., Kwon D. Winternitz Signature Scheme Using Nonadjacent Forms. Security and Communication Networks, 2018, vol. 2018, pp. 1-12. DOI: https://doi.org/10.1155/2018/1452457.
12. Shahid F., Khan A., Malik S., Choo K. WOTS-S: A Quantum Secure Compact Signature Scheme for Distributed Ledger. Information Sciences, 2020, vol. 539, pp. 229-249. DOI: https://doi.org/10.1016/j.ins.2020.05.024.
13. Kalach K., Safavi-Naini R. An Efficient Post-Quantum One-Time Signature Scheme. Selected Areas in Cryptography – SAC 2015 Lecture Notes in Computer Science. Springer, Cham, 2015. Vol. 9566. Pp. 331-351. DOI: https://doi.org/10.1007/978-3-319-31301-6_20.
14. Shafieinejad M., Safavi-Naini R. A Post-Quantum One Time Signature Using Bloom Filter. 15th Annual Conference on Privacy, Security and Trust (PST). Calgary, 2017. Pp. 397-399. DOI: https://doi.org/10.1109/PST.2017.00056.
15. Cao Y., Wu Y., Wang W., Lu X. An efficient full hardware implementation of extended Merkle signature scheme. IEEE Transactions on Circuits and Systems, 2021, 12 p. DOI: https://doi.org/10.1109/TCSI.2021.3115786.
16. Wang Z., Dong X., Chen H., Kang Y. Efficient GPU Implementations of Post-Quantum Signature XMSS. IEEE Transactions on Parallel and Distributed Systems – 2023. 16 p. DOI: https://doi.org/10.1109/TPDS.2022.3233348.
17. Wang W., Jungk B., Walde J., Deng S. XMSS and Embedded Systems. Selected Areas in Cryptography – SAC 2019, Lecture Notes in Computer Science. Springer, Cham. 2019. Vol. 11959. Pp. 523-550. DOI: https://doi.org/10.1007/978-3-030-38471-5_21.
18. Nazarenko Yu. L. Kriptograficheskaya stojkost' generatorov sluchajnyh chisel. Algoritm Yarrou [Cryptographic strength of random number generators. The Yarrow algorithm]. European science, 2019, no. 10, pp. 24-29.
