Penza, Russian Federation
Russian Federation
Penza, Penza, Russian Federation
Estimating the entropy of long codes according to Shannon is a problem of exponential computational complexity as the length of the binary code sequence increases. At the same time, the sample size on which it is necessary to estimate the probabilities of the occurrence of rare events is rapidly growing. The purpose of the article is to simplify calculations by moving to logarithmic spaces of the probabilities of occurrence of rare events and the logarithm of the length of the analyzed code. It is showed that in the space of double logarithms for codes with dependent digits, linear extrapolation works well. This ultimately makes it possible to speed up the assessment of the entropy of long codes by eliminating the need to process large amounts of initial data using the Shannon formula. Using the classical Shannon formula, it is necessary to estimate the probability of the occurrence of certain code states, which leads to the complication of the task as the code length increases. You have to wait for rare events to appear. It is proposed to simplify the problem by symmetrizing the correlation matrix of the analyzed codes. The original asymmetric correlation matrix of arbitrary codes is replaced with an equivalent one, in which all correlation coefficients outside the diagonal are positive and identical. The coefficients of the symmetrized matrix are obtained by averaging the modules of the correlation coefficients of the original asymmetric matrix. Estimating correlation coefficients is a task that has quadratic computational complexity. That is, the entropy estimate using the proposed algorithm, instead of exponential computational complexity, has quadratic computational complexity. A nomogram is presented for the connection between the logarithm of the probability of errors of the second type (equivalent to Shannon entropy) and a long code sequence of correlation coupling coefficients of its digits r = {0.0, 0.2, 0.3, …, 0.8}. The algorithm is efficient on small samples of 16 to 32 examples of analyzed code sequences.
entropy estimation, Hamming entropy, Shannon entropy, small samples, symmetrization of correlations, asymmetric correlation matrix, symmetrized matrix
Введение
В середине прошлого века в теорию информации огромный вклад внес Клод Шеннон. Энтропия Шеннона сегодня рассматривается как классика в теории информации, в лингвистике, при анализе криптографических преобразований, а также во многих иных важнейших прикладных науках. Казалось бы, энтропии Шеннона вполне достаточно, и нет смысла создавать иные похожие математические конструкции. К сожалению, это оказалось не так, в ряде современных приложений, например при анализе стойкости к атакам подбора нейросетевых преобразователей биометрии человека в код его личного криптографического ключа [1], воспользоваться классическим методом вычисления энтропии технически невозможно.
Когда речь идет о стойких криптографических преобразованиях, такой проблемы не возникает. Все стойкие криптографические преобразования выполняются так, чтобы разряды кодов были независимыми (некоррелированными) и состояния разрядов кодов «0» и «1» были равновероятны. В этом случае энтропия Шеннона для каждого разряда единичная и складывается по всем разрядам.
Положение меняется, когда речь идет о вычислении энтропии текстов на русском или ином языке. В этом случае состояния разрядов для текста не являются равновероятными, кроме того, они оказываются зависимыми (коррелированными). Именно в этом случае теоретически можно воспользоваться методом оценки энтропии по Шеннону. При этом приходится сталкиваться с экспоненциальным ростом объема эталонных текстов для оценки вероятностей появления сочетаний знаков. В существующих справочниках заранее вычислены вероятности появления последовательностей, состоящих из
1–4 знаков. При этом оценку вероятностей можно повторить программно, опираясь на наличие текстов быстро увеличивающегося объема: 300 символов, 10 000 символов, 300 000 символов, 1 000 000 символов. Получить и хранить тексты такого объема технически вполне возможно на современных компьютерах. На обычном компьютере за приемлемое время можно рассчитать таблицы вероятности сочетаний знаков.
При попытках учета 32 знаков в 8-битной кодировке (ACSII кодировка текстов) задача оказывается технически не выполнима на обычном компьютере. Для оценок энтропии осмысленных паролей из
32 знаков (256 бит) [2] памяти обычного компьютера (до 100 Гбайт) для хранения требуемого размера текстов на русском языке уже недостаточно. В этом случае собрать эталонные тексты необходимого объема на русском языке и их обработать за приемлемое время технически невозможно. Причиной этого является экспоненциальная вычислительная сложность алгоритма Шеннона и экспоненциально растущие требования к объему выборки при оценке вероятностей появления в тексте того или иного сочетания рядом стоящих знаков.
Цель данной статьи – показать, что при определенных условиях экспоненциальная вычислительная сложность алгоритма Шеннона может быть уменьшена до квадратичной (до сложности вычисления коэффициентов корреляции). Для этого следует воспользоваться симметризацией корреляционных связей между зависимыми разрядами анализируемых кодовых последовательностей.
Проблема тестирования нейросетевых преобразователей биометрических данных в длинный код
Нейросетевой преобразователь биометрического образа человека в длинный код аутентификации, обученный автоматически алгоритмом ГОСТ Р 52633.5-2011 [3], после обучения должен быть протестирован. Быстрое тестирование выполняется алгоритмом ГОСТ Р 52633.3-2011 [4]. Этот стандарт решает проблему оценки энтропии за счет перехода от статистического анализа обычных длинных кодов к статистическому анализу амплитуд вероятности спектральных линий расстояний Хэмминга.
Если мы имеем нейросетевой преобразователь с длиной выходного кода аутентификации «Свой» в 256 бит и ожидаемой стойкостью к атакам подбора 105 попыток подстановки образов «Чужой», то при оценке вероятности ошибок второго рода P2 нам придется сформировать тестовую базу из 106 образов «Чужой». Предполагая объем памяти для хранения одного биометрического образа в 2 Кбайта, мы получим необходимый объем оперативной памяти для тестирования порядка 2 Гбайт.
Еще одним важным моментом является то, что нейросетевые операции преобразования биометрических данных желательно выполнять в доверенной вычислительной среде [5], например на процессоре SIM-карты, микро-SD карты, RFID-карты с ограниченными вычислительными возможностями. Тогда эмулирование одного отклика обученной нейросети потребует 0,3 секунды. В результате общее время тестирования может составить более трех суток.
Требования к объему памяти (к числу тестовых образов «Чужой»), а также требования к вычислительным возможностям процессора удается сократить, если при тестировании мы знаем код «Свой». Тогда мы имеем возможность перейти от статистического анализа обычных кодов к анализу статистик расстояний Хэмминга:
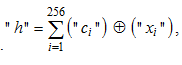 (1)
(1)
где "ci" – значение i-го разряда кода «Свой»; "xi" – значение i-го разряда кода «Чужой»; Å – операция сложения двух разрядов двух кодов по модулю два. Для обозначения целых чисел используются кавычки " ", все обозначения без кавычек – континуумы. Такой прием обычно используется в программировании, дискретные или строковые переменные (например, названия файлов) записываются в кавычках. Во всех иных случаях переменная считается непрерывной (континуальной).
В пространстве расстояний Хэмминга происходит экспоненциальное упрощение задачи, т. к. уже нет необходимости анализировать большое поле кодов «Чужой» с 2256 возможными состояниями. Вместо них мы получаем всего 257 возможных кодовых состояний расстояний Хэмминга между кодом «Свой» и всеми иными кодами «Чужой».
Процедура использования малой выборки образов «Чужой» для оценки вероятностей ошибок второго рода иллюстрируется рис. 1.
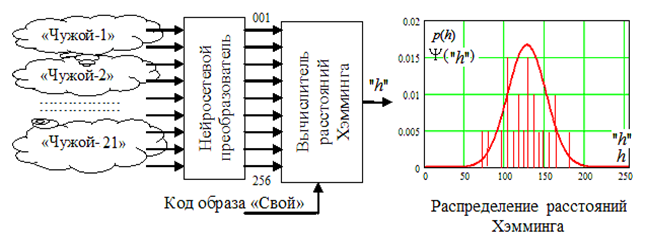
Рис. 1. Тестирование нейросетевого преобразователя в пространстве расстояний Хэмминга алгоритмом
ГОСТ Р 52633.3-2011 [2]
Fig. 1. Testing of a neural network converter in the Hamming distance space using the USS R 52633.3-2011 algorithm [2]
Следует отметить, что свертка Хэмминга 256 случайных пар состояний «0» и «1» – (1) является эффективным нормализующим преобразованием. В связи с этим дискретное нормальное распределение амплитуд вероятности Y("h") расстояний Хэмминга мы можем в первом приближении заменить непрерывным нормальным распределением – p(h), приравняв их математические ожидания E(Y("h")) » E(p("h")) и стандартные отклонения s(Y("h")) » s(p("h")).
В рамках гипотезы нормальности может быть легко вычислена вероятность ошибок второго рода (вероятность ошибочного принятия образа «Чужой» за образ «Свой»):
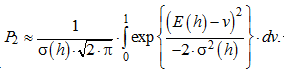 (2)
(2)
Если теперь перейти к двоичному логарифму выражения (2), мы получим оценку энтропии по шкале Хэмминга. Ее формальное введение в обширную практику анализа биометрических данных состоялось в 2011 г. Такой технический прием можно считать в биометрии узаконенным с момента ввода в действие стандарта ГОСТ Р 53633.3-2011 [4].
С одной стороны, прошедшие 10 лет практики подтвердили эффективность процедур вычисления энтропии по шкале Хэмминга [6–8], однако, с другой стороны, биометрико-криптографическая общественность, как и ранее, с настороженностью относится к энтропии, вычисленной по шкале Хэмминга. Причина этого проста: шкала энтропии Хэмминга и привычная всем классическая шкала энтропии Шеннона различаются.
Следуя рекомендациям ГОСТ Р 52633.3-2011 [4] удается снизить затраты на тестирование от 100 до 100 000 раз в зависимости от стойкости биометрической защиты. Однако столь значительные эффекты сокращения объема памяти и ускорения вычислений вызывают определенное недоверие среди экспертного сообщества из-за отсутствия глубоких исследований по связи шкалы энтропии Хэмминга и шкалы энтропии Шеннона. В более широком плане такая же проблема связана и с тем, как иные известные способы вычисления энтропии (иные шкалы энтропии) соотносятся с хорошо изученной и широко представленной в разнотипных методических указаниях шкалой энтропии Шеннона. Интуитивно понятна причина применения разных способов вычисления энтропии Раньи – Циллиса [9], энтропии алгоритмической сложности [10], эпсилон-энтропии Колмогорова [11], энтропии частоты слов Ципфа – Ман-дельброта [12]. Для той или иной частной задачи удобным оказывается вычисление энтропии своим способом, соответственно, нужны исследования, позволяющие в ближайшем будущем построить корректное приведение энтропии разных шкал к одной шкале (например, к шкале энтропии Шеннона как наиболее часто применимой на практике).
Упрощение вычисления энтропии по шкале Шеннона за счет симметризации корреляционных связей разрядов биометрических кодов
Следует отметить, что для кодов с независимыми состояниями разрядов вычисление энтропии является простой задачей для криптографии. В рамках гипотезы независимости вероятность появления двух одинаковых состояний «0» или «1» перемножается. Если вероятности появления состояний «0» и «1» в разных разрядах кода равновероятны, то вероятности появления состояний «0» в каждом разряде перемножаются, а энтропии Шеннона, вычисленные для каждого из 256 разрядов, складываются.
Очевидно, что для каждой из возможных комбинаций разрядов кодов мы можем вычислить матрицу корреляционных связей. Если размерность корреляционной матрицы велика, найти энтропию ее кодовых комбинаций сложно. Однако мы можем упростить задачу, предположив, что матрица корреляционных связей симметрична (все коэффициенты корреляции вне диагонали одинаковы). Для исходной n-мерной асимметричной корреляционной матрицы с совершенно разными и по знаку, и по модулю коэффициентами корреляции [13] необходимо найти эквивалентную симметризованную матрицу
с коэффициентами корреляции r̃, одинаковыми вне диагонали:
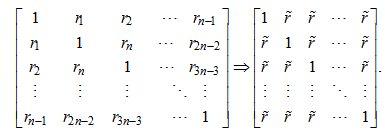
Коэффициенты корреляции эквивалентной симметризованной матрицы вычисляются суммированием модулей реальных коэффициентов корреляции асимметричной матрицы:
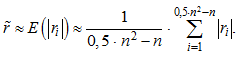 (3)
(3)
Для асимметричных корреляционных матриц малой размерности оценка (3) может давать значительные ошибки, однако уже при матрицах размерности 32 × 32 и более ошибка приближения становится вполне приемлемой для практики. При размерности асимметричной корреляционной матрицы 256 × 256 ошибкой приближения оценки (3) можно пренебречь.
Симметрия эквивалентной корреляционной матрицы удобна тем, что позволяет легко моделировать векторы данных с равной коррелированностью. Для этого достаточно умножить вектор независимых случайных данных на симметризованную связывающую матрицу:
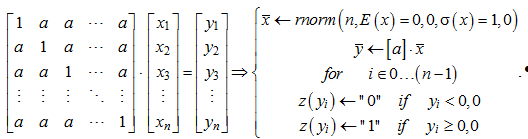
Умножать связывающую данные матрицу следует на вектор из n случайных чисел, полученных от программного генератора с нормальным распределением нулевым математическим ожиданием E(x) = 0,0 и единичным стандартным отклонением s(х) = 1,0. В этом случае положительные значения связанных данных z(yi) должны давать состояния «1», а отрицательные значения z(yi) должны соответствовать состоянию «0». Из-за того, что вычисление энтропии по Шеннону имеет экспоненциальную вычислительную сложность, обычные компьютеры не способны оценивать энтропию Шеннона для n = 20 бит и более. Для n более 20 для быстрых вычислений не хватает оперативной памяти, а хранение данных на жестком диске многократно тормозит моделирование. В связи с этим обстоятельством численный эксперимент, отображенный на рис. 2, выполнялся для кодов длиной в 20 бит и менее.
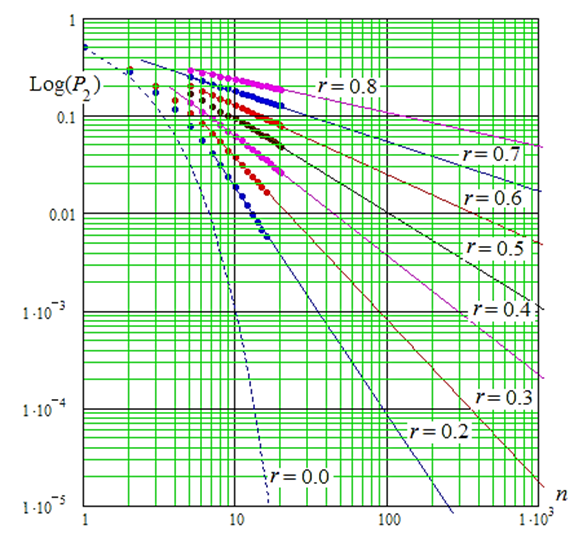
Рис. 2. Номограмма связывания логарифма вероятности ошибок второго рода
с логарифмом числа разрядов анализируемого кода
при разных значениях корреляционной связанности разрядов анализируемых кодов P2(n = 1) = 0,5
Fig. 2. Nomogram for connecting the logarithm of the probability of errors of the second type
with the logarithm of the number of bits of the analyzed code for different values
the correlation connectivity of the bits of the analyzed codes P2(n = 1) = 0.5
Из рис. 2 видно, что в логарифмических координатах связь энтропии Шеннона с числом разрядов анализируемых кодов хорошо описывается линейной аппроксимацией для длины кодов более 20 бит. Это позволяет нам создавать простые линейные таблицы для быстрых алгоритмов вычисления энтропии Шеннона длинных кодов с одинаково коррелированными разрядами. Например, такая таблица может быть построена на основе следующего линейного приближения:
![]() (4)
(4)
В таблице приведены различные соотношения коэффициентов линейной аппроксимации, соответствующие разным значениям корреляционной сцепленности исследуемых кодовых последовательностей.
Коэффициенты линейной аппроксимации данных
в координатах двух логарифмических осей (формула (4), рис. 2)
Coefficients of linear approximation of data
in coordinates of two logarithmic axes (formula (4), fig. 2)
|
r̃ |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
a0(r̃) |
5,0 |
2,0 |
1,3 |
0,7 |
0,6 |
0,52 |
0,5 |
0,5 |
0,5 |
|
a1(r̃) |
2,333 |
1,667 |
1,256 |
0,667 |
0,511 |
0,358 |
0,3 |
0,15 |
0,0 |
Заключение
Чтобы оценить энтропию Шеннона новым методом, достаточно вычислить коэффициенты взаимной корреляции между несколькими десятками случайно выбранных пар разрядов на малой выборке в 20 примеров кодов образов «Чужой». Далее следует усреднить модули полученных коэффициентов корреляции и воспользоваться таблицей для оценок по (4). В итоге получается снижение сложности вычислений, сопоставимое с процедурами ГОСТ Р 52633.3-2011 [4]. Получается, что рассматриваемая в данной статье линейная экстраполяции (4) дает примерно такой же выигрыш для энтропии Шеннона, что и нормальная экстраполяция (2) для энтропии Хэмминга. Более того, в работах [14–16] приведены условия, при которых в двойных логарифмических координатах при использовании бета-распределения удается добиться практически линейной связи данных для энтропии Хэмминга. Все это позволяет надеяться на то, что в ближайшее время удастся достаточно надежно связать шкалу энтропии Хэмминга и шкалу энтропии Шеннона.
1. GOST R 52633.0-2006. Zashchita informatsii. Tekhnika zashchity informatsii. Trebovaniia k sredstvam vysokonadezhnoi biometricheskoi autentifikatsii [Infor-mation protection. Information security techniques. Re-quirements for highly reliable biometric authentication tools]. Moscow, Standartinform Publ., 2006. 19 p.
2. Malygina E. A., Ivanov A. I., Iazov Iu. K., Nadeev D. N. Prognozirovanie znachenii entropii dlinnykh kodovykh posledovatel'nostei, porozhdaemykh estestvennymi i iskusstvennymi iazykami [Predicting the entropy values of long code sequences generated by natural and artificial languages]. Infokommunikatsionnye tekhnologii, 2014, vol. 12, no. 2, pp. 12-15.
3. GOST R 52633.5-2011. Zashchita informatsii. Tekhnika zashchity informatsii. Avtomaticheskoe obuchenie neirosetevykh preobrazovatelei biometriia-kod dostupa [Information protection. Information security techniques. Automatic training of neural network converters biometrics-access code]. Moscow, Standartinform Publ., 2012. 20 p.
4. GOST R 52633.3-2011. Zashchita informatsii. Tekhnika zashchity informatsii. Testirovanie stoikosti sredstv vysokonadezhnoi biometricheskoi zashchity k atakam podbora [Information protection. Information security techniques. Testing the resistance of highly reliable biometric protection tools to selection attacks]. Moscow, Standartinform Publ., 2012. 16 p.
5. Ivanov A. I., Iunin A. P. Embrion iskusstvennogo intellekta: kompaktnaia neirosetevaia proverka kachestva sluchainykh posledovatel'nostei, poluchennykh iz bio-metricheskikh dannykh: preprint [The embryo of artificial intelligence: compact neural network quality control of random sequences obtained from biometric data: preprint]. Penza, Izd-vo PGU, 2021. 68 p.
6. Volchikhin V. I., Ivanov A. I., Bannykh A. G. Reguliarizatsiia vychisleniia entropii vykhodnykh sostoianii neirosetevogo preobrazovatelia biometriia-kod, postroennaia na razmnozhenii maloi vyborki iskhodnykh dannykh [Regularization of the calculation of the entropy of the output states of the neural network converter biometrics-code, based on the reproduction of a small sample of source data]. Izvestiia vysshikh uchebnykh zavedenii. Povolzhskii region. Tekhnicheskie nauki, 2017, no. 4 (44), pp. 14-23.
7. Volchikhin V. I., Ivanov A. I. Neirosetevaia molekula: reshenie obratnoi zadachi biometrii cherez programmnuiu podderzhku kvantovoi superpozitsii na vykhodakh seti iskusstvennykh neironov [Neural network molecule: solving the inverse problem of biometrics through software support for quantum superposition at the outputs of a network of artificial neurons]. Vestnik Mordovskogo universiteta, 2017, vol. 27, no. 4, pp. 518-523. DOI:https://doi.org/10.15507/0236-2910.027.201704.518-529.
8. Ivanov A. I. Iskusstvennyi intellekt vysokogo dove-riia. Uskorenie vychislenii i ekonomiia pamiati pri testiro-vanii bol'shikh setei iskusstvennykh neironov na malykh vyborkakh [Artificial intelligence of high trust. Acceleration of calculations and memory savings when testing large networks of artificial neurons on small samples]. Sistemy bezopasnosti, 2020, no. 5, pp. 60-62.
9. Bashkirov A. G. Entropiya Ren'i kak statisticheskaya entropiya dlya slozhnyh sistem [Rényi entropy as statistical entropy for complex systems]. Teoreticheskaya i matematicheskaya fizika, 2006, vol. 149, no. 2, pp. 299-318.
10. Kolmogorov A. N. Tri podhoda k opredeleniyu po-nyatiya «kolichestvo informacii» [Three approaches to defining the concept of «amount of information»]. Problemy peredachi informacii, 1965, vol. 1, no. 1, pp. 3-11.
11. Ilyin A. A., Chepyzhov V. V. O kolmogorovskoj epsilon-entropii attraktorov avtonomnyh i neavtonomnyh dinamicheskih sistem [On Kolmogorov epsilon-entropy of global attractors for autonomous and non-autonomous dynamical systems]. Informacionnye processy, 2019, vol. 19, no. 3, pp. 339-353.
12. Sinitsyn V. Yu., Kashparova V. S. Chastotnye svojstva leksiki nauchnyh tekstov i zakony Cipfa vysshih poryadkov [Frequency properties of the lexis of scientific texts and Zipf's laws of higher orders]. Vestnik RGGU. Seriya: Informatika. Informacionnaya bezopasnost'. Matematika, 2022, no. 4, pp. 75-91. DOI:https://doi.org/10.28995/2686-679X-2022-4-75-91.
13. Ivanov A. I., Bannykh A. G., Serikova Iu. I. Uchet vliianiia korreliatsionnykh sviazei cherez ikh usrednenie po moduliu pri neirosetevom obobshchenii statisticheskikh kriteriev dlia malykh vyborok [Taking into account the influence of correlations through their modulo averaging with neural network generalization of statistical criteria for small samples]. Nadezhnost', 2020, vol. 20, no. 2, pp. 28-34.
14. Ivanov A. I., Lozhnikov P. S., Bannykh A. G. A Simple Nomogram for Fast Computing the Code Entropy for 256-Bit Codes That Artificial Neural Networks Output. Journal of Physics: Conference Series, 2019, vol. 1260, iss. 2. DOI:https://doi.org/10.1088/1742-6596/1260/2/022003.
15. Ivanov A. I., Bannykh A. G., Lozhnikov P. S., Sulavko A. E., Inivatov D. P. Possibility of Decrease in a Level of Data Correlation During Processing Small Sam-ples Using Neural Networks by Generating New Statistic Tests. Journal of Physics: Conference Series, 2020, vol. 1546. DOI:https://doi.org/10.1088/1742-6596/1546/1/012080.
16. Ivanov A. I., Bannykh A. G. Bystraia otsenka entropii dlinnykh kodov s zavisimymi razriadami na mikrokontrollerakh s malym potrebleniem i nizkoi razriadnost'iu (obzor literatury po snizheniiu razmernosti zadachi) [Fast estimation of the entropy of long codes with dependent bits on microcontrollers with low consumption and low bit depth (review of the literature on reducing the dimension of the problem)]. Inzhenernye tekhnologii i sistemy, 2020, vol. 30, no. 2, pp. 300-312. DOI:https://doi.org/10.15507/2658-4123.030.2020.02.300.312.















