Russian Federation
Russian Federation
The article considers the stratification of concomitant diagnoses of Covid-19 recovery statistics for the city of Irkutsk for 2020-2021. The previous study was conducted without taking into account such stratification. Various options for approximating real statistics by Gaussian and Lorentz functions, gamma distribution, and Johnson curves are considered. It is shown that the stratification of recovery statistics improves the approximation of Gaussian and Lorentz functions in comparison with integral statistics, and the construction of an approximation based on the Lorentz function always describes the real statistics better. Estimates of mathematical expectation and variance based on statistical data are consistent with estimates of these values based on the Gaussian approximation of statistics by the least squares method, i.e. the approaches are equivalent. At the same time, calculations of the Pearson Chi-squared criterion reject the hypothesis that empirical data correspond to the assumed theoretical distribution. Therefore, we cannot talk about finding the distribution function, but only about approximating statistics by certain types of curves. The fitting of empirical data by Gaussian and Lorentz functions was carried out using the least squares method. In general, the approximation error due to the stratification of statistics on concomitant diagnoses decreases from 6% to 3%.
coronavirus infection, concomitant diagnoses, fitting curves, approximation, Gaussian function, Lorentz function, gamma distribution, Johnson curve
Введение
В настоящее время продолжается исследование различных особенностей коронавирусной инфекции [1–9]. В работе рассмотрены статистические данные по выздоровлению пациентов в стационарных и амбулаторных условиях в г. Иркутске в 2020–2021 гг., предоставленные в обезличенном виде ГБУЗ «Иркутская областная клиническая больница» (ИОКБ). Эти данные уже использовались авторами в работе [2], где применялись методы математической статистики и математического моделирования. Была изучена функция распределения (плотность вероятности) выздоровления больных, представлена аппроксимация функции распределения гауссовой и лоренцевой функциями с тремя подгоночными параметрами, найденными методом наименьших квадратов. Оказалось, что лоренцева функция лучше аппроксимирует статистические данные, чем гауссова функция. Точность аппроксимации в максимуме распределения вероятностей получилась 6,9 и 5,1 % для гауссовой и лоренцевой аппроксимаций соответственно. Первоначально авторы предполагали, что статистика будет описываться нормальным распределением вероятностей, т. е. гауссовой функцией. Однако практические расчеты не согласуются с таким предположением. Расчет критерия Пирсона для наилучшей аппроксимации статистических данных не подтверждает гипотезу о нормальном распределении выздоровлений.
Знание функции распределения выздоровлений пациентов позволяет упростить решение различных статистических задач теории эпидемий, например, позволяет получить формулу для среднего времени лечения в стационарных и амбулаторных условиях, а также вычислить средние затраты на лечение одного больного.
Ниже покажем, что основной причиной отклонения выписки выздоровевших пациентов от нормального распределения является наличие расслоения больных на группы с различными сопутствующими диагнозами. Учет расслоения улучшает аппроксимацию статистических данных до 3 %.
Построение сводных таблиц и графиков
В процессе работы в ГБУЗ ИОКБ Н. Е. Васильевой (врач-хирург) и С. С. Козловой (ИТ-специалист) была создана условная группировка сопутствующих диагнозов и осложнений, которую больница использовала при проведении внутренней экспертизы летальных случаев. Этот механизм обработки данных был введен в медицинскую информационную систему «Ариадна», в которой работает ГБУЗ ИОКБ на данный момент. Согласно этой классификации все сопутствующие диагнозы можно условно разбить на группы заболеваний в зависимости от поражения конкретной системы органов (табл.).
Укрупненная группировка по сопутствующим заболеваниям
An enlarged grouping of concomitant diseases
|
Сопутствующий диагноз |
Медицинский классификатор |
Выписка |
Всего |
|
Заболевания системы кровообращения |
I00-I99 |
25 955 |
373 410 |
|
Злокачественные новообразования |
C00-C48 |
696 |
10 595 |
|
Заболевания органов желудочно-кишечного тракта |
K00-K93 |
6 133 |
89 932 |
Окончание табл.
Ending of the table
|
Сопутствующий диагноз |
Медицинский классификатор |
Выписка |
Всего |
|
Травмы, отравления |
S00-T98 |
200 |
3 003 |
|
Инфекционные болезни |
A00-B99 |
55 505 |
748 650 |
|
Заболевания органов дыхания |
J00-J99 |
60 285 |
812 650 |
|
Заболевания мочевыделительной системы |
N00-N99 |
4 558 |
67 346 |
|
Болезни обмена веществ |
E00-E90 |
14 236 |
203 520 |
|
Гнойные заболевания мягких тканей |
L00-99 |
94 |
1 327 |
|
Заболевания костно-мышечной системы |
M00-M99 |
47 |
631 |
|
Болезни крови, нарушения свертываемости, иммунодефициты |
D50-89 |
3 194 |
46 405 |
|
Заболевания нервной системы |
G00-99 |
7 |
79 |
|
Неблагоприятные эффекты |
W00-X59 Y40-84 |
15 |
147 |
|
Заболевания лор-органов |
Н65-Н75 |
43 |
407 |
|
Алкогольная болезнь |
ХАИ |
8 |
91 |
Для анализа каждая группировка рассмотрена отдельно, независимо от того, были ли пересечения. На основе данных, приведенных в таблице, строим график среднего времени выздоровления по каждой группе (рис. 1: ломаная линия – экспериментальные данные, гладкая сплошная – их аппроксимация параболой, выражение для которой приведено на поле графика).
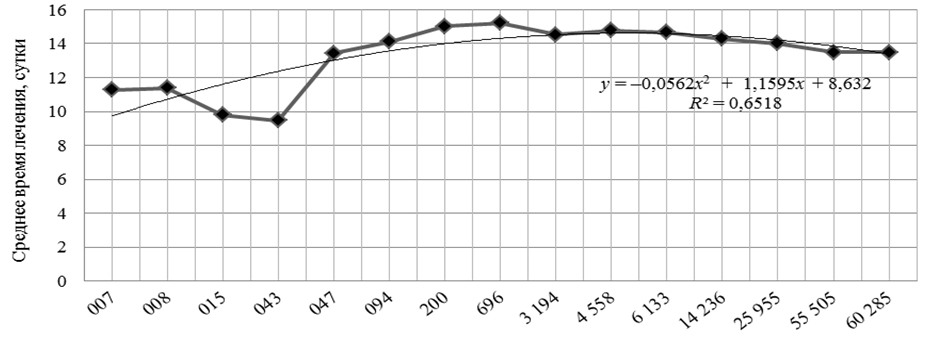
Рис. 1. Среднее время выздоровления по сопутствующим группам заболеваний
Fig. 1. Average recovery time for concomitant groups of diseases
В зависимости от сопутствующего диагноза среднее время лечения отмечается в диапазоне 9–15 дней.
Интегральная статистика выздоровлений
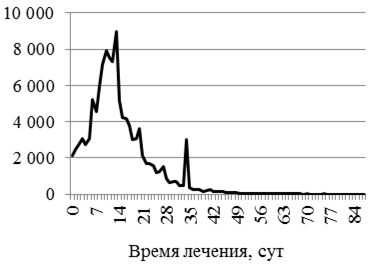
На рис. 2 представлена статистика выздоровлений пациентов по г. Иркутску за 2020–2021 гг. в зависимости от времени лечения. На рис. 2, а приведен график выздоровления пациентов при амбулаторном лечении, на рис. 2, б – при госпитализации. Локальные максимумы приходятся на 7, 14, 21, 28, 35 дни болезни и связаны с посещением врача
в поликлинике амбулаторными больными 1 раз в неделю. Это один из факторов, заметно ухудшающих статистику амбулаторного лечения.
а б
в г
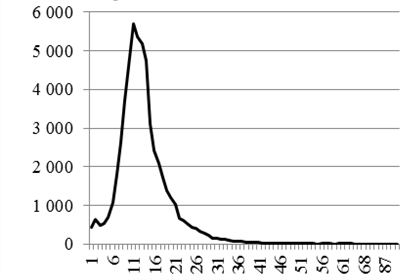
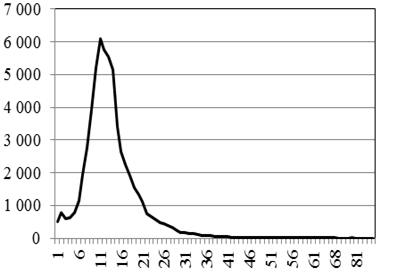
Рис. 2. Статистика выздоровлений по г. Иркутску за 2020–2021 гг.
при амбулаторном лечении (а), при госпитализации интегральной (б), A00-B99 (в), J00-J99 (г)
Fig. 2. Statistics of recoveries in the city of Irkutsk for 2020-2021
for outpatient treatment (a), for integral hospitalization (б), A00-B99 (в), J00-J99 (г)
Поиск аппроксимации для функции распределения
Рассмотрим выздоровление при госпитализации. Данные для обработки соответствуют рис. 2, б:
где ti – нумерация суток, ni – скорость выздоровления пациентов, т. е. количество пациентов, выздоровевших в течение суток ti,
где n – полное количество выздоровевших пациентов.
Математическое ожидание задачи, т. е. среднее время лечения одного пациента:
Дисперсия рассматриваемой выборки:
.
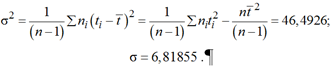Функция вероятности нормального распределения:
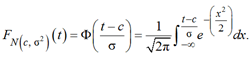
Константы определяются ниже.
Отсюда плотность вероятности:
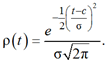
Максимум распределения достигается в точке
t = c. Величина c определяет сдвиг функции распределения по оси времени вправо при условии, что ось времени направлена слева направо.
Рассмотрим аппроксимацию статистики гауссовой и лоренцевой функциями. Для гауссовой функции
(1)
Согласование констант в (1) со статистическими моментами: 
. Для лоренцевой функции
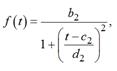
коэффициент b2 соответствует максимальному значению функции, c2 соответствует положению максимума функции на оси абсцисс, коэффициент d2 равен полуширине распределения на полувысоте.
В случае малости величины
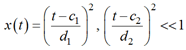
обе функции дают одинаковый вид разложений
Это означает, что обе аппроксимации родственны, за исключением далекого хвоста распределения. Гауссова аппроксимация спадает по экспоненте, а лоренцева как квадратичная гипербола.
Аппроксимация интегральной статистики выздоровлений рассматривалась в [2]. Применение метода наименьших квадратов привело к следующим значениям коэффициентов:
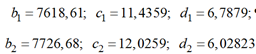
Гамма-распределение (непрерывное). Попытаемся приблизить статистику гамма-распределением. Для него плотность вероятности
(2)
где Г(k) – гамма-функция.
Математическое ожидание в (2) 
, дисперсия 
, поэтому
На рис. 3, а представлены «экспериментальные данные» (точки) и плотность вероятности гамма-распределения с параметрами, выраженными через математическое ожидание и дисперсию статистики (сплошная кривая).
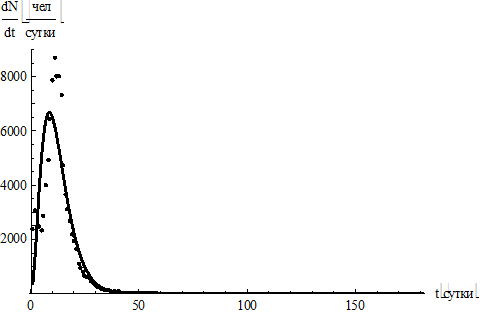
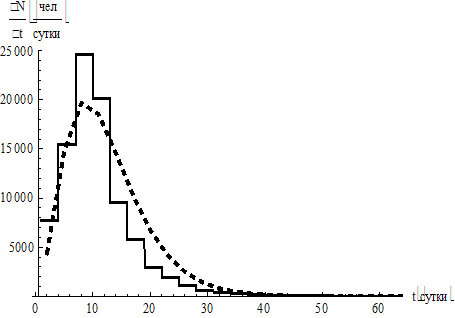
Рис. 3. Анализ гамма-распределения для амбулаторной статистики: «экспериментальные данные»
и плотность вероятности гамма-распределения (а); группировка по 3 дня (б)
Fig. 3. Analysis of the gamma distribution for outpatient statistics: “experimental data” and probability density
of the gamma distribution (а); grouping by 3 days (б)
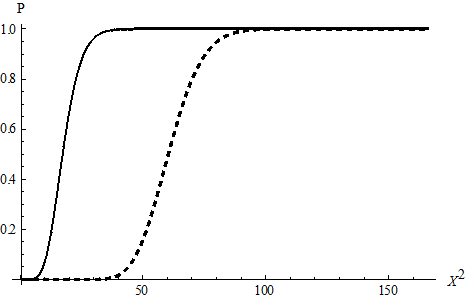
в
Рис. 3 (окончание). Анализ гамма-распределения для амбулаторной статистики:
графики вероятности P для на основе (3) (в)
Fig. 3 (ending). Analysis of the gamma distribution for outpatient statistics:
probability graphs P for based on (3) (в)
На рис. 3, б представлена группировка по 3 дня. Сплошной график гистограммы соответствует экспериментальным данным, пунктир – гамма-распределению. Улучшения укрупнение данных
не дает. Видно, что выбор теоретического распределения не является удачным. Применим критерий Пирсона, для этого вычислим величину
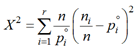
где ni – число событий из n с группировкой в r групп; 
– теоретическая вероятность в группе. Проверка гипотезы по сложному критерию Пирсона, где 2 параметра оценены (m = 2) по выборкам объемом n, а плотность 
c r – m – 1 степенями свободы имеет вид
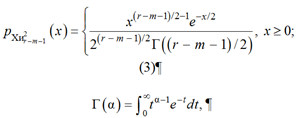
где α – аргумент гамма-функции.
Рассмотрим 2 варианта в соответствии с рис. 2, а, б:
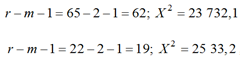
где Х определяется по приведенной выше формуле.
Графики вероятности P для 
на основе (3) (вместо таблиц) представлены на рис. 3, в: для первого варианта – сплошная линия, для второго варианта – пунктир. P-значения определяются по значениям X 2 на этих графиках, для обоих вариантов значение P приближается к 1, а для удовлетворения критерия надо попасть в левую ниспадающую часть графиков.
Отметим, что распределение Пуассона (дискретное) не подходит для рассматриваемой задачи, т. к. дисперсия для него равна математическому ожиданию, что не выполняется для статистики выздоровлений от Ковид-19.
Аппроксимация расслоенных данных
Данные по госпитальным выздоровлениям при сопутствующих диагнозах (инфекционные болезни A00-B99 и заболевания органов дыхания J00-J99) представлены на рис. 2, в, г. Имеем 3 варианта статистики:
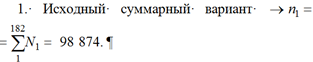
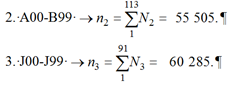
Процедура расслоения может рассматриваться как фильтрация данных.
Аппроксимация данных второго и третьего вариантов представлена на рис. 4.
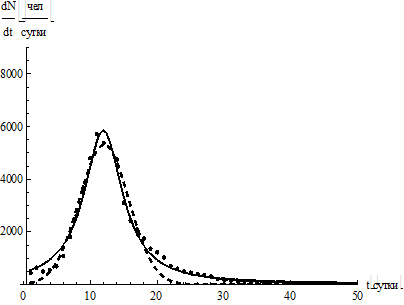
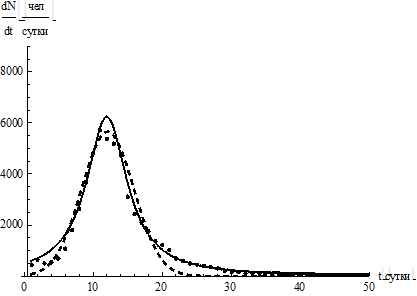
а б
Рис. 4. Аппроксимация данных второго и третьего вариантов: точки – статистические данные,
пунктир – гауссова функция; сплошная кривая – лоренцева функция:
а – аппроксимация выздоровлений при сопутствующем диагнозе A00-B99; б – J00-J99
Fig. 4. Approximation of the data of the second and third variants: points – statistical data; dotted line
is a Gaussian function; solid curve is a Lorentz function:
a – approximation of recoveries with concomitant diagnosis A00-B99; б – J00-J99
Для рис. 4, а аппроксимация гауссовой функцией (пунктир) приводит к параметрам b1 = 5 298,2,
c1 = 12,0542, d1 = 5,25086.
Аппроксимация лоренцевой функцией (сплошная кривая): b2 = 5 835,56, c2 = 11,9447,
d2 = 3,53038. Расчет среднеквадратичного уклонения (число отсчетов j = 74) проводится по формуле
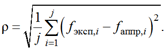(4)
Для аппроксимации гауссовой функцией ρ = 257,952, что по отношению к максимальному значению 5 712 составляет 0,0451596 (4,5 %). Наблюдаем уменьшение по сравнению с исходным вариантом без расслоения статистики, где было 0,0559 (5,6 %). Для аппроксимации лоренцевой функцией ρ = 159,044, что по отношению к максимальному значению 5 712 составляет 0,0278439 (2,7 %), – уменьшение по сравнению с основным вариантом, где было 0,0328 (3,3 %).
Для рис. 4, б аппроксимация гауссовой функцией (пунктир) приводит к следующим значениям параметров: b1 = 5 647,93, c1 = 12,0946, d1 = 5,35026. Аппроксимация лоренцевой функцией (сплошная кривая) дает: b2 = 6 235,59, c2 = 11,977, d2 = 3,58749. Расчет среднеквадратичного уклонения (число отсчетов j = 75) проводится по формуле (4).
Для аппроксимации гауссовой функцией ρ = 282,875, что по отношению к максимальному значению 5 712 составляет 0,049523 (4,95 %), – уменьшение по сравнению с основным вариантом, где было 0,0559 (5,6 %). Для аппроксимации лоренцевой функцией ρ = 165,965 или по отношению к максимальному значению 5 712 составляет 0,0290554 (2,9 %), – уменьшение по сравнению с основным вариантом, где было 0,0328 (3,3 %).
Таким образом, расслоение исходных данных по сопутствующим диагнозам улучшает аппроксимацию статистики выздоровлений как гауссовой, так и лоренцевой функциями, причем лоренцева функция лучше приближает статистические данные.
Поиск аппроксимации Джонсона
В статистической теории существует еще одна аппроксимация колоколообразной плотности вероятности, предложенная Джонсоном [10]. Процедура подбора кривой из системы Джонсона осуществляется на основе вычисления моментов высших порядков.
Наша выборка:
.
Для построения оценок удобно использовать упорядоченную выборку, где числа выстроены по возрастанию. Выражения для моментов:
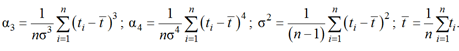
В зависимости от соотношения выбирается класс семейства кривых Джонсона:
где S, L, B – обозначение классов.
Деление на классы условное [12], в данной работе используем семейство кривых Джонсона SB, которое имеет вид
, (5)
где μ и ε – подгоночные параметры Джонсона, которые определяются ниже.
Ввиду сложности (5) метод наименьших квадратов неприменим. В нашем случае ε = 0 (или даже 1), константы предлагается определять с помощью квантилей [11].
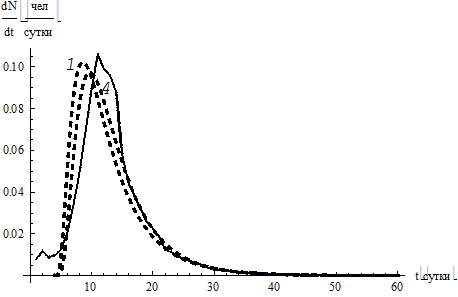
Остановимся на варианте 2 (сплошная кривая на рис. 5, а).
а б
в г
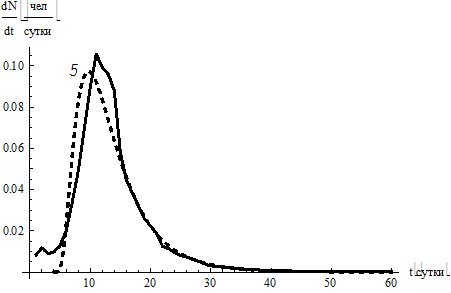
Рис. 5. Логико-эвристическая подгонка кривой Джонсона под экспериментальные данные:
а–е – варианты кривых Джонсона 1-8 в сравнении друг с другом. Значения параметров для вариантов
указаны в тексте статьи. Площади под всеми кривыми равны единице
Fig. 5. Logical-heuristic adjustment of the Johnson curve to experimental data:
a-e – the variants of Johnson curves 1-8 are presented in comparison with each other.
The parameter values for the variants are indicated in the text of the article.
The areas under all curves are equal to one
г д
Рис. 5 (окончание). Логико-эвристическая подгонка кривой Джонсона под экспериментальные данные:
а–е – варианты кривых Джонсона 1-8 в сравнении друг с другом. Значения параметров для вариантов
указаны в тексте статьи. Площади под всеми кривыми равны единице
Fig. 5 (ending). Logical-heuristic adjustment of the Johnson curve to experimental data:
a-e – the variants of Johnson curves 1-8 are presented in comparison with each other.
The parameter values for the variants are indicated in the text of the article.The areas under all curves are equal to one
Будем считать, что известен только левый предел: ε = 1, тогда оценки параметров
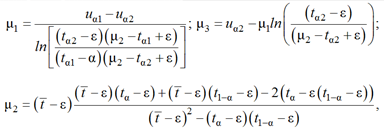
где uα – квантиль стандартного распределения, рекомендуется α1 = α = 0,05, α2 = 1 – α; tα – эмпирический квантиль ([α(N2 + 1)]-й упорядоченный по возрастанию член выборки):
В результате
.
График кривой Джонсона SB с этими значениями представлен на рис. 5, а (пунктир 1). Для сопоставления (пунктир 1) с экспериментальными данными их надо разделить на n2 (сплошная кривая). Для улучшения можно фиксировать правый конец, сейчас он получился слишком большой. Добавляем вариант с ε = 1; μ1 = 2,09088; μ2 = 3 905,0; μ3 = 12,2788 (пунктир 2) и вариант с фиксированным правым концом: ε = 0; μ1 = 2,04182; μ2 = 113,0; μ3 = 4,21455 (пунктир 3).
Анализ распределения рис. 5, а приводит к следующим выводам:
– правое крыло статистических данных может быть хорошо описано кривой Джонсона;
– на левой границе распределение резко выходит на 0 и не согласуется со статистическими данными;
– левая часть от максимума распределения и сам максимум сдвинуты влево относительно максимума статистических данных.
Формально этот сдвиг убирается, если в варианте 5, а изменить только ε, положив ε = 4 (пунктир 4, см. рис. 5, б). При отрицательных значениях ε распределение сдвигается влево.
На рис. 5, в представлен (пунктир 5) расчет с ε = 4 и оценкой параметров μ1, μ2, μ3 по усеченной статистике:
в предположении неизвестного правого конца:
α1 = α = 0,05; α2 = 1 – α;
α = 0,05 → uα1 = – uα2 = –1,645
Медиана выборки:
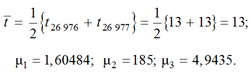
На рис. 5, г представлен (пунктир 6) расчет с ε = 6 и оценкой параметров μ1, μ2, μ3 по усеченной статистике:
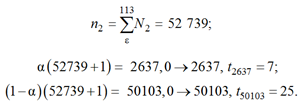
Таким образом (пунктир 6), значение ε = 6 слишком велико. Методика определения коэффициентов допускает варьирование только коэффициентов α1, α2 (в нашем случае только α1 для подстройки левой от максимума части статистики) плюс вариации 1 < ε < 4.
Далее варьируем α1 при базовом варианте ε = 4, α1 = 0,05.
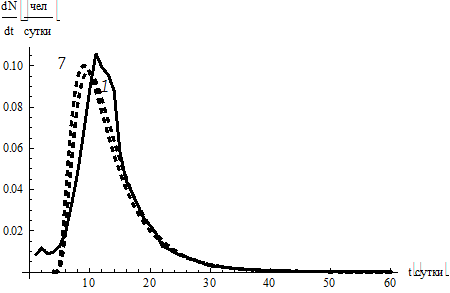
Рассмотрим вариант ε = 4, α1 = 0,08 (пунктир 7, см. рис. 5, д):
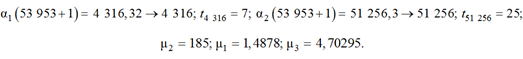
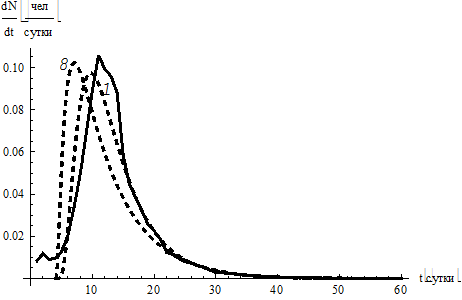
Вариант ε = 4, α1 = 0,02 (пунктир 8, см. рис. 5, е):
.
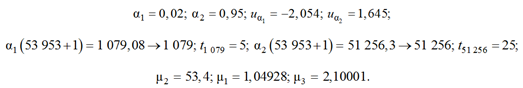Отклонение α1 в обе стороны ухудшает положение кривой Джонсона слева от максимума, при этом правое крыло всегда ложится на статистику.
Приведем в заключение расчеты коэффициентов асимметрии для 8 кривых Джонсона и статистических данных:
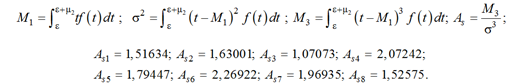
Коэффициенты асимметрии экспериментальных данных:
– исходный суммарный вариант: As = 1,73399;
– A00-B99: As = 1,94005
– J00-J99: As = 1,80561.
Кривые Джонсона асимметричны, что проявляется в наличии правого крыла и сдвиге максимумов кривых влево от максимума экспериментальных данных.
Заключение
Расслоение статистики выздоровлений по сопутствующим диагнозам улучшает аппроксимацию эмпирических данных гауссовой и лоренцевой кривыми. Такое улучшение обусловлено тем, что расслоенные статистики имеют различные математические ожидания, т. е. времена выздоровления пациентов. Расчеты показали, что во всех случаях аппроксимация лоренцевой кривой дает лучшие результаты подгонки.
Показано, что статистика выздоровлений может быть аппроксимирована более сложной подгоночной кривой Джонсона (см., например, рис. 5, б, пунктир 4). Строгое нахождение параметров подгонки кривой Джонсона под реальную статистику осложнено их количеством и сложными взаимосвязями между параметрами. По этой причине авторы применили логико-эвристический метод максимального правдоподобия, который позволил получить неплохие результаты.
Во всех вариантах применения кривой Джонсона правая часть кривой хорошо ложится на реальную статистику. Кривая Джонсона плохо описывает реальную статистику вблизи нуля и во всех случаях дает отклонение подгоночной кривой влево. Максимальные значения совпадают в наилучших вариантах с точностью 5–6 %.
1. Abdurakhimov A. Kh., Khegai L. N., Iusupova Sh. K. COVID-19 i ego oslozhneniia [COVID-19 and its complications]. Re-health journal, 2021, no. 4 (12). Available at: https://cyberleninka.ru/article/n/covid-19-i-ego-oslozhneniya (accessed: 01.02.2024).
2. Borovskii A. V., Galkin A. L., Kozlova S. S. Analiz statisticheskikh dannykh ambulatornogo lecheniia COVID-19 po gorodu Irkutsku za 2020–2021 gg. [Analysis of statistical data on outpatient treatment of COVID-19 in the city of Irkutsk for 2020-2021]. System Analysis & Mathematical Modeling, 2023, vol. 5, no. 4, pp. 494-504. DOI:https://doi.org/10.17150/2713-1734.2023.5(4).494-504.
3. Borovskii A. V., Il'inykh N. N., Kozlova S. S. Ma-tematicheskaia model' dlia skorosti zarazheniia SARS-COV-2 v neinfektsionnykh bol'nitsakh na primere goroda Irkutska [A mathematical model for the rate of infection of SARS-COV-2 in non-infectious hospitals using the example of the city of Irkutsk]. System Analysis & Mathematical Modeling, 2022, vol. 4, no. 3, pp. 187-199. DOI:https://doi.org/10.17150/2713-1734.2022.4(3).187-199.
4. Tamm M. V. Koronavirusnaia infektsiia v Moskve: prognozy i stsenarii [Coronavirus infection in Moscow: forecasts and scenarios]. Farmakoekonomika. Sovremennaia farmakoekonomika i farmakoepidemiologiia, 2020, vol. 13, no. 1, pp. 43-51. DOI:https://doi.org/10.17749/2070-4909.2020.13.1.43-51.
5. Ivanov M. V. Matematicheskoe modelirovanie protsessa pandemii. Teoriia i praktika [Mathematical modeling of the pandemic process. Theory and practice]. Institut razvitiia strategicheskikh initsiativ, 2020, 30 aprelia. Available at: https://indsi.ru/2020/04/30 (accessed: 01.02.2024).
6. Golovinskii P. A. Matematicheskoe modelirovanie rasprostraneniia virusov s dlinnoi inkubatsionnoi fazoi v tesnom mire [Mathematical modeling of the spread of viruses with a long incubation phase in a small world]. Vestnik Voronezhskogo gosudarstvennogo universiteta. Seriia: Sistemnyi analiz i informatsionnye tekhnologii, 2020, no. 2, pp. 5-14. DOI:https://doi.org/10.17308/sait.2020.2/2909.
7. Arenas A., Cota W., Gómez-Gardeñes J., Gomez S. Modeling the Spatiotemporal Epidemic Spreading of COVID-19 and the Impact of Mobility and Social Distancing Interventions. Physical Review X, 2020, vol. 10, iss. 4, p. 041055.
8. Riyapan P., Shuaib S. E., Intarasit A. A Mathematical Model of COVID-19 Pandemic: A Case Study of Bangkok, Thailand. Computational and Mathematical Methods in Medicine, 2021, vol. 9, pp. 1-11. DOI:https://doi.org/10.1155/2021/6664483.
9. Xiao-Ping Li, Ye Wang, Muhammad Altaf Khan, Mohammad Y. Alshahrani, Taseer Muhammad. A Dynamical Study of SARS-COV-2: A Study of third Wave. Results in Physics, 2021, vol. 29, p. 104705. DOI:https://doi.org/10.1016/j.rinp.2021.104705.
10. Johnson N. L. Systems of frequency curves generated by methods of translation. Biometrika, 1949, vol. 36, no. 1/2, pp. 149-176.
11. Kobzar' A. I. Prikladnaia matematicheskaia statistika [Applied mathematical statistics]. Moscow, FIZMATLIT Publ., 2006. 816 p.
12. Borbats' N. M., Shkolina T. V. Protsedura podbora krivoi iz sistemy Dzhonsona metodami protsentilei i maksimal'nogo pravdopodobiia – naimen'shikh kvadratov [The procedure for selecting a curve from the Johnson system using percentile and maximum likelihood methods – the name of the squares]. System Analysis & Mathematical Modeling, 2023, vol. 5, no. 4, pp. 477-492. DOI:https://doi.org/10.17150/2713-1734.2023.5(4).476-493.
