graduate student from 01.01.2020 until now
Russian Federation
The technique based on the use of a hybrid optimization method to solve the feature selection problem for the Cox regression model is proposed. The hybrid optimization method includes two metaheuristic methods: the ant colony optimization and the genetic algorithm. The ant colony optimization used as the basic algorithm that solves the main optimization problem. The genetic algorithm solves the problem of finding the optimal set of parameters for the ant algorithm improving its performance. The method is modified and adapted to solve the problem under consideration. The key feature of adaptation is the deposition of pheromones on the vertices rather than on the edges of the graph, as well as the method for calculating the assessment of heuristic information about each vertex. A fitness target function was constructed that determines the quality of solutions to the feature selection problem and is based on an assessment of the performance of the Cox model with a selected set of parameters. The concordance index (c-index) was used to evaluate the Cox model. The efficiency of the methodology is shown using the implemented program using the example of a database of recidivism. For the database used, the most significant sets of features were obtained that have the greatest impact on the quality of training of the survival analysis model.
survival analysis, feature selection, Cox model, ant colony optimization, genetic algorithm
Введение
Анализ выживаемости – это совокупность статистических методов, использующихся для оценки вероятности наступления события, при наличии цензурированных наблюдений. Методы работают с данными, содержащими временную характеристику, которой является время от начала наблюдения до наступления терминального события или выхода объекта из наблюдения. Терминальным событием является наступление критического состояния рассматриваемой системы, ведущего к ее отказу или потере важного в рамках задачи функционала. Примерами терминальных событий в зависимости от предметной области могут являться рецидивы заболевания, летальные исходы пациентов, отказ оборудования, отток клиентов, банкротство компаний. Особенностью и преимуществом анализа выживаемости является допущение использования данных, вышедших из наблюдения, называемых цензурированными данными. В связи с этим класс методов анализа выживаемости находит широкое применение в медицинских, инженерных, экономических и социальных науках [1]. Анализ выживаемости используется для моделирования и анализа распределения времени наступления терминальных событий [2]. Одной из моделей анализа выживаемости, используемых в прикладных областях, является регрессионная модель Кокса [3], которая является объектом данного исследования.
Для построения точных прогнозов и выявления закономерностей в рамках задач анализа выживаемости важную роль играет оптимизация. Одной из задач оптимизации, имеющих приложение к модели Кокса, является задача выбора признаков, заключающаяся в поиске оптимального набора признаков, по которому можно сделать прогноз. Это помогает экспертам сделать вывод о том, какие признаки имеют большую прогностическую значимость. Кроме того, выбор признаков позволяет сократить количество признаков для обучения модели, что увеличивает скорость работы программы. Выбор признаков также позволяет работать с разреженными данными [4]. В связи с тем, что задача выбора признаков может быть сформирована в терминах оптимизации, для ее решения могут быть использованы классические или усовершенствованные методы оптимизации. Одним из таких методов является метаэвристический гибридный метод оптимизации, основанный на муравьином и генетическом алгоритмах. Этот метод является предметом исследования.
Из вышесказанного следует, что модель Кокса имеет широкую область применения, а задача выбора признаков для модели является востребованной. Построение методики, позволяющей решать задачу выбора признаков в регрессионной модели Кокса, является актуальной задачей. В работе впервые продемонстрирована возможность приложения рассматриваемого гибридного алгоритма оптимизации для решения задачи выбора признаков для модели Кокса, чем обусловлена научная новизна исследования.
Целью данного исследования является разработка методики решения задачи выбора признаков для модели Кокса, основанной на использовании гибридного метода оптимизации. Цель определяет задачи, которые были решены в работе:
– сформулированы задачи выбора признаков для модели Кокса и построена функция приспособленности, оценивающая результаты прогнозов модели Кокса;
– адаптирован гибридный метод оптимизации к задаче выбора признаков;
– разработана программа, реализующая методику; апробирован результат и продемонстрирована эффективность разработанной методики.
Результаты работы методики представлены на базе Rossi о рецидивах преступлений [5].
Задача выбора признаков
Задача выбора признаков важна для решения прикладных задач. Экспертам в прикладных областях, использующим модель анализа выживаемости, важно понимать, какой набор признаков является существенным для составления прогноза. Важность признаков позволяет экспертам делать соответствующие выводы о модели и оценивать риски. Кроме того, выбор признаков позволяет снизить размерность пространства данных [6]. Снижение размерности актуально для работы с разреженными данными, в условиях работы с нехваткой данных. Снижение размерности данных может повысить производительность программы [7].
Так как для решения задачи используется метод оптимизации, необходимо сформулировать ее в терминах задач оптимизации, явно построив целевую функцию.
Пусть S обозначает набор данных для обучения с n экземплярами; F – множество всех признаков f1, f2, ..., fp. Определим некоторое подмножество признаков Et ⊂ F. Функция c(S, Et) вычисляет индекс согласованности (c-индекс) регрессионной модели Кокса, обученной S экземплярами с Et признаками. Количество признаков, используемых при обучении, определяется величиной |Et| – мощностью множества Et. Необходимо найти решение
Et такое, что
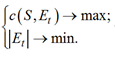 (1)
(1)
Условия (1) порождают задачу многокритериальной оптимизации, которая может быть сведена
к задаче линейной оптимизации, например с помощью добавления регуляризационного множителя [8]:
![]()
где L(S, Et) – значение функции потерь; α – коэффициент, используемый для баланса слагаемых L(S, Et) и ![]() .
.
В работе [8] качество модели оценивается с помощью функции потерь, т. к. этот подход является общим для любой обучающейся модели. Однако для оценки качества прогнозов моделей анализа выживаемости часто используется индекс согласованности (c-индекс). В отличие от функции потерь, индекс увеличивается с улучшением модели, поэтому функция приспособленности построена следующим образом:
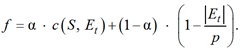 (2)
(2)
Задача заключается в поиске максимума целевой функции f.
Классическим подходом к решению задачи является ранжирование признаков по их единичному вкладу в модель. Однако такой подход не учитывает наличие скрытых зависимостей параметров, их корреляцию, а также возможность улучшения прогноза в совокупности не значащих по отдельности признаков.
Модель Кокса
В статье рассматривается одна из наиболее популярных моделей анализа выживаемости [9], называемая регрессионной моделью Кокса. Она относится к классу моделей пропорциональных рисков. Функция риска для модели Кокса описывается в следующем виде:
![]()
где β – вектор влияния признаков; Xi ∈ S – экземпляр данных; λ0 – базовый риск, не зависящий от признаков.
Логарифм функции риска для одного образца представляет линейную комбинацию его признаков, поэтому модель устанавливает явную взаимосвязь между признаками образца и временем наступления терминального события:

Следует отметить, что соотношение рисков между ковариатами не зависит от времени:
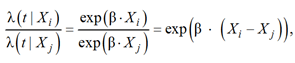
в этом заключается пропорциональность рисков.
В предложенной методике используется алгоритм, относящийся к классу метаэвристических гибридных алгоритмов. В основе алгоритма лежит алгоритм муравьиной колонии. Для определения оптимальных параметров муравьиного алгоритма используется генетический алгоритм.
Алгоритм муравьиной колонии. Алгоритм муравьиной колонии, относящийся к классу роевого интеллекта, является метаэвристическим алгоритмом комбинаторной оптимизации. Алгоритм имитирует поведение муравьев во время поиска и добычи пищи.
Муравьи в естественных условиях обитания находят источник пропитания случайным образом. Когда один из муравьев находит пищу, он возвраща-
ется в колонию и оставляют следы из феромонов. Другие муравьи, если обнаружат след, в большинстве случаев пойдут по нему. Муравьи, если им удастся добраться до источника пищи, также начнут оставлять феромоны на обратном пути, делая путь до пищи более привлекательным для всей колонии. Феромон со временем начинает испаряться, пройденные тропы становятся менее привлекательными для муравьев. Чем короче путь, тем меньше феромона успевает испариться.
В широком смысле алгоритмы муравьиной колонии являются классом похожих алгоритмов и методов, моделирующих способ добычи муравьями пищи. Одной из первых реализаций модели является простой муравьиный алгоритм. Алгоритм восприимчив к параметрам: коэффициенту испарения, количеству откладываемого феромона, чувствительности муравья к феромонам. Существует несколько способов определения параметров, которые можно разделить на две группы: статические и динамические. Статические способы задают первоначальные параметры, не изменяющиеся во время работы алгоритма. Как правило, первоначальные параметры находятся экспериментально. Динамические или адаптационные способы позволяют менять значения параметров во время работы алгоритма, приближая их к оптимальным. В работе [10] представлен гибридный адаптационный метод, основанный на простом муравьином алгоритме, и показана его эффективность, поэтому он выбран для решения задачи.
Следует отметить, что алгоритмы муравьиной колонии используют для решения задач оптимизации на графах, поэтому поставленную задачу необходимо сформулировать и в терминах теории графов.
Генетический алгоритм. Генетический алгоритм относится к классу метаэвристических алгоритмов, моделирующих естественный отбор. Так же, как простой муравьиный алгоритм, генетический алгоритм используется для задач комбинаторной оптимизации. Подобно муравьиному, генетический алгоритм формирует класс аналогичных алгоритмов, использующих идею моделирования естественного отбора [11]. В таких алгоритмах потенциальное решение некоторой задачи называется особью, или индивидом, который кодируется особым образом (в простейшем случае – двоичным числом). Совокупность особей, которые являются потенциальными решениями, называется популяцией.
Поиск оптимального решения задачи осуществляется при последовательном преобразовании одного конечного множества решений в другое с использованием генетических операторов отбора (селекции), скрещивания (кроссинговера) и мутации.
Оператор селекции отбирает особей, формируя новую популяцию, для последующего применения остальных операторов. Как правило, отбираются особи, решение которых наиболее близко к оптимальному.
Существует множество способов реализации оператора селекции [12].
Оператор скрещивания создает новую популяцию особей, используя попарное преобразование особей текущей популяции. Он некоторым образом объединяет информацию о двух особях для создания новой. Как и оператор выбора, оператор скрещивания может быть реализован различными способами. Этот оператор имеет свою собственную реализацию в зависимости от типа данных, которые обрабатывает алгоритм [13].
Оператор мутации позволяет получать принципиально новые особи. Обычно оператор мутации изменяет какую-то часть решения с небольшой вероятностью [12].
Преимущество алгоритма заключается в том, что эволюционная идея может быть применена в разных задачах и разными способами [14]. Каждый из операторов имеет большое количество реализаций, которые могут быть использованы для решения разных задач.
В данной работе построенная функция приспособленности (2) определяет задачу оптимизации, которая может быть решена метаэвристическими методами. В работе использован и адаптирован метод, основная идея которого описана в [10]. Как известно, алгоритм муравьиной колонии применяется к задачам на графах [15], поэтому необходимо сформулировать задачу выбора признаков в терминах теории графов. Как показано в статьях [16, 17], задачу можно сформулировать следующим образом.
Определим полносвязный граф G(V, E), где V – множество вершин, представляющих признаки. Очевидно, |V| = p необходимо найти множество Et, удовлетворяющее условиям (1).
Важную роль в алгоритме муравьиной колонии и, следовательно, в гибридном алгоритме играют параметры. В используемом алгоритме каждый муравей k имеет разный набор параметров αk, βk, Qk, αk – чувствительность муравьев к феромонам. Она определяет степень эксплуатации муравьями найденных решений. βk является эвристической чувствительностью, устанавливающей уровень эксплуатации эвристической информации. Qk – интенсивность феромона, которая определяет количество феромона, которое отложит муравей в процессе поиска решения. Алгоритм также имеет набор статических параметров: количество муравьев n, скорость испарения ρ, постоянная величина феромонов τ.
Учитывая особенность задачи выбора признаков для модели Кокса, необходимо модифицировать алгоритм. Классический подход подразумевает решение задач на графах со взвешенными ребрами. В графе G ребра не имеют веса, однако наборы вершин имеют. Вес набора или множества вершин рассчитывается как c-индекс модели Кокса, обученной на признаках, соответствующих вершинам из набора.
Каждый муравей выбирает вершину стохастически по правилу
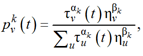
где ![]() – вероятность выбора вершины v муравьем k на итерации t; τv(t) – количество отложенного феромона на вершине v на итерации t; ηv – эвристическая информация, которая вычисляется как ηv = c(S,{v}) – c-индекс модели Кокса, обученной для одного признака v; u – любая другая вершина, отличающаяся от v и не входящая в построенный на итерации t путь. Такой способ выбора эвристической информации обусловлен тем, что ранжирование признаков по их одиночному вкладу является одной из распространенных стратегий решения задачи выбора признаков модели Кокса.
– вероятность выбора вершины v муравьем k на итерации t; τv(t) – количество отложенного феромона на вершине v на итерации t; ηv – эвристическая информация, которая вычисляется как ηv = c(S,{v}) – c-индекс модели Кокса, обученной для одного признака v; u – любая другая вершина, отличающаяся от v и не входящая в построенный на итерации t путь. Такой способ выбора эвристической информации обусловлен тем, что ранжирование признаков по их одиночному вкладу является одной из распространенных стратегий решения задачи выбора признаков модели Кокса.
Каждый муравей выделяет феромон в соответствии с правилом

где Ek – множество вершин, выбранных муравьем k.
После того как каждый муравей построил путь, параметры αk, βk, Qk пересчитываются с помощью генетического алгоритма. Генетический алгоритм последовательно применяет к параметрам три оператора – выбора, кроссинговера и мутации. Новые параметры используются для дальнейшего поиска муравьиным алгоритмом оптимального набора признаков для обучения модели Кокса.
В работе используется набор данных Rossi о рецидивах преступлений. Этот набор данных представлен в [5]. Набор данных содержит информацию о 432 заключенных, которые были выпущены из тюрем штата Мэриленд в 1970-х гг. и за которыми велось наблюдение в течение года после их освобождения. Из числа освобожденных заключенных, выбранных случайным образом, половине была оказана финансовая помощь в рамках экспериментальной социологической программы, в то время как другой половине – нет. Социологическая программа была направлена на снижение частоты рецидивов преступлений. Набор данных можно использовать для модели Кокса и, как следствие, для проверки предложенной методики. В качестве временной характеристики используется количество недель с момента ареста, а в качестве терминального события – информация о рецидиве.
Каждый образец данных имеет 9 характеристик (признаков):
– “week”: неделя с момента первого ареста после освобождения или цензурирования;
– “arrest”: признак, указывающий, был ли человек арестован повторно. Булевая характеристика, указывающая на наступление терминального события;
– “fin”: признак, указывающий на наличие финансовой поддержки;
– “age”: возраст, при котором заключенный был освобожден;
– “race”: раса арестованного;
– “wexp”: признак, указывающий на наличие у заключенного какого-либо опыта работы;
– “mar”: семейное положение заключенного на момент освобождения;
– “paro”: признак, указывающий, освобожден ли заключенный условно-досрочно;
– “prio”: общее количество судимостей, вынесенных ранее до вынесения текущего приговора.
Набор данных использовался в исследовании по нескольким причинам. Во-первых, набор не содержит разреженных данных, поэтому его удобно использовать для проверки алгоритма. Во-вторых, данные не содержат большого количества признаков, что позволяет легко реализовать поиск оптимального набора признаков методом перебора, чтобы проверить корректность работы алгоритма. Следует отметить, что база данных включена в программные пакеты, которые работают с анализом выживаемости. Также существуют различные исследования моделей анализа выживаемости на текущем наборе данных, что позволяет исследователю сравнивать результаты.
Методика реализована на языке программирования Python. Использовался пакет CoxPHFitter из библиотеки Lifelines. Для хранения и обработки данных использовалась программная библиотека Pandas. Также использовался набор данных Rossi.
Чтобы оценить результаты работы предложенной методики, модель Кокса была обучена на данных со всеми возможными комбинациями признаков. Лучшие комбинации показаны в табл. 1.
Таблица 1
Table 1
Наборы признаков с самым высоким значением c-индекса
Feature sets with the highest c-index value
|
c-index модели Кокса |
|
|
“age”, “prio” |
0,63315 |
|
“age”, “race”, “paro”, “prio” |
0,63346 |
|
“fin”, “age”, “mar’”, “prio” |
0,6335 |
|
“fin”, “age”, “mar”, “paro”, “prio” |
0,63367 |
|
“age”, “mar”, “prio” |
0,63397 |
|
“fin”, “wexp”, “race”, “mar”, “prio” |
0,63402 |
|
“fin”, “wexp”, “race”, “mar”, “paro”, “prio” |
0,63413 |
|
“age”, “paro”, “prio” |
0,63434 |
|
“age”, “race”, “mar”, “paro”, “prio” |
0,63465 |
|
“fin”, “age”, “race”, “mar”, “paro”, “prio” |
0,63495 |
|
“fin”, “age”, “race”, “mar”, “prio” |
0,63497 |
|
“age”, “mar”, “paro”, “prio” |
0,63571 |
|
“wexp”, “age”, “paro”, “prio” |
0,63586 |
|
“wexp”, “age”, “race”, “mar”, “prio” |
0,63615 |
|
“wexp”, “age”, “mar”, “paro”, “prio” |
0,63617 |
|
“wexp”, “age”, “prio” |
0,63625 |
|
“wexp”, “age”, “race”, “prio” |
0,6364 |
|
“wexp”, “age”, “mar”, “prio” |
0,63642 |
|
“wexp”, “age”, “race”, “mar”, “paro”, “prio” |
0,63644 |
|
“wexp”, “age”, “race”, “paro”, “prio” |
0,63677 |
|
“fin”, “wexp”, “age”, “race”, “paro”, “prio” |
0,63757 |
|
“fin”, “wexp”, “age”, “paro”, “prio” |
0,63764 |
|
“fin”, “wexp”, “age”, “race”, “prio” |
0,63872 |
|
“fin”, “wexp”, “age”, “mar”, “paro”, “prio” |
0,63903 |
|
“fin”, “wexp”, “age”, “prio” |
0,6393 |
|
“fin”, “wexp”, “age”, “race”, “mar”, “paro”, “prio” |
0,64033 |
|
“fin”, “wexp”, “age”, “mar”, “prio” |
0,6407 |
|
“fin”, “wexp”, “age”, “race”, “mar”, “prio” |
0,64194 |
Примечательно, что модель, обученная на шести признаках, имеет более высокий c-индекс, чем модель, обученная на всех семи. Это связано с тем, что некоторые признаки в сочетании с другими могут ухудшить результат обучения, что приводит к проблеме переобучения. Таким образом, чрезмерный объем данных может привести к ошибке [18, 19].
Основываясь на результатах табл. 1, можно сказать, что возраст заключенного и его общее количество судимостей, безусловно, являются наиболее важными признаками. Эти два признака входят во все комбинации с высоким индексом соответствия.
Результаты работы методики в зависимости от регуляризационного коэффициента α, используемого для баланса слагаемых (2), приведены в табл. 2.
Таблица 2
Table 2
Лучший набор признаков в зависимости от регуляризационного коэффициента
The best set of features depending on the regularization coefficient
|
Регуляризационный коэффициент α |
Набор признаков |
Значение функции приспособленности f |
c-индекс |
|
0,8 |
“age” |
0,66234 |
0,61364 |
|
0,9 |
“age”, “prio” |
0,64127 |
0,63315 |
|
0,99 |
“fin”, “wexp”, “age”, “prio” |
0,63719 |
0,6393 |
|
1,0 |
“fin”, “wexp”, “age”, “race”, “mar”, “prio” |
0,64194 |
0,64194 |
Для того чтобы значение индекса соответствия было приоритетнее, чем количество признаков, необходимо, чтобы коэффициент α был достаточно близок к 1. Поэтому в работе использовались следующие значения коэффициента: 0,8; 0,9; 0,99; 1,0. В последнем случае, когда коэффициент равен 1, алгоритм находит лучшую комбинацию признаков независимо от их количества.
В работе используются следующие параметры гибридного алгоритма: ρ = 0,5, Q0 = 25, n = 12, количество итераций in = 10. При низком значении коэффициента регуляризации значительным оказался только один признак – “age” (возраст). С увеличением коэффициента увеличивается и количество признаков. А при коэффициенте, равном 1, найден лучший набор признаков. Результаты алгоритма согласуются с результатами из табл. 1. Видно, что найдены лучшие комбинации для каждого количества признаков.
Следует отметить, что структура алгоритма позволяет менять функцию приспособленности таким образом, чтобы поиск осуществлялся только по необходимому количеству признаков. Другими словами, муравьи будут искать наборы, состоящие только из определенного количества признаков. Однако в работе используется балансирующий коэффициент, т. к. на практике может быть неизвестно, сколько значимых признаков должно быть.
Примечательна быстрая сходимость алгоритма к лучшему набору признаков (в среднем – менее 10 итераций). Более того, алгоритм находит лучший набор независимо от начальных параметров. Такая устойчивость к первоначальным параметрам обусловлена работой генетического алгоритма, который находит подходящие параметры для муравьиного.
Тем не менее, алгоритм требует значительного количества обучений модели Кокса для каждого муравья и для каждого построенного им пути, поэтому ощутимый выигрыш может быть получен при достаточно большом количестве исходных признаков.
Будущие направления и возможности для исследований
Методика, предложенная в работе, демонстрирует идею применения стабильного гибридного алгоритма оптимизации к задаче выбора признаков для модели анализа выживаемости. Подход может быть применен не только к регрессионной модели Кокса, но и к другим моделям выживаемости. Более того, выбор модели также может быть одним из параметров оптимизации.
В следующих статьях этой темы можно установить влияние критерия оценки модели на работу алгоритма. В качестве функции оценивания можно использовать не только индекс соответствия [20, 21], использованный в [22] или этой работе, но и функцию потерь, как это делается в некоторых других работах [8, 23, 24], или показатель стабильности SMA-Count [25, 26].
Одной из особенностей муравьиных алгоритмов является использование стигметрии – откладывания феромона. Это можно использовать не только для задачи выбора объектов, но и для их ранжирования. Можно предположить, что чем больше феромона откладывается в вершинах графа, тем более значимым является признак, представленный в этой вершине. Однако алгоритм не слишком устойчив к количеству оставляемого на вершинах графа феромона, поэтому каждый запуск программы порождает разное количество феромона на вершинах. Это можно исправить, изменив функцию выбора вершин и функцию откладывания феромона.
Предложенная методика гибридного алгоритма муравьиной колонии с генетическим подходом решает задачу выбора признаков для регрессионной модели Кокса. Выбор признаков актуален при решении прикладных задач. Методика протестирована на данных о рецидивах преступлений.
Продемонстрировано, что методика способна решать задачу нахождения лучшей комбинации признаков за приемлемое число итераций. Регуляризационный коэффициент позволил уменьшить количество признаков, что, с одной стороны, ухудшает качество модели, но, с другой стороны, снижает ее сложность.
Таким образом, можно сделать вывод, что класс муравьиных алгоритмов может быть использован для решения задачи выбора признаков в моделях анализа выживаемости, выбор признаков рассматривать в качестве целевой функции. Модификация муравьиного алгоритма, включающая использование генетического, не влияет на структуру подхода к решению задачи, однако нахождение оптимальных параметров делает алгоритм более надежным и стабильным, что, несомненно, является его преимуществом для решения поставленной задачи. В ходе работы была построена функция приспособленности для задачи оптимизации, внесена модификация в работу гибридного алгоритма, чтобы его можно было применить к поставленной задаче, и разработана программа, реализующая предложенную методику.
1. Archetti A., Lomurno E., Lattari F., Martin A., Matteucci M. Heterogeneous Datasets for Federated Survival Analysis Simulation. Companion of the 2023 ACM/SPEC International Conference on Performance Engineering, 2023. DOI:https://doi.org/10.1145/3578245.3584935.
2. George B., Seals S., Aban I. Survival analysis and regression models. J. Nucl. Cardiol., 2014, pp. 686-694. DOI:https://doi.org/10.1007/s12350-014-9908-2.
3. Atlam M., Torkey H., El-Fishawy N., Salem H. Coronavirus disease 2019 (COVID-19): survival analysis using deep learning and Cox regression model. Pattern Anal. Applic., 2021, no. 24 (3), pp. 993-1005. DOI:https://doi.org/10.1007/s10044-021-00958-0.
4. Chen X., Yuan G., Nie F., Ming Z. Semi-Supervised Feature Selection via Sparse Rescaled Linear Square Regression. IEEE Transaction on Knowledge Discovery and Data Engineering 32, 2018. P. 165–176. DOI:https://doi.org/10.1109/TKDE.2018.2879797.
5. Rossi P. H., Berk R. A., Lenihan K. J. Money, work and crime: some experimental results. New York, Academic Press, 1980. 336 p.
6. Abd Elaziz M., Dahou A., Abualigah L., Yu L., Alshinwan M., Khasawneh A. M., Lu S. Advanced metaheuristic optimization techniques in applications of deep neural networks: a review. Neural Computing and Applications, 2021, pp. 1-21.
7. Ewees A. A., Abualigah L., Yousri D., Algamal Z. Y., Al-qaness M. A. A., Ali Ibrahim R., Elazis M. A. Improved Slime Mould Algorithm based on Firefly Algorithm for feature selection: A case study on QSAR model. Engineering with Computers, 2022, vol. 38 (Suppl 3), pp. 2407-2421. DOI:https://doi.org/10.1007/s00366-021-01342-6.
8. Ewees A. A., Al-qaness M. A. A., Abualigah L., Oliva D., Algamal Z. Y., Anter A. M., Ali Ibrahim R., Ghoniem R. M., Elaziz M. A. Boosting Arithmetic Optimization Algorithm with Genetic Algorithm Operators for Feature Selection: Case Study on Cox Proportional Hazards Model. Mathematics, 2021, vol. 9 (18), p. 2321. DOI:https://doi.org/10.3390/math9182321.
9. Archetti A., Ieva F., Matteucci M. Scaling survival analysis in healthcare with federated survival forests: A comparative study on heart failure and breast cancer ge-nomics. Future Generation Computer Systems, 2023, vol. 149 (6). DOI:https://doi.org/10.1016/j.future.2023.07.036.
10. Blagoveshchenskaya E. A., Mikulik I. I., Strüng-mann L. H. Ant colony optimization with parameter update using a genetic algorithm for travelling salesman problem. Models and Methods for Researching Information Systems in Transport 2020 (MMRIST 2020), 2021, pp. 20-25.
11. Brand M., Masuda M., Wehner N., Xiao-Hua Y. Ant Colony Optimization algorithm for robot path planning. International Conference On Computer Design and Applications, 2010. DOI:https://doi.org/10.1109/ICCDA.2010.5541300.
12. Whitley D. Next Generation Genetic Algorithms: A User’s Guide and Tutorial. Handbook of Metaheuristics. International Series in Operations Research & Management Science. Cham, Springer, 2019. Vol. 272. DOI:https://doi.org/10.1007/978-3-319-91086-4\_8.
13. Katoch S., Chauhan S. S., Kumar V. A review on genetic algorithm: past, present, and future. Multimedia Tools and Applications, 2021, vol. 80 (4), pp. 8091-8126. DOI:https://doi.org/10.1007/s11042-020-10139-6.
14. Singh G., Gupta N. A Study of Crossover Operators in Genetic Algorithm. Springer Tracts in Nature-Inspired Computing. Singapore, Springer, 2022. DOI:https://doi.org/10.1007/978-981-16-3128-3\_2.
15. Lambora A., Gupta K., Chopra K. Genetic Algorithm – A Literature Review. 2019 International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon) (Faridabad, India, 2019). Pp. 380-384. DOI:https://doi.org/10.1109/COMITCon.2019.8862255.
16. Zhou X., Gui W., Heidari A. A., Cai Z., Liang G., Chen H. Random following ant colony optimization: Con-tinuous and binary variants for global optimization and feature selection. Applied Soft Computing, 2023, vol. 144 (6), p. 110513. DOI:https://doi.org/10.1016/j.asoc.2023.110513.
17. Tabakhi S., Moradi P., Akhlaghian F. An unsupervised feature selection algorithm based on ant colony optimization. Engineering Applications of Artificial Intelligence, 2014, vol. 32, pp. 112-123. DOI:https://doi.org/10.1016/j.engappai.2014.03.007.
18. Katzmann A., Mühlberg A., Sühling M., Nörenberg D., Maurus S., Holch J. W., Heinemann V., Gross H.-M. Computed Tomography Image-Based Deep Survival Regression for Metastatic Colorectal Cancer Using a Non-proportional Hazards Model. Predictive Intelligence in Medicine, 2019, pp. 73-80. DOI:https://doi.org/10.1007/978-3-030-32281-6\_8.
19. Xu L., Cai L., Zhu Z., Chen G. Correction: Comparison of the cox regression to machine learning in predicting the survival of anaplastic thyroid carcinoma. BMC Endocrine Disorders, 2023, vol. 23 (1), p. 174. DOI:https://doi.org/10.1186/s12902-023-01431-1.
20. Longato E., Vettoretti M., Di Camillo B. A practical perspective on the concordance index for the evaluation and selection of prognostic time-to-event models. Journal of Biomedical Informatics, 2020, vol. 108. DOI:https://doi.org/10.1016/j.jbi.2020.103496.
21. Pencina M. J., D’Agostino R. B. Overall C as a measure of discrimination in survival analysis: model specific population value and confidence interval estimation. Statistics in Medicine, 2004, vol. 23 (13), pp. 2109-2123. DOI:https://doi.org/10.1002/sim.1802.
22. Yin Q., Chen W., Zhang C., Wei Z. A convolutional neural network model for survival prediction based on prognosis-related cascaded Wx feature selection. Laboratory investigation, 2022, vol. 102 (10), pp. 1064-1074. DOI:https://doi.org/10.1038/s41374-022-00801-y.
23. Ewees A. A., Algamal Z. Y., Abualigah L., Alqaness M. A. A., Yousri D., Ghoniem R. M., Abd Elaziz M. A Cox Proportional-Hazards Model Based on an Improved Aquila Optimizer with Whale Optimization Algorithm Operators. Mathematics Mathematics, 2022, vol. 10 (8), p. 1273. DOI:https://doi.org/10.3390/math10081273.
24. Bichindaritz I., Liu G., Bartlett C. Survival predic-tion of breast cancer patient from gene methylation data with deep LSTM network and ordinal cox model. Proceedings of the Thirty-Third International Florida Artificial Intelligence Research Society Conference (FLAIRS 2020). Available at: https://cdn.aaai.org/ocs/18461/18461-79401-1-PB.pdf (accessed: 12.01.2024).
25. Bommert A., Rahnenführer J. Adjusted Measures for Feature Selection Stability for Data Sets with Similar Features. Machine Learning, Optimization, and Data Science. Lecture Notes in Computer Science (LOD). Cham, Springer, 2020. Vol. 12565. DOI:https://doi.org/10.1007/978-3-030-64583-0\_19.
26. Bommert A., Welchowski T., Schmid M., Rah-nenführer J. Benchmark of filter methods for feature selection in high-dimensional gene expression survival data. Briefings in Bioinformatics, 2021, vol. 23 (4). DOI:https://doi.org/10.1093/bib/bbab354.















