Russian Federation
Russian Federation
Russian Federation
One of the directions of scientific and technological progress at sea-based facilities is the use of electrical technologies based on nonlinear elements. It is revealed that the use of such technologies leads to a deterioration in the quality of electricity, mainly due to higher harmonic. The results of theoretical and experimental studies of the higher harmonic components of voltage and current occurring during the operation of ship frequency-controlled asynchronous electric drives are presented. During operation of a frequency-controlled electric drive high current harmonics of mainly 5, 7, 11, 13 orders are emitted into the power supply network, which is due to the presence of a six-phase rectifier. This leads to distortion of the sinusoid of the supply voltage, since the higher harmonic components of the current, propagating through the electrical network, create corresponding voltage drops on its elements. Along with the main harmonic of the voltage of a given frequency, the higher harmonic components of the voltage flow from the autonomous voltage inverter to the stator winding of the asynchronous electric motor, which causes the higher current harmonics and torques of the forward and reverse current sequences in the stator and rotor windings. As a result additional heating of the stator and rotor windings occurs and vibrations of the asynchronous motor shaft at frequencies of 300 and 600 Hz occur. A method for measuring the vibration of a frequency-controlled asynchronous electric drive from the interaction of the moments of the reverse and forward sequences has been developed and experimentally confirmed. A method for calculating the intrinsic frequency of oscillations of the asynchronous motor-load machine system is proposed, confirmed by the example of a laboratory installation. To accurately calculate the natural frequency of the oscillatory system, it is necessary to experimentally measure the moments of inertia of the rotor of an asynchronous motor and the armature of a DC motor.
frequency-controlled asynchronous electric drive, higher harmonics, voltage, current, torque, self-resonant frequency
Introduction
The main consumers of electricity on ships and sea-based objects are asynchronous electric drives. The use of energy-saving frequency-controlled asynchronous electric drives makes it possible to: reduce electricity consumption in shared modes by several times; expand the functionality of electrical equipment significantly. The structure of a modern frequency-controlled electric drive, which is optimal in terms of energy performance, control and mechanical characteristics, is based on a frequency converter with an intermediate DC link, which allows frequency control of the speed of asynchronous motors, in which the frequency and voltage of the motor supply can be changed in accordance with the established ratio independently from each other, for example, using the so-called control laws: U/f – the constancy of the magnetic flux, U2/f2 – the constancy of the critical moment, and so on. When these control laws are implemented, the speed of the induction motor changes in proportion to the frequency. By changing the frequency, smoothly and within a wide range, it is possible to adjust the speed of rotation of the rotor [1].
However, during operation, these electrical wires emit higher current harmonics into the supply network. An autonomous voltage inverter forms, along with the main series, higher harmonics of the output voltage supplied to the stator winding of an asynchronous electric motor. As you know [2, 3], higher voltage harmonics cause the corresponding higher harmonic currents flowing through the windings of an asynchronous motor, which leads to additional losses in the stator and rotor windings, the appearance of torques. The analysis of works in this area showed that the complex of problems that take place has not been studied enough and conducting theoretical, computational and experimental studies of higher harmonic components in the operation of frequency-controlled asynchronous electric drives is relevant.
Research materials and results
With the advent of static semiconductor frequency converters based on IGBT transistors, frequency-controlled electric drives were created, which are based on a frequency converter and an asynchronous motor (AM). Optimum in terms of energy performance, control and mechanical characteristics, the structure of a modern frequency-controlled asynchronous electric drive is based on a frequency converter with an intermediate DC link and consists of a rectifier (R) with an inductive-capacitive constant-voltage filter (CVF), a frequency converter control device (FCCD) and an autonomous voltage inverter (AVI) that forms the fundamental harmonic of the output voltage by pulse-width modulation [4] (Fig. 1). The efficiency of the rectifier with an inductive-capacitive constant voltage filter is up to 97% [4].
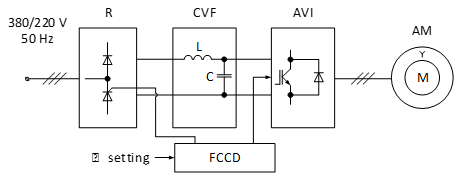
Fig. 1. Block scheme of a frequency-controlled electric drive
The mode of operation of the AM and its energy characteristics, as a rule, are analyzed under the conditions that the main harmonic of the voltage is supplied to the stator terminals at different frequencies and voltages. Theoretical, computational and experimental studies of higher harmonics that occur during the operation of frequency-controlled electric drives using a laboratory setup (Fig. 2) based on an AIR63V4 motor (Table 1) [5] were carried out.
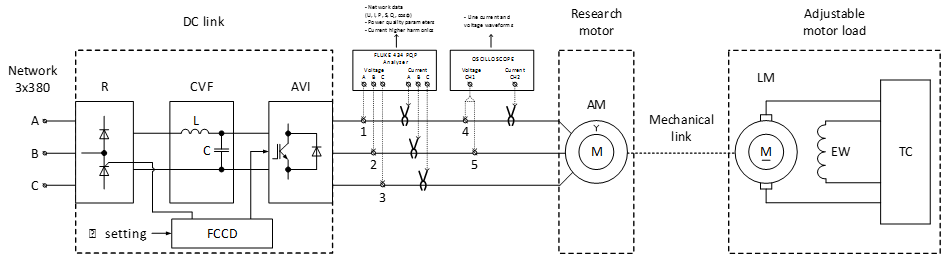
Fig. 2. Functional diagram for the study of a frequency-controlled electric drive when measuring parameters
at the input of an asynchronous motor
Table 1
Technical parameters of the asynchronous motor type 4AA63V4, similar to AIR63V4
|
Type |
Pnom, kW |
Unom, V |
Inom, A |
nsynch, rpm |
snom, % |
Istart/Inom |
Мmax/Mnom |
Мnom, N·m |
ΔPmech, W |
|
4АА63V4 |
0.37 |
380 |
1.2 |
1500 |
9 |
5 |
2.2 |
1.4 |
11 |
To carry out measurements at the AM input (Fig. 3, Table 2-4), the following were used: a FLUKE-434 power quality indicator meter, a two-beam oscilloscope connected from the side of the supply voltage (Fig. 2).
Table 2
Measurement results at the asynchronous motor input
|
I1, А |
UAB, V |
UAN, V |
P1, W |
Q1, VAr |
S1, VA |
|
0.72 |
400 |
231 |
232 |
503 |
554 |
The harmonic components of the input current and voltage are expanded in a Fourier series and are presented in Tables 3 and 4. THDI, THDU – the total coefficients of harmonic components of current, voltage at the point of transmission of electrical energy, % [6]:
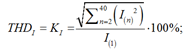

where I(n), U(n) – the amplitude values of the nth harmonic of current and voltage, respectively; I(1), U(1) – the amplitude values of the first harmonic of current and voltage, respectively.
The use of relatively powerful frequency converters can lead to distortion of the sinusoid of the supply voltage, since the higher harmonics of the current, propagating through the electrical network, create the corresponding voltage drops on its elements:
![]()
where zn – the resistance of the circuit section at the frequency of the nth harmonic; unetwork – network voltage.
The results of studies of the current and voltage at the AM input according to the scheme shown in Fig. 2 are given below (Fig. 4, Tables 5, 6).
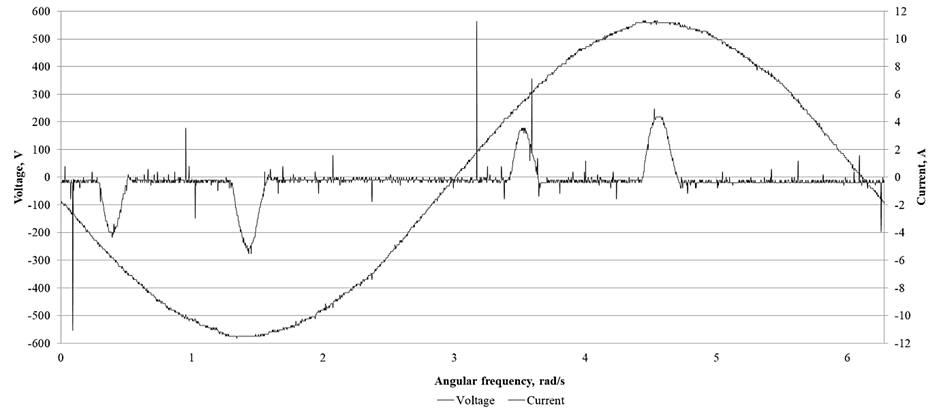
Fig. 3. Waveforms of the network current and voltage with power on the shaft of the asynchronous motor = 0.5Pnom
Table 3
Current harmonic composition from the side of the three-phase network 3 × 380 V
|
Phase |
THDI, % |
H3, % |
H5, % |
H7, % |
H9, % |
H11, % |
H13, % |
H15, % |
|
А |
183.5 |
25.5 |
95.1 |
98.0 |
19.6 |
81.4 |
83.5 |
16.3 |
|
B |
185.4 |
29.8 |
95.8 |
95.7 |
21.6 |
82.6 |
86.1 |
15.3 |
|
C |
172.2 |
20.6 |
91.06 |
89.5 |
14.8 |
77.1 |
79.8 |
13.9 |
Table 4
Voltage harmonic composition from the three-phase network 3 × 380 V
|
Phases |
THDU, % |
H3, % |
H5, % |
H7, % |
H9, % |
H11, % |
H13, % |
H15, % |
|
АB |
1.03 |
0.24 |
0.48 |
0.61 |
0.1 |
0.33 |
0.28 |
0.08 |
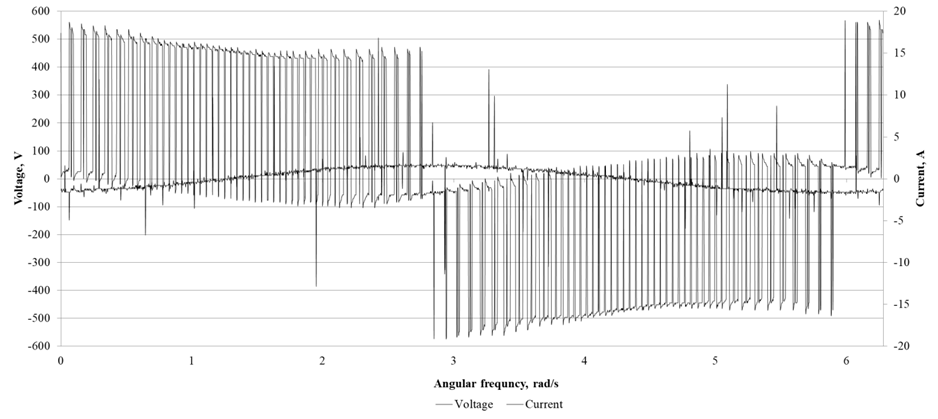
Fig. 4. Current and voltage waveforms at the input of the asynchronous motor
Table 5
Current harmonic composition at the input of the asynchronous motor
|
Phase |
THDI, % |
H3, % |
H5, % |
H7, % |
H9, % |
H11, % |
H13, % |
H15, % |
|
А |
29.7 |
0.2 |
23.0 |
11.1 |
0.3 |
9.1 |
6.1 |
0.1 |
|
B |
29.3 |
0.6 |
22.5 |
11.3 |
0.6 |
8.9 |
6.4 |
0.1 |
|
C |
29.8 |
0.5 |
23.3 |
10.7 |
0.4 |
9.4 |
6.0 |
0.6 |
Table 6
Voltage harmonic composition at the input of the asynchronous motor
|
Phases |
THDU, % |
H3, % |
H5, % |
H7, % |
H9, % |
H11, % |
H13, % |
H15, % |
|
АB |
3.3 |
0.8 |
1.4 |
2.3 |
0.7 |
1.2 |
0.6 |
0.3 |
The influence of higher harmonics on AM is manifested in additional heating of the windings, insulation aging, the occurrence of braking torques, vibration [2, 3].
Additional losses in AM caused by currents of the nth harmonic [1]:
![]()
where r1.n, r2.n' – respectively, the active resistances of the stator and rotor windings at the frequency of the nth harmonic.
At elevated frequencies, a surface effect appears in the stator and rotor windings of the electric motor [2]:
![]()
There is a significant spectrum of field harmonics in the air gap of the AM. The torques due to the higher harmonics, acting on the AM rotor, are additional. These include: asynchronous, synchronous, hysteresis and reactive torques [2]. The asynchronous torques of the 5th and 7th harmonics have the greatest influence on the AM from the torques under consideration, as the largest in terms of magnitude and nature of the impact. They respectively create torques of reverse and positive sequences. To calculate these torques, one should know the parameters of the equivalent circuit of an asynchronous motor (Fig. 5), which is similar to the equivalent circuit for the fundamental frequency, with the replacement of its parameters for the frequencies of higher harmonics [7].

Fig. 5. Equivalent circuit of an asynchronous motor
for higher harmonics
The torque of the nth harmonic reduced to the fundamental frequency in relative units [2]:
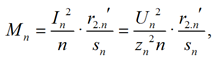
where Un – the voltage of the nth harmonic.
The slip for the nth harmonic is defined as follows [2, 3]:
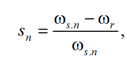
where ωs.n – the synchronous angular velocity of rotation of the nth harmonic; ωr – the angular speed of the motor rotor in the nominal mode.
The dependence of the moments of the fundamental, 5th and 7th harmonics on the angular velocity is shown in Fig. 6.
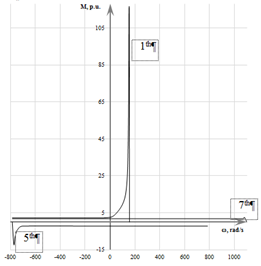
Fig. 6. Dependences of the torques of the first,
fifth and seventh harmonics on the angular velocity
of the rotor of the considered motor
Values of the moments for the 5th and 7th harmonics are increased by 100 times for the clarity of the characteristics. Since the value of the slip of the rotor for the currents of all harmonics is almost the same, the relative torques are small, thus their influence on the average torque is insignificant. However, this leads to the appearance of vibrations of the motor shaft at a frequency of 300 Hz from the interaction of the moments of the 5th and 7th harmonics [2]. Accordingly, there is vibration at a frequency of 600 Hz from the interaction of the moments of the 11th and 13th harmonics [2]. Vibration at a frequency of 50 Hz is due to the influence of the fundamental harmonic.
Measurement of the frequency spectrum of AM axial vibration signals (fX, fY, fZ) by means of an accelerometer is shown in Fig. 7.
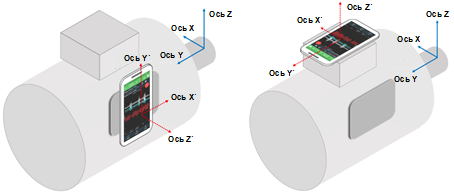
Fig. 7. Scheme of the experimental setup for measuring
the frequency spectrum of signals of axial vibrations
of the asynchronous electric motor
Figures 8, 9 show the results of measurements taken from the accelerometer along the X axis for various frequency ranges.
The main vibration parameters measured to assess the technical condition of dynamic machines in accordance with GOST ISO 10816-1 [8] are vibration velocity, vibration displacement and vibration acceleration, m/s2, or g – free fall acceleration.
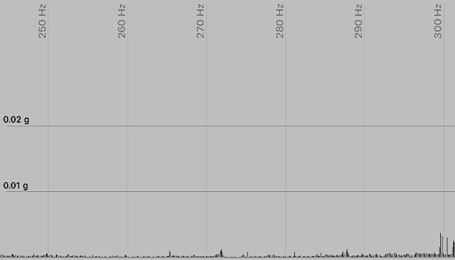
Fig. 8. Vibration signal of the asynchronous motor
from 250 to 300 Hz at the nominal speed of rotation
of the rotor and the load on the motor shaft along the X axis
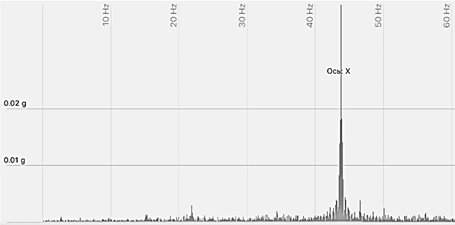
Fig. 9. Vibration signal of the asynchronous motor
from 0 to 60 Hz at the nominal speed of rotor rotation
and the load on the motor shaft along the X axis
During operation of the laboratory setup, vibration occurs at a frequency of 300 Hz (Fig. 8).
At the design stage of an electric drive, it is important to know its self-resonant frequency in order to avoid resonance at a frequency of 50, 300, 600 Hz and so on. The method for calculating the natural frequency of oscillations of the investigated electric drive is described below.
Two shafts connected by an elastic coupling represent an oscillatory system with two degrees of freedom (Fig. 10).

Fig. 10. Oscillating electric drive system (an asynchronous motor, a coupling, a DC motor)
The frequency equation for this system has the form [9]:
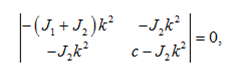 (1)
(1)
where J1 – the moment of inertia of the AM rotor; J2 – the moment of inertia of the DC motor armature (DC motor); c – the torsional stiffness coefficient.
For a cylindrical elastic element (coupling), the torsional stiffness coefficient is [9]:

where G – the elastic modulus of the second kind of rubber equal to 5 MPa; L – the length of the cylindrical coupling; J0 – polar moment of inertia, J0 = πD4 / 32; D – the diameter of the cylindrical coupling.
At D = 56 mm, L = 10 mm, the torsional stiffness coefficient of the coupling is c = 482.5 N·m.
Two oscillation frequencies [9]:
k1 = 0;
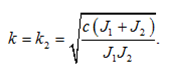 (2)
(2)
One frequency, k = k2, turned out to be nonzero. The factors leading to damping of oscillations were neglected. To determine the natural oscillation frequency of the system using formula (1), it is necessary to calculate the moments of inertia J1 and J2 of the AM rotor and the DC motor armature, respectively. For simplicity, we will present all the configuration elements of the movable and fixed parts of the AM and DC motor in the form of cylindrical bodies (Fig. 10). Then the moment of inertia of the shaft of the AM-DC motor system will be equal to the sum of the moments of inertia of these cylindrical bodies. The moment of inertia of a solid homogeneous cylinder is [9]:
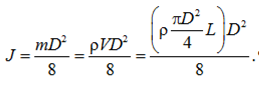
Then the total moment of inertia of the AM rotor J1 is equal to 1.6 · 10–3 kg·m2. To estimate the moment of inertia of the DC motor armature, it was considered that this is a cylindrical body (Fig. 10), consisting of half of copper, half of steel (ρ1 = 8 930 kg/m3 and ρ2 = 7 800 kg/m3, respectively). Then the total moment of inertia of the DC motor armature J2 is equal to 54.5 · 10–3 kg·m2 [9].
Evaluation of the self-resonant frequency of the oscillatory system by formula (2) gives the result k = 557 Hz. For an accurate calculation of the self-resonant frequency of the oscillatory system, it is necessary to experimentally measure the moments of inertia of the AM rotor and the DC motor armature.
Conclusion
As part of the research, the following results were obtained:
1. During the operation of ship frequency-controlled asynchronous electric drives, higher current harmonics are emitted to the supply network, mainly 5, 7, 11, 13 orders, due to the presence of a six-phase rectifier. This leads to a distortion of the sinusoid of the supply voltage, since the higher harmonics of the current, propagating through the electrical network, create the corresponding voltage drops on its elements.
2. Along with the main voltage harmonic of a given frequency, higher harmonic voltages are supplied to the stator winding of an asynchronous electric motor from an autonomous voltage inverter. As a result, there is heating of the windings, moments of reverse and positive sequences, leading to machine vibration.
3. A technique has been developed and the vibration of a machine at a frequency of 300 Hz from the interaction of the moments of the fifth (reverse sequence) and seventh (positive sequence) harmonics has been experimentally confirmed.
4. A method for calculating the self-resonant frequency of oscillations of the electric drive is proposed, confirmed by the example of a laboratory installation.
1. Romanenko N. G., Golovko S. V., Zhumanazarov M. P. Issledovanie svoistv preobrazovatelia chastoty v kachestve istochnika pitaniia sudovogo elektrooborudovaniia [Investigation of the properties of a frequency converter as a power source for marine electrical equipment]. Vestnik Astrakhanskogo gosudarstvennogo tekhnicheskogo universiteta. Seriia: Morskaia tekhnika i tekhnologiia, 2017, no. 1, pp. 76-81.
2. Arrillaga J., Bradley D. A., Bodger P. S. Power system harmonics. Chichester etc.: Wiley, 1985. 336 p. (Arrillaga Dzh., Bredli D., Brodzher P. Garmoniki v elektricheskikh sistemakh / per. s angl. E. A. Vasil'chikova. M.: Ener-goatomizdat, 1990. 320 s.).
3. Kopylov I. P. Elektricheskie mashiny [Electric machines]. Moscow, Logos Publ., 2000. 607 p.
4. Shabalin L. D., Chushankov D. Iu. Obosnovanie modernizatsii sudovykh elektroprivodov gruzopod"emnykh ustroistv na sistemy s ispol'zovaniem preobrazovatelei [Justification of modernization of marine electric drives of lifting devices for systems using converters]. Izvestiia Kaliningradskogo gosudarstvennogo tekhnicheskogo universiteta, 2016, no. 42, pp. 213-222.
5. Kravchik A. E., Shlaf M. M., Afonin V. I. i dr. Asinkhronnye dvigateli serii 4A: spravochnik [Asynchronous motors of the 4A series: reference]. Moscow, Energoatomizdat, 1982. 380 p.
6. Zhezhelenko I. V. Vysshie garmoniki v sistemakh elektrosnabzheniia prompredpriiatiia [Higher harmonics in industrial power supply systems]. Moscow, Energoatomizdat, 1974. 160 p.
7. Kostic M. Equivalent circuit and induction motor parameters for harmonic studies in power networks. Research Gate, 2012. Available at: https://www.researchgate.net/publication/259339771_Equivalent_Circuit_and_Induction_Motor_Parameters_for_Harmonics_Studies_in_Power_Networks (accessed: 13.04.2023).
8. GOST ISO 10816-1-97. Vibratsiia. Kontrol' sostoianiia mashin po rezul'tatam izmerenii vibratsii na nevrashchaiushchikhsia chastiakh. Part 1. Obshchie trebovaniia [Vibration. Monitoring the condition of machines based on the results of vibration measurements on non-rotating parts. Part 1. General requirements]. Moscow, Standartinform Publ., 2014. 18 p.
9. Vul'fson I. I. Kratkii kurs teorii mekhanicheskikh kolebanii [A short course in the mechanical vibrations theory]. Moscow, VNTR Publ., 2017. 241 p.