Omsk, Russian Federation
Russian Federation
In digital signal processing the question of the speed of the algorithms speed used is becoming more and more relevant. The convolution and correlation operations used are most often based on standard function libraries, which are focused on reducing data processing time by splitting the source data into sections. With small amounts of data, these algorithms work quite efficiently. However, in practice, with a significant increase in the dimension of the input data, the methods lose quite a lot in the speed of data processing. A method for calculating the convolution of large signals based on the practical performance of the fast Fourier transform is proposed. The optimal size of the section is analyzed, in which the practical performance of existing algorithms remained at a sufficiently high level. Based on the experimental calculations carried out, the optimal dimension of the section used in the convolution calculation formulas was chosen. The proposed method has been tested on published data from various studies. The significant advantages of the proposed method in solving a number of problems are the reduction of the convolution calculation time for long signals by tens of percent and the possibility of fine-tuning the method for specific computing platforms when using preliminary run-time testing on a fast Fourier transform platform of various sizes
fast Fourier transform, section, sectional convolution method, correlation, signal, performance, speed
Введение
Задача выполнения операции свертки, вместе со схожей по математическому описанию корреляцией, широко используется при цифровой обработке сигналов [1], обработке больших данных и в задачах искусственного интеллекта [2]. Свертка является базовой операцией при определении результата взаимодействия сигнала с некоторой системой, а корреляция является одним из лучших способов для сравнения сигналов.
Современное развитие средств вычислительной техники расширило круг задач, которые можно решать в указанных областях применения рассматриваемых операций, и привело к увеличению размера обрабатываемых сигналов и наборов данных. При этом возникают задачи, для решения которых требуется выполнить свертку или вычислить корреляцию для последовательностей, содержащих несколько тысяч или даже миллионов отсчетов.
Для выполнения операций свертки и корреляции с последовательностями больших размеров были предложены способы сокращения времени выполнения этих операций за счет уменьшения числа арифметических операций, требуемых для их выполнения. Часть этих способов использует идеи, аналогичные идеям, заложенным в алгоритм умножения Карацубы [3]: разложение последовательностей на последовательности меньшей длины, выполнение операций над последовательностями меньшей длины и объединение результатов. Другая часть способов использует перевод последовательностей в спектральную область с помощью быстрого преобразования Фурье (БПФ), выполнение операции в спектральной области и восстановление результата с помощью обратного преобразования Фурье [4]. Группа алгоритмов, называемых секционной сверткой, для достижения наилучшего результата комбинирует два описанных выше способа [5].
В достаточно типичном случае, когда одна из последовательностей имеет очень большую длину (порядка 215 или более отсчетов), наибольшее быстродействие показывает алгоритм секционной свертки. Этот алгоритм имеет ряд вариаций и параметров, из которых одним из важнейших является размер секции – длина подпоследовательностей, на которые разбивается большая из последовательностей.
Оптимальный размер секции может быть вычислен теоретически, исходя из известных формул для расчета количества операций алгоритмов, используемых алгоритмом секционной свертки. Многие практические реализации свертки и корреляции используют такую формулу расчета размера секции
(с некоторой корректировкой результата). Вместе с тем следует отметить, что для многих вычислительных задач теоретическая и практическая оценки быстродействия могут существенно отличаться.
В текущей работе исследуется вопрос выбора размера секции секционной свертки с целью уменьшения времени работы практических реализаций этого алгоритма.
Состояние проблемы
Для краткости и простоты изложения далее будем использовать терминологию из области цифровой обработки сигналов. В частности, вместо математического термина «числовая последовательность» будет применяться понятие «сигнал».
Пусть заданы два сигнала ![]() и
и ![]() , где N, М – количество элементов последовательностей.
, где N, М – количество элементов последовательностей.
Линейная свертка сигналов будет определяться по формуле (здесь и далее подразумевается, что значение сигналов за границами заданных индексов равно нулю) [6]
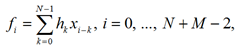
где k, i – индексы отсчетов соответствующих сигналов.
Если не указано иное, далее под сверткой будем понимать линейную свертку.
Взаимная корреляция (корреляция) двух сигналов рассчитывается по формуле [6]
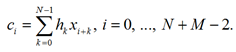
С вычислительной точки зрения обе эти операции выполняются с помощью одних и тех же арифметических действий, фактически свертка – это корреляция с развернутым в обратном порядке сигналом, и наоборот. Ввиду сказанного с точки зрения проблемы увеличения быстродействия эти операции абсолютно одинаковы.
Следует отметить, что при практическом применении для корреляции обычно необходимо рассчитывать только те отсчеты выходного сигнала, которые содержат полную сумму из ненулевых элементов, а свертка может применяться в различных вариантах, отличающихся длиной выходных сигналов. Но это замечание несущественно влияет на целесообразность совместного рассмотрения операции свертки и корреляции с точки зрения практической реализации.
Для вычисления свертки или корреляции (далее будем говорить только о свертке, подразумевая, что сказанное применимо и к корреляции) требуется выполнить количество арифметических операций, пропорциональное произведению длин входных сигналов, или, другими словами, сложность этих операций равна O(N · M). Для сигналов с большой длиной количество операций может стать неприемлемо большим.
Одним из методов сокращения числа арифметических операций при вычислении свертки является сведение ее к циклической свертке и вычисление циклической свертки через БПФ [7].
Циклическая свертка вычисляется по формуле
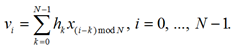
Для преобразования линейной свертки в циклическую последовательности h и x дополняются нулями до некоторого L = N + M – 1, после чего вычисляется циклическая свертка дополненных последовательностей, результаты которой будут совпадать с линейной сверткой.
Циклическая свертка может быть быстро вычислена с помощью БПФ по следующей формуле [8]:
![]()
где FFT – оператор БПФ; IFFT – оператор обратного БПФ, а произведение внутри формулы – это поэлементное произведение векторов.
Сложность вычисления по этой формуле будет равна сложности БПФ, т. е. O(L · log(L)). Такой способ вычисления свертки сигналов при больших
и примерно равных значениях N и M будет давать существенное сокращение числа арифметических операций.
Достаточно часто встречается ситуация, когда только один из сигналов имеет большую длину. Например, при фильтрации цифровых сигналов ядро фильтра имеет ограниченную длину, а сам сигнал практически бесконечен. Если длина меньшего из сигналов сопоставима с логарифмом от длины большего сигнала, вычисление свертки через БПФ будет требовать большего числа арифметических операций, чем прямое вычисление по формуле из определения.
Для рассмотренного в последнем абзаце случая был предложен метод вычисления, который называется секционная свертка. Идея этого метода заключается в разбиении более длинного сигнала на секции, вычисление свертки меньшего сигнала с каждой из секций, а затем объединение результатов. Размер секций выбирается таким образом, чтобы свертка с секцией могла быть эффективно вычислена с помощью БПФ.
В рамках метода секционной свертки можно выделить несколько методов, отличающихся между собой способом объединения секций.
В методе перекрытия с суммированием более длинный входной сигнал разбивается на непересекающиеся смежные секции длиной L. Каждая секция и короткий сигнал дополняются нулями до размера L + N – 1, где N – длина короткого сигнала. После выполнения прямого и обратного БПФ в каждой секции получается выходной сигнал длиной L + N – 1. Индексы выходных сигналов соседних секций перекрываются в N – 1 точке и должны быть просуммированы между собой.
В методе перекрытия с накоплением входной сигнал разбивается на пересекающиеся секции длиной L + N –1, сдвинутые друг относительно друга на L отсчетов. В этом случае от результата в каждой секции отбрасываются последние N – 1 отсчетов и в итоговый результат объединяются по L отсчетов из каждой секции.
Различные методы секционной свертки имеют свои особенности в плане удобства реализации и быстродействия, однако с точки зрения выбора размера величины L и размера БПФ они идентичны. Далее мы будем рассматривать метод перекрытия с суммированием, но все нижесказанное может быть применено и к методу перекрытия с накоплением.
Выведем формулу для оптимального размера секций, исходя из оценки количества арифметических операций, затрачиваемых на расчет одного отсчета выходного сигнала. Для удобства выкладок обозначим K = N – 1 и B = L – 1.
Общее количество операций для выполнения двух прямых и одного обратного преобразования Фурье будет пропорционально Blog(2B). Вычислительные затраты на умножение результатов БПФ и на объединение секций будут иметь меньший порядок, и ими можно пренебречь. По результатам обработки одной секции находится B – K отсчетов выходного сигнала. Таким образом, нам нужно минимизировать следующее соотношение:
![]()
На рис. 1 приведен пример графика минимизируемой функции для случая K = 100 отсчетов.
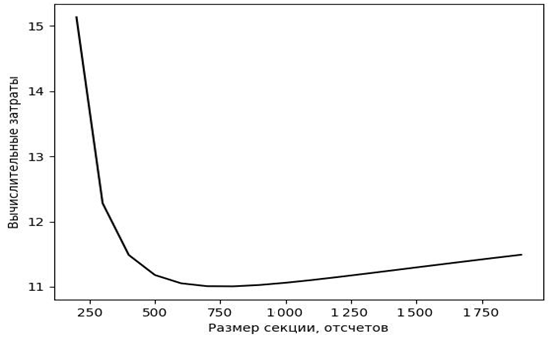
Рис. 1. Пример минимизируемой функции для K = 100
Fig. 1. Example of a minimized function for K = 100
На графике видно, что минимизируемая функция имеет минимум, после которого идет ее медленное нарастание. С точки зрения реализации секционной свертки это означает, что мы можем выбирать размер секции выше минимума на графике, исходя из наличия быстродействующей реализации БПФ соответствующего размера.
Значение B, минимизирующее величину C, можно получить, взяв производную и приравняв ее к нулю. Представим C в виде произведения
C1 = B / (B – K) и C2 = log(2B) = ln(2B) / ln(2). Вычислим производную произведения:
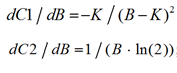
![]()
Приравняв производную нулю после преобразования, получим:
![]() .
.
Данное уравнение может быть решено сведением к виду ![]() , где W – функция Ламберта. Получаем следующую формулу для оптимального размера секции:
, где W – функция Ламберта. Получаем следующую формулу для оптимального размера секции:
![]() .
.
Данная формула применяется для выбора размера секции в различных библиотеках для научных вычислений, в частности в пакете signal библиотеки SciPy.
В результате экспериментальных исследований авторами статьи было установлено, что во многих случаях можно уменьшить время выполнения свертки, увеличив размер секции. Это говорит о том, что вопрос выбора оптимального размера секций для практических реализаций остается открытым и будет рассмотрен в данной статье. Результаты этих исследований мы не приводим, поскольку тезис из предыдущего предложения подтверждается приведенными ниже результатами исследований предлагаемого метода.
Предлагаемый метод
После теоретического и экспериментального изучения способа определения размера секции в методе секционной свертки было высказано предположение, что для получения большей скорости вычисления операции свертки нужно рассмотреть практическое быстродействие БПФ.
На рис. 2 представлен пример моделирования производительности двух реализаций БПФ из библиотеки SciPy (на графике – fft_sci) и NumPy (fft_num): на оси абсцисс отложен двоичный логарифм от количества отсчетов сигналов, участвующих в операции БПФ, по оси ординат – производительность БПФ; производительность БПФ показывает количество операций, выполняемых реализацией БПФ в единицы времени и измеряется в мегафлопсах (миллион операций с плавающей точкой в секунду).
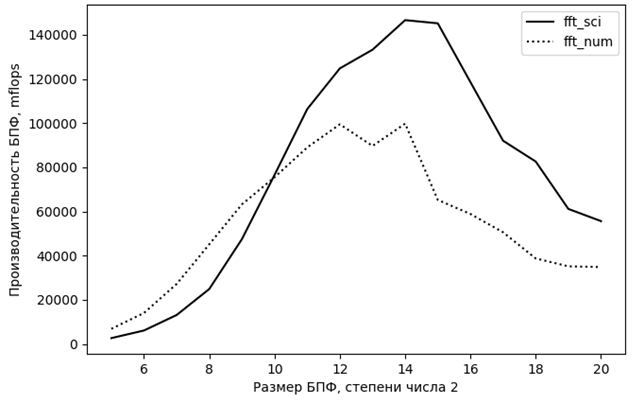
Рис. 2. Производительность БПФ для двух вариантов реализации
Fig. 2. FFT performance for two implementation options
Численно эта величина для комплексного преобразования определяется как [9]
![]() ,
,
а для вещественного как
![]() ,
,
где t – время выполнения одного преобразования БПФ в микросекундах.
График производительности БПФ возрастает до размера БПФ, примерно равного 212–214, после чего выходит на небольшое плато, после которого следует спад производительности. Результаты других исследований [10] подтверждают, что такой характер графика производительности характерен для различных реализаций БПФ и различных современных процессоров.
Анализируя параллельно рис. 1 и 2, можно отметить, что эффективность выполнения свертки слабо зависит от размера секции после точки минимума,
а производительность БПФ сильно зависит от связанного с размером секции размера БПФ. Таким образом, на общее быстродействие функции секционной свертки в большей степени влияет производительность БПФ для выбранного размера секции, и, следовательно, при выборе размера секции в первую очередь нужно учитывать этот параметр.
К сожалению, практическая производительность БПФ зависит от реализации БПФ и от устройства, на котором БПФ выполняется. Ввиду этого невозможно провести полноценную оптимизацию вычисления свертки, которая одинаково хорошо работала бы на всех устройствах, однако можно сократить среднее время вычисления, основываясь на усредненных данных различных графиков производительности БПФ.
Суть предлагаемого метода сводится к простому правилу: использовать в качестве размера секции усредненный размер БПФ с наибольшей производительностью, равный 213.
Отдельно следует оговорить случаи, при которых вместо секционной свертки более быстрым оказывается обычное вычисление свертки через БПФ. Проведенные экспериментальные исследования сравнительной производительности этих двух вариантов показали, что секционную свертку следует применять при размере наибольшего сигнала не менее 216. Подтверждение этого факта можно найти в приведенных ниже экспериментальных исследованиях предлагаемого метода, а также в опубликованных графиках других исследований [10].
Экспериментальное исследование
Для проведения экспериментальных исследований предлагаемого метода на языке Python была реализована функция conv_tune_fft, вычисляющая свертку двух сигналов. При вызове эта функция определяет размер наибольшего сигнала и, если он оказывается меньше 216, вызывает функцию fftconvolve из библиотеки SciPy и возвращает результат ее работы. В противном случае выполняется секционная свертка с размером секции, равным 213.
Были проведены эксперименты для различных длин наименьшего сигнала h. Результат экспериментов для h = 256 представлен на рис. 3, где по оси абсцисс отложен двоичный логарифм длины второго сигнала (количество отсчетов, соответствующих степени числа 2), а по оси ординат – среднее время вычисления свертки в микросекундах.
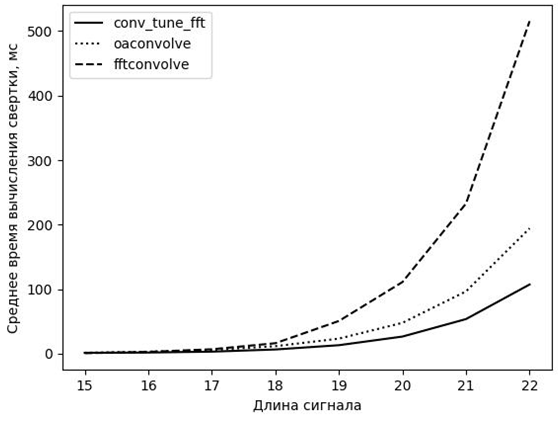
Рис. 3. Зависимость скорости вычисления свертки от длины сигнала
Fig. 3. Dependence of the convolution calculation speed on the signal length
Кроме уже упомянутых функций на рис. 3 также приведен график для времени работы функции oaconvolve из библиотеки SciPy, вычисляющей свертку секционным методом.
Как видно из рис. 3, предлагаемый метод позволяет заметно сократить время вычисления свертки. При длине сигнала 222 время вычислений сократилось на 70 % по сравнению со стандартной реализацией секционной свертки, и можно ожидать еще большего выигрыша при большей длине сигнала.
При расчетах свертки для сигналов с другими размерами h, и при запуске экспериментов на компьютерах с процессорами различной архитектуры были получены аналогичные результаты, во всех случаях conv_tune_fft оказывалась быстрее.
Заключение
Предлагаемый метод реализации секционной свертки позволяет сократить время вычисления свертки для длинных сигналов на десятки процентов, что является существенным преимуществом при решении ряда задач.
Используя изложенное в статье описание факторов, влияющих на быстродействие метода секционной свертки, можно проводить тонкую настройку этого метода для конкретных вычислительных платформ, используя предварительное тестирование времени выполнения на платформе БПФ различных размеров.
Предложенный подход с оценкой практического быстродействия БПФ может быть использован для оптимизации других алгоритмов цифровой обработки сигналов, построенных на основе БПФ.
Одним из перспективных направлений для применения этого подхода является его использование при реализации многомерной свертки или корреляции.
1. Sergienko A. B. Tsifrovaia obrabotka signalov: uchebnik dlia vuzov [Digital signal processing: textbook for universities]. Saint-Petersburg, Piter Publ., 2002. 608 p.
2. Ob"iasnimyi iskusstvennyi intellekt [Explicable artificial intelligence]. Nauchno-tekhnicheskii tsentr FGUP «GRChTs». Available at: https://rdc.grfc.ru/2020/12/explainable-ai/ (accessed: 20.04.2023).
3. Okulov S. M., Lialin A. V., Pestov O. A., Razova E. V. Algoritmy komp'iuternoi arifmetiki [Algorithms of computer arithmetic]. Moscow, Laboratoriia znanii Publ., 2015. 285 p.
4. Shtokalo I. Z. Operatsionnoe ischislenie (obobshcheniia i prilozheniia) [Operational calculus (generalizations and applications)]. Kiev, Naukova dumka Publ., 1972. 304 p.
5. Gould B., Rabiner L. Teoriia i primenenie tsifrovoi obrabotki signalov [Theory and application of digital signal processing]. Moscow, Mir Publ., 1978. 848 p.
6. Emmanuil C. A., Barri U. D. Tsifrovaia obrabotka signalov: prakticheskii podkhod [Digital signal processing: a practical approach]. Moscow, Vil'iams Publ., 2004. 992 p.
7. Bleikhut R. Teoriia i praktika kodov, kontroli-ruiushchikh oshibki [Theory and practice of error-controlling codes]. Moscow, Mir Publ., 1986. 576 p.
8. Lineinaia i tsiklicheskaia svertka [Linear and cyclic convolution]. DSPLIB.org. Available at: https://ru.dsplib.org/content/conv/conv.html (accessed: 07.04.2023).
9. FFT Benchmark Methodology. FFTW. Available at: https://fftw.org/speed/method.html (accessed: 07.04.2023).
10. benchFFT. FFTW. Available at: https://fftw.org/benchfft/ (accessed: 07.04.2023).















