Russian Federation
The article describes modeling the spread of impurities in a continuous medium using the oil leak from a pipeline laid along the bottom of a reservoir as an example, based on the software developed using supercomputer technologies in the C language. A mathematical model is proposed that describes the process of impurity transport in the aquatic environment. The problem is reduced to solving a system of two equations: a generalized differential equation for the transfer of impurities and an equation for the velocity field. In the generalized equation for the transport of impurities, the variable from the function can be expressed by different parameters; within the framework of this problem, the variable is a concentration. In the simulated situation, oil products leak from the main pipeline, the oil products continuously flow into the water source. For the study, there was simulated the area with given boundaries and initial parameters: the size of the area, the flow velocity and the density of the medium. The process of developing and testing a software package based on OpenMP-CUDA is presented. The functionality of the created program allows you to predict the speed and range of propagation of various impurities in various environments with a visual representation. The software package consists of two modules: calculation and visualization. The calculation module is implemented by transferring the computational load to the video card. The graphics module is implemented in Python using the Matplotlib library. The results of numerical simulation of the propagation of a pollutant in a continuous medium are presented. The result obtained coincides with a coincidence with the real situation and the results of other studies. With increasing amount of experimental data and dependent variables (ambient temperature, water salinity, etc.), the accuracy of modeling will increase. The analysis of oil leakage at different fistulas was made in case of an accident and comparison with the results of computer simulation.
impurity transport, software package, mathematical model, numerical simulation, pipeline, leak formula, OpenMP, CUDA, graphics accelerator, oil outflow
Введение
В настоящее время случаи загрязнения окружающей среды нефтепродуктами приводят к негативным последствиям для экологии, разрушающий масштаб которых невозможно предугадать. Согласно исследованиям [1, 2], за последние 20 лет наибольшая доля в загрязнении среды продуктами нефти приходится на транспортировку. На рис. 1 представлена диаграмма источников загрязнения нефтью окружающей среды.
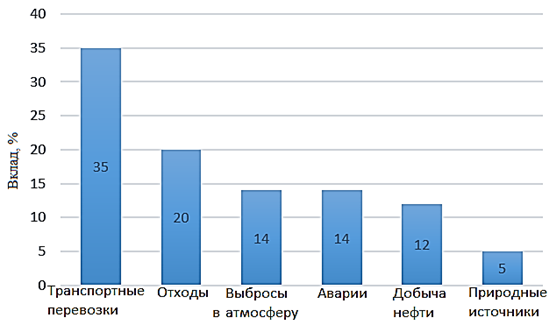
Рис. 1. Доля различных источников в загрязнении окружающей среды нефтью
Fig. 1. Share of different sources in oil pollution
В данной ситуации особенно важную роль играют получение объективной информация о критических показателях антропогенного воздействия,
о фактическом состоянии гидросферы и составление прогнозов ее будущего состояния при различных авариях. В решении этих задач может помочь разработанный программный комплекс для моделирования распространения примесей в сплошной среде. За его основу взят разработанный ранее программный комплекс для моделирования распространения переноса примесей в приземленном слое атмосферы [3], который реализуется с помощью слияния технологий параллельного программирования OpenMP и CUDA. Разработанное программное обеспечение (ПО) может служить для прогнозирования распространения различных примесей в сплошной среде, а распараллеливание и перенос расчетов на графический ускоритель значительно сокращает время моделирования.
Постановка цели и задачи исследования
Целью исследования является моделирование процесса переноса примеси в сплошной среде, которое реализовано разработанным ПО с использованием суперкомпьютерных технологий CUDA и OpenMP.
Для достижения поставленной цели требуется решить следующие основные задачи:
1. Построить математическую модель процесса переноса примесей, протекающих в сплошной среде.
2. Реализовать численное решение для программного комплекса.
3. Реализовать ПО для компьютерного моделирования с использованием программно-аппаратных архитектур параллельных вычислений OpenMP
и CUDA.
4. Провести тестирование ПО и верификацию компьютерной модели, основываясь на известных исследованиях.
Конечным результатом исследования является новый программный комплекс для численного моделирования переноса загрязняющей примеси
в сплошной среде. Разработанное ПО предназначено для моделирования и прогнозирования распространения примеси в заданной области.
Математическая модель для программного комплекса
В работе моделируется заданное пространство водной среды с заданной скоростью течения. В моделируемой ситуации поврежденный трубопровод проложен по дну рассматриваемой области [4].
За основу математической модели взято обобщенное дифференциальное уравнение переноса примесей, которое имеет вид

где t – время моделирования; ρ – плотность среды; Ф – обобщенная переменная; xi – пространственная координата; ui – компонент скорости в направлении xi; Dп – коэффициент переноса массы; S – источник загрязнения.
Рассмотрим систему дифференциальных уравнений [5, 6]:
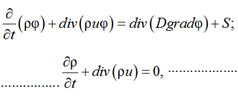 (1)
(1)
(2)
где φ – концентрация примеси; u – скорость течения; D – коэффициент диффузии.
Компоненты вектора скорости распространения примеси определяются уравнением состояния и зависят от нескольких параметров: температуры среды, концентрации примеси, уравнения неразрывности, закона сохранения массы [5].
В декартовой системе координат уравнение (1) и уравнение поля скорости (2) запишутся следующим образом:
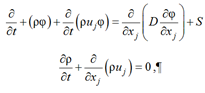 ,
,
где индекс j соответствует пространственным координатам x, y, z. В настоящей работе рассматривается только двумерный случай, поэтому координата z не учитывалась. Уравнения ниже представлены в общем виде:

Реализация численного моделирования
Для численного моделирования использовался разработанный программный комплекс, написанный на языке С, за основу которого взята программа, созданная для численного моделирования переноса примесей в атмосфере и описанная в предыдущей работе [3]. Алгоритм ПО строится на основе программно-аппаратной архитектуры CUDA и распараллеливания программы с помощью OpenMP [3]. На рис. 2 представлена диаграмма, отражающая потоки данных и передачу управления между функциональными частями разработанной программы, распараллеленная на 2 графических ускорителя.

Рис. 2. Диаграмма потоков для двух графических ускорителей
Fig. 2. Graph of flows for two graphics accelerators
Расчетная часть программы выполняется параллельно на нескольких OpenMP потоках. В каждом из них обрабатывается собственная часть расчетной области на отдельном графическом ускорителе.
Такая архитектура удобна и легко масштабируема для большого числа сопроцессоров, что позволяет проводить численное моделирование больших расчетных областей с высокой разрешающей способностью. Для синхронизации работы потоков использована технология объединенной памяти (UnifiedMemory), которая образует общее адресное пространство для переменных как на центральном процессоре, так и на всех графических картах.
Однако следует отметить недостаток такого подхода, выраженный в невысокой переносимости, т. к. технология объединенной памяти поддерживается не всеми GPU.
Основная вычислительная нагрузка алгоритма выполняется на графических ускорителях. Первым этапом запускается cuda-ядро для основных вычислений. Значение этих величин для каждого расчетного узла вычисляется на отдельном cuda-потоке.
Вторым этапом происходит переход на следующий временной слой. Процедура интегрирования выполняется схемой предиктор-корректор.
Далее управление передается на CPU, где выполняется шаг по времени. Также при необходимости происходит выгрузка промежуточных данных.
В рамках работы принято решение об использовании только одного графического ускорителя в расчетной части программы. Это объясняется тем, что моделируемая область была небольшой, поэтому отсутствует необходимость разделять ее на части, как в предыдущих работах. Основные расчеты происходят на одной видеокарте, смена итерации на центральном процессоре, демонстрируя распараллеливание OpenMP. На рис. 3 представлена диаграмма потоков для разработанной программы с одной видеокартой.
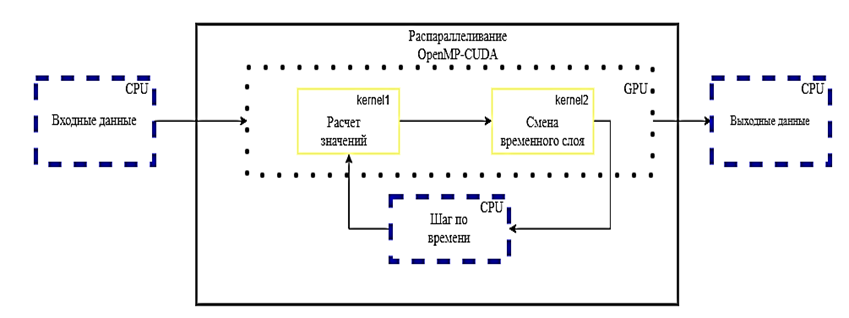
Рис. 3. Диаграмма потоков для одного графического ускорителя
Fig. 3. Graph of flows for one graphics accelerator
Для задачи выбраны следующие параметры области моделирования:
– размер расчетной области – 5 × 5 м;
– пространственное разрешение – 0,05 м;
– плотность среды – 1 000 кг/м3;
– скорость течения – 1 м/с.
На рис. 4 представлена область моделируемого водоема.
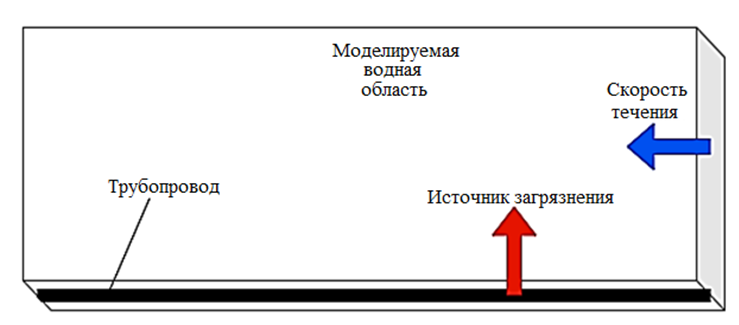
Рис. 4. Моделируемая область загрязнения нефтью
Fig. 4. Modeled area of oil pollution
У заданного источника загрязнения следующие параметры: плотность нефти составляет 800 кг/м3, концентрация задана единицей. Это означает, что значения концентрации в ячейках расчетной области распределяются от 0 до 1.
Визуализация распределения концентрации примеси реализована графическим модулем, написанным на языке Python. По завершении работы расчетного модуля программы формируется файл, отражающий значения концентрации примеси в ячейках, который передается в модуль визуализации и реализуется с помощью библиотеки matplotlib.
Общее время моделирования составляло 5 с. Результаты моделирования в разные моменты времени распространения нефти при аварии трубопровода представлены на рис. 5, 6, на которых демонстрируются пространственные распределения нефтяной примеси (по горизонтальной и вертикальной осям откладываются соответствующие пространственные координаты, м)).

|
Рис. 5. Распределение концентрации примеси в начальный период времени: t = 2 c (а); t = 3 c (б)
Fig. 5. Distribution of impurity concentration in the initial period of time: t = 2 s (а); t = 3 s (б) |

Рис. 6. Распределение концентрации примеси в конечный момент времени: t = 4 c (а); t = 5 c (б)
Fig. 6. Distribution of impurity concentration at the final moment of time: t = 4 s (а); t = 5 s (б)
Наибольшая концентрация нефти сосредоточена в начальный момент времени в месте разрыва трубы. Сначала нефть из-за разницы плотностей стремится наружу (вверх), но ее «сносит» по направлению течения с уменьшением концентрации у очага [4].
На рис. 6 концентрация у очага минимальна в связи с тем, что примесь «размывается» и нефть перестает транспортироваться после аварии.
На основе моделирования можно сделать вывод о качественном совпадении результатов численного эксперимента с данными, представленными другими исследователями. Однако для подтверждения адекватности реализации численной схемы необходимо в дальнейшем провести количественный анализ результатов увеличения моделируемой области [7, 8].
Также для будущих работ проведен эксперимент с различным диаметром отверстия для истечения [4]. Для расчета количества нефти, которая утекла, использовалась классическая формула утечки
![]() (3)
(3)
где Q – массовый расход нефти; C0 – коэффициент истечения (рекомендуется 0,61); A – площадь скважины; ρ – плотность среды; Pl – фактическое давление в трубопроводе; Ps – давление среды.
На рис. 7 приведен график изменения скорости истечения нефти в зависимости от диаметра отверстия, вычисленного по формуле и путем компьютерного моделирования.

Рис. 7. Скорость выделения нефти при разном диаметре отверстий
Fig. 7. Oil release rate at different hole diameters
Скорость истечения, рассчитанная по формуле (3), выше, чем при моделировании, и разница в значениях увеличивается с увеличением диаметра отверстия.
Полученные выводы совпадают с результатами других исследователей [4] и прошлыми работами [3, 7]. Погрешность может быть вызвана недостаточным количеством учитываемых параметров в модели. Полученные первичные результаты моделирования можно использовать для прогнозирования аварий
и, соответственно, для их предотвращения.
Заключение
Представлены результаты работы программного комплекса, разработанного на основе скрещивания технологии распараллеливания потоков OpenMP
и программно-аппаратной архитектуры CUDA для численного моделирования динамики переноса примесей в сплошной среде. Использование графического процессора существенно увеличивает вычислительную производительность. Разработанное программное обеспечение может быть расширено на заданное количество графических ускорителей, что отражено в диаграммах потоков, а увеличение видеокарт, в свою очередь, позволит моделировать большие расчетные области. Получены результаты моделирования, которые указывают на хорошее пространственно-временное согласие и качественное совпадение с выводами других исследований. Также проведен сравнительный анализ скорости выделения нефти в зависимости от диаметра отверстия: через классическую формулу утечки и путем моделирования.
1. Sokolovskiy E. V., Krivko V. V., Torbenko A. B. Vydelenie granic prirodnyh territoriy, podlezhaschih special'noy ohrane, sredstvami iskusstvennyh neyronnyh setey // Sovremennye tehnologii v deyatel'nosti osobo ohranyaemyh prirodnyh territoriy: geoinformacionnye sistemy, distancionnoe zondirovanie zemli: sb. tr. V Mezhdunar. nauch.-prakt. seminara (Naroch', 20-24 maya 2019 g.). Minsk: OOO «Binera», 2019. C. 127-129.
2. Fedotkin I. M. Matematicheskoe modelirovanie tehnologicheskih processov. M.: Lenand, 2015. 416 c.
3. Baskakov E. V., Savin E. S. Programmnyy kompleks dlya chislennogo modelirovaniya dinamiki perenosa primesey v atmosfere // XXVI Region. konf. molodyh uchenyh i issledovateley Volgograd. obl. (Volgograd, 17-24 noyabrya 2021 g.): tez. dokl. Volgograd: Izd-vo Volgograd. gos. un-ta, 2022. S. 351-358.
4. Li X., Chen G., Zhu H. Modelling and assessment of accidental oil release from damaged subsea pipelines // Marine Pollution Bulletin. 2007. V. 123. P. 133-141.
5. Patankar S. V. Chislennye metody resheniya zadach teploobmena i dinamiki zhidkosti. M.: Energoatomizdat, 1984. 152 s.
6. Suhinov A. I., Sidoryakina V. V., Procenko E. A., Procenko S. V. Chislennoe modelirovanie vozdeystviya vetrovyh techeniy na pribrezhnuyu zonu krupnyh vodohranilisch // Matematicheskaya fizika i komp'yuternoe modelirovanie. 2022. T. 25, № 3. S. 15-30.
7. Hrapov S. S., Agafonnikova E. O., Klikunova A. Yu., Radchenko V. P., Baskakov E. V., Savin E. S., Makoveev I. S., Hrapov N. S. Chislennoe modelirovanie samosoglasovannoy dinamiki poverhnostnyh vod, vlekomyh i vzveshennyh nanosov: I. Vliyanie promyshlennoy dobychi peska na bezopasnost' sudohodstva v rusle r. Volga // Matematicheskaya fizika i komp'yuternoe modelirovanie. 2022. T. 25, № 3. S. 31-57.
8. Hrapov S. S. Chislennoe modelirovanie samosoglasovannoy dinamiki poverhnostnyh i gruntovyh vod // Matematicheskaya fizika i komp'yuternoe modelirovanie. 2021. T. 24, № 3. S. 45-62.















