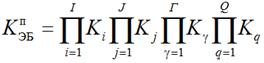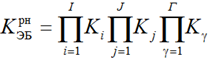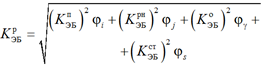Russian Federation
The article considers the urgent choice of a solution to the problem of reliable operation of power plants in the maneuvering modes. The performance reliability of power units is assessed. There are listed actual methods of studying the reliability of power plants, which are used in the practice of operation and design of power plants, in particular the electrical part in a statistical state. There is proposed a structural-functional method of studying the reliability of power plants, which allows to analyze the cause-and-effect relationships of the structural diagram elements in the stationary and transient modes of operation and obtain a synthesizing assessment of the final result of the power plant operation, taking into account the factors affecting the mode change. The scheme of directed graphs is illustrated: serial and parallel connection of elements, with direct and reverse stochastic connections. Formulas are given for calculating the availability factor (operability of an individual element or a functional circuit), as well as the inoperability factor due to the frequency of failures and remedial repairs. A case of practical application of the structural-functional method studying the reliability of power plants is considered. The elements of the block diagram of the power unit, turbine plant, electrical connections are listed. An algorithm for calculating the reliability of operation of a 250-300 MW power unit in the modes of start-up, shutdown, load control, stationary and emergency shutdown is considered. The logical sequence of operations of the technological process of the power unit is given. It is noted that the calculations were made on a personal computer in an interactive mode, labor costs amounted to about eight hours for an engineer of average qualification. According to the calculations performed, the conclusions were drawn for the power plant operating in the shunting mode as a whole: frequent starts/stops have a negative impact on the performance of power units, therefore, there is recommended a load mode within the allowable limits of power change.
structural-functional method, reliability, electric power system, graphs, power block
Введение
Проблема надежности функционирования энергоустановок в маневренных режимах электростанций сегодня не имеет законченного решения, поэтому остается актуальной. В настоящей статье предлагается решение отдельных задач этой проблемы, в частности оценка режимной надежности энергоблоков тепловой электростанции. Существующие методы исследования надежности энергоустановок (расчет групп или блоков структурно связанных элементов; топологические – с применением теории графов и определением минимальных путей и сечений; таблично-логические – при переборе событий отказов и ремонтов элементов; логико-вероятностные, основанные на представлении структурных схем логическими функциями или деревьями событий; графы состояний в форме однородных и неоднородных цепей Маркова и др.) применяются в практике проектирования и эксплуатации в основном электрической части энергоустановок, чаще всего в статическом состоянии. Оценка надежности энергоустановок в статическом состоянии – частное решение общей проблемы исследования надежности энергоустановок
в процессе функционирования, сочетающем стационарные и переходные режимы [1]. К последним относятся пуск, регулирование нагрузки, нормальный и аварийный остановы. Структурная схема, отражающая внутреннюю структуру и взаимосвязь элементов, является моделью исследования и анализа статической надежности энергоустановки. Она может изменяться под действием детерминированных или вероятностных (стохастических) факторов в переходных режимах. Совокупность отдельных режимов представляет собой процесс функционирования. Надежность функционирования энергоустановки – синтезирующая характеристика, отражающая внешнюю сторону процесса функционирования, оценивается вероятностью достижения конечного результата этого процесса [2].
Метод исследования надежности энергоустановок, учитывающий отмеченные особенности, получил название структурно-функционального метода (СФМ). Данный метод базируется на основных положениях теории направленных графов при анализе структурной надежности и на представлении процесса функционирования математической моделью логических операций при синтезе функциональной надежности. За основной параметр оценки надежности энергоустановок в СФМ принят коэффициент готовности.
Материалы и методы исследования
Структурные схемы строятся из технологически связанных между собой элементов, отдельные группы которых образуют функциональные цепи. Моделью функциональной цепи служит направленный граф, у которого узлы соответствуют коэффициентам готовности начального K0 и конечного Kn состояний цепи, а ветви – коэффициентам готовности элементов Ki, Kj [3].
В общем виде коэффициент готовности рассчитывается как
KГ = μ / (ω + μ).
В СФМ он получил название коэффициента работоспособности отдельного элемента или функциональной цепи. Противоположное состояние элемента характеризуется коэффициентом неработоспособности:
KН = 1 – KГ = ω / (ω + μ),
где ω, μ – частота отказов и восстановительных ремонтов соответственно, 1/год.
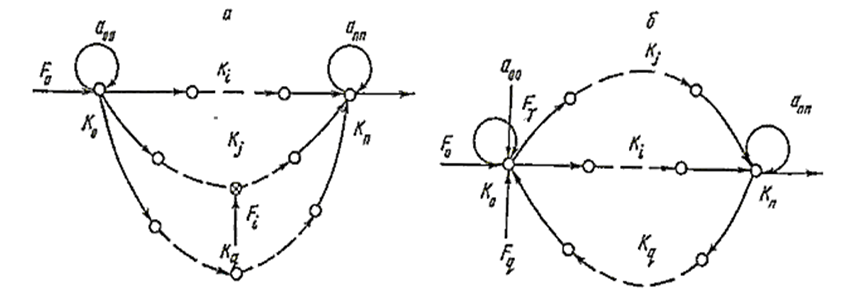
Узлы графа обладают собственными контурами a00, ann, к узлам отнесены действия факторов F, влияющих на изменение структурной схемы (рис. 1).
а б
Рис. 1. Виды направленных графов: а – последовательного и параллельного соединений элементов;
б – с прямыми и обратными стохастическими связями
Fig. 1. Types of directed graphs: a - serial and parallel connections of elements;
б - with direct and reverse stochastic connections
Собственные контуры в узлах графа a00; ann характеризуют результат диагностического контроля работоспособного состояния отдельных или группы связанных элементов.
Фактор F0 принимает дискретное значение 1 и 0 по результатам диагностического контроля.
Коэффициент работоспособности последовательно соединенных элементов получен путем решения уравнений, описывающих направленный граф (рис. 1, а), при начальных условиях: F0 = 1; a00 = ann = 1; Fi = 0,
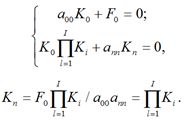(1)
Этот же граф представлен системой уравнений при начальных условиях: F0 = 1; a00 = ann = 1; Fi ≠ 0, т. е. при наличии фактора Fi, воздействующего на параллельную группу элементов и включающего ее в работу:
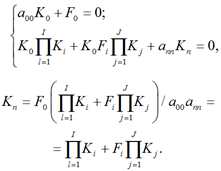(2)
При резервировании одной группы элементов другой:
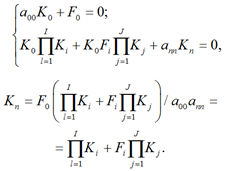(3)
В частном случае при Ki = Kj = K:
Kn = K + (1 – K)K = 2K – K2.
Если число параллельных ветвей больше двух (n > 2), то коэффициент работоспособности рассчитывается по известному выражению биноминального распределения:
(4)
где n – общее количество ветвей; m – количество рабочих ветвей; 
– число сочетаний.
Граф на рис. 1, б отражает структурную схему взаимосвязанных элементов, имеющих прямые и обратные связи, вступающие в работу под действием стохастических факторов Fγ или Fq.
При начальных условиях: F0 = 1; a00 = ann = 1;
Fγ ≠ 0; Fq = 0, т. е. при действии стохастического фактора Fγ, включающего в работу прямую связь коррекции, например при регулировании, граф представляется уравнениями относительно узлов начального K0 и конечного состояний Kn:
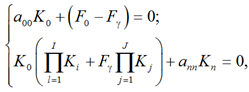
откуда
(5)
Обратная стохастическая связь, состоящая из
q-элементов, включается под действием фактора Fq. При начальных условиях: F0 = 1; a00 = ann = 1; Fγ = 0; Fq ≠ 0 – граф на рис. 1, б описывается уравнениями
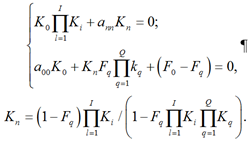(6)
Пример практического применения СФМ для оценки функциональной надежности энергоблока мощностью 250–300 МВт
Структурно-функциональный метод исследования надежности энергоблока (ЭБ) в стационарном и переходных режимах включает синтез показателей надежности отдельных функциональных элементов (эквивалентных элементов) на основе единого технологического цикла электрической и тепловой частей. В структурной схеме ЭБ мощностью 250–300 МВт выделены четыре расчетных элемента: парогенератор, турбинная установка, схема электрических соединений, система собственных нужд. В свою очередь, к парогенератору относятся элементы: собственно котла с поверхностями нагрева, газовоздушного тракта, трубопроводов питательной воды, паропроводов острого и перегретого пара, питательной установки, деаэратора, подогревателей, топливоподачи, растопочного устройства.
Структурные элементы турбинной установки: турбина, конденсаторная установка с циркуляционными и конденсатными насосами І подъема, эжекторами, обессоливающая установка с конденсатными насосами II подъема, валоповоротное устройство. К схеме электрических соединений отнесены элементы основного оборудования: турбогенератор, силовой трансформатор, коммутационные аппараты, отходящие линии, системы шин распределительного устройства. Собственные нужды включают основной блочный и резервный трансформаторы собственных нужд, системы шин и коммутационные аппараты. Электродвигатели и кабельные связи отнесены к соответствующему механизму собственных нужд электрической и тепловой частей ЭБ [4]. Каждый из перечисленных элементов структурной схемы представляется в виде направленного графа в соответствии с его внутренней структурной особенностью и рассматриваемым режимом. Согласно (1)–(6) производится математическое описание графов. Отдельные графы образуют функциональные цепи. Алгоритм расчета коэффициентов работоспособности ЭБ в режимах пуска, останова, регулирования нагрузки, стационарного и аварийного останова приведен в таблице, где φ – вероятность фактора режима F; 
– коэффициенты работоспособности ЭБ в соответствующих режимах: пуска, регулирования нагрузки, останова, стационарном, рабочего эквивалентного, аварийного останова; tr, tп, tо, tt, tрн – средняя продолжительность режимов: резерва, пуска, останова, ремонта, регулирования нагрузки, ч; ω, µр, λ – частоты отказов, плановых ремонтов и режимных отключений ЭБ, 1/год; Тв, Тр – продолжительность восстановительных и плановых ремонтов, ч;
N – количество рабочих суток ЭБ; М – количество ступеней в суточном графике нагрузки.
Алгоритм расчета надежности функционирования энергоблока 250–300 МВт
Algorithm for calculating the reliability of the operation of a 250-300 MW power unit
|
Режимы |
Вероятность |
Расчетные формулы |
Режимный коэффициент |
|||
|
Ki |
Kγ |
Kq |
Kj |
|||
|
Резерв |
|
– |
– |
– |
– |
– |
|
Ремонт |
|
– |
– |
– |
– |
– |
|
Пуск |
|
1 |
5 |
6 |
2; 3; 4 |
|
|
Регулирование |
|
1 |
5 |
– |
2; 3; 4 |
|
|
Останов |
|
1 |
5 |
6 |
2; 3; 4 |
|
Окончание таблицы
Ending of the Table
|
Режимы |
Вероятность |
Расчетные формулы |
Режимный коэффициент |
|||
|
Ki |
Kγ |
Kq |
Kj |
|||
|
Стационарный |
|
1 |
– |
– |
2; 3; 4 |
|
|
Рабочий |
– |
– |
– |
– |
– |
|
В связи с большим объемом вычислений разработана программа расчетов надежности функционирования ЭБ на ЭВМ в диалоговом режиме на основе логической последовательности операций (рис. 2). Программа может быть применена для ЭБ любой мощности, установленных на тепловой электростанции.
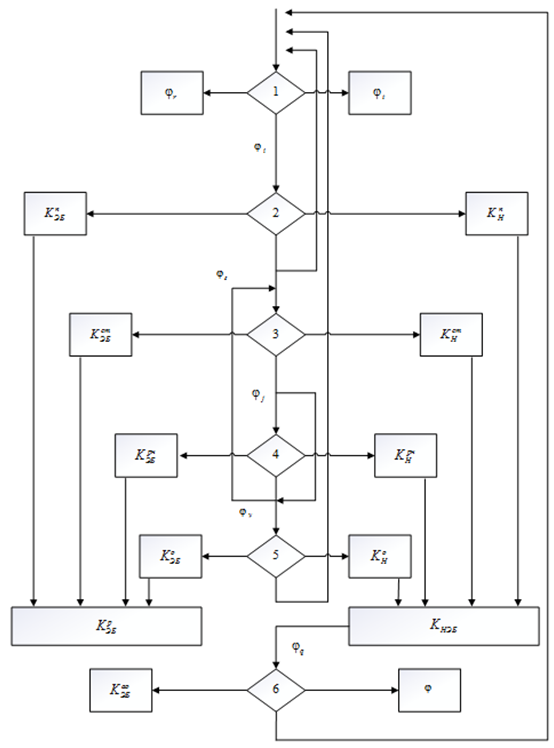
Рис. 2. Логическая последовательность операций технологического процесса энергоблока
Fig. 2. Logical sequence of operations of the technological process of the power unit
Результаты исследования
В результате исследования надежности ЭБ мощностью 250–300 МВт в стационарном и переходных режимах получены кривые зависимостей коэффициента работоспособности KЭБ от вероятностей возникновения режима φ. Расчетные функции приведены на рис. 3 со следующими обозначениями:
1 – стационарный режим;
2 – регулирование нагрузки;
3 – останов ЭБ;
4 – пуск ЭБ.
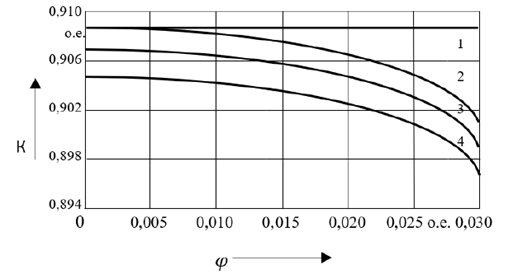
Рис. 3. Функции KЭБ = f(φ)
Fig. 3. Functions KЭБ = f(φ)
Для конкретного примера при заданных
φr = 0,126; φt = 0,229; φγ = 0,0035; φj = 0,0228; φi = 0,029; φs = 0,5897 коэффициенты работоспособности в соответствующих режимах:
Интегральный коэффициент работоспособности (см. табл.) будет равен 
вероятность режима аварийного останова φq = 0,371; коэффициент успешного аварийного останова 
, вероятность неуспешного аварийного останова с возможным развитием аварии φ = 0,0578.
Расчеты выполнялись на ПК в диалоговом режиме, трудозатраты составили порядка 8 ч для инженера средней квалификации. Определяющими факторами трудоемкости расчетов с помощью СФМ являются особенности технологических схем и состава оборудования тепловой и электрической частей ЭБ. Согласно результатам анализа надежности функционирования ЭБ в стационарном и переходных режимах может быть сделан вывод для электростанции в целом, работающей в маневренном режиме. Частые пуски и остановы снижают надежность энергоблоков, предпочтительнее использовать режим регулирования нагрузки в допустимых диапазонах изменения мощности.
Выводы
1. Предлагаемый СФМ исследования надежности энергоустановок позволяет анализировать причинно-следственные связи элементов структурных схем в стационарных и переходных режимах процесса функционирования и получить синтезирующую оценку конечного результата работы энергоустановки с учетом факторов, влияющих на изменение режима.
2. Данный метод расширяет возможности исследования надежности энергоустановок независимо от характера связей элементов структурных схем тепловой и электрической частей теплоэлектростанции.
1. Ancev I. B., Silenko V. N. Osnovy proektirovaniya vnutrennih elektricheskih setey. M.: Prospekt nauki, 2020. 272 c.
2. Baldin M. N. Osnovnoe oborudovanie elektricheskih setey: sprav. M.: NC ENAS, 2020. 671 c.
3. Bezopasnost' i nadezhnost' tehnicheskih sistem. M.: Universitet. kn.; Logos, 2021. 645 c.
4. Bulychev A. V., Navolochnyy A. A. Releynaya zaschita v raspredelitel'nyh elektricheskih setyah. M.: Enas, 2018. 208 c.
