Russian Federation
Russian Federation
Nizhny Novgorod, Russian Federation
Reducing the vessel hull vibration caused by the power equipment is usually obtained by the effective vibration-isolating fastening. Vibration impact on the mechanisms and automation tools greatly reduces their reliability, affects the health of passengers and crew members. Despite the modern vibration-insulating materials and compensators, the problems of eliminating the variable forces transmitted from the vibration source have not been fully solved. Increasing the operational requirements for the vibration safety of water transport requires the scientifically based and technical solutions, improving the designs of vibration isolation supports for mounting the marine power plants. Vibration reduction problems must be solved both at the design stage and at the stage of construction, repair and modernization. The conducted studies of vibrations under the influence of the harmonic force, step load and gradually increasing load have shown high efficiency of the support in all cases of load application under different simulation modes. At stabilization of the position the support was controlled by the integral of the displacement. The results of the studies conducted on the test model for the vibration protection of marine power equipment showed the effectiveness of the stabilizer. There is presented a theoretical study of a stabilizer with feedback on the displacement integral in the MathCAD software package. The numerical experiment is based on the Newton equation. The parameters of the stabilizer are determined, on the basis of which it is possible to design the actuator. It can be an electric motor, the direction of rotation of which depends on the direction of displacement of the protected object. The motor rotates a screw pair that compresses the spring. The spring acts on the clutch, the torque changes and maintains the vibration source. The simulation results helped to infer that it is necessary to stabilize the position of the unit for all load application modes.
power plant, vibration, vibration source, feedback, stabilizer, numerical experiment, displacement integral
Введение
Эффективность виброизоляции судового корпуса от вибрации механизмов и машин определяется возможностью снижения переменных сил, передаваемых от источника вибрации на судовой фундамент. Случай идеальной виброизоляции предполагает абсолютное постоянство силы, и этот метод получил название нулевая жесткость [1].
В течение последних семидесяти лет ученые, в частности И. И. Клюкин, П. М. Алабужев, А. К. Зуев, проводили исследования по снижению передаваемых сил, но полного успеха не удалось достигнуть по двум причинам. Во-первых, нулевая жесткость предполагает перестройку виброизолятора на иную нагрузку при смене режима работы источника вибрации, поскольку источник вибрации находится в неопределенном положении относительно основания. При этом эффективны только системы с подводом энергии, которые по ряду причин, например в связи с потерей устойчивости, не применяются в судостроении. Таким образом, возникает проблема перестройки виброизолятора. Во-вторых, упругий элемент в опоре передает вибрации, высокочастотный шум и создает резонансные режимы. Перечисленные проблемы в настоящее время не решены, поэтому задача снижения вибрации и создание судовой опоры с постоянным усилием является актуальной.
Материалы исследования
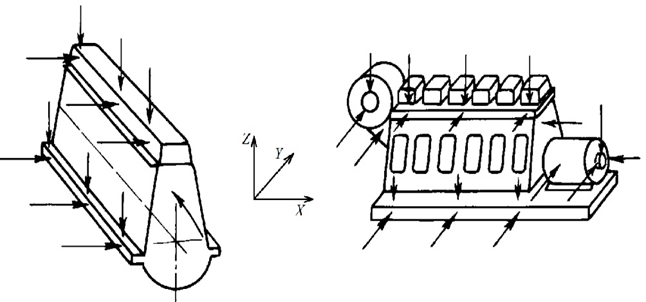
Для стабилизации положения энергетической установки используем силу, действующую против смещения и пропорциональную интегралу отклонения [1]. Для двигателей внутреннего сгорания и дизель-генераторов направление измерений вибрации обозначается по направлению осей: X – осевое (совпадающее с направлением коленчатого вала), Y – горизонтально-поперечное, Z – вертикальное. Точки измерения вибрации указаны на рис. 1 [2]. Сигнал по отклонению недопустим, поскольку равнозначен действию упругого элемента. Предварительными исследованиями установлено, что сигнал по интегралу отклонения не влияет на качество виброизоляции и его можно использовать для стабилизации [3–5]. Проинтегрируем уравнение динамики трижды, сменим знак и, помножив на выравнивающий коэффициент, получим сигнал для следящего привода. Ожидаемый результат – источник равномерно смещается в сторону полученного импульса, когда стабилизатор отключен, и останавливается, когда стабилизатор включен.
Источник вибрации управляется интегралом положения, из-за чего возникает статическая ошибка относительно нейтрального положения. Смещения в переходных процессах могут отрицательно сказываться на долговечности системы выпускного коллектора, труб охлаждающей воды и т. п. [6]. Одним из наиболее опасных из них является появление
и развитие в теле вала усталостных трещин, растущих с увеличением наработки гребного вала и приводящих к его окончательной поломке. Выход из строя водопровода приводит к финансовым потерям, во много раз превышающим стоимость разрушенного вала [7]. Судовые электростанции имеют неравномерную частоту вращения из-за скачков нагрузки, например при швартовке и погрузочных операциях.
а б
Рис. 1. Точки измерения вибрации и система координат главного двигателя (а) и дизель-генератора (б)
Fig. 1. Points of measuring vibrations and the coordinate systems of the main engine (a) and diesel generator (б)
В данной работе математическая модель не содержит упругих элементов, но в реальной опоре они есть, и это снижает качество виброизоляции. С другой стороны, неуказанная жесткость стабилизирует источник вибрации в реальной опоре [8–10]. Таким образом, возникает научно-методический вопрос об адекватности модели.
Поскольку расширение списка сил, действующих на источник, переводит задачу на другой уровень, было решено не учитывать жесткость связей и передачу вибрации через них на корпус. Положение источника вибрации относительно защищаемого основания является безразличным. Ранее было определено, что для стабилизации нельзя использовать упругие элементы. Рассмотрим действие стабилизатора источника вибрации. Уравнение динамики в этом случае содержит член, зависящий от интеграла смещения.
Анализ размерности коэффициентов, входящих в уравнение динамики, проведем для определения физических параметров исполнительного механизма. Основное уравнение записывается в нижнем ряду в размерности ускорения, первый интеграл над основным уравнением имеет размерность скорости, второй интеграл в третьем снизу ряду –
в размерности длины. Любое слагаемое уравнения динамики имеет размерность ускорения. Это же относится к управляющему действию R(q), пропорциональному интегралу смещения. По аналогии с пропорционально-интегральным регулятором коэффициент, выравнивающий размерность, будем называть коэффициентом передачи стабилизатора
R(q) = –kq1,
где k – коэффициент передачи стабилизатора; q1 – интеграл смещения с размерностью м·с.
Следовательно, коэффициент передачи стабилизатора [k] имеет размерность H/(м·с).
Физический смысл коэффициента: скорость изменения силы на один метр отклонения защищаемого объекта. Величина коэффициента выбирается достаточной для быстрой стабилизации, но меньше значения, приводящего к развитию автоколебаний.
![]()
где ![]() – ускорение массы, м/с2; m – масса, кг; f – амплитуда вынуждающей силы, Н; ω – угловая частота вынуждающей силы, рад/с; t – время, с; G – вес, Н; F(q) – сила компенсатора веса, Н; b – коэффициент вязкости демпфера, (Н·с)/м;
– ускорение массы, м/с2; m – масса, кг; f – амплитуда вынуждающей силы, Н; ω – угловая частота вынуждающей силы, рад/с; t – время, с; G – вес, Н; F(q) – сила компенсатора веса, Н; b – коэффициент вязкости демпфера, (Н·с)/м; ![]() – скорость массы, м/с.
– скорость массы, м/с.
В этом уравнении нет смещения, поскольку нет упругого элемента, как в традиционной опоре. Для численного решения запишем выражение в соответствии с процедурой rkfixed (рис. 2).
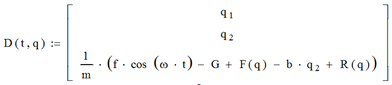
Рис. 2. Уравнение с интегрирующим элементом в программе Mathcad
Fig. 2. An equation with an integrating element in the Mathcad program
На этом основании можно проектировать исполнительный механизм. Это может быть электромотор, направление вращения которого зависит от направления смещения защищаемого объекта. Мотор вращает винтовую пару, которая сжимает пружину. Пружина действует на муфту, момент меняется и поддерживает источник вибрации.
Другой вариант исполнительного механизма содержит клапан, управляющий потоком жидкости, создающей давление на поршень, связанный с воздушной полостью управляющей силой прижатия дисков. При увеличении нагрузки клапан открывается, наполняет объем и увеличивает момент (поддерживающую силу) на муфте. Современный уровень таких устройств основан на микропроцессорной технике в сочетании с шаговым двигателем или с обычным двигателем и n-кодером. Составим численный эксперимент для определения параметров стабилизатора. Критерием действия стабилизатора является отклонение от среднего положения, а также статичность системы управления. На рис. 3 представлена модель ступенчатого воздействия на систему со стабилизатором, стабилизация положения (посередине) – на уровне 0,01 м. Воздействие узким импульсом можно задать двумя условными операторами (рис. 4). Установлено, что после воздействия импульса положение агрегата стабилизировалось на начальном уровне [11].
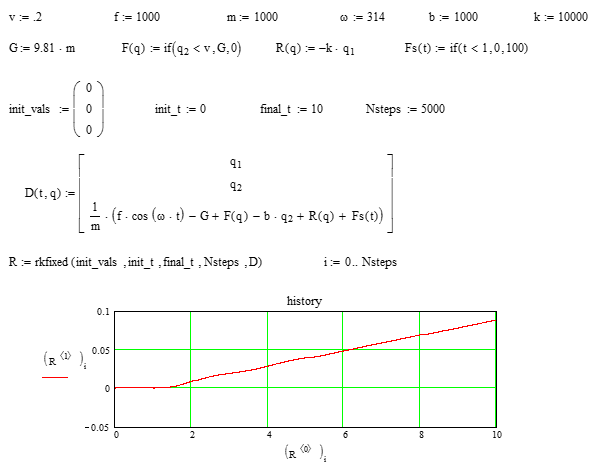
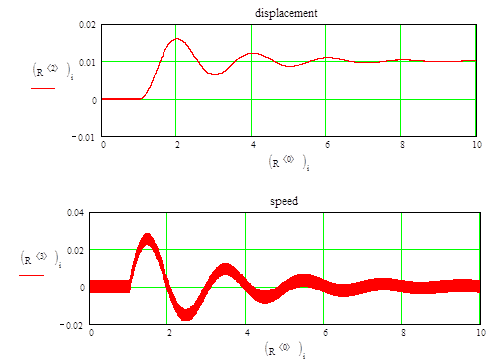
Рис. 3. Переходный процесс при ступенчатой нагрузке: а – исходные данные и математическое моделирование
процесса; б – зависимость интеграла перемещения массы от времени;
в – зависимость перемещения массы от времени; г – зависимость скорости колебаний массы от времени
Fig. 3. Transient process at stepped load: a - initial data and mathematical modeling of the process;
б - dependence of the mass displacement integral on time; в - dependence of mass displacement on time;
г - dependence of the mass oscillation rate on time
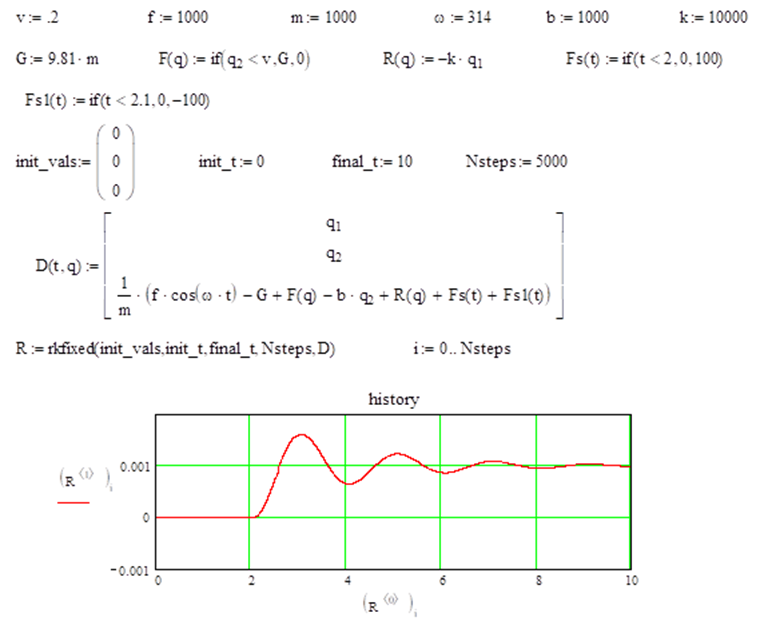
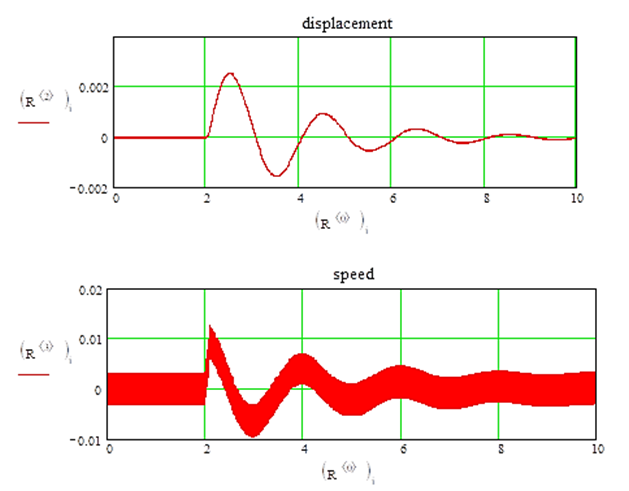
Рис. 4. Переходный процесс при узком импульсе: а–г (см. рис. 3)
Fig. 4. Transient process at a narrow pulse: а-г (Fig. 3)
Широкий импульс зададим теми же параметрами с большим промежутком по времени (рис. 5). Положение источника также установилось на среднем уровне.
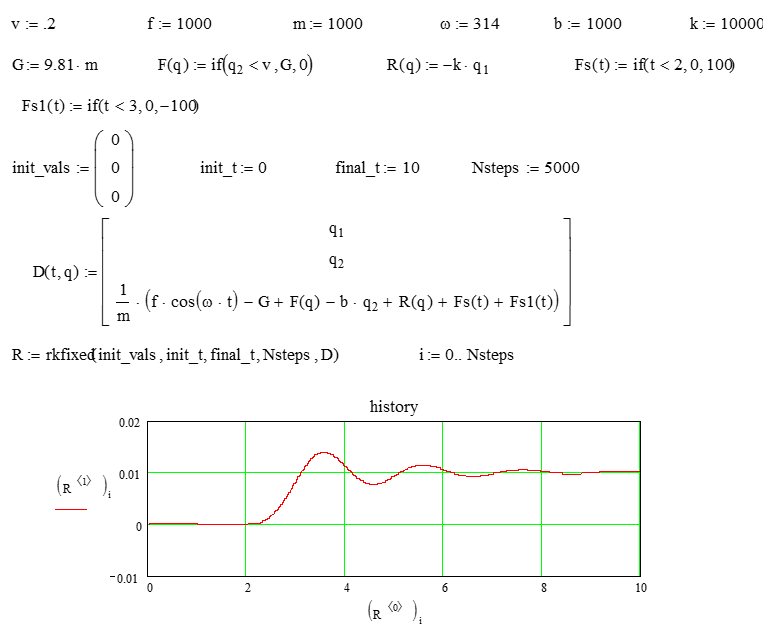
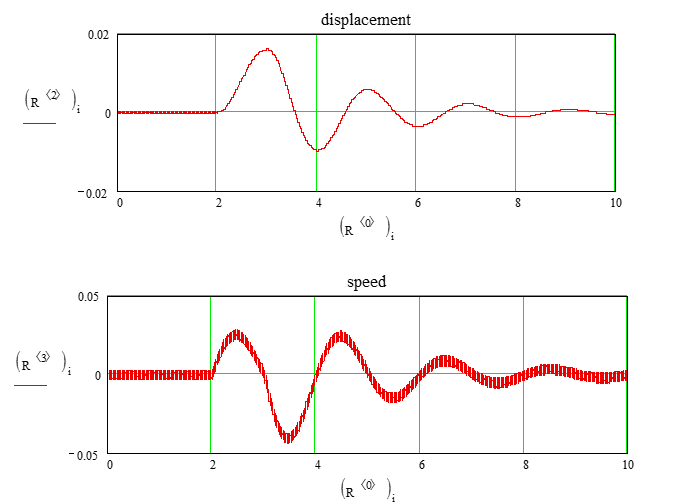
Рис. 5. Переходный процесс при широком импульсе: а–г (см. рис. 3)
Fig. 5. Transient process at a wide pulse: а-г (Fig. 3)
Таким образом, проведено исследование эффективности использовании стабилизатора на всех режимах работы энергетической установки.
Выводы
1. Математическое исследование реакции энергетического оборудования, проведенное для импульсов силы и ступенчатой нагрузки, выявило неограниченное смещение оборудования от действия любого, в том числе малого, импульса силы. Для судовых условий это недопустимо.
2. Математическое исследование реакции системы со стабилизатором при действии импульсов силы определило восстановление положения агрегата к первоначальному уровню.
3. Очевидна стабилизация положения агрегата во всех случаях приложения нагрузки, а значит, применение стабилизатора в системе обосновано.
1. Spiridonova A. N., Baranovskiy A. M. Metody stabilizacii v podveske nulevoy zhestkosti // Sibir. nauch. vestn. 2020. Vyp. XXIV. S. 19-23.
2. ND № 2-020101-124. Pravila klassifikacii i postroyki morskih sudov. Ch. VII. Mehanicheskie ustanovki. SPb.: Izd-vo RMRS, 2020. 107 s.
3. Baranovskiy A. M. Vibroizolyaciya dizeley rechnyh sudov. Novosibirsk: Izd-vo NGAVT, 2000. 176 s.
4. Babakov I. M. Teoriya kolebaniy. M.: Nauka, 1965. 560 s.
5. Baranovskiy A. M., Vikulov S. V., Spiridonova A. N. Metod snizheniya strukturnogo shuma sudovogo oborudovaniya // Rech. transp. (XXI v.). 2021. № 1 (97). S. 49-51.
6. Baranovskiy A. M. Vibracionnaya ocenka sudovyh mehanizmov // Sibir. nauch. vestn. 2012. Vyp. XVI. S. 107-111.
7. Matveev Yu. I., Orehvo V. A., Hramov M. Yu., Orehvo A. V. Osobennosti napressovki oblicovok grebnyh valov // Vestn. Volzh. gos. akad. vod. transp. 2019. № (60). S. 232-237.
8. Vibracii v tehnike: sprav. v 6-i t. / pod red. V. N. Chelomeya. M.: Mashinostroenie, 1984. T. 1. 352 s.
9. Baranovskiy A. M. Principy konstruirovaniya vibrozaschitnyh opor // Snizhenie strukturnogo shuma i vibracii na sudah: sb. nauch. tr. Novosibirsk: Izd-vo NGAVT, 2012. S. 4-6.
10. Baranovskiy A. M. Shumozaschitnaya opora sudovogo dvigatelya // Rech. transp. (XXI v.). 2010. № 3 (45). S. 72-73.
11. Spiridonova A. N. Vibrozaschita energetichesko-go oborudovaniya na osnove sistemy postoyannogo usiliya: dis. … kand. tehn. nauk. Novosibirsk, 2022. 153 s.

















