Russian Federation
Russian Federation
The article highlights the results of using a graph model of a continuous medium for solving elastic-plastic problems. The stress-strain state is determined by the method of variable parameters based on the deformation diagram of the medium material. The method is based on the representation of the defining elastic plasticity relations in the form of equations of linear elasticity theory, but with variable elasticity parameters. The computational process is an iterative procedure in which each successive approximation is reduced to solving a linear elastic problem. The problem is solved by the graph method. The stress-strain state is found by a non-standard numerical method in which a solid body is represented by a discrete model in the form of an oriented graph. Concrete examples show the high efficiency of the method in comparison with the traditional finite element method. The increased accuracy of calculations, even when using coarse grids, is ensured by the fact that: 1) the vertex and contour laws of graph theory implement the equations of equilibrium and compatibility of deformations for the element as a whole; 2) the equilibrium equations are performed locally by the volume of the element. The problems of the elastic-plastic bending of the console and the elastic-plastic state of a plate with a circular hole are solved as examples. Comparison of the obtained results with the solutions of these problems by other methods showed a good match. The high accuracy of calculations makes it possible to use the iterative procedure of the method of variable elasticity parameters as a subroutine in the application package created for the graph method.
theory of elasticity, theory of plasticity, graph model, graph method, calculation, elastic-plastic deformation
Введение
Проектирование современных конструкций с широким использованием в них структурно неоднородных материалов требует разработки эффективных методов расчета таких конструкций на прочность. Достижение этой цели невозможно без совершенствования известных и создания новых универсальных численных методов, моделирующих напряженно-деформированное состояние (НДС) структурно и механически неоднородных тел.
Среди различных численных методов, применяемых для расчета НДС, основными достаточно эффективными и широко распространенными являются метод конечных элементов и метод граничных элементов. Для этих методов характерно то, что дискретизации подвергается не сама среда на этапе ее моделирования, а уже созданная континуальная модель среды. В результате при численном моделировании процессов деформирования реальной среды могут быть допущены различные и трудно устанавливаемые погрешности, поэтому использование дискретных подходов на ранних этапах моделирования задач механики сплошной среды является оправданным и весьма перспективным.
В статье использован метод расчета полей деформаций и напряжений упругих тел, дискретной моделью которых служит ориентированный граф как идеализация гипотетических приборов, необходимых для измерения деформированного состояния тела. С помощью графового подхода дискретная модель среды может быть построена как первичная модель исследования, а не как некоторая аппроксимация исходной континуальной модели.
Процесс решения задач теории упругости с использованием графового метода состоит из следующих основных этапов:
1. Дискретизация, т. е. разбиение сплошной среды (конструкции) на некоторое количество подобластей – конечных элементов. При этом предполагается, что подобласти не пересекаются, т. е. не накладываются друг на друга и полностью заполняют исходную область.
2. Построение для каждого элемента зависимостей, связывающих усилия с деформациями (в рассматриваемом ниже случае – закон Гука), формирование матрицы жесткости элемента.
3. Сборка индивидуальных зависимостей в определяющую систему алгебраических уравнений, получение глобальной матрицы жесткости. На этом этапе существенную роль играет матричное представление структурных связей графа (для получения уравнений связной системы на основании уравнений ее частей используются матрицы контуров, путей, разрезов и хорд).
4. Решение полученной системы алгебраических уравнений.
5. Определение компонентов НДС.
Способ конструирования графовой модели, ее конфигурация, применение специальным образом сконструированных матриц для вывода определяющей системы уравнений применительно к плоской и осесимметричной задачам теории упругости предложены Е. Г. Кузовковым и подробно изложены
в [1–3]. В работе [4] на основе графовой модели построен двумерный сингулярный элемент для расчета напряженно-деформированного состояния в окрестности особых точек разреза. В статьях [5, 6] он был использован для моделирования НДС в окрестности центральной трещины в прямоугольной пластине. Графовая модель упругой среды в полярной системе координат рассматривалась в [7], а в работе [8] построена графовая модель трехмерного упругого тела в декартовой системе координат.
Метод упругих решений. Алгоритм итерационной вычислительной процедуры
По сравнению с задачами линейной теории упругости трудности в определении НДС пластических тел значительно возрастают. Однако при построении приближенных решений в ряде случаев их можно обойти. Существует класс задач, которые можно изучить методом упругих решений.
В его основе лежит метод линейных приближений. Итерационный процесс строится таким образом, что каждое следующее приближение сводится
к решению линейно-упругой задачи. Процесс последовательных приближений продолжается до тех пор, пока разница между двумя соседними приближениями не будет признана малой.
Метод переменных параметров [9] является одним из вариантов метода упругих решений. Он предложен И. А. Биргером и основан на представлении зависимостей упругопластического тела
в форме уравнений теории упругости, в которых параметры упругости зависят от напряженного состояния и потому их значения в различных точках отличаются друг от друга. Связь между компонентами тензора деформаций 
и компонентами тензора напряжений 
в теории малых упругопластических деформаций для двумерной задачи могут быть записаны в форме закона Гука [9]
(1)
где
(2)
– модуль Юнга и коэффициент Пуассона соответственно; 
– модуль упругости при сдвиге; σi – интенсивность нормальных напряжений; ɛi – интенсивность деформаций.
Так как значения в (2) неизвестны, то для расчета используется процесс последовательных приближений. В первом приближении полагают, что 
Тогда переменные параметры упругости равны упругим постоянным: 
. В результате решается обычная задача теории упругости и определяются напряжения 
, … и деформации 
, … в первом приближении. По этим величинам в каждой точке тела определяют интенсивности напряжений и деформаций .
При малых упругопластических деформациях для каждого материала между интенсивностью напряжений и интенсивностью деформаций существует определенная функциональная зависимость σi = Ф(ɛi), которая задается диаграммой деформирования аналитически или с помощью таблицы.
В случае сложного напряженного состояния зависимость σi – ɛi в каждой точке принимается такой же, как зависимость σ – ɛ при простом растяжении, т. е. 
[10].
На втором шаге для величины 
следует внести поправку и принять 
, где – интенсивность напряжений, которая соответствует интенсивности деформаций , взятой из диаграммы деформирования. По величинам по формулам (2) находят параметры , которые в разных точках тела различаются.
Зная эти параметры, вновь решают задачу упругости и определяют напряжения , деформации , …, а также интенсивность напряжений и интенсивность деформаций . Далее этот процесс повторяют, заканчивая расчет при достаточной близости двух соседних приближений.
Таким образом, решение задач теории пластичности сводится к решению последовательности задач линейной теории упругости. При этом метод расчета в упругой области предполагается известным. Таким методом обычно служит метод конечных элементов (МКЭ). Предлагаемый в статье метод является сочетанием метода последовательных упругих решений с последовательным изменением упругих характеристик материала и метода расчета НДС линейно-упругого тела с использованием графовой модели упругого тела.
Результаты численных расчетов
Результаты тестирования разработанного пакета прикладных программ, созданного на основе графового метода и предназначенного для решения упругих и упругопластических задач, представим на следующих примерах.
Пример 1. Решается задача об изгибе консольной балки, находящейся в плоском напряженном состоянии. Задача входит в узкий класс плоских задач теории упругости, которые тщательно изучались различными методами. Особенность этой конструкции в том, что при больших значениях отношения длины консоли L к высоте h элементы консоли совершают большие перемещения в качестве твердого тела при малых деформациях этих элементов. Ввиду плохой обусловленности с уменьшением шага сетки эта задача может оказаться труднореализуемой при ее решении численными методами. Известно, например, что многим конечным элементам свойственна неспособность передавать состояние чистого изгиба, а характер реагирования конечного элемента на этот вид нагрузки был назван «паразитическим сдвигом» [11].
Рассматривается консоль с упругими характеристиками: E =106 Н/м2 – модуль Юнга, v = 0,3 – коэффициент Пуассона, длина консоли L, высота h. Предполагается, что левый торец консоли закреплен, а к правому приложена равномерно распределенная нагрузка p = 10,0 Н/м2. Начало координат поместим в центре заделанного торца, ось OY направлена вдоль торца, ось OX – по длине.
Прежде чем решить упругопластическую задачу, представляется целесообразным проанализировать точность расчета на основе графовой модели для упругого тела. Сравним решения, полученные МКЭ и графовым методом. Определяется изгиб конца консоли в зависимости от отношения длины консоли L к высоте h (k = L / h), а также от числа степеней свободы; 16 степеней свободы соответствуют сетке 3 × 1; 42 – сетке 6 × 2; 130 – сетке 12 × 4 элементов.
В табл. 1 представлены результаты при k = 10 (L = 10 м, h = 1 м), полученные в работе [12] на трех типах конечных элементов, с расчетом на основе графовой модели.
Таблица 1
Table 1
Анализ точности расчетов вертикального смещения торца в зависимости
от числа степеней свободы
Analysis of accuracy of calculations of the vertical displacement of the end face depending
on the degrees of freedom
|
Тип элемента |
Число |
Число элементов |
Вертикальное смещение торца |
|
|
погрешность, % |
м |
|||
|
QUAD8s |
36 |
3 |
3,10 |
0,03876 |
|
QUAD91 |
42 |
3 |
1,58 |
0,03937 |
|
QUAD9t |
42 |
3 |
3,38 |
0,03865 |
|
Элемент графовой модели |
16 |
3 |
4,25 |
0,03832 |
|
42 |
12 |
0,72 |
0,03971 |
|
|
Теоретическое значение |
– |
– |
0 |
0,04000 |
В [12] использовались следующие конечные элементы: QUAD8s – 8-узловой серендипов, QUAD91 – 9-узловой лагранжев, QUAD9t – 9-зловой элемент, составленный из 2-х 6-узловых треугольных элементов.
В графовом методе используется 4-узловой прямоугольный элемент с 8 степенями свободы при аппроксимации поля деформаций линейными полиномами. Стандартный МКЭ для этого требует 16 степеней свободы (элементы с 8 узлами).
При равном числе степеней свободы графовая модель дает более точные результаты (см. табл. 1).
В последней строке табл. 1 в качестве теоретической величины прогиба на правом конце принято значение, получаемое в курсе сопротивления материалов (балочное приближение) по формуле
V = phL3 / (3EI); I = h3 / 12 – момент инерции прямоугольного сечения консоли, имеющей единичную ширину. Точное значение прогиба определяется формулой [1]
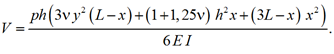(3)
В табл. 2 приведены полученные графовым методом отношения расчетных перемещений торца консоли в точке A(x =10, y = 0) к теоретическому значению (3) в зависимости от числа степеней
свободы.
Таблица 2
Table 2
Сравнение точности расчетов вертикального смещения торца
для конечно-элементного и графового методов
Comparison of accuracy of calculations of the vertical displacement
of the end face for the method of finite elements and graph method
|
L, м |
h, м |
k |
Vтeop, м |
V / Vтеор, % |
||
|
Число степеней свободы |
||||||
|
16 |
42 |
130 |
||||
|
10 |
2,00 |
5 |
0,01027 |
96,67 |
98,81 |
100,34 |
|
10 |
1,00 |
10 |
0,04028 |
95,09 |
98,59 |
99,61 |
|
10 |
0,5 |
20 |
0,16027 |
89,38 |
97,10 |
99,30 |
|
10 |
0,25 |
40 |
0,64027 |
72,05 |
91,26 |
97,69 |
При практическом применении численных методов важное значение имеет эффективность расчетной модели, под которой можно понимать достигаемую точность решения при фиксированном числе степеней свободы. Поэтому число степеней свободы можно считать некоторой обобщенной характеристикой возможностей метода, определяющей в конечном итоге вычислительные затраты. Как видно из табл. 2, с увеличением числа степеней свободы решение на графовой модели быстро приближается к точному решению.
Поскольку графовый метод позволяет найти численные решения линейных задач достаточно эффективно, можно ожидать, что эффективность сохранится и при решении последовательности упругих задач. В расчетах используем метод переменных параметров, основанный на формулах (1), (2). При решении упругопластической задачи используем диаграмму деформирования, представленную на рис. 1.
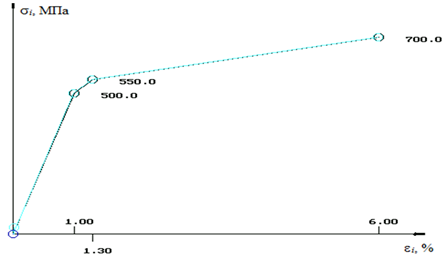
Рис. 1. Диаграмма деформирования упругопластического материала балки
Fig. 1. Diagram of deformation of elastic-plastic material of a beam
Диаграмма получена по вводимой таблично диаграмме растяжения и достаточно хорошо отражает зависимость из [12]. Процесс последовательных приближений, использующих диаграмму деформирования, описан выше. Итерации продолжаются до тех пор, пока во всех элементах
не станет 
.
При решении использовались прежние упругие параметры материала, а длина и высота приняты, как и в [13], L = 1 м, h = 0,4 м. На рис. 2 приведена деформированная сетка, иллюстрирующая известный факт о приближенно плоской форме деформируемых сечений, перпендикулярных оси балки.
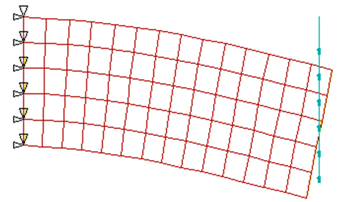
Рис. 2. Деформированная сетка при изгибе консольной балки
Fig. 2. Deformed mesh at a cantilever beam bending
Наконец, на рис. 3 сплошной и пунктирной линиями соответственно показаны эпюры напряжений , в сечении, равноудаленном от защемленного конца балки и конца, нагруженного равномерно распределенной нагрузкой.
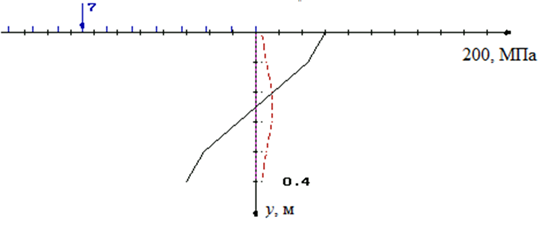
Рис. 3. Распределение нормальных и касательных напряжений в вертикальном серединном сечении
Fig. 3. Distribution of normal and shear stresses in the vertical middle section
Это упругопластическое решение хорошо согласуется с результатами из работы [13], полученными с помощью метода смягченных определяющих уравнений.
Пример 2. Рассмотрим теперь задачу о напряженном состоянии пластины с центральным круговым отверстием. Эта задача также входит в узкий класс плоских задач теории упругости, которые тщательно исследовались различными методами. Оценим напряженное состояние пластины размером 30 × 30 мм, которая ослаблена круговым отверстием радиусом 3 мм. Пластина в направлении оси х подвергается одноосно растягивающему напряжению интенсивности P = 300 МПа. Используются треугольные элементы графовой модели
с линейной аппроксимацией перемещений. В расчетах приняты следующие характеристики материала пластины: Е = 215 000 МПа – модуль Юнга;
ν = 0,3 – коэффициент Пуассона; σT = 650 МПа – предел текучести. Диаграмма деформирования материала представлена на рис. 4.
Диаграмма получена по вводимой таблично диаграмме растяжения. Процесс последовательных приближений, использующих диаграмму деформирования, описан выше. Итерации продолжаются до тех пор, пока во всех элементах не станет 
.
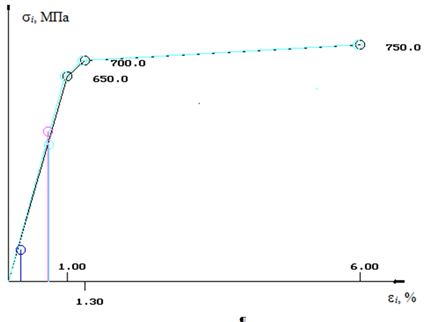
Рис. 4. Диаграмма деформирования материала пластины
Fig. 4. Diagram of the plate material deformation
Изучается плоское напряженное состояние пластины. Ввиду симметрии рассматривалась четверть всей области. Исследуемая область разбивалась на 720 треугольных элементов. В наиболее напряженных элементах, примыкающих к точке x = 0, y = 3,
отмечено появление зоны пластических деформаций.
На рис. 5 показано изменение напряжения σx вдоль оси пластины, перпендикулярной направлению растягивающей силы.
Рис. 5. Распределение напряжений в наиболее нагруженном сечении пластины
Fig. 5. Stress distribution in the most loaded section of the plate
Из рисунка видно, что при наличии упругопластических деформаций максимум напряжений
несколько сдвигается от контура отверстия вглубь пластины, в то время как в решении упругой задачи максимальная концентрация напряжений достигается на контуре отверстия.
Отметим, что с целью сравнения полученных результатов геометрические и физические параметры, принятые в расчетах, взяты такими, как при решении соответствующей задачи вариационно-разностным методом в [14]. Сопоставление эпюр напряжений, полученных на графовой модели и в [14], показало хорошее совпадение.
Численные расчеты графовым методом сравнивались также с результатами экспериментов по определению деформаций в пластине с отверстием
с весьма точным измерением упругопластических деформаций вблизи контура и на контуре [15].
В этой работе имеются данные экспериментальных замеров деформаций вдоль оси x = 0 пластины шириной 400 мм с отверстием диаметром 80 мм. Используя функциональную зависимость σi = Ф(ɛi) из работы [15] и определив деформации графовым методом, сопоставим результаты в табл. 3.
Таблица 3
Table 3
Сравнение экспериментальных замеров деформаций и деформаций,
определенных графовым методом
Comparison of experimental measurements of deformations and deformations
defined by the graph method
|
Показатель |
Значения |
|||||
|
Расстояние от центра отверстия, мм |
40 |
41 |
42 |
43 |
44,5 |
49 |
|
Экспериментальные данные, |
9,2 |
6,7 |
5,0 |
4,5 |
4,2 |
3,7 |
|
Расчет по графовой модели, |
9,8 |
6,9 |
5,3 |
4,7 |
4,4 |
4,0 |
Согласно данным, представленным в табл. 3, экспериментальные и расчетные значения с использованием предлагаемого численного метода хорошо согласуются.
Заключение
Показано, что графовый метод позволяет получать достаточно точные результаты на сетках с небольшим числом элементов и при фиксированном числе степеней свободы превосходит по своим возможностям стандартный МКЭ. Впервые графовая модель использована при расчете НДС в упругопластическом теле. Графовый метод можно применять не только в задачах линейной теории упругости, но и при решении упругопластических задач, нелинейных задач, в задачах теории трещин [5, 6] и других разделах механики твердого деформируемого тела.
1. Kuzovkov E. G. Grafovaya model' uprugoy sredy v dekartovoy sisteme koordinat // Problemy prochnosti. 1993. № 12. S. 60-70. DOI:https://doi.org/10.1007/BF00774638.
2. Kuzovkov E. G. Grafovaya model' uprugogo tela v smeshannyh peremennyh // Problemy prochnosti. 1986. № 6. S. 88-92. DOI:https://doi.org/10.1007/BF001523964.
3. Kuzovkov E.G. Axisymmetric Graph Model of an Elastic Solid // Problemy prochnosti. 1996. № 6. S. 83-103. DOI:https://doi.org/10.1007/BF02209319.
4. Tyrymov A. A. Singulyarnyy element grafovoy modeli uprugoy sredy v dekartovoy sisteme koordinat // Vychislitel'naya mehanika sploshnyh sred. 2011. T. 4, № 4. C. 125-136. DOI: org/10.7242/1999-6691/2011.4.4.47.
5. Tyrymov A. A. Chislennoe modelirovanie T-napryazheniy i koefficienta biaksial'nosti napryazhe-niy dlya obrazca s central'noy treschinoy pri smeshan-nyh granichnyh usloviyah // Vychislitel'naya mehanika sploshnyh sred. 2020. T. 13, № 4. S. 393-401. DOI:https://doi.org/10.7242/1999-6691/2020.13.4.30.
6. Tyrymov A. A. Chislennoe modelirovanie T-napryazheniy i koefficienta biaksial'nosti napryazheniy dlya obrazca s central'noy treschinoy na osnove grafovoy modeli uprugogo tela // Deformaciya i razrushenie materialov. 2021. № 6. S. 2-9. DOI:https://doi.org/10.31044/1814-4632-2021-6-2-9.
7. Tyrymov A. A. Grafovyy podhod pri postroenii konechno-elementnoy modeli uprugih tel v polyarnoy sisteme koordinat // Vestn. MGTU im. N. E. Baumana. Ser. Estestvennye nauki. 2017. № 3. S. 52-70. DOI:https://doi.org/10.18698/1812-3368-2017-3-52-70.
8. Tyrymov A. A. Uravneniya sostoyaniya grafovoy modeli trehmernyh uprugih tel v dekartovoy sisteme koordinat // Vestn. Perm. nac. issledovat. politehnich. un-ta. Mehanika. 2017. № 3. S. 188-202. DOI:https://doi.org/10.15593/perm.mech/2017.3.11.
9. Birger I. A. Nekotorye obschie metody resheniya zadach teorii plastichnosti // Prikladnaya matematika i mehanika. 1951. T. 15. Vyp. 6. S. 766-770.
10. Bezuhov N. I. Osnovy teorii uprugosti, prochnosti i polzuchesti. M.: Vyssh. shk., 1968. 512 s.
11. Cook R. Avoidance of parasitic shear in plane ele-ments // J. Struct. Div. Proc. Amer. Soc. Civil Engrs. 1975. V. 101, no. 6. P. 1239-1253. DOI:https://doi.org/10.1061/JSDEAG.0004075.
12. Cook W. A. The effect of geometric shape on two- dimensional finite elements // Nuclear Engineering and Desing. 1982. V. 70, iss. 1. R. 13-26. DOI: 1061/0029-5493(82)90263-1.
13. Kolarov D., Baltov A., Boncheva N. Mehanika plasticheskih sred. M.: Mir, 1979. 302 s.
14. Iosilevich G. B. Koncentraciya napryazheniy i defor-maciy v detalyah mashin. M.: Mashinostroenie, 1981. 224 s.
15. Panferov V. M. Koncentraciya napryazheniy pri uprugo-plastichnyh deformaciyah // Izv. AN SSSR. 1954. № 4. S. 47-65.
