Russian Federation
Russian Federation
Russian Federation
In modern conditions the food industry of the Russian Federation needs high quality natural emulsifiers, for example, lecithins. It should be noted that the carp caviar, in particular, the sazan caviar contains a large amount of lecithin. Analysis of the positive and negative aspects of different approaches to the freezing process and its structural design leads to the conclusion that it is reasonable to use (both from the point of view of technology, power consuming and economy) a conductive energy removal from the product that is in contact with the working surface of the cooling unit made in the form of a drum with a refrigerant supplied inside it. Given that it is difficult to empirically determine the temperature over the volume of the frozen object, it is advisable to simulate the processes of internal transfer of thermal energy and its exchange at the interfaces between the sample and the external environment, as well as the cooling surface of the drum. The aim of the study was a mathematical model solution about internal heat transfer during sazan caviar freezing under heterogeneous boundary conditions. The object of the study is a thin layer of the sazan caviar. Putting into practice the mathematical model of heat transfer, which describes freezing a 5 mm thick caviar product by the contact method by means of the finite difference method was realized by using the Mathcad Professional software product. In the process of solving the mathematical model of freezing, it was revealed that at the end of the freezing procedure, the average volumetric temperature of the caviar reaches its rational value of –7.5°C, after which the caviar product can be transported to the storage places. Rational operating parameters of the caviar product freezing process are: ambient air temperature up to 20°C; initial product temperature –10 ± 1°C; drum surface temperature up to –18°C; thickness of the frozen layer – 5 ± 0.5 mm; freezing time = 10 minutes.
lecithin, sazan caviar, heat transfer model, freezing, heat exchange, temperature, layer thickness
Введение
Повышение эффективности глубокой переработки сырья товарного рыбоводства, в том числе мало востребованной на российском рынке икры пресноводных рыб семейства карповых [1, 2], является важной и актуальной задачей. В современных условиях пищевая индустрия Российской Федерации нуждается в природных эмульгаторах высокого качества, к примеру, в лецитинах. Следует отметить, что карповая, в частности сазанья, икра содержит большое количество лецитина [3, 4] – около 10 000 мг в 100 г продукта [5]. Согласно данным Европейской ассоциации производителей лецитина, его мировое производство в настоящее время составляет более 250 тыс. т в год, а потребность – более 400 тыс. т в год [6, 7]. При повышающейся востребованности лецитина возникает вопрос выявления новой сырьевой базы для его получения. Известно, что на параметры лецитина преимущественно воздействует источник его выработки [3, 8], в котором необходимо максимально сохранить его целевые свойства при консервации до момента непосредственного использования в выбранной технологии. Самыми распространенными способами консервации являются сушка и замораживание исходного сырья. Замораживание является перспективным методом консервации, позволяющим максимально сохранить аромат, цветовую гамму, вкусовые ощущения и пищевую ценность материала.
Очевидно, что при выборе нового сырьевого источника для выработки лецитина резонно выявить определяющие ее научно-технические подходы к совершенствованию известных методов или найти оригинальные способы реализации ресурсо- и энергосберегающих технологий заморозки икры карповых рыб, а также их технического обеспечения.
Анализ позитивных и негативных сторон различных подходов к процессу замораживания [9–11] и его конструктивному оформлению приводит к выводу о резонности применения – как с технико-энергетической, так и с экономической точки зрения – кондуктивного энергоотвода от продукта контактирующей с ним рабочей поверхностью охлаждающей установки, выполненной в виде барабанного узла с подведенным внутрь него холодильным агентом. Учитывая, что среднеобъемную температуру объекта замораживания эмпирически определить сложно, целесообразно провести моделирование процессов внутреннего переноса тепловой энергии и обмена ею на границах раздела между образцом и внешней средой, а также охлаждающей поверхностью барабана.
Цель исследования – построить, адаптировать к икре сазана и решить математическую модель внутреннего теплопереноса в процессе замораживания при разнородных граничных условиях.
Объекты и методы исследования
Объектом исследования является тонкий слой икры сазана. Процесс переноса тепловой энергии внутри твердого тела с учетом ее обмена на его границах с внешней средой, описывается известным дифференциальным уравнением теплопроводности [12–14], в котором искомая функция T = T(r, τ) задает температуру в точке тела с координатами r в момент времени τ:
![]() ,
,
где ![]() – интенсивность варьирования Т в течение процедуры заморозки во времени τ, град/с; а – показатель температуропроводности, м2/с;
– интенсивность варьирования Т в течение процедуры заморозки во времени τ, град/с; а – показатель температуропроводности, м2/с; ![]() – дифференциальный оператор Лапласа; r – принятая координатная система,
– дифференциальный оператор Лапласа; r – принятая координатная система, ![]() – функция тепловых источников.
– функция тепловых источников.
Исследуемые процессы переноса тепловой энергии в объекте холодильной обработки и обмена ею на границах раздела между ним и внешней средой, а также охлаждающей поверхностью барабана происходят при отсутствии внутреннего источника теплоотвода, т. е. ![]() , в этом случае имеем
, в этом случае имеем
![]() . (1)
. (1)
Уравнение (1) в частных производных подходит для описания основной массы процедур теплопроводности, и с целью выявления из них наиболее подходящего резонно сформулировать особенности данной операции, для чего схематично представим физическую интерпретацию предлагаемого способа замораживания икры сазана, консервируемой холодом (рис. 1).
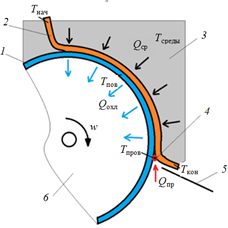
Рис. 1. Схема контактного замораживания сазаньей икры:
1 – замораживающая поверхность барабана; 2 – замораживаемый продукт;
3 – воздушная среда; 4 – горячая струна для съема продукта с барабана;
5 – наклонная полка для удаления замороженного продукта в камеру хранения; 6 – вращающийся барабан;
Тнач – начальная температура объекта заморозки; Тсреды – температура окружающей среды; Тпов – температура
поверхности барабана; Тпров – температура натянутой струны; Ткон – конечная температура объекта заморозки;
Qср – тепловая энергия среды, подводимая к объекту заморозки; Qохл – отводимая тепловая энергия
от объекта заморозки; Qпр – тепловая энергия струны, подводимая к объекту заморозки;
w – скорость вращения барабана
Fig. 1. Graph of contact freezing of sazan caviar:
1 – freezing surface of the drum; 2 – frozen product; 3 – air environment; 4 – hot string for removing the product
from the drum; 5 – inclined shelf for transferring the frozen product to the storage room;
6 – rotating drum; Тнач – initial temperature of a freezing object; Тсреды – environmental temperature;
Тпов – drum surface temperature; Тпров – tensioned string temperature; Ткон – final temperature of the freezing object;
Qср – thermal energy of environment supplied to the freezing object; Qохл – thermal energy diverted from a freezing object; Qпр – string thermal energy supplied to a freezing object; w – drum rotation
Ввиду малой толщины слоя замораживаемого продукта (5 мм) при большой ширине и протяженности рабочей поверхности барабанного полотна слой объекта исследования можно уподобить бесконечной пластине, т. е. не учитывать его торцевые поверхности и за координату в сетчатом векторе принять глубину слоя по толщине, а за вторую координату, которая и принята в уравнении теплопереноса (1), целесообразно взять время проводимой процедуры.
В итоге уравнение (1) примет следующий вид:
![]() , (2)
, (2)
где х – глубина по слою образца, м; τ – длительность замораживания, с.
Как видно, соотношение (2) является уравнением 1-го порядка по длительности операции τ и 3-го порядка по пространственной координате х.
Итак:
– исходная величина х на поверхности слоя у поверхности барабанного узла: xn = 0;
– итоговая величина х у противоположной открытой поверхности слоя: xk = 0,005;
– фиксация времени в начале процедуры: τ = 0;
– фиксация времени в конце процедуры: τ = xk.
В теоретических положениях обычных дифференциальных соотношений для частного их решения определяют граничные условия по пространственной координате. Также для решения соотношения в частных производных определяются краевые, в частности граничные, условия, которые ранжируются на несколько типов, в частности на условия 1-го и 2-го родов. Условия 1-го рода характеризуются, когда на границе задается значение искомой функции, в нашем случае это температура, а граничные условия 2-го рода характеризуются, когда на границе в исследуемом ареале задается не определяемый функционал, т. е. варьирование непосредственно Т, а тепловой поток [15–17].
Таким образом, в месте соприкосновения замораживаемого продукта с поверхностью барабана зададимся граничными условиями первого рода, т. е. примем, что температура на поверхности барабана постоянна на протяжении всего процесса теплообмена и равна Тпов, и только при достижении у образца заданной конечной температуры Tкон заменим Тпов на Тпров, которая соответствует температуре нагретой струны. В месте соприкосновения замораживаемого продукта с воздушной средой зададимся условиями 2-го рода:
![]() ,
,
где α – коэффициент теплоотдачи, Вт/(м2 ∙ К); Тсреды – температура для воздушной среды при взаимодействии с охлаждаемым образцом, °С; Тнач – температура для граничного слоя материала при взаимодействии с воздухом, °С.
Реализация математической модели теплопереноса (2), описывающей замораживание икорного продукта толщиной в 5 мм контактным способом, посредством способа конечных разностей, решена с помощью программного продукта Mathcad Professional.
Результаты и их обсуждение
Согласно представленной схеме икорный продукт толщиной 5 мм, имеющий начальную температуру Тнач = 10 °С, при контакте с поверхностью вращающегося барабана, имеющей температуру Тпов = –18 °С, начинает замораживаться. Отметим, что объект консервирования с другой стороны контактирует с воздушной средой, имеющей температуру Тсреды = 20 °С, которая выше Тнач, что оказывает негативное влияние на скорость замораживания икры. Заметное преобладание отводимой тепловой энергии Qохл от продукта заморозки над подводимой к продукту теплотой от внешней воздушной среды Qср в итоге приводит к желаемому результату, и по прошествии некоторого времени в икре достигается заданная среднеобъемная отрицательная температура Tкон.
Скорость вращения барабана w регулируется таким образом, чтобы путь, проделанный продуктом при непосредственном контакте с поверхностью барабана, не превышал половину длины его окружности. Очевидно, что при контакте икорного продукта с поверхностью барабана, имеющей отрицательное значение температуры Тпов, между ними произойдет прочное сцепление, которое затруднит удаление замороженной икры из морозильной установки. Для решения этой проблемы в морозильном устройстве барабанного типа предусмотрен узел отделения замороженной икры от холодной поверхности, который представляет собой нагретую до температуры Тпров натянутую струну, расположенную прямо на поверхности вращающего барабана перпендикулярно движению икорного продукта. Подводимая от струны теплота Qпр прямо по линии контакта продукта с поверхностью барабана моментально ликвидирует прочное сцепление между ними, практически не влияя на среднеобъемную температуру замороженной икры, что позволяет под действием силы тяжести удалить ее из секции заморозки и направить на дальнейшее хранение посредством любого транспортирующего устройства.
На рис. 2 графически представлено решение адаптированной к объекту исследования математической модели теплопереноса, а именно скорость продвижения фронта Т по слою замороженного икорного продукта, меняющая свою величину в зависимости от продолжительности процесса, реализуемого в рабочей камере барабанного морозильного аппарата.
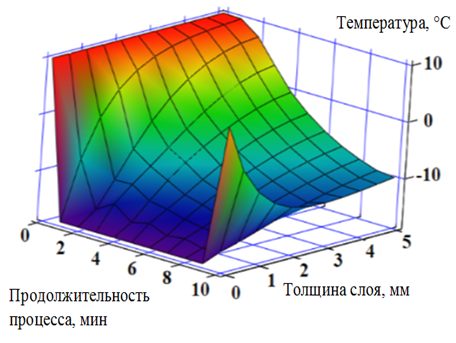
Рис. 2. Скорость продвижения фронта Т по толщине слоя продукта во времени при замораживании сазаньей икры
Fig. 2. Rate of moving the front T along the thickness of the product layer in time during the sazan caviar freezing
Из графика видно, что температура поверхностного слоя продукта, контактирующей с охлаждающей рабочей поверхностью барабанного узла, изначально резко снижается до температуры данной поверхности и впоследствии становится равной ей. При этом на последней стадии обозначенной операции температура поверхности продукта начинает повышаться вследствие взаимодействия с нагретой (с целью минимизации адгезии между материалом и рабочей поверхностью установки) струной, предназначенной для съема замороженной продукции. С противоположной открытой поверхности слоя продукта, контактирующей с окружающей средой, при теплообмене путем ее естественной конвекции температура плавно уменьшается, но с меньшей интенсивностью по сравнению с обратным вариантом, описанным выше. Сделанные выводы с точки зрения теплообмена очевидны и не требуют детального физического пояснения.
Для более наглядного понимания полученных результатов решения математической модели процесса замораживания икры из сазана на рис. 3 показан график варьирования ее среднеобъемной температуры и температур на границах объекта холодильной обработки в зависимости от продолжительности замораживания.
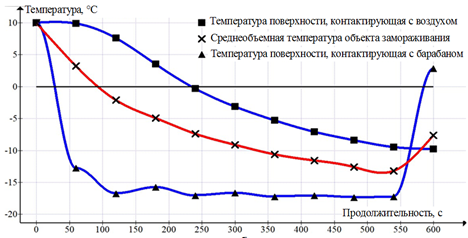
Рис. 3. График изменения среднеобъемной температуры объекта холодильной обработки
и температур на его границах в зависимости от времени замораживания
Fig. 3. Graph of changing the average volumetric temperature of the refrigeration object
and temperatures at its boundaries depending on the freezing time
В таблице представлены значения температур по толщине объекта заморозки, изменяющихся в зависимости от продолжительности этого процесса, на основании которых построены графики на рис. 2 и 3.
Значения температур по толщине объекта при его замораживании, °С
Temperature values for the thickness of the object when it is frozen, °С
|
Толщина слоя, мм |
Продолжительность замораживания, с |
||||||||||
|
0 |
60 |
120 |
180 |
240 |
300 |
360 |
420 |
480 |
540 |
600 |
|
|
0 |
10 |
9,906 |
7,646 |
3,574 |
–0,271 |
–3,089 |
–5,315 |
–7,059 |
–8,395 |
–9,454 |
–9,765 |
|
0,5 |
10 |
9,674 |
7,295 |
3,037 |
–0,78 |
–3,586 |
–5,816 |
–7,555 |
–8,888 |
–9,948 |
–10,20 |
|
1,0 |
10 |
9,372 |
6,501 |
2,023 |
–,638 |
–4,341 |
–6,542 |
–8,203 |
–9,517 |
–10,54 |
–10,59 |
|
1,5 |
10 |
8,934 |
5,221 |
0,527 |
–2,804 |
–5,371 |
–7,467 |
–9,01 |
–10,27 |
–11,22 |
–10,92 |
|
2,0 |
10 |
8,266 |
3,37 |
–1,413 |
–4,248 |
–6,68 |
–8,567 |
–9,975 |
–11,14 |
–11,99 |
–11,08 |
|
2,5 |
10 |
7,223 |
0,835 |
–3,702 |
–5,953 |
–8,251 |
–9,813 |
–11,1 |
–12,10 |
–12,85 |
–10,95 |
|
3,0 |
10 |
5,579 |
–2,481 |
–6,192 |
–7,946 |
–10,03 |
–11,18 |
–12,38 |
–13,13 |
–13,81 |
–10,32 |
|
3,5 |
10 |
2,98 |
–6,582 |
–8,697 |
–10,30 |
–11,90 |
–12,72 |
–13,75 |
–14,22 |
–14,85 |
–8,854 |
|
4,0 |
10 |
–1,136 |
–11,23 |
–11,11 |
–13,09 |
–13,68 |
–14,52 |
–15,07 |
–15,46 |
–15,87 |
–6,106 |
|
4,5 |
10 |
–7,66 |
–15,66 |
–13,72 |
–16,12 |
–15,35 |
–16,62 |
–16,22 |
–16,96 |
–16,73 |
–1,414 |
|
5,0 |
10 |
–18 |
–18 |
–18 |
–18 |
–18 |
–18 |
–18 |
–18 |
–18 |
7 |
Следует отметить, что в конце процедуры замораживания среднеобъемная температура икры, судя по рис. 3 и данным таблицы, достигла своего рационального значения в –7,5 °С, при котором икорный продукт может транспортироваться в места хранения. Ниже представлены разработанные рациональные режимные параметры процесса замораживания икорного продукта:
– температура окружающего воздуха – не выше 20 °С;
– начальная температура продукта – 10 ± 1 °С;
– температура поверхности барабана – не выше –18 °С;
– толщина замораживаемого слоя – 5 ± 0,5 мм;
– продолжительность замораживания – 10 мин.
Заключение
Построена, адаптирована к икре сазана и решена методом конечных разностей математическая модель внутреннего теплопереноса в процессе замораживания при разнородных граничных условиях. Научная новизна приведенных в статье результатов решения математической модели (как в графической, так и в табулированной интерпретации (см. рис. 2, 3, табл.)), заключается в том, что аналитическая и численная реализация адаптированной к объекту исследования математической модели позволила оценить температурные поля по толщине слоя икры в зависимости от режимных факторов, вида теплоносителя и способа энергоподвода. Отметим, что приведенные результаты не входят в конфликт с известными данными других исследователей, подтверждены экспериментально и, следственно, могут быть использованы в инженерной практике.
Разработанные режимные параметры замораживания икорного продукта в морозильниках барабанного типа могут успешно использоваться при реализации технологии лецитина из сазаньей икры, т. к. позволяют сохранить в объекте обработки необходимый целевой компонент.
1. Dobreckaya E. I. Rynok rybnoy produkcii v Rossiyskoy Federacii // Molodoy uchenyy. 2022. № 13. S. 44-47.
2. Kolonchin K. V., Betin O. I., Voloshin G. A., Gorbunova M. A. Analiz cen rybnoy produkcii na vnutrirossiyskom rynke // Tr. VNIRO. 2021. T. 185. S. 113-119. DOI:https://doi.org/10.36038/2307-3497-2021-185-113-119.
3. Vol'nova E. R., Kozyreva A. S., Lyashenko A. E. Razlichnye sposoby polucheniya lecitina iz produktov rastitel'nogo i zhivotnogo syr'ya // Molodoy uchenyy. 2021. № 17. S. 28-32.
4. Butina E. A., Gerasimenko E. O., Bugaets I. A., Du-brovskaya I. A. Comparative analysis of the physiological value of lecithins obtained from different types of raw materials // Journal of Pharmaceutical Sciences and Research. 2017. V. 9. N. 12. P. 2493-2497.
5. Popov V. G., Belina S. A., Fedorova O. S. Razvitie tehnologii proizvodstva specializirovannyh produktov pitaniya dlya naseleniya Arktiki // Polzun. vestn. 2017. № 3. S. 14-18.
6. Lisovaya E. V., Viktorova E. P., Lisovoy V. V. Analiz assortimenta lecitinov, predstavlennyh na rossiyskom rynke // Tehnologii pischevoy i pererabatyvayuschey promyshlennosti APK - produkty zdorovogo pitaniya. 2019. № 2. S. 51-55.
7. Mortensen A., Aguilar F., Crebelli R., Di Domenico A., Jose M. et al. Re-evaluation of lecithins (E 322) as a food additive // EFSA Journal. 2017. V. 15. N. 4. Article e04742. DOI: https://doi.org/10.2903/j.efsa.2017.4742.
8. Zharkova I. M., Rudakov O. B., Polyanskiy K. K., Roslyakov Yu. F. Lecitiny v tehnologiyah produktov pitaniya. Voronezh: Izd-vo VGUIT, 2015. 256 s.
9. Soroko O., Usenya Yu. Analiz sposobov zamorazhivaniya pischevyh produktov // Nauka i innovacii. 2011. T. 5. № 99. S. 63-67.
10. Eremenko V. T., Oreshina M. N. Metodologicheskie aspekty matematicheskogo modelirovaniya teplo-massoobmennyh processov na primere zamorazhivaniya termolabil'nyh materialov // Informacionnye sistemy i tehnologii. 2020. T. 119. № 3. S. 47-55.
11. Ishevskiy A. L., Davydov I. A. Zamorazhivanie kak metod konservirovaniya pischevyh produktov // Teoriya i praktika pererabotki myasa. 2017. T. 2. № 2. S. 43-59.
12. Aktershev S. P., Alekseenko S. V., Cvelodub O. Yu. Teoreticheskoe modelirovanie gidrodinamiki i teploperenosa v volnovyh plenkah zhidkosti pri slozhnyh usloviyah techeniya (obzor) // Teplofizika i aeromehanika. 2022. T. 29. № 1. S. 1-36.
13. Nugmanov A. H. H., Maksimenko Yu. A., Aleksanyan A. I., Aleksanyan O. A. Issledovanie fiziko-himicheskih svoystv rybnyh farshey, suhih rastitel'nyh premiksov i ih smesey // Vestn. Astrahan. gos. tehn. un-ta. Ser.: Rybnoe hozyaystvo. 2018. № 2. S. 135-148. DOI:https://doi.org/10.24143/2073-5529-2018-2-135-148.
14. Cirlin A. M. Matematicheskie modeli i optimal'nye processy v makrosistemah. M.-Berlin: Direkt-Media, 2015. 500 s.
15. Eremenko V. T., Oreshina M. N. Metodologicheskie aspekty matematicheskogo modelirovaniya teplo-massoobmennyh processov na primere zamorazhivaniya termolabil'nyh materialov // Informacionnye sistemy i tehnologii. 2020. № 3. S. 47-55.
16. Aleksanyan I. Yu., Nugmanov A. H. H., Yarceva N. V., Hudaliev Yu. M., Aysungurov N. D. Modelirovanie kinetiki teplomassoperenosa v processe vakuumnogo zamorazhivaniya rybnogo farshevogo syr'ya // Nauch. zhurn. NIU ITMO. Ser.: Processy i apparaty pischevyh proizvodstv. 2020. № 2. S. 11-21. DOI:https://doi.org/10.17586/2310-1164-2020-10-2-11-21.
17. Popov N. M. Issledovanie algoritma resheniya differencial'nogo uravneniya teploprovodnosti metodom konechnyh raznostey // Avtomatizaciya i energosberezhenie v mashinostroenii, energetike i na transporte: sb. tr. Vologda: Izd-vo Volog. gos. un-ta, 2022. S. 236-241
















