Russian Federation
Russian Federation
Syktyvkar, Russian Federation
In solving the problems of assessing the reliable hydrocarbon deposits the initial data are considered in the form of fuzzy relationships, which is possible by constructing a stray field that is a fuzzy modeling method based on the data compression algorithm. This algorithm allows reducing the quantity dimension and taking away the random information from the initial data, which is a possible cause of an erroneous estimate. The data compression algorithm has two stages. The first stage is based on a clustering algorithm that helps locate the data sources. The second stage is based on the Hooke-Jeeves method of calculating the source weight. Experiments were carried out to study the influence of the number of sources on the result of building the stray field. A set of petrophysical parameters (porosity by GWL, pore sizes in cores) measured at one time was used as initial data, which characterized the capacitive properties of the rock. Each experiment is supplied with the maps of sources, stray fields and relative errors. It has been inferred that with a decreasing the source number the stray fields saved their structure, though there increased the relative error of a stray field and of the map of initial data density.
fuzzy relations, reliability assessment, hydrocarbon reserves, number of data sources, stray field, density map
Введение
Оценка достоверности измеренных параметров играет важную роль при подсчете запасов углеводородов, т. к. данный подсчет выполняется в условиях неопределенности. Достоверность в дальнейшем позволяет рассчитывать экономические риски разработки месторождений [1, 2].
В процессе подсчета запасов выполняется одновременное измерение на одном образце породы значений петрофизических параметров, которое содержит случайную («ошибочную») информацию и ошибки при измерении. При проведении экспериментов часто появляется «ошибочная» информация. Данные ошибки могут искажать результаты интерпретации геофизических данных и служить основой неверных заключений. Чтобы избавиться от случайной информации, исходные данные необходимо рассматривать как нечеткие отношения. Основанием для представления данных в форме нечетких отношений служит понятие поля рассеяния, которое предлагается строить на основе алгоритма сжатия информации. Алгоритм сжатия информации позволяет снизить размерность величин и избавиться от случайной информации, присутствующей в наборе исходных данных, подразумевается, что исходные данные получены от источников информации (физический смысл источников основан на представлении о том, что рассчитанное значение поля рассеяния, следующее из экспериментальных данных, – это результат диффузии от источников информации) и являются откликом от данных источников, который фиксируется при проведении экспериментов.
Целью применения алгоритма является поиск наименьшего количества источников, при которых невязка между картой плотности исходных данных и рассчитанным полем рассеяния удовлетворяет заданному условию.
Цель исследования заключается в повышении качества оценки достоверности петрофизических моделей, используемых при подсчете запасов углеводородов.
Постановка задачи
Пусть 𝔄 – исходные данные, представляющие собой матрицу размерностью M × L, где M – количество измерений, а L – количество параметров. Строка матрицы есть вектор одновременно измеренных параметров. Матрица исходных данных имеет следующий вид:
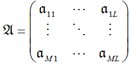 .
.
Исходные данные покрываются сеткой S размерностью Nl, l = 1 ÷ L, где N – количество ячеек в измерении [3], и рассчитывается карта плотности данных 𝔄(s), где s – набор ячеек сетки.
Размер ячейки r = r1 × r2 × … × rL вычисляется по формуле
![]()
где m – порядковый номер измерения; l – порядковый номер параметра; N – количество ячеек в измерении. Карта плотности 𝔄(s) характеризует относительную частоту данных в каждой ячейке сетки (количество одновременно измеренных значений параметров в ячейке сетки относительно общего числа измерений внутри эксперимента).
Поле рассеяния представляет собой линейную комбинацию функций экспоненциальной модели [4]:
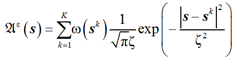
где ε – погрешность, с которой выполняется расчет поля рассеяния; s – набор ячеек сетки, для которой выполняется расчет; K – количество источников информации; sk – ячейка, в которой расположен k-й источник; ω(sk) – вес k-го источника; ζ – эффективный параметр, влияющий на рассеяние данных.
Предложенная модель имеет принцип максимальной энтропии, т. е. информация, полученная от источников – это итог диффузии, которая длилась определенное время.
Решение задачи заключается в распределении источников sk и нахождении их веса ω(sk). Решение задачи основано на представлении о том, что рассчитанное значение поля рассеяния, следующее из экспериментальных данных, – это результат диффузии, который привел к сглаживанию более точной зависимости ω(sk):
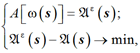 (1)
(1)
где A – оператор для расчета поля рассеяния.
Алгоритм решения задачи состоит из двух этапов: на первом этапе решается задача расположения источников, на втором – подбор веса источников.
Решение задачи
Первый этап. Для определения местоположения источников на сетке воспользуемся алгоритмом кластеризации. Кластеризация – разбиение исходных данных на кластеры. Кластеры представляют собой группы со схожими характеристиками, которыми, в нашем случае, являются значения одновременно измеренных параметров.
В основе алгоритмов кластеризации лежит критерий сравнения объектов, которым, как правило, является расстояние. Для расчета расстояния была выбрана метрика квадрата евклидова расстояния
ρ между объектами x и x':
![]()
где n – количество характеристик объекта; i – порядковый номер характеристики объекта.
В качестве алгоритма кластеризации для решения поставленной задачи был выбран метод
k-средних, позволяющий построить оптимальное решение (выбор координат источников) на основе минимизации суммарного квадратичного отклонения объектов кластера от центров данных кластеров:
![]()
где ![]() – набор кластеров.
– набор кластеров.
Входными данными для решения задачи кластеризации являются вектор значений параметров и количество источников. Выбранный метод удобен тем, что рассчитанные центры кластеров будут использованы в качестве координат источников данных.
Второй этап. Для решения задачи (1) в рамках второго этапа с целью расчета весов источников в точках (центров кластеров), полученных на первом этапе, можно воспользоваться алгоритмом Хука – Дживса. Данный метод относится к методам прямого поиска экстремума функции и состоит из исследующего поиска и поиска по образцу. Исследующий поиск предназначен для определения направления минимизации. Поиск по образцу заключается в изменении параметров функции вдоль выбранного направления. Метод Хука – Дживса широко применяется при решении инженерных задач [5].
Эксперименты
В качестве исходных данных для расчетов использовался набор одновременно измеренных значений между параметрами карбонатных пород Салюкинского месторождения Тимано-Печорской нефтегазовой провинции (рис. 1, а).
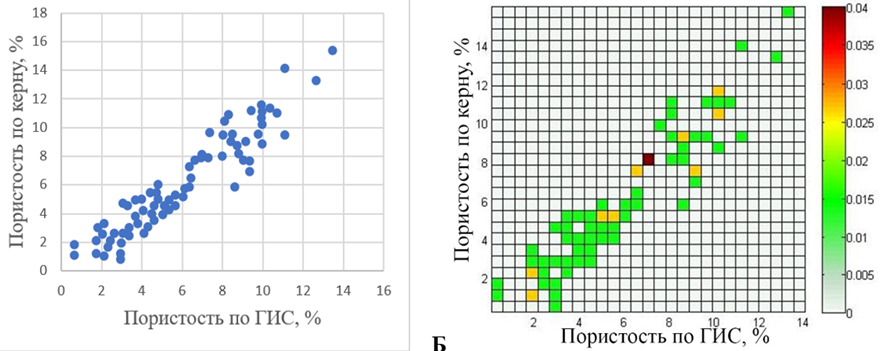
Рис. 1. Исходные данные: набор одновременно измеренных значений между параметрами «Пористость по ГИС»
и «Пористость по керну» (а); карта плотности исходных данных (б)
Fig. 1. Initial data: a set of simultaneously measured values between the parameters “Porosity by logging”
and “Core porosity” (а); a map of source data density (б)
Характеристики исходных данных:
1) параметры:
– пористость по ГИС (объем пор относительно общего объема горной породы, рассчитанный на основе интерпретации результатов геофизических исследований скважин);
– пористость по керну (рассчитывается на основе анализа кернового материала);
2) количество измеренных значений – 75.
Для вычислений частоты данных, карты источников и поля рассеяния была выбрана расчетная сетка S размером 25 × 25. Полученная карта плотности данных 𝔄(s) представлена на рис. 1, б. Большинство ячеек с данными принимают значение 0,1, а максимум составляет 0,04.
Было проведено 3 эксперимента. По каждому эксперименту были построены карты источников данных и поля рассеяния:
1) для первого эксперимента при решении задачи кластеризации было выбрано 52 источника (рис. 2);
2) для второго – 37 источников (рис. 3);
3) для третьего – 22 источника (рис. 4).
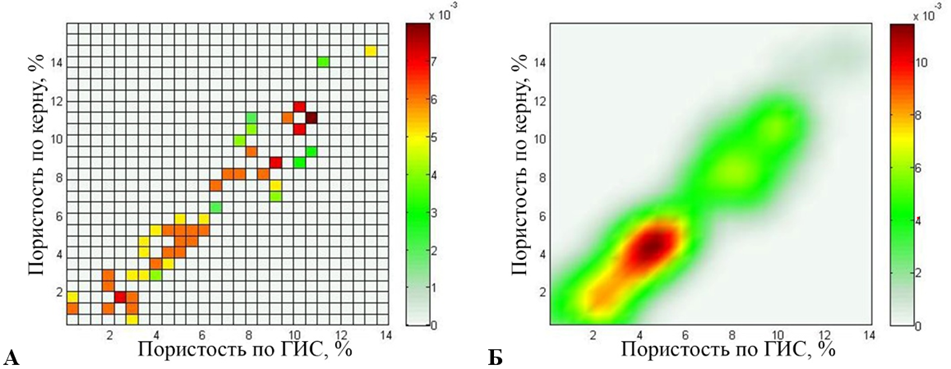
Рис. 2. Первый эксперимент (52 источника): карта источников (а) и поле рассеяния (б)
Fig. 2. First experiment (52 sources): a source map (a) and a stray field (б)
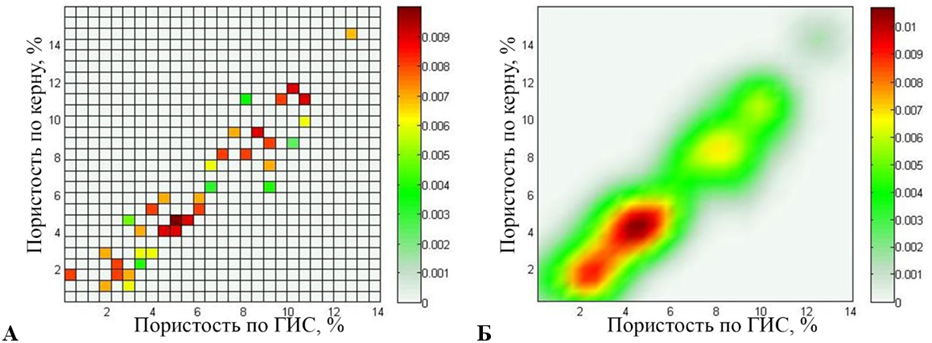
Рис. 3. Второй эксперимент (37 источников): карта источников (а) и поле рассеяния (б)
Fig. 3. Second experiment (37 sources): a source map (a) and a stray field (б)
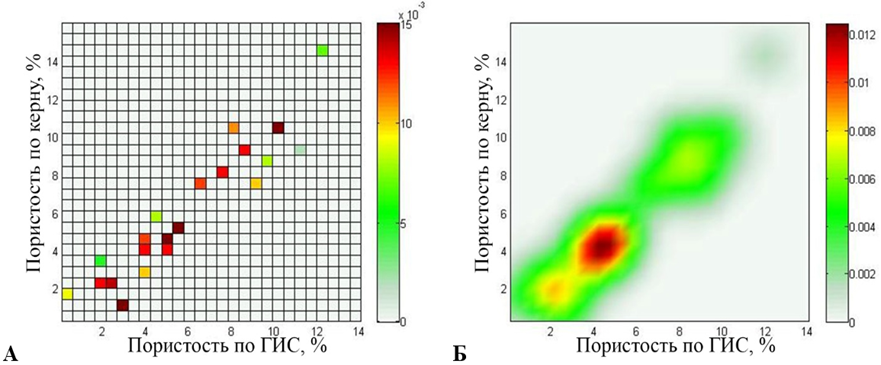
Рис. 4. Третий эксперимент (22 источника): карта источников (а) и поле рассеяния (б)
Fig. 4. Third experiment (22 sources): a source map (a) and a stray field (б)
Карта источников отображает местоположение источников, полученное на первом этапе, и веса источников, полученные на втором этапе. Поле рассеяния является основой для представления данных в форме нечетких отношений и используется для оценки алгоритма сжатия информации путем сравнения данного поля с картой плотности. Вертикальная цветовая шкала справа на рис. 2–4 отображает числовые значения источников и поля рассеяния в палитру.
Измеренные значения данных параметров имеют высокую степень локализации, но наблюдается различная плотность данных на разных участках. Поле рассеяния сохраняет структуру данных, позволяя использовать все исходные данные, не искажая их, но при этом ранжируя данные по достоверности. В дальнейшем подобные нечеткие петрофизические модели используются совместно с геологическими 3D-моделями, отображая достоверность подсчетов запасов углеводородов.
Карта источников, полученная в результате проведения первого эксперимента, принимает значения в диапазоне от 0 до 0,008. Поле рассеяния принимает значения в диапазоне от 0 до 0,0114. Относительная погрешность поля рассеяния и карты плотности исходных данных составляет 4,7 %:
![]()
Карта источников, полученная в результате проведения второго эксперимента, принимает значения в диапазоне от 0 до 0,01. Поле рассеяния принимает значения в диапазоне от 0 до 0,0106 с относительной погрешностью 4,73 %.
Максимальное значение на карте источников, полученной в результате проведения третьего эксперимента, составляет 0,015. В свою очередь, максимальное значение поля рассеяния составляет 0,0124 с относительной погрешностью 4,76 %.
В рамках экспериментов были рассчитаны поля рассеяния, где количество источников постепенно уменьшалось от 67 до 2. В качестве демонстрации выше были представлены результаты трех экспериментов для 52, 37 и 22 источников соответственно, а на рис. 5 представлена динамика изменения погрешности вычислений относительно всего возможного набора количества источников данных.
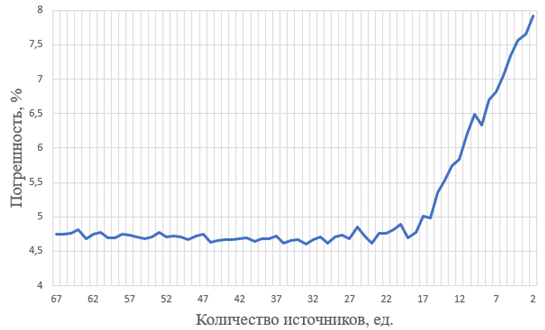
Рис. 5. Динамика изменения погрешности вычислений относительно количества источников данных
Fig. 5. Dynamics of changes in calculation errors relative to the number of data sources
Проведенные эксперименты демонстрируют, что поле рассеяния, вне зависимости от количества источников, сохраняет свою структуру, однако относительные погрешности поля рассеяния и карты плотности при выборе количества источников из диапазона от 67 (90 % от исходных данных) до 17 изменяются незначительно, а с 17 значение погрешности начинает увеличиваться.
Выводы
1. Для распределения источников информации при представлении набора одновременно измеренных значений параметров можно использовать алгоритм кластеризации, в частности, основанный на метрике квадрата евклидова расстояния.
2. Для расчета весов источников допустимо использовать метод Хука – Дживса.
3. Уменьшение количества источников с определенного момента приводит к увеличению погрешности между полем рассеяния и картой плотности данных. Рост погрешности указывает на то, что поле рассеяния начинает существенно отличаться от исходных данных, теряя тем самым неоднородную структуру данных, учет которой важен при подсчете запасов углеводородов.
4. Следующим этапом является определение критерия уменьшения количества источников. Цель данного критерия заключается в определении минимально допустимого количества источников, которое позволит избавиться от случайной информации, присутствующей в наборе исходных данных.
1. Altunin A. E., Semuhin M. V. Sravnitel'nyy analiz ispol'zovaniya veroyatnostnyh i nechetkih metodov ocenki neopredelennosti i riskov pri podschete zapasov i resursov uglevodorodov // Neftyanoe hozyaystvo. 2011. № 9. S. 44-49.
2. Altunin A. E., Semuhin M. V., Yadryshnikova O. A. Metody analiza neopredelennostey geologo-promyslovyh sistem i nechetkie imitacionnye modeli // Avtomatizaciya, telemehanizaciya i svyaz' v neftyanoy promyshlennosti. 2015. № 5. S. 33-43.
3. Kozhevnikova P. V., Kuncev V. E., Chuvashov A. A. Vliyanie shaga raschetnoy setki pri postroenii funkciy prinadlezhnosti otnosheniy mezhdu petrofizicheskimi parametrami // Sovremennaya nauka: aktual'nye problemy teorii i praktiki. Ser.: Estestvennye i tehnicheskie nauki. 2021. № 7. S. 65-70.
4. Kobrunov A. I., Dorogobed A. N., Kozhevnikova P. V. Matematicheskoe modelirovanie nechetkih petrofizicheskih zavisimostey // Sovremennye naukoemkie tehnologii. 2018. № 10. S. 50-55.
5. Huk R., Dzhivs T. A. Pryamoy poisk resheniya dlya chislovyh i staticheskih problem. M.: Mir, 1961. S. 212-219.















