Russian Federation
Russian Federation
Russian Federation
Performance of external longitudinal and transverse forces developed in the course of towing the trawl systems, namely, the tension and compression forces of cables, ropes and yarns of the rope-net gears in commercial fishing of the longitudinal modulus of elasticity and the transverse modulus of elasticity in the cordage products. Physical and mechanical properties of the synthetic nylon threads, ropes and nylon cords, from which most trawl systems are made, are considered. Analysis of the physical and mechanical properties of synthetic rope products and cords based on the specified parameters for possible static and dynamic loads is proposed. Algorithms for calculating the physical and mechanical properties of threads, ropes and nylon cords are proposed under the condition of constant volume and mass. Method of calculating physical and mechanical properties of the nylon threads and ropes under the condition of uncertainty gives an error not exceeding 0.4% in calculating the relative elongation δε, but the maximum error δμ in calculating Poisson's ratio μ reaches 7.12%. This proves that the formula for calculating the Poisson's ratio μ for anisotropic bodies does not allow estimating this ratio at low loads and constant volume.
trawl system, force performance, cordage article, sennit cord, calculation, load, longitudinal and transverse forces, module of elasticity
Введение
Расчет физико-механических свойств синтетических крученых канатно-веревочных изделий (КВИ), а также плетеных шнуров (ПШ) является неотъемлемой частью проектирования траловых комплексов. Обоснование диаметра и разрывной нагрузки КВИ и ПШ необходимо выполнить при создании технико-рабочего проекта трала. Это обусловлено прочностью канатов канатных связей, веревок и ниток делей, из которых создана траловая конструкция.
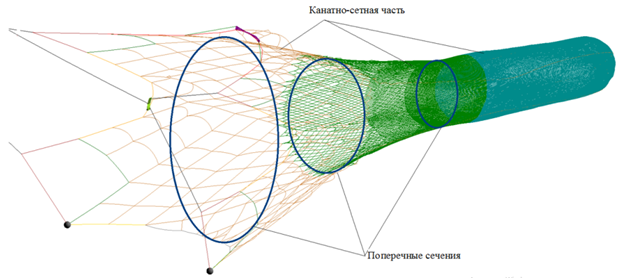
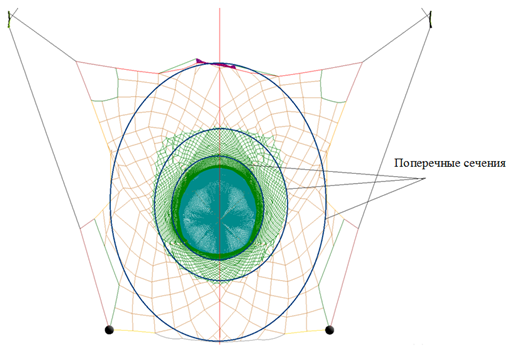
В существующих методиках обоснования диаметра и разрывной нагрузки КВИ и ПШ траловых конструкций принимается во внимание гидродинамическое сопротивление, распределенное по поясам канатно-сетной части трала, при этом не учитывается ни шворка, ни съячейка, а также форма траловой оболочки в поперечном сечении [1], что сказывается при обосновании прочностных характеристика канатов и дели. Задают повышенный коэффициент прочности n КВИ и ПШ, а это отражается на стоимости траловой конструкции. На рис. 1 изображена канатно-сетная часть разноглубинного трала и поперечные сечения вдоль его оболочки.
а
б
Рис. 1. Канатно-сетная часть разноглубинного трала: а – вид в аксонометрии; б – вид поперечной плоскости
Fig. 1. Rope-net part of a mid-water trawl: a – axonometric view; б – transverse view
Поперечные сечения, как правило, делают в местах соединения канатных связей и съячеивания сетных пластин. Гидродинамическое сопротивление рассчитывается по поясам с помощью алгоритма [2]. При этом расчет ведется в статике с учетом постоянства среднего взвешенного угла атаки траловой оболочки, что является ошибочным, т. к. алгоритм расчета гидродинамического сопротивления канатно-сетной оболочки получен для целого трала, а не его участков, и в этом случае неизвестны длины образующих поясов и их форма. Неточное определение углов ориентации КВИ и ПШ, а также неучет съячейки и шворки и влияния динамических нагрузок приводят к ошибочным расчетам сил натяжения в КВИ и ПШ, таким образом, коэффициент запаса прочности n снова повышают.
На рис. 2 изображены соединения сетных пластин (отрезков делей) и канатных связей съячейкой и шворкой (шворочный шов).
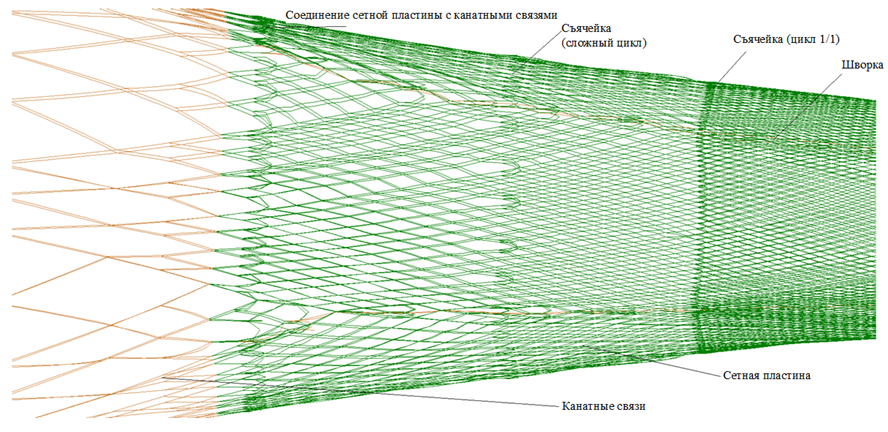
Рис. 2. Соединения канатно-сетной части разноглубинного трала
Fig. 2. Connections of the rope-net part of the mid-water trawl
Как видно, трал (при соответствующих оснастке, длине ваеров, параметрах траловых досок и скорости траления) может менять свою форму от устья до тралового мешка [1], причем нагрузки в КВИ и ПШ напрямую зависят от формы поперечного сечения, соединения сетных пластин, канатных связей, а также углов ориентации КВИ и ПШ в пространстве. Данными углами также пренебрегают в расчетах и обоснованиях прочностных характеристик траловой конструкции, и осреднение угла атаки меридиана траловой оболочки приводит к большим погрешностям в расчетах.
Таким образом, неправомерно распределять на канатные связи, веревки и шнуры равномерно по поясам гидродинамическое сопротивление канатно-сетной части трала. Это может привести к аварийным ситуациям, таким как порывы сетных пластин, обрыв подборы, канатной связи и т. д.
Обратим внимание на производительность сил траловой системы (далее ТС) [3]. Производительность внешних продольных и поперечных сил, создаваемых при буксировке траловых систем, а именно сил натяжения и сжатия канатов, веревок и ниток канатно-сетного орудия промышленного рыболовства, связана с продольным модулем упругости и поперечным модулем упругости КВИ [4].
Введем допущения:
– КВИ и ПШ рассматриваются как идеально гибкие цилиндрические изделия, которые подвержены продольному растяжению и сжатию и поперечному сжатию;
– при исследовании КВИ и ПШ не учитывались такие конструктивные параметры, как свивка, количество прядей, толщина проволоки и волокна, тип плетения;
– при исследовании КВИ и ПШ не учитываются внутренние силы трения между волокнами и прядями КВИ;
– объем КВИ и ПШ при нагрузке не изменяется
(V = const).
Постановка задачи
Рассмотрим задачу расчета физико-механических свойств капронового изделия (каната, веревки или нитки) физико-механических свойств ПШ дели тралового мешка на основании заданных параметров при возможной статической и динамической нагрузке. Так как КВИ и ПШ имеют в сечении условную окружность, то примем, что ось OZ совпадает с осью OY и OX при вращении КВИ и ПШ [2]. Запишем уравнения, характеризующие физико-механические свойства для идеально гибких КВИ и ПШ, связывающие конструктивные, геометрические и силовые их характеристики при условии постоянства их объема V = const:
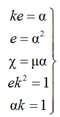, (1)
где k – коэффициент пропорциональности, k = f(ε, λ), ε – относительная продольная деформация, λ – конструктивное удлинение (конструктивный параметр); e – отношение модулей упругости; α – безразмерное сужение, α = f(ε, λ), т. е. α = 1/k; χ – безразмерная компенсационная сила; μ – коэффициент Пуассона.
Запишем основные выражения для КВИ и ПШ, входящие в (1):
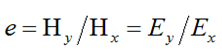, (2)
где Hy – производительность условных поперечных сил; Hx – производительность условных продольных сил; Ey – поперечный модуль упругости; Ex – продольный модуль упругости:
, (3)
где L – длина КВИ и ПШ; d – диаметр КВИ и ПШ;
, (4)
где Tdy – компенсационная сила (противодействия Ty) в поперечном направлении (вдоль оси OY); Tlx – компенсационная сила (противодействия Tx) в продольном направлении (вдоль оси OX);
; (5)
, (6)
где Tx – приложенная сила растяжения (вдоль оси OX); Ty – сила сжатия (вдоль оси OY); εd – относительная поперечная деформация;
(7)
Рассмотрим систему (1), добавив выражение, связывающее конструктивное удлинение, коэффициент Пуассона и α КВИ и ПШ. Таким образом, систему (1) можно переписать в виде
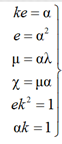, (8)
при условии коэффициент Пуассона μ
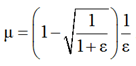. (9)
Отметим, что коэффициент Пуассона μ для анизотропных тел зависит от изменения объема КВИ и ПШ, в таком случае примем, что коэффициент Пуассона μ зависит от параметров
, (10)
где ν – безразмерный объем; θ – безразмерная плотность; ξ – композитность (неоднородность); ζ – крутка (плетение).
Безразмерный объем ν и безразмерная плотность θ связаны выражением (масса КВИ и ПШ m = const)
. (11)
Пренебрегая композитностью (неоднородный или смешанный) ξ и круткой (плетением) ζ, получим
,
или через относительное сужение КВИ и ПШ
, (12)
где Δd – изменение диаметра (уменьшение).
Для анизотропного материала (КВИ и ПШ) коэффициент Пуассона
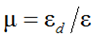(13)
это доказывает проведенные экспериментальные исследования [5].
Параметр χ
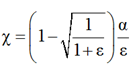. (14)
На основании вышеприведенных формул
(1)–(9) и (14) приведем два алгоритма (условие определенности и условие неопределенности) расчета зависимости физико-механических свойств КВИ и ПШ от действующей нагрузки в продольном сечении, связывающие конструктивные, геометрические и силовые их характеристики при условии V = const и m = const (рис. 3 и 4). В алгоритме на рис. 3 приводится приложенная гипотетическая сила растяжения Fxp.
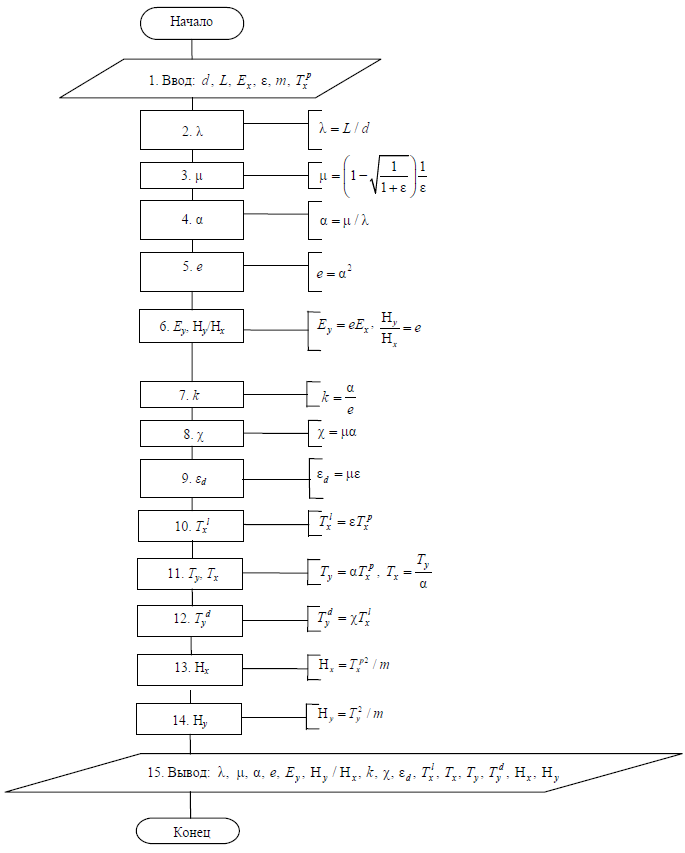
Рис. 3. Алгоритм расчета физико-механических свойств КВИ и ПШ (условие определенности)
Fig. 3. Algorithm for calculating the physical and mechanical properties
of cable and rope items and sennit cords (condition of certainty)
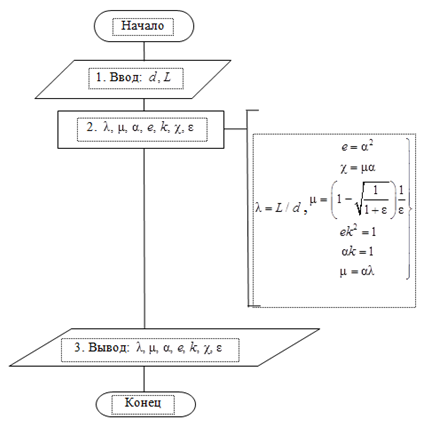
Рис. 4. Алгоритм расчета физико-механических свойств КВИ и ПШ (условие неопределенности)
Fig. 4. Algorithm for calculating the physical and mechanical properties of cable and rope items and sennit cords
(condition of uncertainty)
Результаты и обсуждение
Приведем расчет капроновых ниток и веревок на основании заданных экспериментальных характеристик при возможной статической и динамической нагрузке (табл.).
Заданные и расчетные физико-механические свойства капроновых ниток и веревок
(условие неопределенности)
Preset and calculated physical and mechanical properties of capron threads and ropes
(uncertainty condition)
|
Заданные |
Экспериментальные характеристики |
Расчетные |
Ошибка, % |
||||||||||
|
d, мм |
L, м |
Т, Н |
λ |
ε, % |
μ |
α, · 10–3 |
е, · 10–5 |
k |
χ, · 10–3 |
εр*, % |
μр** |
δε |
δμ |
|
0,45 |
0,1 |
9,80 |
222,2 |
7 |
0,72 |
2,2 |
50,0 |
447 |
1,1 |
7 |
0,5 |
0,0 |
30,6 |
|
19,61 |
11 |
1,27 |
2,2 |
49,8 |
447 |
1,1 |
11 |
0,5 |
0,0 |
60,6 |
|||
|
29,41 |
13 |
1,31 |
2,2 |
49,6 |
449 |
1,1 |
13 |
0,5 |
0,0 |
61,8 |
|||
|
0,56 |
19,61 |
178,6 |
4 |
3,32 |
2,7 |
73,9 |
368 |
1,3 |
4 |
0,48 |
0,0 |
85,5 |
|
|
36,22 |
9 |
2,07 |
2,6 |
68,8 |
381 |
1,2 |
9 |
0,47 |
0,0 |
77,3 |
|||
|
58,83 |
12 |
1,98 |
2,6 |
66,4 |
388 |
1,2 |
11,6 |
0,47 |
3,3 |
76,3 |
|||
|
0,85 |
19,61 |
117,6 |
6 |
2,93 |
4,0 |
1,6 |
246 |
1,9 |
6 |
0,48 |
0,0 |
83,6 |
|
|
58,83 |
11 |
1,92 |
3,9 |
1,5 |
254 |
1,8 |
11 |
0,46 |
0,0 |
76,0 |
|||
|
117,67 |
14 |
1,75 |
3,8 |
1,5 |
259 |
1,8 |
14 |
0,45 |
0,0 |
74,3 |
|||
|
1,1 |
39,22 |
90,9 |
4 |
1,97 |
5,3 |
2,8 |
187 |
2,5 |
4 |
0,48 |
0,0 |
75,6 |
|
|
58,83 |
5 |
1,94 |
5,3 |
2,8 |
188 |
2,5 |
5 |
0,48 |
0,0 |
75,2 |
|||
|
117,67 |
7 |
1,88 |
5,2 |
2,7 |
191 |
2,4 |
7,3 |
0,48 |
4,3 |
74,5 |
|||
* εр – расчетное значение относительного удлинения; ** μр – расчетное значение коэффициента Пуассона.
Воспользуемся алгоритмом, приведенным на рис. 4, используя экспериментальные данные [5].
Исходя из данных таблицы можно сделать следующие выводы:
– метод расчета физико-механических свойств капроновых ниток и веревок при условии неопределенности дает ошибку в расчете относительного удлинения δε не более 4,3 %, но при этом максимальная ошибка δμ в расчете коэффициента Пуассона μ достигает 85,5 %. Это доказывает, что формула (9) для расчета коэффициента Пуассона μ для анизотропных тел не позволяет оценить данный коэффициент при малых нагрузках T;
– для оценки и расчета коэффициента Пуассона μ необходимо получить аналитическую зависимость вида (10).
Отобразим графически расчетные данные таблицы, т. е. зависимости χ = f(λ) и α = f(λ) (рис. 5).
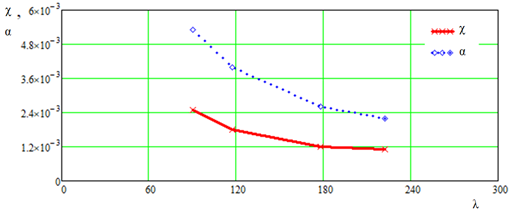
Рис. 5. Зависимости χ = f(λ) и α = f(λ)
Fig. 5. Dependencies χ = f(λ) and α = f(λ)
На рис. 5 видно, что с увеличением конструктивного удлинения параметры λ и χ уменьшаются по гиперболической зависимости.
Заключение
В статье приводятся алгоритмы расчета физико-механических свойств КВИ и ПШ при условии определенности (заданы параметры) и неопределенности (не заданы параметры). Рассчитаны физико-механические свойства капроновых ниток и веревок при условии неопределенности на основании заданных параметров при возможной статической и динамической нагрузке.
Производительность внешних продольных и поперечных сил, создаваемых при буксировке траловых систем, а именно сил натяжения и сжатия канатов, веревок и ниток канатно-сетного орудия промышленного рыболовства, связана с продольным модулем упругости и поперечным модулем упругости канатно-веревочного изделия.
На основании вышеприведенных формул (1)–(9), (12)–(14) и алгоритмов расчета зависимости физико-механических свойств КВИ и ПШ от действующей нагрузки в продольном сечении, связывающих конструктивные, геометрические и силовые их характеристики при условии V = const и m = const, в дальнейшем спрогнозируем физико-механические свойства КВИ и ПШ.
1. Nedostup A. A., Razhev A. O. Proizvoditel'nost' sil tralovoy sistemy: postanovka zadachi // Vestn. Astrahan. gos. tehn. un-ta. Ser.: Rybnoe hozyaystvo. 2021. № 2. S. 55-65.
2. Nedostup A. A., Razhev A. O., Nasenkov P. V., Ko-novalova K. V., Bykov A. A., Pivovarova Yu. S. Proizvoditel'nost' sil tralovoy sistemy - III: matematicheskoe modelirovanie (chast' I) // Vestn. Astrahan. gos. tehn. un-ta. Ser.: Rybnoe hozyaystvo. 2021. № 4. S. 63-72.
3. Rozenshteyn M. M. Proektirovanie orudiy rybo-lovstva. M.: Kolos, 2009. 400 s.
4. Gabryuk V. I., Kulagin V. D. Mehanika orudiy rybolovstva i ARM promyslovika. M.: Kolos, 2000. 416 s.
5. Nasenkov P. V., Nedostup A. A., Dolin G. M. Eksperimental'nye issledovaniya koefficienta Puassona nitevidnyh rybolovnyh materialov // Izv. Kaliningr. gos. tehn. un-ta. 2021. № 62. S. 26-34.
