Russian Federation
Russian Federation
UDC 398.1
UDC 53.08
An approach based on random fuzzy variables (RFV) is proposed for expressing measurement uncertainty. It differs from the approach adopted in the Guide to the Representation of Uncertainty in Measurement of the International Organization for Standardization (ISO), which is based on probability theory. First, a brief overview of the principles of RFV forming membership functions and their processing is given, as well as a description of the mathematical apparatus used. Then, using the example of a well-known method for measuring the resistance of a conductor on direct current, known as the ammeter and voltmeter method, various possibilities of constructing RFV based on a priori data on the measuring device and the conditions of the measurement experiment known to a metrologist are investigated. The purpose of this work is to show how RFV can be formed and used in a simple practical application based on the available metrological information. It is shown how the available information on the measuring devices used can be supplemented with various assumptions that do not contradict the real conditions of the measurements, which helps to construct RFV that adequately describe the resulting measurement uncertainty. Type A and B uncertainties are analyzed separately and their combined effect on the resulting uncertainty of the final measurement result is investigated. Finally, the RFV method is compared with the approach used in the ISO Guide, which demonstrates the ability of the proposed method, when correctly applied, to properly take into account the effects of different contributions to uncertainty.
random fuzzy variables, multimeter, standard, random variables, uncertainty estimation, Monte Carlo method
Введение
В нескольких относительно недавно опубликованных работах вместо традиционного подхода, рекомендованного Руководством по представлению неопределенности измерения (НИ) (IEC-ISO Guide to the Expression of Uncertainty in Measurement, GUM) [1–4], в основе которого лежит теория вероятностей, был предложен новый подход к оценке неопределенности измеряемой величины, базирующийся на нечетких и случайных нечетких переменных (СНП) [5–10]. В цитируемых работах показаны преимущества этого нового подхода, которые проявляются особенно рельефно, когда неслучайные эффекты вносят значительный вклад в неопределенность измерений [5, 6] или если имеются очень ограниченные знания о различных вкладах в неопределенность [9]. В частности, подход, основанный на использовании СНП, как представляется авторам, является максимально обобщенным, поскольку, с одной стороны, он основан на математической теории доказательств, которая как частные случаи включает в себя теории вероятности и возможностей [11], а, с другой стороны, учитывает совместное влияние случайных и неслучайных эффектов, влияющих на неопределенность измерения, в одном математическом объекте [5, 6, 11, 12]. До настоящего времени, несмотря на наличие хорошо проработанного математического аппарата для обработки СНП [6, 11, 12], в литературе известно лишь очень небольшое число его практических приложений, в основном связанных с конкретными процедурами измерения [13–16].
Цель статьи – показать, как работает метод СНП и как он может быть применен для оценки неопределенности с помощью простой, хотя и достаточно важной процедуры измерения, а именно измерения сопротивления на постоянном токе с использованием метода амперметра и вольтметра [17]. После краткого изложения теоретических основ метода СНП он применяется к выбранному тематическому исследованию. В частности, обсуждается правильное использование имеющихся фактических данных при построении СНП, а также представлены базирующиеся на различных допущениях результаты экспериментальных исследований, которые сравниваются с результатами, рассчитанными с помощью классических процедур, рекомендованных существующими стандартами [1–4].
Краткое описание подхода, основанного на случайных нечетких переменных
Подход, лежащий в основе метода СНП, состоит в представлении результата измерения в совокупности со связанной с ним неопределенностью измерения в терминах определенного вида нечеткой переменной типа 2, которая получила в литературе название случайно-нечеткой переменной [11, 12, 18]. В частности, было показано [11, 12], как СНП может быть определена в виде совокупности доверительных интервалов типа 2, являющихся его α-отрезками, имеющими следующее представление:
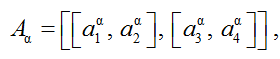, α ∈ [0, 1], (1)
которые подчиняются следующим ограничениям [11]:
Последовательности доверительных интервалов типа 
генерируют две функции принадлежности, которые являются нормальными и выпуклыми; 
из неравенства 
следует, что:
.
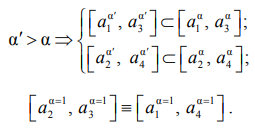Каждый α-отрезок представляет собой доверительный интервал, соответствующий доверительной вероятности p = 1− α [6, 11, 12]. На рис. 1 показаны примеры СНП.
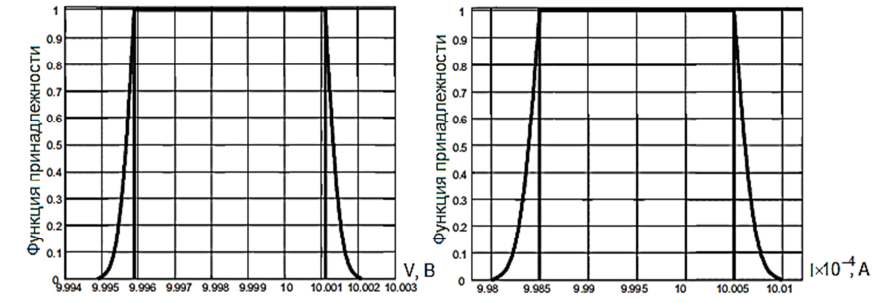
а б
Рис. 1. СНП для вольтметра (а) и амперметра (б), сформированные по опытным данным
Fig. 1. RFV for the voltmeter (а) and ammeter (б), generated from experimental data
В соответствии с определением доверительных интервалов типа 2 [11] нижняя и верхняя границы в каждом интервале (1) представлены в виде замкнутых интервалов 
. Ширину этих интервалов можно интерпретировать как вклады случайных факторов в неопределенность измерений [6, 11].
С другой стороны, внутренний интервал 
в выражении (1) является доверительным интервалом типа 1. Поэтому он может быть удобно связан с последствиями всех неслучайных вкладов в неопределенность измерений, таких как некомпенсированные систематические вклады или неопознанные вклады [5, 6, 11, 12].
Можно сделать вывод, что СНП, сформированная как полный набор доверительных интервалов типа 2 для всех возможных уровней значимости, может быть успешно использована для представления результата измерения вместе со связанной
с ним неопределенностью и для правильного учета различных эффектов, способствующих неопределенности измерения [5, 6, 11, 12]. Наличие подходящего математического аппарата для обработки СНП [11, 12] позволяет обрабатывать результаты измерений вместе со связанной с ними неопределенностью измерений [13].
Конечно, критическим моментом метода СНП является определение индивидуальных СНП всех факторов, вносящих вклад в результирующую неопределенность, на основе имеющейся метеорологической информации. Для генерации функций принадлежностей существуют различные математические подходы [8–10, 12], опирающиеся на имеющуюся информацию о процессе измерения, хотя до сих пор они не были ориентированы на формирование СНП в типичных условиях измерения.
В дальнейшем изложении авторы постарались восполнить этот пробел путем анализа того, как подход на основе СНП может быть применен для измерения на постоянном токе сопротивления проводника с помощью классического метода амперметра и вольтметра. В процессе изложения обсуждается методика построения СНП, когда в ее основу положены различные возможные предположения, которые формулируются на базе имеющейся ограниченной метрологической информации, имеющейся в распоряжении метролога.
Экспериментальная измерительная установка
Схема измерения. Классический метод амперметра и вольтметра (МАВ), используемый при измерении на постоянном токе сопротивления проводника [17], очень прост в реализации и требует минимальный состав измерительных приборов, на его примере наглядно демонстрируются некоторые важные и общие для различных измерительных систем проблемы, обусловленные тем, как можно использовать априорно доступные сведения о точности имеющихся приборов для построения СНП.
Для простоты изложения рассмотрим измерительную схему, используемую в МАВ для относительно больших величин измеряемых сопротивлений (рис. 2).
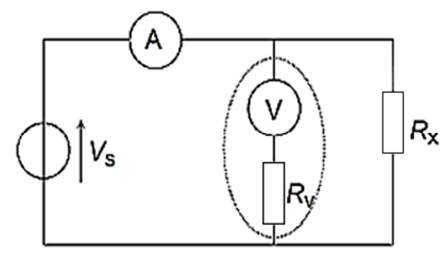
Рис. 2. Измерительная схема: А – амперметр; Vs – напряжение питания; Rx – измеряемое сопротивление;
RV – внутреннее сопротивление вольтметра V
Fig. 2. Measuring circuit: A – ammeter; Vs – supply voltage; Rx – measured resistance;
RV – voltmeter internal resistance V
С помощью такой схемы измеряется сопротивление резистора, имеющее номинальное значение Rx = 10 кОм. В качестве амперметра и вольтметра в схеме используются цифровые мультиметры Fluke 45 [19] (Fluke Corporation, США).
Сначала предположим, что вольтметр V имеет бесконечное внутреннее сопротивление RV = 
а сопротивление амперметра равно нулю. Тогда, если измерительная схема на рис. 2 питается напряжением Vs= 10 В на постоянном токе, то показания вольтметра будут Vm = Vs. При этом ток, текущий через амперметр A, будет равен Im = Vm / Rx = 1 мА. Следовательно, у цифровых мультиметров для вольтметра надо выбрать диапазон 10 В, а для амперметра – диапазон 10 мА.
Поскольку мультиметры Fluke 45 имеют конечное внутреннее сопротивление Rv = 10 МОм при измерении напряжения, следует применить соответствующую коррекцию. Тогда скорректированное измеренное значение Rxc измеряемого истинного сопротивления Rx будет равно [17]
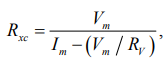(2)
где индекс m обозначает, что значения напряжения и тока были получены из показаний мультиметров Fluke 45.
Исследование спецификаций мультиметров. Технические характеристики точности мультиметров Fluke 45 в выбранных диапазонах, согласно спецификации производителя [19], следующие:
1. Точность измерения напряжения: 0,02 % от показаний прибора +6 dgt, где минимальное разрешение, соответствующее изменению показаний на единицу в младшем разряде дисплея прибора, равно 100 мкВ.
Следовательно, при измерении напряжения примерно 10 В получается интервал, равный ±2,6 мВ относительно измеренного значения.
2. Точность измерения тока: 0,05 % от показаний +5 dgt, где минимальное разрешение, соответствующее одной цифре в младшем разряде дисплея прибора, составляет 100 нА.
Это дает при измерении тока порядка 10 мА интервал, равный ±1 мкА относительно измеренного значения.
Производитель не предоставляет никаких спецификаций относительно точности, с которой определяется внутреннее сопротивление мультиметра, работающего в режиме вольтметра. Поскольку эти данные важны только при высокоточных измерениях, например при фактической калибровке какого-либо устройства, а в данном примере показываются только возможности метода СНП для определения неопределенности измерения, вполне естественно предполагать, что точность, с которой известно внутреннее сопротивления вольтметра, равна 1 · 10–6. Тогда интервал относительно измеренного значения RV получается равным ±10 Ом.
Применение метода СНП
Первый этап процедуры реализации метода СНП состоит в построении СНП, представляющих результаты измерений напряжения и тока. В теории доказательств [18, 20] показано, что для этого можно использовать всю имеющуюся на этот момент информацию об измерительных объектах и приборах. Как следствие, различные СНП могут быть построены, если в их основу положен специфический объем информации, что известна метрологу в момент проведения процедуры измерений.
В последующем изложении будут делаться различные допущения, предполагающие постепенное увеличение объема доступной информации, и для каждого отдельного случая будут построены соответствующие СНП, которые используются для нахождения результирующей СНП, связанной с измеренным значением Rx.
Сначала предположим, что показания вольтметра V составляют Vm = 9,9985 В, при этом он имеет бесконечное внутреннее сопротивление. Это точно соответствует спецификации точности из руководства по эксплуатации прибора производителя цифрового мультиметра Fluke 45, если подаваемое на вольтметр напряжение равно номинальному напряжению питания Vs = 10 В. В этом случае номинальный ток, протекающий через резистор Rx, измеряется амперметром A. Пусть он равен Im = 0,9995 мА, что полностью соответствует спецификации точности из того же руководства по эксплуатации, когда ток, протекающий через амперметр, равен номинальному току 1 мА.
Теперь усложним модель и будем считать, что мультиметр имеет реальное внутреннее сопротивление, когда он работает в режиме вольтметра. В этом случае вольтметр V выдает то же значение напряжения, что и раньше, но амперметр A измеряет суммарный ток, протекающий через измеряемое сопротивление Rx и внутреннее сопротивление мультиметра RV. Предположим, что новые показания амперметра Im = 1,0005 мА.
Если единственной доступной информацией является информация, предоставленная изготовителем [19], СНП, представляющие результаты измерения напряжения и тока, должны быть прямоугольными, с основаниями (совпадающими с их
α-отрезками для уровня значимости α = 0), равными соответственно интервалам 
мА в случае бесконечного внутреннего сопротивления мультиметра и в случае
его конечного внутреннего сопротивления 
мА. Это хорошо согласуется с представлением о ситуации полного незнания в рамках теории доказательств [6, 18, 20]. Фактически производитель измерительного прибора указывает только интервал, охватывающий измеряемое значение, предположительно в пределах которого должно оказаться значение измеряемой величины, но не дает никакой дополнительной информации о возможном местоположении этого значения внутри данного интервала. Согласно методу СНП, функция принадлежности (ФП), полученная на основе информации, предоставленной производителем, дает индивидуальные функции принадлежности СНП, представляющие результаты измерений вольтметром и амперметром.
Для цифровых мультиметров часто характерны ситуации, когда наличие аддитивных случайных факторов приводит к случайному изменению последних цифр на дисплее измерительного прибора. Как следствие, результат измерения обычно оказывается внутри интервала, ширина которого превосходит ширину интервала, полученного с помощью калибровочных данных. Это означает, что, если в течение некоторого интервала времени проводятся повторные измерения тока или напряжения, то результаты этих измерений являются нормально распределенными случайными величинами. Поэтому при оценке неопределенности типа А именно такое распределение следует принимать во внимание [2, 15, 16].
Чтобы также учесть эти случайные факторы, предполагалось, что в результате их действия результаты измерений будут являться случайными величинами, распределенными по нормальному закону с математическими ожиданиями, совпадающими с вышеуказанными предполагаемыми результатами измерений, и стандартными отклонениями σV = 0,33 мВ и σI = 0,33 мкА для измерений напряжения и тока соответственно. Применяя к этим распределениям преобразование вероятности-возможности, предложенное в работах [11, 21], получают внешние ФП СНП, представляющие результаты измерений напряжения и тока МВА.
Случайные нечеткие переменные, полученные при этих допущениях, показаны на рис. 1. Случайная нечеткая переменная, представляющая результат измерения тока, рассчитана в предположении о бесконечном внутреннем сопротивлении вольтметра. Если отказаться от этого предположения, будет получена СНП, сдвинутая вправо на 1 мкА. Что касается внутреннего сопротивления вольтметра, то оно представлено чисто нечеткой СНП,
с прямоугольной ФП, имеющей основание, равное интервалу: 
МОм. Выбор такой СНП обусловлен тем, что в наличии нет никакой информации, кроме нахождения фактического значения внутреннего сопротивления вольтметра в этом интервале.
Использование одного и того же прибора для измерений напряжения и тока. Теперь предположим, что один и тот же прибор используется как для измерения напряжения, так и для измерения тока. Это предположение вполне вероятно, поскольку мультиметры Fluke 45 дают возможность одновременного проведения измерений в двух каналах тока и напряжения [19]. С другой стороны, можно полагать, что ток и напряжение измеряются с помощью двух идентичных приборов, откалиброванных в одинаковых условиях. Это предположение совершенно эквивалентно предыдущей гипотезе и полностью соответствует ситуации, показанной на рис. 2. В соответствии с этими предположениями весьма маловероятно, что неслучайные факторы будут скомпенсированы, и поэтому СНП, показанные на рис. 1, могут быть пересчитаны в соответствии с законом Ома Rx = Vm / Im, если предполагается, что внутреннее сопротивление вольтметра бесконечно. Если же учитывается фактически конечное внутреннее сопротивление мультиметра, то для расчета сопротивления Rx надо пользоваться выражением (2).
Полученный результат измерения сопротивления Rx в терминах СНП показан на рис. 3.
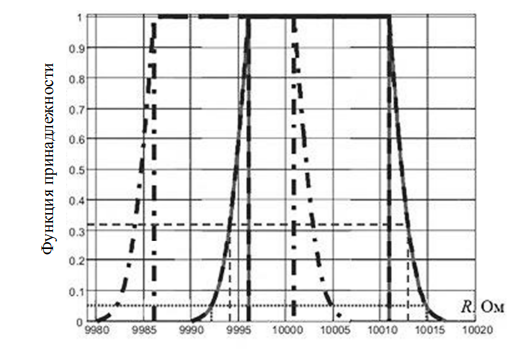
Рис. 3. СНП, представляющие измеренное значение Rx при условии использования абсолютно одинаковых мультиметров и отсутствия компенсации неслучайных эффектов: левая СНП (штрихпунктирная линия) – измеренное сопротивление без компенсации внутреннего сопротивления вольтметра; правая СНП (сплошная линия) – сопротивление, измеренное после проведения процедуры компенсации внутреннего сопротивления вольтметра
Fig. 3. RFVs representing the measured value of Rx under the condition of using absolutely identical multimeters
and no compensation for non-random effects: left RFV (dash-dotted line) is the measured resistance without compensation
for the internal resistance of the voltmeter; right RFV (solid line) is the resistance measured after the procedure
for compensating the internal resistance of the voltmeter
Если применяется упрощенный расчет по закону Ома без коррекции результата, то полученная СНП показана слева штрихпунктирной линией. Более правильный результат получается при использовании выражения (2), что дает СНП, расположенную справа (сплошная линия) (см. рис. 3). Безусловно, эти результаты полностью совместимы с СНП, полученной в предположении бесконечного внутреннего сопротивления мультиметра и совпадающей с объединением левой и правой СНП. Доверительные интервалы, соответствующие этим СНП для различных доверительных вероятностей, показаны в табл. 1 в строке «СНП».
Таблица 1
Table 1
Доверительные интервалы для доверительных вероятностей 0,95 и 0,68
в случае использования одинаковых мультиметров и без компенсации
Confidence intervals for confidence probabilities of 0.95 and 0.68
when using identical multimeters and without compensation
|
Метод |
Доверительный интервал, МОм |
|
|
Доверительная вероятность |
0,95 |
0,68 |
|
СНП |
[9 992,2; 10 014,8] |
[9 994,1; 10 012,9] |
|
Расчет распространения неопределенности |
[9 993,3; 10 013,7] |
[9 998,4; 10 008,6] |
|
Метод Монте-Карло |
[9 995,8; 10 012,2] |
[9 998,8; 10 009,2] |
Однако предположение о невозможности компенсации неслучайных эффектов может оказаться слишком пессимистичным, поскольку оно предполагает одинаковое функционирование внутренних цепей как вольтметра, так и амперметра. Это очень жесткое требование, т. к. даже если один и тот же прибор используется как для измерения напряжения, так и тока, внутренние преобразовательные блоки этих каналов различаются, по крайней мере, для интерфейсных цепей.
Если принять во внимание эту дополнительную информацию, то вполне возможна частичная компенсация и неслучайных эффектов. В этом случае внутренняя функция принадлежности СНП, представляющая результаты измерения напряжения и тока, принимает трапециевидную форму, чтобы учесть эту дополнительную информацию. Относительное уменьшение α-отрезка на уровне значимости α = 1 по сравнению с α-отрезком на уровне α = 0 зависит от того, насколько отличаются схемы внутренних каналов напряжения и тока прибора. В качестве примера здесь рассматривается разница в 10 %.
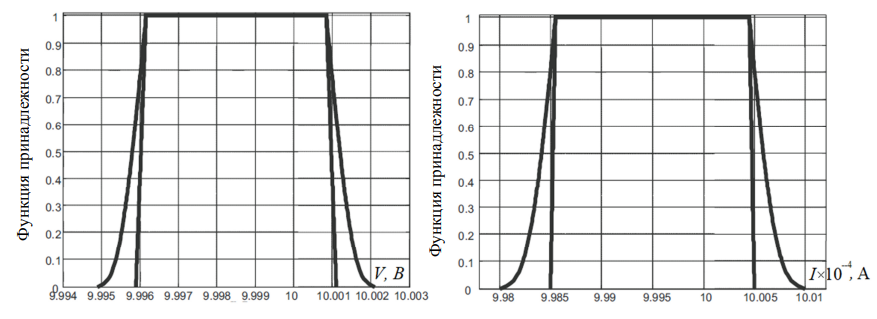
Если последнее предположение справедливо, то получаются СНП для измеренных значений напряжения и тока, которые показаны на рис. 4;
в этом случае относительно внутреннего сопротивления вольтметра могут использовать те же соображения, что и при построении рис. 1.
а б
Рис. 4. СНП результатов измерений вольтметра (а) и амперметра (б) в предположении частичной компенсации
Fig. 4. RFV of measurement results for the voltmeter (а) and ammeter (б) assuming partial compensation
Результаты измерений для Rx приведены на рис. 5, где две показанные СНП имеют тот же смысл, что и их аналоги, приведенные на рис. 3.
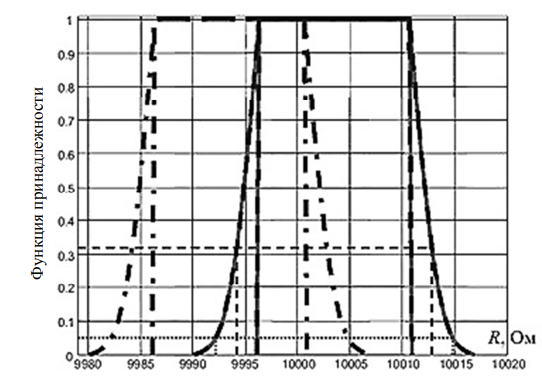
Рис. 5. СНП, представляющие измеренное значение Rx при условии использования абсолютно одинаковых мультиметров и наличия частичной компенсации неслучайных эффектов: левая СНП (штрихпунктирная линия) – измеренное сопротивление без компенсации внутреннего сопротивления вольтметра; правая СНП (сплошная линия) – сопротивление, измеренное после проведения процедуры компенсации внутреннего сопротивления вольтметра
Fig. 5. RFV representing the measured value of Rx under the condition of using absolutely identical multimeters
and the presence of partial compensation for non-random effects: the left RFV (dash-dotted line) is the measured resistance without compensation for the internal resistance of the voltmeter; the right RFV (solid line) is the resistance measured after the procedure for compensating the internal resistance of the voltmeter
Доверительные интервалы, соответствующие этим СНП для различных доверительных вероятностей, показаны в табл. 2 в строке «СНП».
Таблица 2
Table 2
Доверительные интервалы для доверительных вероятностей 0,95 и 0,68
при использовании одинаковых мультиметров с частичной компенсацией
Confidence intervals for confidence probabilities of 0.95 and 0.68
when using identical multimeters with partial compensation
|
Метод |
Доверительный интервал, МОм |
|
|
Доверительная вероятность |
0,95 |
0,68 |
|
СНП |
[9 992,2; 10 014,8] |
[9 994,2; 10 012,8] |
|
Расчет распространения неопределенности |
[9 992,9; 10 014,1] |
[9 998,2; 10 008,8] |
|
Метод Монте-Карло |
[9 995,9; 10 014,0] |
[9 999,6; 10 010,3] |
Сравнение с подходом из Руководства [1, 2]
и российских стандартов [3, 4]. На той же самой измерительной установке была подсчитана неопределенность измерения сопротивления Rx на основе подхода, предложенного в Руководстве [1, 2] и российском стандарте [3, 4]. Были рассмотрены как закон распространения неопределенности (РН) [2], так и подход на основе метода Монте-Карло, предложенный в Приложении 1 к Руководству [22] и его российском аналоге [23].
При оценке стандартной неопределенности результатов измерения напряжения и тока были сделаны следующие допущения:
– информация о калибровочных параметрах, предоставленная изготовителем, использовалась в качестве оценки неопределенности типа В, и предполагалось, что эти параметры распределены равномерно в выбранном интервале значений;
– оценка типа А строилась на основании неопределенности случайных факторов, когда они считались случайными величинами с нормальным распределением, у которых математические ожидания совпадают с измеренными их значениями и определены стандартные отклонения этих факторов. В качестве оценки неопределенности типа В для стандартной неопределенности была взята имеющаяся в наличии информация о точности измерения внутреннего сопротивления вольтметра, которая предполагалась распределенной равномерно на интервале, указанном в руководстве по эксплуатации прибора.
Когда расчет РН положен в основу определения стандартной неопределенности результатов измерения напряжения и тока, с использованием вкладов в нее обоих типов А и В вычисляется их общее среднеквадратичное значение. В отличие от такого метода вычисления, при использовании подхода, основанного на случайных экспериментах Монте-Карло [24], в каждом модельном эксперименте различные вклады в неопределенность задавались с помощью предполагаемых распределений вероятностей, а затем объединялись их суммарные эффекты от воздействия.
Стандартная неопределенность, связанная с ситуацией, изображенной на рис. 3, при оценивании ее методом Монте-Карло, вычислялась в предположении о единичном коэффициенте корреляции (ρ = 1) для вкладов типа B.
Использование подхода, основанного на расчете РН, позволило получить доверительные интервалы, указанные в табл. 1, соответствующие коэффициенту покрытия m = 2 (доверительная вероятность p = 0,95) и m = 1 (p = 0,68). В табл. 1 показаны также доверительные интервалы, предоставляемые методом Монте-Карло, когда ρ = 1 для вкладов типа B.
Стандартная неопределенность, связанная со случаем, рассмотренным на рис. 5, была оценена в предположении о коэффициенте корреляции ρ = 0,9 (применяется только к типу B при использовании метода Монте-Карло).
Доверительные интервалы, полученные с помощью моделирования методом Монте-Карло, показаны в табл. 2.
Продемонстрированные результаты хорошо согласуются с результатами, полученными с помощью подхода с СНП: подход РН обеспечивает более узкие интервалы, поскольку он всегда учитывает вероятностную компенсацию между различными вкладами в неопределенность; подход с использованием метода Монте-Карло обеспечивает более близкие результаты к методу СНП, поскольку он учитывает фактические распределения вероятностей.
Использование различных приборов для измерений напряжения и тока. Когда для измерения напряжения и тока используются два разных мультиметра, хотя, возможно, эти приборы одного типа, результаты измерений, предоставляемые обоими приборами, произведенными одним и тем же производителем, можно считать случайными величинами, распределенными с одинаковой плотностью вероятности. Следовательно, если закон распределения у этих результатов измерения равномерный, то вероятно, что произойдет компенсация между измерениями напряжения и тока.
Чтобы учесть подобную дополнительную информацию в СНП, представляющих результаты измерения напряжения и тока, равномерное распределение вероятностей должно быть преобразовано в соответствующее распределение возможностей [11, 21], и полученное распределение должно использоваться в качестве внутренней ФП желаемых СНП. Согласно [11], в этом случае получается треугольная внутренняя ФП. В предположении, что в измерительной системе по-прежнему действуют те же случайные факторы, СНП, задающие измеренные значения напряжения и тока, становятся такими, как показано на рис. 6.
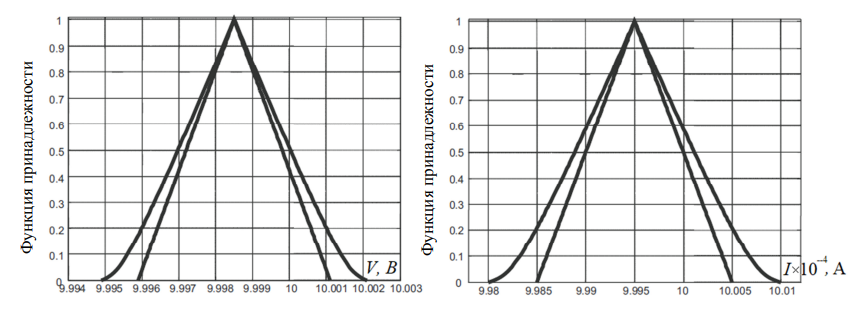
а б
Рис. 6. Результаты измерений вольтметра (а) и амперметра (б)
в предположении использования различных мультиметров для измерения напряжения и тока
Fig. 6. Measurement results for the voltmeter (а) and ammeter (б)
assuming the use of different multimeters for voltage and current measurements
Результаты измерений для данных СНП приведены на рис. 7, где различные СНП имеют то же значение, что и те, что показаны на рис. 3.
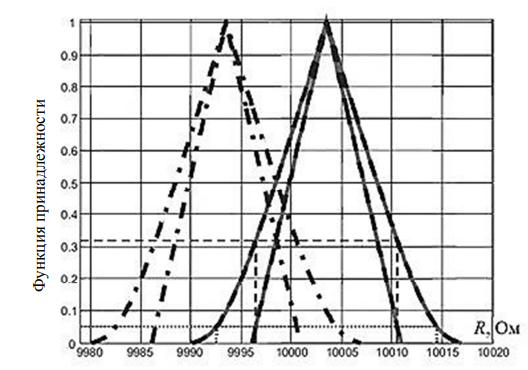
Рис. 7. СНП, представляющие измеренное значение Rx в предположении различных мультиметров для напряжения
и тока: левая СНП (штрихпунктирная линия) – измеренное сопротивление без компенсации внутреннего сопротивления вольтметра; правая СНП (сплошная линия) – измеренное сопротивление после компенсации внутреннего сопротивления вольтметра
Fig. 7. RFV representing the measured value of Rx assuming different multimeters for voltage and current:
left RFV (dash-dotted line) – measured resistance without compensation for the internal resistance of the voltmeter;
right RFV (solid line) – measured resistance after compensation for the internal resistance of the voltmeter
Получены доверительные интервалы (табл. 3).
Таблица 3
Table 3
Доверительные интервалы для доверительных вероятностей
0,95 и 0,68 при использовании различных мультиметров для напряжения и тока
Confidence intervals for confidence probabilities
0.95 and 0.68 when using different multimeters for voltage and current
|
Метод |
Доверительный интервал, МОм |
|
|
Доверительная вероятность |
0,95 |
0,68 |
|
СНП |
[9 992,2; 10 014,5] |
[9 996,5; 10 010,5] |
|
Расчет распространения неопределенности |
[9 989,8; 10 017,2] |
[9 996,7; 10 010,3] |
|
Метод Монте-Карло |
[9 993,0; 10 015,4] |
[9 997,2; 10 011,1] |
Сравнение с подходом из Руководства [1, 2]
и российских стандартов [3, 4]. Подход, принятый Руководством [1, 2] и российским стандартом [3, 4], был вновь рассмотрен в соответствии с теми же допущениями, что и в предыдущем подразделе. Использование двух различных приборов для измерения напряжения и тока выражается в отсутствии какой-либо корреляции между проведенными ими измерениями напряжения и тока.
Стандартная неопределенность, связанная со случаем, рассмотренным на рис. 7, была оценена в предположении о нулевом коэффициенте корреляции ρ = 0. Применение расчета РН и моделирования методом Монте-Карло обеспечивает доверительные интервалы (см. табл. 3).
Как и ожидалось, результаты, полученные с помощью метода Монте-Карло, полностью согласуются с результатами, достигнутыми с помощью подхода СНП, поскольку в этом случае, вероятно, произойдет компенсация между вкладами различных факторов в неопределенности. С другой стороны, результаты, полученные на основе метода РН, несколько завышены, особенно когда выбираются низкие уровни доверительной вероятности, из-за принятых упрощений, сделанных относительно распределения вероятностей окончательного результата измерения.
Заключение
Обсуждался способ применения метода СНП к простой, хотя и значимой процедуре измерения, а также способ построения СНП в соответствии с имеющейся информацией. Было показано, как различные возможные метрологические предположения и допущения могут изменять форму получающихся СНП и оказывать значительное влияние на точность оценки конечного результата измерения.
Метод СНП был сравнен с подходом, применяемым в Руководстве [1, 2], что показывает способность метода СНП, при правильном применении, должным образом учитывать эффекты различных вкладов в неопределенность.
Результаты, полученные этим методом, хорошо согласуются с результатами, полученными при применении Приложения 1 к Руководству [22], а также его российском аналоге [23], и требуют гораздо меньших вычислительных усилий. Обнаружено меньшее согласие с результатами, полученными методом из Руководства [22], из-за упрощенных допущений, рассмотренных в самом стандарте [2].
1. BIPM, IEC, IFCC, ISO, IUPAC, IUPAP, and OIML. Guide to the Expression of Uncertainty in Measurement. Geneva, ISO, 1995. 118 p.
2. ISO/IEC GUIDE 98-3:2008. Uncertainty of Meas-urement – Part 3: Guide to the Expression of Uncertainty in Measure-ment. Geneva, ISO, 2010. 120 p.
3. GOST R 54500.1-2011 / Rukovodstvo ISO/MEK 98-3:2008. Neopredelennost' izmereniya. Chast' 3. Rukovodstvo po vyrazheniyu neopredelennosti izmereniya [ISS R 54500.1-2011 / ISO/IEC Guide 98-3:2008. Uncertainty of measurement. Part 3. Guidance on the expression of uncertainty in measurement]. Moscow, Standartinform Publ., 2011. 57 p.
4. GOST R 34100.1-2017 / ISO/IEC Guide 98-1:2009. Neopredelennost' izmereniya. Chast' 1. Vvedenie v rukovodstva po vyrazheniyu neopredelennosti izmereniya [ISS R 34100.1-2017 / ISO/IEC Guide 98-1:2009. Uncertainty of measurement. Part 1. Introduction to guides on the expression of uncertainty in measurement]. Moscow, Standartinform Publ., 2018. 22 p.
5. Ferrero A., Salicone S. The Random-Fuzzy Variables: A New Approach for the Expression of Uncertainty in Measure-ment. IEEE Trans. on Instrumentation and Measurement, 2004, vol. 53, no. 5, pp. 1370-1377.
6. Sharonov P. A., Umnova E. G., Vagarina N. S., L’vov A. A., Svetlov M. S. Al'ternativnyj podhod k vyra-zheniyu neopredelennosti izmereniya v eksperimente [An alternative approach to expressing measurement uncertainty in an experiment]. Matematicheskoe modelirovanie, komp'yuternyj i naturnyj eksperiment v estestvennyh naukah, 2021, no. 3. Available at: mathmod.esrae.ru/35-130 (accessed: 22.04.2025). DOI:https://doi.org/10.24412/2541-9269-2021-3-10-26.
7. Mauris G., Berrah L., Foulloy L., Haurat A. Fuzzy Handling of Measurement Errors in Instrumentation. IEEE Trans. on Instrumentation and Measurement, 2000, vol. 49, no. 1, pp. 89-93. DOI:https://doi.org/10.1109/19.836316.
8. Mauris G., Lasserre V., Foulloy L. A Fuzzy Approach for the Expression of Uncertainty in Measurement. Measurement, 2001, vol. 29, no. 3, pp. 165-177.
9. Mauris G. Expression of Measurement Uncertainty in a Very Limited Knowledge Context: A Possibility Theory-Based Approach. Trans. on Instrumentation and Measurement, 2007, vol. 56, no. 3, pp. 731-735. DOI:https://doi.org/10.1109/TIM.2007.894918.
10. Mencattini A., Salmeri M., Lojacono R. Type-2 Fuzzy Sets for Modeling Uncertainty in Measurement. Proc. of the 2006 IEEE Int. Workshop on Advanced Methods for Uncertainty Estimation in Measurement. Sardinia, Italy, IEEE, 2006. Pp. 8-13. DOI:https://doi.org/10.1109/AMYEM.2006.1650738.
11. Salicone S. Measurement Uncertainty: An Approach via the Mathematical Theory of Evidence. New York, Springer, 2007. 228 p.
12. Sparonov P. A. Onlajn-ocenka neopredelennosti izmeritel'nyh priborov s cifrovoj obrabotkoj signalov s pomoshch'yu nechetkih sluchajnyh peremennyh [Online uncertainty estimation of digital signal processing measuring instruments using fuzzy random variables]. Nadezhnost' i kachestvo: sbornik trudov Mezhdunarodnogo simpoziuma: v 2 tomah. Penza, Izd-vo PGU, 2024. Vol. 1. Pp. 436-443.
13. Zhu Q., Jiang Z., Zhao Z., Wang H. Uncertainty Estimation in Measurement of Micromechanical Properties Using Random-Fuzzy Variables. Review of Scientific In-struments, 2006, vol. 77, no. 3, art. 035107. DOI:https://doi.org/10.1063/1.2179408.
14. Salicone S., Tinarelli R. An Experimental Compari-son in the Uncertainty Estimation Affecting Wavelet-Based Signal Analysis by Means of the IEC-ISO Guide and the Random-Fuzzy Approaches. IEEE Trans. on Instrumentation and Measurement, 2006, vol. 55, no. 3, pp. 691-699. DOI:https://doi.org/10.1109/AMUEM.2005.1594603.
15. Solopekina A. A., L'vov A. A., Semezhev N. Calculation of Measurement Uncertainties of Multi-Port Transmission Line Reflectometer. Proc. 2014 Int. Conf. on Actual Problems of Electron Devices Engineering. Saratov, Russia, IEEE, 2014. Pp. 356-362. DOI:https://doi.org/10.1109/APEDE.2014.6958776.
16. Solopekina A. A., Semezhev N., L’vov A. A., Komarov V. V., Svetlov M. S. Application of the Uncertainty Method for Analysis of Multi-Port Correlator Accuracy. Proc. 2017 IEEE Russia Section Young Researchers in Electrical and Electronic Engineering Conf. Saint Petersburg, Russia, IEEE, 2017. Pp. 505-509. DOI:https://doi.org/10.1109/EIConRus.2017.7910664.
17. Panfilov V. A. Elektricheskie izmereniya [Electrical measurements]. Moscow, Akademiya Publ., 2013. 288 p.
18. Fluke 45 Dual display Multimeter – Service manual, Rev. 1, 1/04. 1999. 184 p.
19. Shafer G. A Mathematical Theory of Evidence. New Jersey, Princeton Univ. Press, 1976. 300 p.
20. Zadeh L. A. Fuzzy Logic and Approximate Reasoning. Synthese, 1975, vol. 30, no. 1, pp. 407-428.
21. Dhar M. Probability-Possibility Transformations: A Brief Revisit. Annals of Fuzzy Mathematics and Informat-ics, 2013, vol. 5, no. 2, pp. 301-308.
22. IEC-ISO, Guide to the Expression of Uncertainty in Measurement, Supplement 1, Numerical Methods for the Propagation of Distributions, 2004. 98 p.
23. GOST 34100.3.1-2017 / ISO/IEC Guide 98-3/Suppl 1:2008. Neopredelennost' izmereniya. Chast' 3. Rukovodstvo po vyrazheniyu neopredelennosti izmereniya. Dopolnenie 1. Transformirovanie raspredelenij s ispol'zovaniem metoda Monte-Karlo [ISS 34100.3.1-2017 / ISO/IEC Guide 98-3/Suppl 1:2008. Uncertainty of measurement. Part 3. Guidance on the expression of uncertainty in measurement. Supplement 1. Transformation of distributions using the Monte Carlo method]. Moscow, Standartinform Publ., 2018. 84 p.
24. Mashkin V. A., L'vov A. A. Vysokotochnye izme-reniya peremennogo toka, osnovannye na primenenii metoda Monte-Karlo [High-precision AC current measurements based on the Monte Carlo method]. Vestnik Saratovskogo gosudarstvennogo tekhnicheskogo universiteta, 2009, no. 4 (43), pp. 41-45.
