Россия
Россия
На основе аппарата регенерирующих процессов проводится анализ модели, описывающей процесс злонамеренных атак на защищаемый объект критической информационной инфраструктуры (КИИ). Предполагается: интервалы между последовательными моментами подготовки и реализации злоумышленных атак независимы в совокупности. Эти интервалы применительно к каждому из источников атак достаточно велики, источники между собой не общаются. Вероятность успешной атаки от одного источника достаточно мала, поэтому моменты успешной атаки для каждого из источников атак достаточно далеко удалены друг от друга. Как следствие, событие, связанное с успешным для злоумышленника завершением атаки, представляет собой редкое событие. Однако ввиду того, что успешная атака на объект КИИ порождает большие потери и издержки, возникает необходимость изучения рассматриваемого процесса. Основной исследуемой характеристикой в рамках описанной модели является первый (ближайший) момент успешного совершения злоумышленной атаки. Данная характеристика относится к числу наиболее важных для процесса противодействия атакам. Числовые оценки параметров момента совершения первой успешной атаки позволят более адаптивно организовать процесс противодействия атакам, осуществив на наиболее опасных и уязвимых интервалах времени дополнительные меры по обеспечению информационной безопасности. Анализ этой характеристики вы-полнен в условиях наличия неоднородности поведения всего процесса противостояния атак и противодей-ствия им. Предполагается, что интервалы между последовательными моментами атак и вероятности успешности атак во времени изменяются по степенному закону в среднем. Это предположение отражает процесс динамического изменения в источниках атак и в системе защиты объекта КИИ. Выведено асимптотическое соотношение для нормированной величины момента совершения первой атаки в условиях, когда интервалы между последовательными моментами совершения атак неограниченно растут, но при этом и число источников атак увеличивается так, что средняя доля успешных атак стремится к некоторому ненулевому пределу. Получены асимптотические выражения для среднего времени до ближайшей атаки.
информационная безопасность, объект критической инфраструктуры, первая успешная атака, неоднородный регенерирующий процесс, редкое событие, асимптотическое поведение, степенное из-менение во времени
Введение
В настоящее время объекты ключевой информационной инфраструктуры (КИИ) в России подвергаются интенсивным атакам на всех уровнях: физическом, информационном, военно-диверсионном
и др., поэтому задача повышения их надежности и защищенности является актуальной. Ввиду высокой защищенности объектов КИИ вероятность совершения злонамеренной успешной атаки крайне мала, но возможный ущерб может быть очень большим, т. е. риски в сфере обеспечения информационной безопасности (ИБ) в результате достаточно значимы, поэтому целесообразно их оценить. Ключевой характеристикой, необходимой для оценки рисков, является совокупная вероятность успешности злонамеренной атаки. Именно эта характеристика и рассматривается в работе. Ввиду малой величины вероятностей и редкости успешных атак для изучения указанных вероятностей предлагается использовать аппарат редких регенерирующих процессов [1–3]. В данной работе рассматривается задача оценки вероятностей возможных атак на объекты КИИ во времени. Опишем рассматриваемую модель более детально.
Модель противоборства злоумышленным атакам
Процесс совершения атак на объект защиты достаточно адекватно описывается восстанавливаемыми системами с очень малой вероятностью происшествия некоторого редкого события. В рамках данной работы таковым является совершение успешной для злоумышленника атаки на объект защиты, примеры приведены в [1–3]. С точки зрения противодействия атакам на объект защиты наибольший интерес представляет ближайший, начиная с данного, момент успешной атаки злоумышленника. Знание этой характеристики позволит более адекватно и своевременно предпринимать меры по противодействию атаке. Применительно к введенной модели на основе регенерирующих процессов данная характеристика описывает момент первого наступления некоторого (редкого) события [2].
В настоящее время для однородных регенерирующих процессов успешно реализован подход, опирающийся на результат А. Д. Соловьева [3]. Однако применительно к процессам обеспечения ИБ условие однородности, как правило, не выполняется. Это связано, прежде всего, с тем, что злоумышленный источник активно, агрессивно ищет новые возможности для проникновения на объект защиты и к защищаемым ресурсам, постоянно совершенствуя и изменяя свои методы и приемы злоумышленного проникновения. Поэтому необходимо обобщить результаты работ по однородным процессам на случай неоднородных регенерирующих процессов. Подобный результат для случая неоднородных процессов был ранее получен в работе [4]. Указанный ниже результат уточняется для важного частного случая, когда характеристики процесса противодействия с течением времени изменяются достаточно регулярным (степенным) образом. Данное предположение вполне приемлемо для сферы ИБ, поскольку в этой сфере резкие революционные изменения в средствах атак и методах противодействия практически не происходят, идет непрерывное устойчивое развитие возможностей как атак, так и средств противодействия им.
Таким образом, работа посвящена получению асимптотической оценки для момента времени совершения первой успешной для злоумышленника атаки на информационные ресурсы объекта защиты, относящегося к объектам КИИ. Предлагаемое решение опирается на методы анализа неоднородных регенерирующих процессов. Работ по неоднородным регенерирующим процессам применительно к данной сфере в доступной литературе найти не удалось. По общей теории однородных регенерирующих процессов достаточно полный обзор приведен в [2]. Работ по использованию аппарата регенерирующих процессов в сфере ИБ найти не удалось, за исключением работ с участием одного из авторов [4–6]. В данной работе основной теоретический результат работы [4] доказывается для случая степенного изменения во времени основных характеристик модели. Представляет интерес работа [7], также отсылающая к исследованию описанной характеристики.
Формализация задачи и предварительные сведения
Для формализации описанной выше задачи приведем вначале ограничения и условия, которые обеспечивают определенную асимптотическую согласованность основных характеристик модели [4].
Пусть задан регенерирующий процесс k(t) с точками регенерации t0 = 0 < t1 < t2 < ... < tn < ...; положим 
. Далее, на промежутке [tn–1, tn) в некоторый момент tn–1 + ηn (0 £ ηn < xn) возможно возникновение события An, представляющего собой успешную для злоумышленника завершившуюся атаку на информационные ресурсы объекта защиты. Предполагается, что событие An
и промежуток времени hn не зависят от значений процесса k(t) вне промежутка [tn–1, tn). Через ck обозначим индикатор события Ak: 
, когда событие Ak происходит, и 
, если не происходит. Основной изучаемой характеристикой является момент tn первого после tn–1 происшествия одного из событий Ak (k ³ n), т. е. успешной для злоумышленника реализации злонамеренной атаки, 
. Введем обозначения (n ³ 1; z ³ 0):
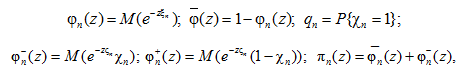
где M – знак математического ожидания. Отметим, что 
.
В работе изучается асимптотическое поведение момента tn в условиях, когда число источников атак растет, но сами атаки становятся более редкими. Указанное положение формализуется путем введения некоторого малого параметра, и чем меньше значение этого параметра, тем меньше значение уменьшения вероятностей редких событий. Таким образом, все перечисленные выше характеристики зависят также от некоторой переменной (параметра) : 
, где – множество допустимых значений переменной γ, представляющее собой интервал или дискретное множество на числовой оси, причем точка 0 есть предельная точка этого множества, поэтому запись «γ → 0» ниже равносильна условию: γ → 0 так, что
.
Для формулировки и доказательства основных утверждений работы воспользуемся условиями на введенные характеристики, которые сформулированы в [4]. Для обеспечения асимптотической сходимости введенных регенерирующих процессов необходимо потребовать определенную регулярность поведения основных характеристик системы. Данное требование в работе охвачено условиями А и Д, приводимыми ниже.
А. Существуют нормирующие функции 
) и для произвольного n ³ 1, z > 0 выполнено соотношение
(1)
Отметим, что функции 
описывают скорость стремления к нулю длительностей промежутков между последовательными моментами совершения атак.
Требование исчезающей редкости злоумышленных действий сформулировано в условии Б; количество точек регенерации на конечном промежутке и, соответственно, попыток злоумышленных действий согласованы в условии В. При этом рост числа интервалов и количества злоумышленных попыток также должны быть синхронизированы для обеспечения определенной регулярности поведения всей модели – условие Г.
Б. Справедливо соотношение 
.
Прежде чем описывать остальные условия, введем обозначения n £ 1, z > 0:
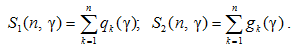
С целью упрощения изложения материала ниже, наряду с обозначением Si(n, g), используется также обозначение Si(n).
В. Для любых γ > 0 и целых n > 0 справедливы соотношения
, (2)
где 
– медленно меняющаяся функция, 
.
При этом справедливы соотношения [4]
(3)
Соотношение (2) и определяет степень регулярности изменения основных характеристик модели в схеме серий, в рамках которой доказывается основной результат. Соотношения (2) и (3) гарантируют существование функций λ1(γ) и λ2(γ) таких, что при согласованном изменении n и γ (напомним, рассматривается схема серий) конечен предел.
Необходимо 
i = 1,2.
Положим
Г. Существует предел:
(4)
То есть поведения процессов совершения атак и противоборства им асимптотически синхронизированы.
Д. При произвольном фиксированном значении переменной x > 0 соотношение (1) справедливо равномерно по всем n £ xl(g):
(5)
Е. Равномерно по k и n £ xl(g), где a и b (0 < a < < b < +¥) – произвольные числа, для любого T ³ 1 имеют место соотношения
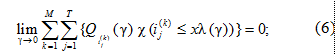
где Qn(g) = gn(g) + qn(g) (n ³ 1), при ïNkï < +¥ полагаем Qn(g) = 0 для n > ïNkï; c(A) есть индикатор события A; множества Nk вводятся в [4] и представляют собой разбиение множества всех источников атак на группы однородных.
Требование выполнения соотношения (6) равносильно следующему условию: для любого T ³ 1 равномерно по k (1 £ k £ M) и xÎ(a, b), где a и b (0 < a < b < ¥) – любые числа, существуют пределы:
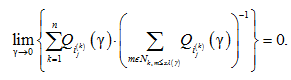(8)
Асимптотическое поведение момента совершения первой успешной атаки
Как было указано выше, момент наступления первой успешной злоумышленной атаки в рамках введенной модели совпадает с моментом первого наступления редкого события, поэтому ниже основной результат формулируется на языке редких событий. Предварительно введем некоторые обозначения:
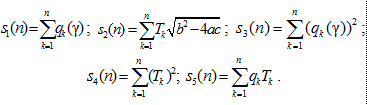
В работе [6] был выведен следующий результат.
Утверждение 1. Пусть выполнены условия A–E. Тогда существует предел:
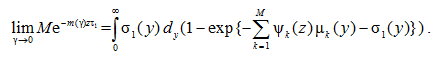(9)
Ниже соотношение (9) и используется для получения основного результата работы.
Утверждение 2. Предположим, что выполнены следующие условия:
а) для любого k ≥ 1существует Mξk Tk = Tk(γ), и для любых γ > 0 и n > 0 справедливы соотношения 
, где θi ≥ 0, Li(n) – медленно меняющиеся функции при n → ∞, 
и пусть λ(γ) есть функция такая, что 
;
б) для любого x ≥ 0 равномерно по n ≥ 1 существует предел
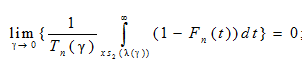(10)
в) для любого x ≥ 0 равномерно по n ≥ 1 справедливо
Тогда существует предел (z ≥ 0):
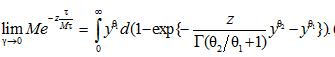(11)
При этом среднее время до первого отказа (до первой успешной злоумышленной атаки) равно
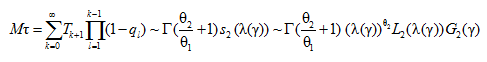(12)
при γ → 0 и 
. Здесь Г(х) – гамма-функция Эйлера.
В частности, если 
, то предельное распределение в (11) представляет собой показательное распределение с параметром 1.
Докажем утверждение 2. Условие Б утверждения 1 следует из условия в) утверждения 2 (см. (10)).
Из определения функции λ(γ) следует:
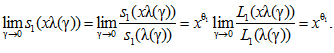(13)
Пусть функция m(γ) такова, что выполнено условие
(14)
Отметим, что условие (14) допускает определенную многозначность выбора функции m(γ), что приемлемо при выводе асимптотических соотношений.
Тогда для любого u > 0
,
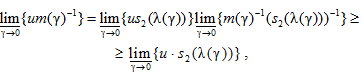откуда, ввиду (10), следует: для любого x > 0 равномерно по n ≥ 1
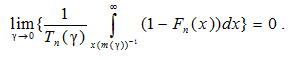. (15)
Полагая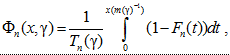 
, на основе (15) заключаем, что совокупность (по γ) вероятностных мер Φn(x, γ) при γ → 0 равномерно по
n сходится в собственном смысле к вероятностной мере, сосредоточенной в нуле. Отсюда, в силу замечания 2 [8, с. 317], следует, что для любого z > 0 равномерно по n ≥ 1 существует предел
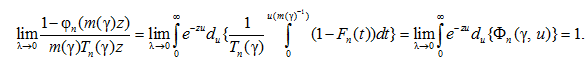(16)
Соотношение (16) совпадает с соотношением (1), т. е. выполнено условие А с gn(ω) = m(γ)Tn(γ),
ωn(z) = z (n ≥ 1). Далее, поскольку 
где 
имеем:
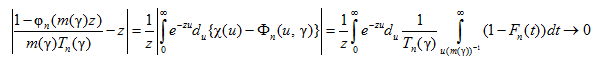(17)
при γ → 0 равномерно по n ≥ 1 ввиду условия (15). Следовательно, выполнено условие Д (см. (5)). Таким образом, при выполнении условия (13) имеют место условия А и Д.
Ввиду леммы 2 [4] выполняется соотношение
с M = 1 и ψk(z) = z, т. к. ωn(z) = z для всех n ≥ 1.
Покажем, что условие (4) выполнено при 
. Подсчитаем Mτ. Из (15) [6] имеем:
.
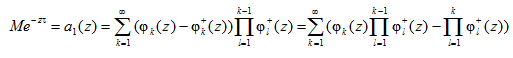Отсюда после замены переменной m = k – 1 аналогично (16) [6] получаем:
,
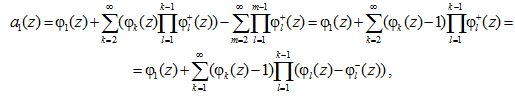откуда следует:
.
Так как 
, то первая часть соотношений (12) утверждения 2 доказана.
Из равенства (12) получаем:
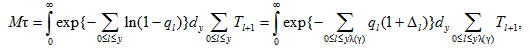
где 
при γ → 0 ввиду условия в) утверждения 2. Отсюда следует: при γ → 0
.
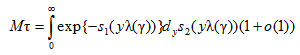Поскольку для i = 1,2 ввиду условия а) утверждения 2 при фиксированном γ > 0 и y → ∞ выполнено 
, то в силу условия а) утверждения 2 имеем:
.
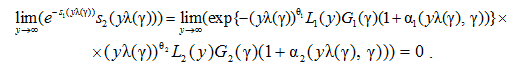Воспользовавшись последним соотношением в последнем интегральном соотношении для 
и проведя интегрирование по частям, приходим к асимптотическому соотношению:
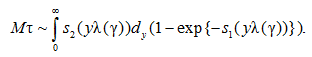
На основе общего представления медленно меняющихся функций [9, с. 323], заключаем: при любом выбранном δ > 0 можно выбрать постоянную величину γ1 > 0 такую, что выполнено 
при любом ν ≥ 1. Поэтому справедливо
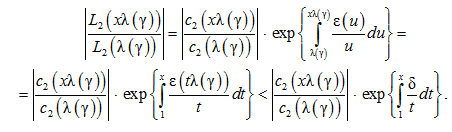
Таким образом, при любых γ > γ1 и x ≥ 1 выполнено соотношение
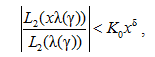
([9, с. 323])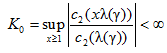 
. Так как 
при x ≤ 1, то из последнего соотношения получаем:
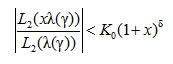
для всех x > 0 и γ > γ1.
Далее, совокупность вероятностных мер (по γ) 
при γ → 0 сходится в собственном смысле к вероятностной мере 
и, следовательно, в силу замечания 2 [8, с. 317], выводим: при γ → 0 выполнено
,
откуда следует асимптотическое соотношение (12).
Так как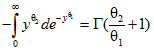 
, то из последнего соотношения получаем:
,
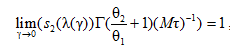откуда выводим справедливость (13) с
.
Таким образом, условия А и Д имеют место при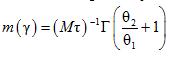 
.
Из условия а) утверждения 2 выводим:
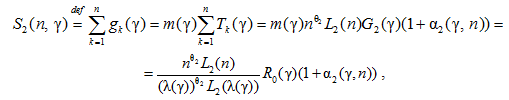, (18)
где 
. Поскольку (см. (17)) 
, то из условия а) утверждения 2 очевидно следует, что 
, и, в силу (18), получаем:
. (19)
Выполнение условия В при i = 1 следует из условия а) утверждения 2, т. к. 
. При i = 2 справедливость условия В следует из (18). Из условия а) утверждения 2 следует ; из (18) также следует
. Отсюда вытекает 
, и, следовательно, выполнено условие Г.
Наконец, для проверки выполнения условия Е отметим, прежде всего, что число различных групп M = 1, т. к. ωn(z) = z для всех n ≥ 1. Поэтому условие (8) равносильно условию: для любого T ≥ 1
,
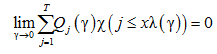которое вытекает из условий 
для всех i ≥ 1.
Условие (7) равносильно условию 
.
Так как 
, то последнее соотношение следует из (19). При этом 
.
Таким образом, мы доказали справедливость условий А–Е. При этом M = 1, 
. Отсюда, в силу следствия 1 [6], следует соотношение:
.
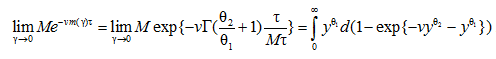Из последнего соотношения после замены переменной 
следует соотношение (11).
В частном случае 
и 
Отсюда после замены переменной
выводим:
.
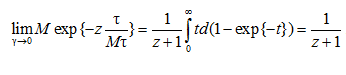Утверждение 2 доказано.
Таким образом, мы получили асимптотическое распределение (см. (11)) момента ближайшей атаки. Полученное распределение позволяет найти среднее время ожидания до момента ближайшей атаки, построить доверительные интервалы для разных уровней значимости, оценить вероятность злоумышленной атаки на конкретном временном интервале. Все перечисленные характеристики позволяют более адекватно реагировать на возможные атаки, предприняв, ввиду важности объекта, дополнительные усилия по повышению защиты информации на интервалах времени, где указанные характеристики указывают на повышенную вероятность злоумышленной атаки при степенном изменении интенсивности атак во времени.
Заключение
Полученный в работе результат показывает, что при весьма общих ограничениях на поведение исходных характеристик системы момент ближайшей злонамеренной атаки асимптотически сходится
к некоторому из распределений из двухпараметрического класса, описываемого преобразованием Лапласа – Стилтьеса (11). Необходимо исследовать особенности поведения соответствующей функции распределения, что предполагается выполнить в последующих работах. Более того, при некоторых естественных дополнительных ограничениях, охватывающих практически большинство ситуаций применимости утверждения 1, предельное распределение оказывается экспоненциальным. Таким образом, при «разумных» ограничениях поведение момента ближайшей злонамеренной атаки при достаточно большом числе источников атак с высокой степенью точности подчиняется экспоненциальному закону. Отметим следующие важные особенности этого закона:
1) экспоненциальный закон обладает свойством «отсутствия памяти», т. е. время ожидания атаки, начиная с текущего момента, никак не зависит от времени ожидания этой атаки;
2) среднее значение экспоненциального закона и среднее отклонение совпадают, т. е. поток экспоненциально распределенных событий (атак) ведет себя крайне нестабильно, принимая то очень малые значения, то очень большие.
Указанные особенности потока злонамеренных атак порождают нередко «эффект неожиданности» в системе обеспечения ИБ и требуют принятия мер по поддержанию ее непрерывно в полной готовности
1. Гнеденко Д. Б., Соловьев А. Д. Одна общая модель резервирования с восстановлением // Изв. АН СССР. Техн. кибернетика. 1974. № 6. С. 113–119.
2. Гнеденко Д. Б., Соловьев А. Д. Асимптотическая оценка надежности сложных систем с быстрым восстановлением // Тр. III Всесоюз. школы-совещ. по теории массового обслуживания. М.: Изд-во МГУ, 1975. Т. 1. С. 185–197.
3. Соловьев А. Д. Асимптотическое поведение момента первого наступления редкого события в регенерирующем процессе // Изв. АН СССР. Техн. кибернетика. 1971. № 6. С. 79–90.
4. Попов Г. А., Попова Е. А., Бурмистрова О. В. Анализ входных условий в модели информационной безопасности, построенной на основе аппарата редких событий // Науч. вестн. НГТУ. 2019. Т. 3. С. 112–131.
5. Попов Г. А. Асимптотическое поведение момента первого наступления редкого события в неоднородном регенерирующем процессе // Депон. ВИНИТИ. № 2193-В00, 2000. 46 с.
6. Попов Г. А., Попов А. Г., Лаптев П. В. Формализация процесса изменения вероятности нарушения сервисов информационной безопасности на основе аппарата редких событий // Наука, образование, инновации: пути развития: материалы VIII Всерос. науч.-практ. конф. (Петропавловск-Камчатский, 23–25 мая 2017 г.). Петропавловск-Камчатский: Изд-во Камчат. ГТУ, 2017. С. 56–61.
7. Ткаченко А. В. Многоканальные системы обслуживания с неидентичными приборами: дис. … канд. физ.-мат. наук. М.: Изд-во МГУ им. М. В. Ломоносова, 2013. 108 с.
8. Шилов Г. Е. Математический анализ. Специальный курс. М.: ГИФМЛ, 1961. 436 с.
9. Феллер В. Введение в теорию вероятностей и ее приложения. М.: Мир, 1984. Т. 2. 738 с.
