Республика Хакасия, Россия
Россия
Представлено исследование вопроса принятия решения по установлению цены продажи товара на микрорынках в торгово-посреднической сети. Описана упрощенная математическая модель взаимодей-ствия покупателя и продавца для одного вида продукции на микрорынке совершенной конкуренции. Анализируется поведение продавца, который находится в поиске заинтересованного покупателя. Производитель и/или продавец занимается перераспределением товара в сети и выбором цепочек доставки до конечного потребителя. При этом использован метод ценообразования по полной стоимости с учетом фактора воздействия спроса на реализуемый товар. Рассмотрена задача построения функции спроса и ее анализ на выпуклость с использованием ретроспективных данных и выявленных неценовых факторов. При определении цены продавец ориентируется на рынок покупателя, где присутствуют данные о предпочтениях и полезности получаемого товара в конкретных объемах для потребителя. Покупатель, учитывая свои потребительские предпочтения при ограничениях на свой бюджет, принимает решения о покупке. На микрорынке логистической сети сохраняется баланс между прогнозируемым спросом со стороны покупателя и доходом продавца от реализации товара. Функция дохода от реализации торговой сделки напрямую связана с функцией удельных затрат и коэффициентом наценки. Продавец принимает решение о выборе величины наценки на товар в зависимости от розничной, мелкооптовой и оптовой продажи по предложенному методу.
покупатель, продавец, логистическая сеть, торгово-посредническая система, товар, рыночный спрос, предложение, определение цены, принятие решений
Введение
Логистическая система является сложным объектом, который имеет на микроуровне свою организационную структуру, где в качестве элементов, взаимодействующих друг с другом, рассматриваются предприятия-производители, посредники и конечные потребители товара. Эти элементы системы рассматриваются с позиции взаимной связи как индивидуально, так и совместно. Однако они имеют единую цель, которой подчинено функционирование каждого из элементов. Ее достижение реализуется за счет анализа факторов логистической сети, связывающей элементы по материальным, финансовым и информационным потокам. Относительно распределения и продвижения товарного потока по сети понятие «логистическая сеть» в зарубежной литературе отождествляется с понятием «цепь поставок» либо с понятием «дистрибутивная сеть», что подразумевает процессы сбыта товара [1, 2].
В решении задачи распределения товарных потоков дистрибутивная сеть представляет собой запланированную совокупность каналов перемещения материальных запасов от одного или нескольких источников к центрам распределения и от них к конечным потребителям [3].
Одним из существенных факторов распределения товарных потоков является цена на микрорынках логистической сети. Под микрорынком будем понимать совокупность процессов, связанных с обменом между покупателями (потребителями) и продавцами (поставщиками) товаров [4].
Основными участниками на микрорынке являются агенты: продавцы и покупатели. Они опираются на имеющиеся в их распоряжении программные наработки, знания и опыт в осуществлении торговых сделок. Данный инструментарий предполагает наличие статистических (ретроспективных) данных и информации, необходимых для получения более точных прогнозов. Однако такого рода исходные данные порой недостаточны, неоднозначны, разрозненны и т. п. В таком случае присутствует неопределенность информации, что свидетельствует о наличии риска при выполнении операции купли/продажи. Присутствие неопределенности информации – отсутствие глубокого анализа, неэффективность управленческих решений, приводящих к необоснованным затратам в продвижении и хранении товарной продукции. Поэтому перед менеджерами стоит задача о снятии неопределенности, результатом которой является создание и применение инструментальных средств обработки информации, последующего анализа и выработки эффективных решений относительно определения цены.
Цель исследования состоит в моделировании определения цены при взаимодействии участников микрорынка логистической сети на основе метода ценообразования по полной стоимости.
Задача исследования заключается в рассмотрении закономерности динамики цен на микрорынке торгово-посреднической системы и построении модели взаимодействия экономических агентов логистической цепи с учетом спроса-предложения и их возможностей.
Новизна подхода состоит в том, что построенная модель позволит разработать алгоритм поддержки принятия решений с учетом динамики параметров при различающихся условиях микрорынка и возможностями последовательного приближения к равновесию между спросом и предложением.
Особенности формирования цены
Логистическую сеть можно представить в виде многоагентной системы, где взаимодействие экономических агентов происходит между собой, с потребительским рынком и рынком ресурсов. Потребительский рынок описывается выражением Θ = {Y(t), y0, μ}, где Y(t) – множество состояний рынка; y0 – начальное состояние рынка μ: Y(t) × Dsag → Y(t) – функция поведения рынка, Dsag(t) = {Dsag i(t) | i = 1, ..., n} – множество действий агентов цепи. На рис. 1 представлен элемент логистической сети, логистическая цепь описывается как Т = {Ag(t), Θ, Vs(t), St(t)}; где Ag (t) = {Agi | i = 1, ..., n} – множество агентов; Vs(t) – множество отношений между агентами; St(t) = {St1(t) × St2(t) × ... × Stn(t)} – множество состояний логистической цепи; Sti(t) – состояния i-агента. Каждый i-агент-посредник
Agi (t) = {Sti(t); Dsagi(t), Ogri(t), Ti}, где Dsagi(t) – действия i-агента, Ti: Stk × Dsi × Ogri → Stk+1 – функция переходов от состояния k к состоянию k + 1, Ogri(t) – множество ограничений i-агента.
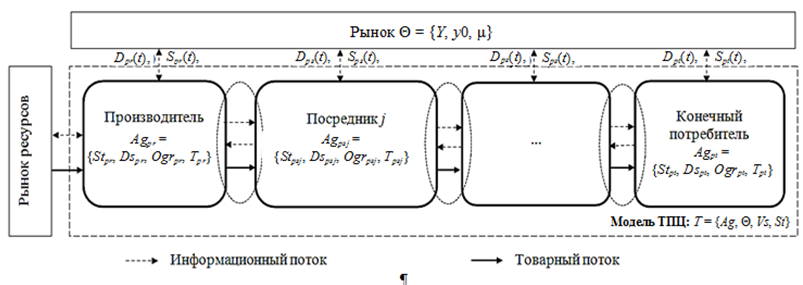
Рис. 1. Логистическая цепь «производитель-посредник-конечный потребитель»
Fig. 1. The logistics chain “Manufacturer-Intermediary-end Consumer”
С использованием базовой модели управления в организационных системах и механизма индивидуального стимулирования [5] разработана модель принятия решения при управлении логистической цепью с учетом взаимодействия экономических агентов:
Pag = {Аag, А0, Y, Fag, I}, Fag(·): Aag × Y(t) → A0,
где Aag – множество управляющих воздействий на деятельность агента; А0 – множество результатов выполнения работ после управляющего воздействия; Мag – множество мотивационных управляющих воздействий; I – информационное воздействие; Fag(·): А × Y(t) → А0 – целевая функция.
На микрорынке происходит обмен информацией о спросе IQd(p), предложении IQs(p), о цене Ip(t) и объемах IQ(t) продаж товара с учетом данных о текущем состоянии рынка товара. На основе такого взаимодействия принимается решение о покупке-продаже товара по договорной цене py(ty) и в соответствующем объеме Qy(ty) в определенный момент времени ty, удовлетворяющее обе стороны.
При принятии решения о покупке и продаже товара возникают моменты, которые необходимо учитывать, в том числе ограничения и возможности экономических агентов по продвижению товара,
а также цели участников и много других факторов.
Классическая теория А. Маршалла в определении цен опирается на наличие функций спроса и предложения. Но фактически цена устанавливается производителем или посредником сети [6]. Определение цены можно выполнить разными методами. Далее сделаем акцент на методе ценообразования по полной стоимости (себестоимость + прибыль) [7]. Она рассматривается как удельная себестоимость продукта, умноженная на коэффициент наценки (1 + m), где m – ставка наценки. Применение данного метода не предусматривает роли покупателя как участника, оказывающего влияние на уровень цены. Однако метод не исключает фактора воздействия спроса на реализуемый товар. Следовательно, рыночные правила и поведение рыночных игроков на микрорынках можно рассматривать как «рынок покупателя», когда поведение покупателя обусловлено наличием у него денежных средств, необходимых для приобретения товара. То есть рассматривается ситуация, при которой количество предложенного товара со стороны продавца будет соответствовать спросу на товар, приобретаемый покупателем.
В данном случае речь идет о неизменности цены на некотором интервале времени, хотя в реальности возможны изменения в зависимости от предлагаемых объемов реализации в розницу или оптом. Такой подход в определении цены для равновесного рынка согласуется с моделью Эрроу – Дебре [8].
Рассматривая вопрос о необходимости определения цен на микрорынках, обозначим роль термина «равновесие», который достаточно полно отражен в работе [9]. В логистической сети состояние экономического равновесия обусловлено тем, что продавец или производитель не принимает во внимание факторов эндогенного и/или экзогенного характера, под воздействием которых следовало бы изменить цену – как розничную, так и оптовую. Со стороны покупателя отсутствует возможность воздействовать на цены, поскольку ценовые факторы не зависят от него. В данном случае равновесие достигается исходя из возможностей всех участников микрорынка.
Если обратиться к фундаментальным идеям экономического равновесия (основоположником которых был Л. Вальрас), то далее речь будет касаться процессов совершенной конкуренции. Данная конкуренция отражает наличие идеализированного микрорынка. В нем рыночное поведение продавцов и покупателей заключается в приспособлении к имеющимся рыночным условиям. Однако в реальных условиях технологический процесс производства, продвижения и реализации продукции связан с наличием технологической конкуренции. В ней, с точки зрения когнитивизма, существенное внимание уделяется вопросам опережающего процесса обработки возрастающего количества данных и его эффективной обработки для создания новой информации. В эволюционной экономике все более важными для реального ведения бизнеса становятся процессы создания, отработки, хранения и передачи информации. Таким образом, реализуемые процессы выходят на уровень задач удовлетворения потребностей человека. Как отмечалось выше, в среде маркетинга существует такое понятие, как «рынок покупателя», когда рыночная стратегия и поведение производителя и продавца всегда строится от потребностей покупателя или потребителя. Согласно логистическому подходу на большинстве микрорынков сети принципиально изменяется задача производителя. Со сбыта и распределения ранее произведенной продукции задача производителя смещается в направлении реализации возможностей для гибкого производства и поиска «своего» потребителя. Очевидным фактором является оценка спроса, которую следует выявить для предлагаемого товара при назначенном уровне цен на него. Таким образом, величину спроса предстоит определить, ориентируясь при этом на возможности покупателя.
Для этой задачи можно построить функцию спроса QD = f(P), где P – цена товара. Чтобы построить функцию данного вида, можно воспользоваться ретроспективными данными, обращая внимание на заявки на товар от покупателя. Если значения показателей спроса подчиняются нормальному закону распределения случайной величины, то построение функции спроса не будет иметь каких-либо серьезных последствий. Однако наличие неценовых факторов осложняет построение функции спроса. Здесь следует обратить внимание на ряд утверждений [10]:
– эффект дохода: когда предоставляется возможность со стороны продавца предложить покупателю приобрести большее количество товара при снижении цены (розничные и оптовые цены), не уменьшая при этом дохода от продажи;
– эффект замещения: готовность покупателя при снижении цен на данный товар отдать предпочтение именно этому товару, т. к. другой более дорогостоящий;
– закон убывающей предельной полезности: предусматривает реакцию покупателя, когда товар будет приобретен только при снижении его цены;
– потребитель имеет право на приобретение всего объема произведенной и готовой к реализации продукции.
Определение цены продаж
Далее рассмотрим упрощенную математическую модель, полагая продажу одного вида продукции и наличие на микрорынке совершенной конкуренции, при условии, что покупатели не могут влиять на рыночную цену в одиночку и не формируют рыночный спрос на кратковременном интервале времени.
Задача индивидуального потребления заключается в следующем: какой объем товара может купить потребитель у продавца, чтобы максимально удовлетворить свои потребности. При этом суммарная стоимость купленного товара не должна превышать доход:
![]() , (1)
, (1)
где Pi – цена товара; Qi – объем реализуемого товара; DS – суммарный доход потребителя, выделенный для приобретения товара.
Отметим следующее: в выражении (1) DS связан с наличием бюджетных ограничений в поведении потребителя, т. е. приобретение товара ориентировано на величину предложенной цены на микрорынке и на запланированное количество приобретаемого товара. Каждая из пар (Pi, Qi) соотносится с функцией спроса на товар. При выполнении каждый раз выбора пары (Pi, Qi) величина
Di = PiQi вычитается из суммарного дохода: ![]() . Решая задачу о бюджетном ограничении, потребитель учитывает данное условие,
. Решая задачу о бюджетном ограничении, потребитель учитывает данное условие,
не исключая при этом пополнения дохода со стороны иных источников.
Принимая во внимание функцию спроса, отметим, что ее величина будет зависеть от предложенной цены на товар со стороны производителя
и дохода, которым располагает потребитель. Функция спроса является положительно однородной от одной переменной.
Прогнозируя спрос, следует сказать о том, как он будет реагировать на изменение цены, предлагаемой производителем при условии DS = const. Функция спроса, построенная исходя из наличия статистических и эмпирических данных, должна быть выпуклой. В частности, выпуклыми простыми функциями от одной переменной являются [11]:
– аффинная функция f(x) = ax + b на R;
– квадратичная функция f(x) = ax2 + bx + c на R при a > 0;
– экспоненциальная f(x) = ex на R и др.
Проверяя функцию спроса на выпуклость, необходимо следовать свойствам выпуклых функций, которые представлены в классической литературе по математическому анализу. Критерием выпуклости является дважды дифференцируемость функции.
В качестве примера о выпуклости рассмотрим функцию спроса вида f(x) = d / x, где x = P – цена, y = Q – объем покупки. Точка разрыва функции x = 0, т. к. f(x) = –f(x) , то функция является нечетной. Первая производная c f ' (x) = –d / x2. Точек экстремума нет, и на интервале (0; +∞) функция f ' (x) ˂ 0, т. е. является убывающей. При исследовании на выпуклость и вогнутость находим вторую производную, которая будет иметь вид f" (x) = 2d / x3 и f" (x) ≠ 0. На интервале (0; +∞) функция f" (x) > 0, т. е. является вогнутой. Таким образом, подтверждено условие выпуклости (вогнутости) функции, т. к. исходная функция дважды дифференцируема.
Далее затронем вопрос потребительского выбора. На микрорынке торгово-посреднической сети товар и его потребители являются основными элементами торговых сделок. В перспективе потребители прогнозируют и распределяют свой суммарный доход на покупку товаров у производителя/поставщика. В свою очередь, продавец должен спрогнозировать величину дохода, используя который покупатель приобретет необходимое количество товара в заданных ценах для удовлетворения своих потребностей.
Ранее было отмечено, что в торгово-посреднической системе предлагается рассмотрение реализации товара одного вида. Объем покупок Q измеряется вещественным неотрицательным числом. Товар обладает свойством произвольной делимости, т. е. может быть закуплено любое его количество при условии Qmin ≤ Q ≤ Qmax в границах, установленных продавцом.
Все возможные наборы товара (в обозначенных границах) – вектор y R1 с неотрицательными компонентами.
Чем руководствуется покупатель/потребитель товара? Удовлетворение собственных потребностей: для конечного потребителя – польза от последующего использования, для посредника – получение дополнительного дохода от перераспределения товара в сети и удовлетворение спроса конечного потребителя. Приобретая товар, потребитель опирается на ряд предпочтений. Например, для выбора количества товара yi и yj из набора, запись yi ≥ yj означает, что потребитель либо предпочитает приобрести количество товара yi, либо не делает между ними различий. В данном случае вводится понятие «отношение безразличия (эквивалентности)»: наборы yi и yj безразличны (эквивалентны) для потребителя: yi ~ yj. Можно также рассматривать отношение строгого предпочтения, когда потребитель предпочитает набор yi набору yj: yi > yj.
Практическое рассмотрение предпочтений может быть реализовано, например, на основе ретроспективных данных о реализации товара, находящихся в ведении продавца. Анализ этих данных, их классификация и кластеризация позволят выявить предпочтения как по количеству товара, так и по качественным признакам потребителей (данный анализ в настоящей работе не рассматривается). Отношения предпочтения преимущественно являются качественной категорией и малоприменимы для количественных решений. Здесь уместно воспользоваться количественной характеристикой – функцией полезности, связанной с отношением предпочтения: u(xi) ≥ u(xj) при xi ≥ xj.
Рассмотрим условия, при которых функция полезности u(x) применима в расчетах.
Строго возрастающая функция j(·) одной переменной может рассматриваться как функция полезности j(u(x)). Такая функция, в частности, может иметь вид j(u(x)) = a · u(x) + b, где
a > 0j2(u(x)) = eu(x).
Функция u(x) дифференцируема, а ее частные производные положительны ![]() , представляют собой предельную полезность i-го товара. Ее положительные величины означают возрастание потребности i-го товара и ведут к увеличению полезности набора.
, представляют собой предельную полезность i-го товара. Ее положительные величины означают возрастание потребности i-го товара и ведут к увеличению полезности набора.
Если u(x) дважды дифференцируема и является отрицательной, это свидетельствует о ее вогнутости. Согласно критерию Сильвестра отрицательность означает: предельная полезность любого товара уменьшается по мере его потребления (закон Госсена).
Следует отметить, что при данных принятых условиях такие понятия, как предпочтения и функция полезности, определены только на одном виде товара.
Спрос на предлагаемый продавцом товар связан с потребительским выбором. Здесь востребован анализ принятия решений потребителем о соблюдении условий, ограниченных наличием необходимых денежных средств и ценами предлагаемых товаров. В условиях совершенной конкуренции потребительский выбор связан с формированием дохода и бюджетных ограничений.
Задача индивидуального потребительского выбора ориентирована на определение количества товара, которое следует купить потребителю на микрорынке, чтобы удовлетворить свой спрос. При этом суммарная стоимость купленного товара не должна превышать его доход (1). Представим (1) в следующем виде:
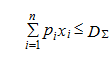 ,
,
где pi – цена товара i-го предпочтительного выбора; xi – объем товара, приобретенного в выборе i; DΣ – суммарный доход, которым располагает потребитель.
Все множество n покупок товара, доступных потребителю для закупки, можно выразить как
![]() ,
,
где p – цена товара; x – объем товара; Ω – множество возможных покупок.
Обращаясь к вопросу о предпочтениях и их отношениях, наша задача сводится к выбору из имеющегося множества B(p, DΣ) наиболее предпочтительного варианта x*, т. е. к отношению ![]()
при условии x* ≥ x.
Если будет определена величина р, то количественная величина x будет найдена при известной функции полезности u(x).
Обратимся к задаче производственного характера, считая, что производитель занимается выпуском и реализацией одного вида товара. Все виды затрат являются неотрицательными величинами и не меняются на интервале времени до смены технологического процесса. Каждой точке пространства затрат можно сопоставить функцию выпуска продукции f(x). Такого рода связь между затратами и выпуском продукции получила название производственной функции. Она характеризуется постоянным доходом от расширения мощности производства, указывая на следующее: выпуск возрастает
в той же пропорции, что и затраты. Существуют примерные производственные функции, которые можно построить для конкретной задачи.
Рассмотрим микрорынок логистической системы как равновесный, когда спрос находит удовлетворение при наличии предложения товара. При установленной цене спрос на товар равен его предложению, что свидетельствует о наличии равновесной цены. Рассматривая понятие спроса индивидуального потребителя и предложение отдельного продавца, например производителя, результат решения связывают с экстремальными задачами. Их решение достигается двумя возможными путями:
1. Построение функции полезности всех потребителей товара и определение рыночного спроса через оптимизацию данной функции. Однако здесь возможны существенные затруднения: необходим учет отношения предпочтений, отразить которые принципиально сложно ввиду наличия неопределенности необходимой информации.
2. Определение рыночного спроса, исходя из решения индивидуальной задачи построения функции полезности одного потребителя.
На основе информации о рыночном спросе возможно построение индивидуального спроса потребителя. Рыночное предпочтение характеризуется функцией предложения производителя. Если обратиться к условиям существования «совершенной конкуренции» (при наличии на рынке большого числа продавцов и покупателей), имеющим идеализированный характер, такая конкуренция носит абстрактный характер. Принимая ее во внимание, выделим ряд признаков:
– на микрорынке имеются фирмы, реализующие один и тот же товар, доля выпуска и реализации товара каждой фирмы незначительна по сравнению с реализацией товара всех фирм;
– наличие большого числа независимых покупателей товара, доля дохода отдельного покупателя незначительна по сравнению с суммарным объемом реализуемого товара;
– совершенное знание рынка (прежде всего цен и денежных средств на приобретение товара) покупателями и продавцами.
Упомянутые признаки дают нам основание предположить, что на микрорынке взаимодействуют продавец и покупатель, каждый из которых представляет собой некий эквивалент соответствующих свойств и признаков участника рынка.
В ответе на вопрос об определении цены решение задачи не предполагает одновременного определения цены и количества товара, т. е. спроса и предложения. Как показывает практика рыночных отношений, цена и количество товара обычно определяются независимо друг от друга [7].
Установление цены будем рассматривать в следующем порядке. Продавец устанавливает свою цену на товар, исходя из затрат, которые он несет в зависимости от осуществления материально-производственной деятельности. Производимый товар, имеющий абстрактное содержание и общие характеристики, распределяется при продвижении в торгово-посреднической сети и реализуется на микрорынках. Цена продажи устанавливается исходя из стоимости единицы продукции C и ставки наценки m к ней как p = (1 + m) · C, где (1 + m) – коэффициент наценки. Важным здесь является
не столько калькулирование С, сколько определение наценки m. Калькулирование затрат предполагает наличие детерминированных данных, тогда как наценка связана с учетом факторов, обуславливающих неопределенность.
Такого рода учет затрат ориентирован на условие неизменности стоимости единицы товара. Изменения при пересчете стоимости возникнут только при изменении технологии производства.
Как было отмечено выше, установление цены производителем/продавцом связано с тем, что потребители/покупатели вправе принимать решения о количестве товара, приобретаемого по установленной цене. Таким образом, на микрорынке логистической системы решение о покупке/продаже обусловлено двумя сторонами:
– производители (или продавцы) определяют цену продажи;
– потребители (или покупатели) определяют количество приобретаемого товара.
В такой системе присутствуют торговые сделки, но отсутствует торг. Производители ориентируются на спрос, прогнозируя цены, потребители – на предложенные цены.
Доход от реализации торговой сделки D рассчитывается по формуле
![]() , (2)
, (2)
где (1 + m) – коэффициент наценки; С(·) – функция удельных затрат; Q – объем продаж за рассматриваемый период времени. Из (2) следует: если наценка постоянна, при росте объема продаж доход увеличивается.
В выражении (2) функция удельных затрат С(·) при выполнении расчетов имеет нелинейный вид. Например, согласно [11], при расчете затрат на управление запасами используют две категории затрат: удельные и за анализируемый период. Удельные затраты включают закупочную стоимость, цену товара (розничную, мелкооптовую, оптовую, договорную) у поставщика, затраты на доставку и хранение товара с учетом их деления на количество единиц доставки и хранения запасов. Практика содержания запасов показывает, что годовые затраты составляют от 20 до 30 % стоимости запаса [11]. Если затраты на хранение единицы запаса в единицу времени (год) известны, можно определить величину удельных затрат на хранение запасов. Общие удельные затраты вычисляются исходя из ряда составляющих:
![]() , (3)
, (3)
где P – закупочная стоимость единицы товара; Т – продолжительность анализируемого периода; Qпр – спрос на единицу товара за анализируемый период; Y – удельные затраты на хранение запаса;
К – удельные затраты на создание запаса. Все представленные составляющие относятся к неуправляемым параметрам.
Подставив (3) в (2), можно определить доход от реализации продукции, где m является управляемым параметром и подлежит определению. Вычисленные C и D в данных выражениях носят детерминированный характер, тогда как прогнозируемый спрос – вероятностный.
Стоимость приобретаемого товара составляет
Dпр = p · Qпр,
где p – цена приобретения товара; Qпр – функция спроса. Величина Qпр описывается функцией вида Qпр = f(p, Dр), где Dр – денежные средства, которыми располагает потребитель товара при его покупке.
В процессе купли/продажи при условии рыночного равновесия сохраняется баланс:
D = Dпр => (1 + m) × C × Q = p × f(p, Dр). (4)
Функция f(p, Dр) формируется на основе прогнозных оценок, полученных исходя из реализации отношения предпочтений и полезности.
Из баланса (4) можно вычислить надбавку к стоимости единицы продукции:
(1 + m) = p × f(p, Dр) / (C × Q).
Задавая значение Q на линии функции f(p, Dр), получаем значение наценки. При этом очевидно: величина наценки распределится на всей функции спроса при условии соблюдения ограничений объема производимой продукции или запасов на складах.
Величина наценки на практике относится к граничным значениям цены: p = (1 + m) × C. Рассматривается, как правило, розничная, мелкооптовая и оптовая цена. Поэтому все значения (1 + m3) × С3 предстоит разделить на диапазоны. При этом желательно, чтобы доход от реализации (2) в ценах по каждому из диапазонов был постоянным (рис. 2).
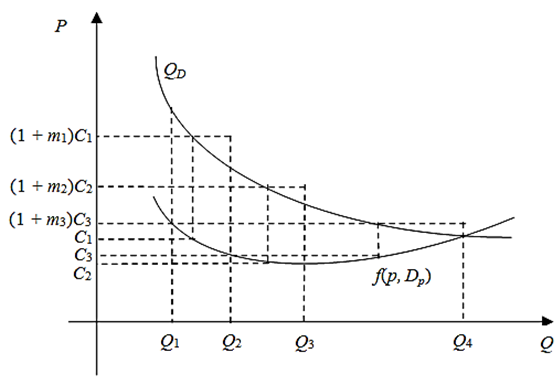
Рис. 2. Отображение диапазонов цены при реализации товара
Fig. 2. Displaying price ranges when selling goods
Установление цены при продаже товара предполагает, что производители ориентируются на затраты и определяют наценку, учитывая неопределенности, связанные с рыночными условиями. Потребители принимают решения о количестве приобретаемого товара по установленной цене. Происходит динамическое взаимодействие между сторонами. Система управления предложением и установления коэффициента наценки позволит на основе моделирования ценовых диапазонов установить соответствующие объемы продаж на основе ретроспективных данных спроса на товар.
Заключение
Одним из подходов к определению цены на микрорынке торгово-посреднической системы можно считать сохранение баланса между прогнозируемым спросом со стороны покупателя и доходом от реализации товара продавцом. Определение значения цены связано с вычислением надбавки себестоимости единицы продукции, что отличается от поиска цены при условии баланса между спросом и предложением (где в основе лежит «крест Маршалла»).
Ориентация продавца на рынок покупателя – основной прием формирования цены. Реакция со стороны продавца на сложившийся спрос представляет собой выработку прогнозных решений, исходным аргументом которых являются предпочтения и полезность получаемого товара в конкретных объемах для потребителя. Результаты исследования могут быть использованы при построении интеллектуальных систем поддержки принятия решения.
1. Supply Chain Today. URL: http://www.supplychaintoday.com (дата обращения: 20.01.2024).
2. Твердохлебова М. Д. Дистрибуция // Большая российская энциклопедия: научно-образовательный портал. URL: https://bigenc.ru/c/distrib-iutsiia-79a7bd/?v=7982138 (дата обращения: 25.01.2024).
3. Макконнелл К. Р., Брю С. Л. Экономикс: принципы, проблемы и политика. М.: Республика, 1992. Т. 1. 399 с.
4. Новиков Д. А. Теория управления организационными системами. М.: ЛЕНАНД, 2021. 636 с.
5. Shiozawa Y. The primacy of stationarity: A case against general equilibrium theory // Osaka City University Economic Review. 1989. V. 24 (1). P. 85–110. URL: https://www.researchgate.net/publication/233943723_The_Primacy_of_Stationarity_A_Case_against_General_Equilib-rium_Theory (дата обращения: 10.03.2024).
6. Shiozawa Y. A new framework for analyzing technological change // Journal of Evolutionary Economics. 2020. V. 30. P. 989–1034.
7. Arrow K., Debreu G. Existence of equilibrium for a competitive economy // Econometrica. 1954. V. 22. N. 3. P. 265–290. URL: http://web.stanford.edu/class/msande311/arrow-debreu.pdf (дата обращения: 28.01.2024).
8. Полтерович В. И. Экономическое равновесие и хозяйственный механизм. М.: Наука, 1990. 256 с.
9. Вэриан Х. Р. Микроэкономика. Промежуточный уровень. Современный подход. М.: ЮНИТИ, 1997. 767 с.
10. Дудов С. И., Выгодчикова И. Ю., Купцов С. Н. Математические методы в экономике. URL: https://obuchalka.org/2015051184621/matematicheskie-me-todi-v-ekonomike-dudov-s-i-vigodchikova-i-u-kupcov-s-n-2014.html (дата обращения: 12.03.2024).
11. Линдерс М. Р., Харольд Е. Ф. Управление снабжением и запасами. Логистика / пер. с англ. СПб.: Полигон, 1999. 768 с.















