Россия
Россия
Исследовано влияние одноосной распределенной нагрузки в плоскости тонкой прямоугольной пластинки на величину первой собственной частоты ее колебаний. Рассматривалась пластинка, две противоположные грани которой защемлены, а две другие свободны (CFCF-пластинка: C-clamped, защемленная грань, F-free, свободная грань). Нагрузка приложена к защемленным граням. Основное дифференциальное уравнение для координатной составляющей функции прогибов и все граничные условия задачи выполнены точно с помощью двух гиперболо-тригонометрических рядов по двум координатам и дополнительной функции, зависящей от одной переменной x. Проблема свелась к бесконечной системе линейных алгебраических уравнений относительно одной последовательности неопределенных коэффициентов, содержащей в качестве параметров величину нагрузки и частоту колебаний. Для ряда значений нагрузки находились собственные частоты колебаний методом перебора значений частоты в сочетании с методом последовательных приближений при решении редуцированной системы линейных алгебраических уравнений. Для обеспечения приемлемой точности вычислений менялось число членов в рядах (размер редуцированной системы), число итераций и число значащих цифр в мантиссе при вычислении нетривиальных коэффициентов системы. В качестве примера рассматривалась квадратная пластинка. По результатам расчетов построен график зависимости первой собственной частоты колебаний от величины усилий растяжения-сжатия, который представляет собой кривую, близкую к параболе. При эйлеровой сжимающей нагрузке колебания прекращаются. Формы собственных колебаний изменялись незначительно и были подобны форме изогнутой поверхности пластинки под действием равномерной поперечной нагрузки. Целью данного исследования является создание эффективного алгоритма вычисления собственных частот колебаний CFCF-пластинки при изменении одноосной нагрузки растяжения-сжатия ее защемленных граней.
CFCF-пластинка, собственные колебания, растяжение-сжатие, сжимающая нагрузка
Введение
Тонкие CFCF-пластинки (наряду с CFFF, CCCC-пластинками) используются в микроэлектронике, smart-конструкциях в качестве чувствительных элементов различных датчиков. Эти пластинки могут находиться под действием плоских внешних или внутренних электрических или магнитных полей, совершая при этом свободные колебания. При изменении усилий растяжения-сжатия собственная частота колебаний будет меняться и через сенсоры, актуаторы вызывать тот или иной отклик управляющей системы. Проблема определения собственных частот колебаний при сжимающей нагрузке в ее плоскости рассматривалась в работах [1–5], однако лишь некоторые исследования имеют численные результаты для CFCF-пластинки при одноосном растяжении-сжатии.
В работе [1] решение получено при использовании тригонометрических и гиперболических функций и принципа виртуальной работы. Приведены численные результаты собственных частот ортотропной CFCF-пластинки при сжатии по защемленным граням. В работе [2] использовался асимптотический метод и аналогичные базовые функции для вычисления собственных частот, однако численные результаты не представлены.
Статья [3] посвящена собственным колебаниям ортотропного графенового листа в упругой среде при двухосной нагрузке в его плоскости. Задача рассматривалась в рамках нелокальной теории упругости. Разрешающие уравнения решались методом дифференциальных квадратур для различных граничных условий.
В работе [4] получены замкнутые решения для прямоугольных нанопластин при двухосном сжатии сторон (с одинаковой интенсивностью) в рамках нелокальной теории Эрингена. Исследована зависимость собственных частот и критических сил от нелокального параметра нанопластины. Численные результаты получены при различных условиях опирания пластинки, в том числе и для CFCF-пластинки.
Работа [5] посвящена колебаниям защемленной пластины при двухосном сжатии ее сторон. Показано, что частоты колебаний убывают по параболическому закону с ростом сжимающей нагрузки до ее эйлерова значения. Использовался тот же метод исследования, что и в настоящей работе, который также успешно применялся авторами в работах [6, 7].
Отметим и обзорную работу [8], посвященную колебаниям и устойчивости пластинок из функционально градуированного материала, которые находят широкое применение в полупроводниковой технике и биомеханике.
Математическая постановка задачи
Пусть прямоугольная CFCF-пластинка постоянной толщины h с размерами a и b в плане совершает свободные колебания и при этом сжимается (растягивается) по защемленным граням равномерно распределенными усилиями интенсивности TX (рис. 1).
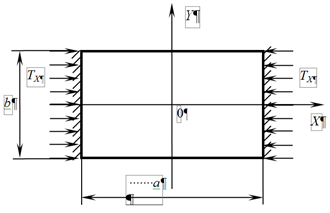
Рис. 1. Схема нагружения CFCF-пластинки
Fig. 1. CFCF plate loading scheme
Требуется определить зависимость собственных частот колебаний от величины TX усилий растяжения-сжатия.
Основное уравнение задачи [9] имеет вид
(1)
где D – упругая постоянная (жесткость) пластинки, кГ·м; ΔΔ – двумерный бигармонический оператор; W(X, Y, t) – нормальная деформация срединной поверхности (прогиб), м, t – время, с; ρ – плотность вещества пластинки, кг/м3.
В безразмерных координатах x = X / b, y = Y / b уравнение (1) перепишется следующим образом:
(2)
где Tx = TXb2 / D – безразмерная интенсивность сжатия (при растяжении меняется знак); η2 = ρhb4 / D; размеры пластинки: x ∈ [–γ / 2; γ / 2], y ∈ [–1 / 2; 1 / 2], γ = a / b – отношение сторон.
Граничные условия [9]:
(3)
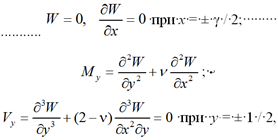
где My, Vy – безразмерные изгибающие моменты и перерезывающие силы соответственно; ν – коэффициент Пуассона.
Заметим, что задача математической физики (2)–(4) имеет тривиальное решение, но здесь требуется найти отличную от нуля функцию W (x, y, t), удовлетворяющую условиям (2)–(4), а также начальным условиям для поля перемещений и скоростей всех точек пластины, которые должны быть заданы для конкретной задачи колебаний пластинки.
Метод решения
В искомой функции прогибов разделим переменные [9]:
W (x, y, t) = w* (t) w (x, y), (5)
где w(x, y) – координатная функция с граничными условиями (3), (4), а функция времени представлена выражением
w*(t) = Asin(pt + φ), (6)
в котором A, φ – произвольные постоянные, которые должны определяться из заданных начальных условий; p – искомая частота собственных колебаний пластинки. С учетом (5), (6) из уравнения (2) получим для координатной функции прогибов уравнение [9]
(7)
где Ω = pη – безразмерная частота собственных колебаний пластинки.
Функцию w(x, y) будем разыскивать в следующем виде:
w(x, y) = w1(x, y) + w2(x, y), (8)
где
(9)
(10)
где k = 1, 2, 3…; s* = (s + 1) / 2; коэффициенты Ak, Cs, αk, ξs подлежат определению; λk = 2πk; μs = πs / γ.
Заметим, что первая форма собственных колебаний должна быть симметричной относительно обеих осей координат, поэтому здесь используются четные функции.
Коэффициенты αk, ξs найдем при подстановке (9) и (10) в уравнение (7):
отсюда находим пары корней
где вторые значения искомых корней αk и ξs обозначены через βk и ηs соответственно.
В силу четности функций соответствующие отрицательные корни не рассматривались.
Функции (9), (10) перепишутся теперь в следующем виде:
(11)
(12)
Здесь добавились слагаемые с коэффициентами Bk и Ds.
Заметим, что функция w2(x, y) автоматически дает нулевые прогибы граней x = ±γ / 2, а функция w1(x, y) – нулевые перерезывающие силы на гранях y = ±1 / 2. Чтобы функция w1(x, y) также не давала прогибов защемленных граней, а функция w2(x, y) обеспечивала нулевые перерезывающие силы на свободных гранях, коэффициенты рядов (11) и (12) должны быть связаны соотношениями
где
.
Тогда искомая функция прогибов (8) примет вид
(13)
Удовлетворяя теперь второму условию (3) и первому условию (4), получим систему
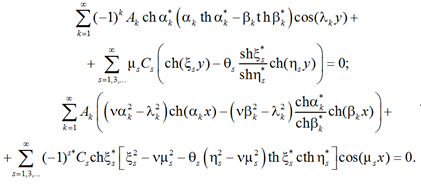(14)
Преобразуем систему (14). Для этого в первом уравнении разложим гиперболические функции в ряды Фурье по cos(λky), а во втором уравнении – по cos(μsx). Воспользуемся разложениями [10]:
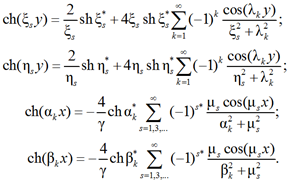(15)
При подстановке первых двух разложений (15) в первое уравнение (14) в нем появится свободный член
. (16)
Для устранения полученной невязки добавим к функции (13) дополнительный прогиб:
w0(x) = Rch(ωx), (17)
где R, ω – неопределенные коэффициенты.
Подчиним функцию (17) основному уравнению задачи (7). Тогда
откуда
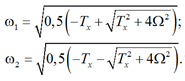
Функция (17) запишется теперь в виде суммы двух слагаемых:
(18)
Потребуем от функции (18) выполнения граничных условий при x = ±γ / 2, тогда
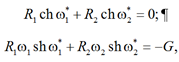
где ω1* = ω1γ / 2, ω2* = ω2γ / 2.
Из этой системы получаем
Первое уравнение (14) без свободных членов примет вид
а после перестановки знаков суммирования по индексам k и s и освобождения затем от знака суммирования по индексу k получим
(19)
Функция (18) нарушает первое условие (4) на гранях y = ±1 / 2:
Разложим эту невязку в ряд Фурье по cos(μsx). По аналогии с последней формулой (15) имеем
где вместо ω надо подставить ω1 или ω2; тогда
(20)
где
Подставим теперь две последние формулы (15) во второе уравнение (14) и добавим невязку (20):
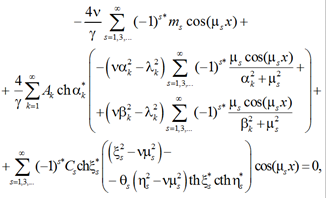
что затем приводит это уравнение к виду
(21)
Из уравнения (19) следует, что
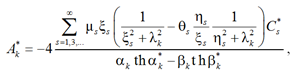, (22)
где введены обозначения: 
.
Из уравнения (21) получаем
(23)
и тогда выражение (16) примет вид
. (24)
Выражение (23), с учетом (22) и (24), представляет собой бесконечную однородную систему линейных алгебраических уравнений для одной последовательности коэффициентов В качестве основных параметров она содержит искомую частоту собственных колебаний Ω и интенсивность усилий Tx в плоскости пластины. Эту частоту при заданном значении Tx можно найти из условия равенства нулю определителя системы (23), что является отдельной трудоемкой задачей.
В данном случае использовался не традиционный метод отыскания корней определителя системы (23), а итерационный процесс [5] вычисления нетривиальных коэффициентов в сочетании с методом перебора частотного параметра Ω. Стандартная форма бесконечной системы (23), когда искомые коэффициенты присутствуют отдельно в ее левой части и под знаками сумм в правой части, позволяет легко организовать вычислительный процесс последовательных приближений. Начальные значения коэффициентов можно назначить произвольно, например, для сжимающей нагрузки = 1 / μ2s.
Коэффициенты редуцированной системы (23), число уравнений которой менялось, выводились на печать на каждой итерации. Если соответствующие нетривиальные коэффициенты, начиная с некоторой итерации, не отличались друг от друга, то данная частота принималась за собственную (при заданной нагрузке).
Приведем окончательное выражение для функции прогибов пластинки:
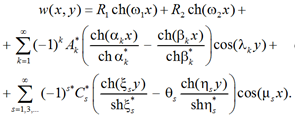(25)
Численные результаты. Обсуждение
Вычисления производились в системе аналитических вычислений Maple по программе, которая позволяла менять коэффициент Пуассона, отношение сторон пластины, безразмерную величину сжимающей (растягивающей) нагрузки, безразмерную частоту колебаний, число членов в рядах (размер редуцированной системы), число итераций и количество значащих цифр в мантиссе чисел при вычислениях. Окончательно число членов в рядах принималось равным 90, число итераций – 20, количество значащих цифр при вычислениях – 40.
В таблице приведены полученные собственные относительные частоты колебаний квадратной пластины для ряда значений сжимающих и растягивающих усилий. Коэффициент Пуассона был принят равным 0,3.
|
Tx |
–10* |
–5 |
0 |
1 |
3 |
4 |
10 |
15 |
|
Ω |
24,775 |
23,51045 |
22,1653 |
21,8854 |
21,3133 |
21,0208 |
19,1634 |
17,4509 |
|
Tx |
22 |
27 |
33 |
35 |
37 |
38 |
38,6752 |
– |
|
Ω |
14,6938 |
12,3261 |
8,6216 |
6,9460 |
4,6950 |
2,9825 |
0 |
– |
* Отрицательные Tx являются растягивающими усилиями.
Следует отметить, что для сжимающих усилий функция прогибов на соответствующих собственных частотах была вещественной, но при растягивающих усилиях она получалась комплексной ввиду сложности граничных условий задачи (наличие свободных краев), поэтому для получения вещественного решения последовательность C*s0 = 1 / μ2s умножалась еще и на комплексно-сопряженное выражение при Cs в формуле (16), с использованием оператора Maple conjugate(d[s]), где
.
Вывод об этом был сделан на основании того, что начальные значения коэффициента G (16) оказались комплексными для растягивающих усилий. Заметим, что искомые коэффициенты функции (25) находятся с точностью до постоянного множителя (одинакового для всех коэффициентов) в силу линейности и однородности основного уравнения (1) задачи.
По данным таблицы в системе Maple был построен график зависимости Ω = f (Tx), который представляет собой кривую, близкую к параболе (рис. 2), вершиной которой является значение эйлеровой сжимающей нагрузки Txэ = 38,6752.
Рис. 2. Зависимость частоты собственных колебаний квадратной CFCF-пластины
от величины сжимающей (растягивающей) нагрузки Тх, приложенной к защемленным граням
Fig. 2. Dependence of the natural oscillation frequency of a square CFCF plate
on the magnitude of the compressive (tensile) load Tx applied to the pinched faces
Это значение близко к значению Txэ = 39,321 (расхождение 1,6 %), полученному в работе [11], в которой для определения критических нагрузок использовался метод конечных элементов с усовершенствованным 9-узловым элементом. Задача решалась по уточненной теории Рейсснера – Миндлина, учитывающей деформацию поперечного сдвига (пластины средней толщины).
С ростом сжимающей нагрузки частота собственных колебаний уменьшается и при критическом значении обращается в нуль, т. е. колебания отсутствуют. Наоборот, с уменьшением сжатия частота увеличивается. При отсутствии нагрузки получили частоту свободных колебаний Ω = 22,1653. Последнее значение хорошо совпадает со значением Ω = 22,1166 (расхождение 0,2 %), полученным в работе [10].
График позволяет приближенно найти собственную частоту колебаний пластины при других значениях сжимающей нагрузки, а затем с помощью вычислительной программы быстро уточнить ее.
При отыскании собственных частот в системе Maple строились и соответствующие 3D-формы равновесия. На рис. 3 представлена форма свободных колебаний при отсутствии нагрузки, а на рис. 4 – форма потери устойчивости при эйлеровой нагрузке, где по вертикальной оси откладывались прогибы w.
Рис. 3. Форма свободных колебаний при Tx = 0, Ω = 22,1653
Fig. 3. The shape of free oscillations at Tx = 0, Ω = 22.1653
Рис. 4. Форма потери устойчивости
при Tx = 38,6752, Ω = 0
Fig. 4. The form of loss of stability
at Tx = 38.6752, Ω = 0
Отметим, что все полученные формы подобны изогнутой поверхности пластинки при изгибе равномерным давлением. С ростом сжимающей нагрузки на защемленные грани немного уменьшались амплитуды.
Заключение
Полученные результаты могут быть использованы при проектировании тонких и сверхтонких пластинок (мембран и нанопластин) в качестве чувствительных элементов различных датчиков в смарт-конструкциях. При изменении усилий растяжения-сжатия плоскости пластинки меняются собственные частоты ее колебаний, что вызывает соответствующий отклик управляющей системы.
Предложенный метод позволяет находить собственные частоты и для пластинок с другими граничными условиями.
1. Kshirsagar S., Bhaskar K. Accurate and elegant free vibration and buckling studies of orthotropic rectangular plates using untruncated infinite series // Journal of Sound and Vibration. 2008. V. 314. P. 837–850.
2. Баничук Н. В., Барсук А. А., Иванова С. Ю. Асимптотический анализ свободных колебаний и устойчивости растянутых и сжатых упругих полос и прямоугольных пластинок // Проблемы прочности и пластичности. 2010. Вып. 72. С. 93–99.
3. Mohammadi M., Goodarzi M., Ghayour M., Alivand S. Small scale effect on the vibration of orthotropic plates embedded in an elastic medium and under biaxial in-plane pre-load via nonlocal elasticity theory // Journal Solid Mechanics. 2012. V. 4. N. 2. P. 128–143.
4. Wang Z., Xing Y., Sun Q., Yang Y. Highly accurate closed-form solutions for free vibration and eigenbuckling of rectangular nanoplates // Composite Structures. 2018. V. 210. P. 28.
5. Сухотерин М. В., Глухих В. Н., Войтко И. В., Пастушок Е. М. Колебания защемленной прямоугольной пластины при растяжении-сжатии ее плоскости // Строительная механика и расчет сооружений. 2023. № 3. С. 7–14.
6. Сухотерин М. В., Потехина Е. В., Анненков Л. В. Определение спектра критических нагрузок и форм равновесия сжатых панелей обшивки корпуса судна // Вестн. гос. ун-та мор. и реч. флота им. адм. С. О. Макарова. 2014. № 2 (24). С. 44–51.
7. Барышников С. О., Сухотерин М. В., Кныш Т. П. Устойчивость внешних консольных элементов глубоководных аппаратов // Вестн. гос. ун-та мор. и реч. флота им. адм. С. О. Макарова. 2020. № 2. С. 347–358.
8. Swaminathan K., Naveenkumar D. T., Zenkour A. M., Carrera E. Stress, vibration and buckling analyses of FGM plates. A state-of-the-art revive // Composite Structures. 2015. V. 120. P. 10–31.
9. Лехницкий С. Г. Анизотропные пластинки. М.; Л.: Изд-во ОГИЗ–ГИТТТЛ, 1947. 355 с.
10. Сухотерин М. В., Лалин В. В., Кондратьева Л. Н., Барышников С. О., Войтко И. В. Свободные колебания прямоугольной пластины с защемленными противоположными краями (CFCF-пластина) // Науч.-техн. ведом. Санкт-Петерб. гос. политехн. ун-та. Физ.-мат. науки. 2023. Т. 16. № 1. С. 51–64.
11. Lee S. J. Buckling analysis of rectangular plates us-ing an enhanced 9-node element // Architectural Research. 2016. V. 18. N. 3. P. 113–120.
