Россия
Россия
Рассматривается возможность автоматизации качественного оценивания решений задач по программированию при обучении учащихся средней школы. Рассмотрены существующие на данный момент способы оценивания решения задач по программированию, выделены их преимущества и недостатки. На основе рассмотренных способов обоснована возможность использования представления исходного кода решения задачи в виде семантической сети для его дальнейшего качественного оценивания машинными методами. Вводится понятие функции подобия двух семантических сетей, построенных на программном коде. Данная функция определяется как отношение суммы размеров подграфов, составленных из общих элементов семантических сетей, к сумме размеров исследуемых сетей. Приводятся свойства получаемой функции, вытекающие из ее определения, а также приводится алгоритм вычисления функции подобия, созданного на основе алгоритма ISD. Рассматриваются различные модификации указанного алгоритма, обосновывается влияние каждого из них на итоговый результат. Для проверки работоспособности алгоритма был поставлен эксперимент по сравнению различных решений задачи по поиску максимального элемента, а также сравнению решений для различных задач базового курса программирования между собой. Результаты эксперимента приведены в сводной таблице и позволяют обосновать выбранную модификацию алгоритма расчета функции подобия. Результаты также демонстрируют перспективность использования данного метода для определения компетентности обучаемых в изучаемом языке программирования. В качестве побочного результата алгоритм качественного оценивания программного кода на основе его семантической сети позволяет осуществлять автоматическую проверку на плагиат программного решения задачи.
программирование, решение задач, программный код, исходный код, функция подобия, модификация алгоритма
Введение
В контексте современной идеологии подготовки специалистов формируются новые задачи развития образовательного процесса, в котором основное место уделяется личностно-ориентированному образованию. Возникает потребность в индивидуализации траектории обучения путем предоставления каждому учащемуся возможности создания собственной образовательной траектории освоения учебной дисциплины. Чтобы внедрить такой подход на ранних этапах обучения, в частности в средней и старшей школе, необходимо в онлайн-формате определять уровень компетентности обучаемого и качество усвоения им учебного материала [1].
Если рассматривать процесс обучения прикладному программированию, то основным артефактом, по которому можно оценивать способности обучаемых, является написанный ими исходный код, который, как правило, и является решением поставленных учебных задач. При обучении программированию подходы к оцениванию решений можно условно поделить на тестирование и экспертный анализ.
Тестирование программного решения производится с помощью запуска исходного кода на заранее заданном наборе входных данных. По завершении работы программы ее вывод сравнивается с эталонным результатом. Существуют различные методы выставления баллов за пройденные тесты, однако в общем случае можно говорить о необходимости прохождения (т. е. вывода верного результата) для всех тестов. Также возможен замер каких-либо метрик во время выполнения программы, наиболее распространенными из них являются время работы программы и объем затрачиваемой памяти. В качестве примеров данного подхода можно привести такие автоматические тестирующие системы, как codeforces, acmp, stepik, а также используемые в крупных проектах методологии тестирования (юнит тестирование, тестирование черным ящиком и др.). Преимуществом данного метода является его полный автоматизм, к минусам же можно отнести, во-первых, необходимость создания всеобъемлющего набора тестовых данных, во-вторых, невозможность обнаружения различий для полностью верных решений (решений, прошедших все тесты).
Для нивелирования указанных недостатков тестирования часто используется экспертный анализ. Данный подход заключается в том, что преподаватель (эксперт) самостоятельно просматривает решение ученика и выносит вердикт о качестве решения. Таким образом, при условии, что производится предварительное тестирование программного кода, эксперт оценивает только «верные» решения, что позволяет ему сосредоточиться только на алгоритмических и стилистических ошибках написания программы, а также ошибках в проектировании программного продукта как системы. Естественно, данный подход предоставляет наилучшее на данный момент качество оценивания программного кода. К минусам можно отнести то, что данная процедура требует работы преподавателя и может быть масштабируема только за счет найма дополнительных сотрудников.
Если рассматривать экспертный метод оценивания более детально, то можно говорить о наличии некоторого эталонного решения задачи. В данной интерпретации происходит сравнение решения ученика либо с имеющимся в распоряжении эксперта решением, либо с гипотетическим решением, которое бы данный эксперт реализовал для поставленной задачи. И в самом деле, для большинства автоматических тестирующих систем при создании задачи имеется требование по предоставлению верного решения или решений [2]. Таким образом, можно исходить из того, что для задачи, которую решает обучаемый, имеется написанное на некотором программном языке и полностью верное для всех тестов эталонное решение, т. е. поставленная в исследовании задача об оценивании компетенций обучаемого для построения образовательных траекторий сводится к подзадаче сравнения двух программных кодов.
Прямое посимвольное сравнение программ не приведет к какому-либо значимому результату. Во-первых, это вызвано существованием «незначащих» символов, не являющихся служебными словами языка, слов/символов, которые определил сам пользователь, а также различными числовыми значениями. Например, в программах часто используются «лишние» пробелы, табуляции и переходы на новую строку, разделители команд (точка с запятой и фигурные скобки), комментарии. Однако даже если привести программы к единой стилистике написания, т. е. унифицировать использование незначащих символов до и/или после служебных слов, то вероятность полного совпадения программ все еще будет минимальной. Даже при использовании одного алгоритма существуют вариации в названии переменных, использовании типов данных, очередности вызова операторов. Таким образом, возникает необходимость либо не учитывать указанные различия, либо найти способ значительно снизить их влияние при сравнении двух программ.
Заметим, однако, что это предполагает получение программы, которая, в частности, не имеет последовательности вызова команд, т. е. из нее получается некоторый набор операторов, которые связаны между собой только теми языковыми отношениями, в которые они вступают между собой вне зависимости от своего положения. Например, переменная имеет отношение вхождения с выражениями, в которых она участвует, а также отношение принадлежности с типом данных, которому она принадлежит. Иными словами, получается некоторое подобие семантической сети. В самом деле программный язык все еще является «языком» в обычном понимании, за исключением своей жесткой формализованности. В частности, для него верно то, что его языковые конструкции вступают в отношения со своими соседями и тем самым образуют некий смысл – программу. Это и означает, что вполне возможно построить семантическую сеть по предоставленному программному коду.
В статье [3] уже рассматривался метод построения семантической сети на основе программного кода. Также в ней описывался и возможный метод качественного оценивания полученной сети решения с помощью алгоритмов машинного обучения. Однако данный способ имеет значительные недостатки: для использования алгоритмов машинного обучения необходимо преобразовать семантическую сеть в некоторый массив чисел. Несмотря на то, что в статье приводится метод такого преобразования, он сопряжен с обобщением, а значит и c потерей данных. Также статья не обосновывает выбор конкретного алгоритма машинного обучения. В свете указанных обстоятельств было решено изучить иные способы оценивания качества программного решения, представляемого в виде семантических сетей. Настоящая статья описывает новый алгоритм качественной оценки программного кода, реализованный на языке С++.
Алгоритм сравнения семантических сетей для оценки качества решения задач по программированию
На основе описанного в статье [3] алгоритма были получены две семантические сети – для эталонного программного кода и для оцениваемого решения обучающегося соответственно. Приведем пример получаемой с помощью алгоритма семантической сети (рис.) для программы, печатающей на вывод все четные числа в заданном интервале:
int main()
{
int min, max;
// cin >> min;
// cin >> max;
for (int i = min; i < max + 1; i++)
{
if (i % 2 == 0) /* cout << i << " " */;
}
return 0;
}
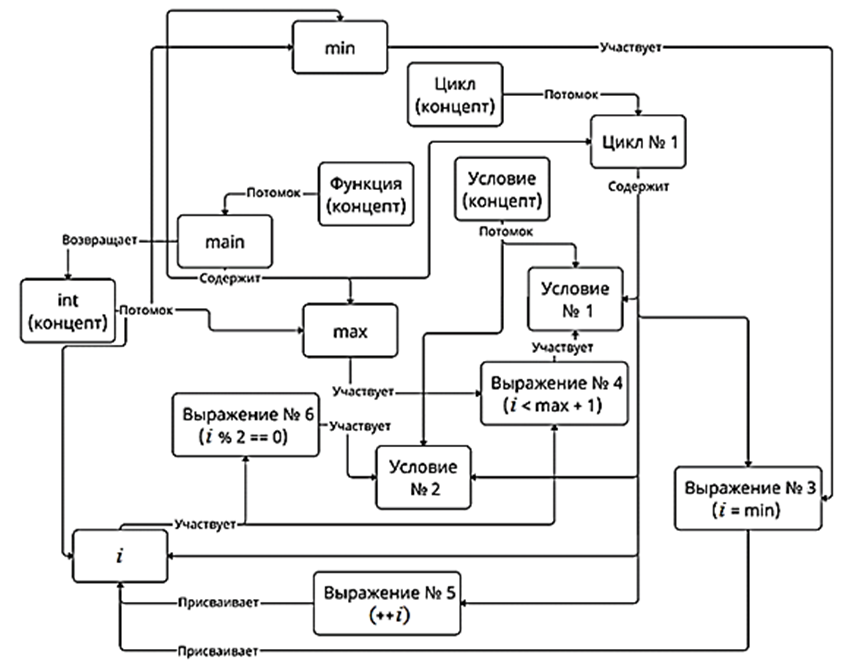
Пример семантической сети на основе программного кода
Example of a semantic network based on source code
Узлы сети, ответственные за ввод и вывод данных, были опущены, чтобы не загружать рисунок. Данные узлы представляют собой очередное выражение (Выражение № 1, Выражение № 2, Выражение № 7), которое связано с соответствующей ему переменной (min, max, i) с помощью соответственного отношения (вводит, вводит, выводит).
В данной сети присутствуют узлы, являющиеся «концептами» языка, т. е. некоторыми базовыми определениями. Также присутствуют узлы, отображающие цикл, условия и функции как некоторый набор содержащихся в них действий (например, узел main содержит узел min). Сами команды программы представлены в узлах «выражение», каждый из которых связан с теми элементами, которые входят в выражение (например, переменная i входит в выражение ++i), либо на которые оно влияет (например, выражение № 6 i % 2 = 0 предоставляет значение условию № 2).
Определим функцию подобия двух семантических сетей, полученных на основе программного кода. Такая функция должна отображать степень похожести двух программ. Одним из наиболее распространенных методов ответа на поставленный вопрос к семантической сети являются алгоритмы поиска на графах. Например, если требуется найти ответ на вопрос о наличии определенного свойства у элемента сети, производится поиск подграфа сети, отвечающего на поставленный вопрос [4]. Однако применение такого метода для расчета функции подобия весьма сомнительно.
Проблема заключается в том, что незначительные изменения программы могут порождать новые узлы или изменять уже имеющиеся таким образом, что сеть не будет совпадать с оригиналом. К таким изменениям можно отнести замену типов данных переменных либо добавление внешнего малозначимого условия. Таким условием может быть проверка введенных значений на принадлежность допустимой области значений. Для учета большой вариативности получаемых графов значение функции подобия должно быть прямо пропорционально количеству одинаковых «элементов» в исследуемых сетях. Самим же элементом будем считать связку узла сети и его ребра. Исходя из алгоритма построения сети [3], узлом графа является концепт языка или программный оператор, а ребром – отношения, в которые вступают упомянутые концепты и операторы. Таким образом, важна не только сама команда в написанной программе, но также и то, как данная операция соотносится с остальным кодом.
Говоря формально, на основе имеющихся сетей требуется получить два подграфа, для которых возможно установить отношение биекции. Тогда само значение функции подобия можно определить как отношение суммы размеров подграфов (полученных для отношения биекции) к сумме размеров изначальных графов (сетей). Отметим, что подграфы для отношения биекции должны получаться путем удаления наименьшего числа изначальных узлов. Данный подход обеспечивает область значения функции в интервале [0; 1], что позволяет проводить удобную конвертацию значения функции в процентное соотношение. Таким образом, функция подобия вычисляется по следующей формуле:
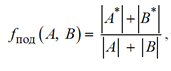 ,
,
где A, B – сети, подаваемые на вход; A*, B* – подграфы, получаемые при построении биекции.
Основываясь на приведенном выше определении функции подобия, можно выделить следующие ее свойства:
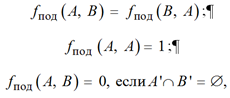
где A', B' – множества, составленные путем перечисления всех элементов сетей A и B соответственно.
Следует отметить, что использование максимального значения размера подграфов не является единственным вариантом. В частности, можно перебрать все варианты пар элементов двух сетей и использовать среднее или медианное значение подобия. Однако поиск всех возможных вариантов сочетаний вершин, во-первых, увеличит асимптотику алгоритма, во-вторых, будет страдать от большого количества вырожденных случаев. Данные вырожденные случаи обеспечиваются жесткой привязкой узлов к своему типу: невозможно построить однозначное соответствие между переменной и функцией или условием и циклом. Соответственно, если пара составлена из узлов разных типов, то биекция невозможна и значение функции подобия равно 0. Само по себе данное явление не является проблемой и выражается в уменьшении области значений итоговой функции. Однако задача, решаемая данной функцией, заключается в сравнении различных программных решений между собой. Чем меньше область значения функции, тем меньше абсолютная разница значений функции при изменении программы. Даже если использовать отношение двух полученных величин функции подобия, точность результата будет страдать тем больше, чем меньше область значений функции подобия.
Для построения взаимно однозначного соответствия можно использовать один из алгоритмов определения изоморфности двух графов, например метод ISD [5]. Как указывает автор метода, для построения отражения графа необходимо для каждой вершины получить уникальный набор характеризующих ее параметров. В случае равнозначности отношений между ребрами необходимо использовать степени вершин графа. Если же отношения графа берутся из некоторого множества, мощность которого больше единицы, то каждому элементу этого множества можно поставить в соответствие уникальную характеристику. На первом шаге алгоритма каждая вершина описывается множеством пар < отношение > – < соседский узел >, которое строится из всех соседей, с которыми соединен текущий узел. Сами пары получаются путем записи характеристики отношения и характеристики вершины (ее порядкового номера). На втором шаге вершина описывается через отношение с соседями своих соседей. Данная рекурсивная процедура продолжается либо до получения набора уникальных характеристик для всех вершин, либо до прекращения изменения набора характеристик при новом шаге алгоритма [6].
Особенностью графов, которые обрабатывает алгоритм сравнения семантических сетей, является то, что узлы графов также имеют свои изначальные характеристики, а именно тип узла. При этом из-за отказа использования порядка следования операторов отсутствует возможность как-либо пронумеровать узлы одинакового типа, а значит они будут равнозначны в исследуемом графе. Также следует отметить наличие различных отношений между ребрами. Степени вершин при этом не могут являться надежной характеристикой
и исключаются из рассмотрения, в самом деле, важно не количество связей для конкретной команды программы, а сами отношения, порождаемые этими связями.
Для использования алгоритма в первую очередь необходимо присвоить каждому виду узлов и отношений свою уникальную характеристику. Отметим, что характеристика узла/ребра является уникальной на всем множестве характеристик (как узлов, так и ребер). В качестве значений характеристик будем использовать простые числа. Выбор простых чисел обусловлен тем, что в базовом алгоритме ISD используется произведение числовых характеристик, а не множество конкретных значений для облегчения вычислений [5]. Используя простые числа, мы гарантируем, что разные виды узлов/отношений не дадут одинаковое произведение.
Как уже отмечалось выше, попытки построения отношений между узлами разных видов бессмысленны. Это означает, что допустимо разбить все узлы графа на отдельные группы по признаку принадлежности к определенному типу, не теряя при этом в точности функции. Данное разбиение условно и не означает разбиение графа на компоненты связности, т. к. необходимо сохранять отношения между вершинами. Тогда задача построения взаимно однозначного соответствия сводится к получению уникальных характеристик для узла только
в той группе, к которой он принадлежит.
Сам алгоритм ISD выполняется только для первого шага. Обоснованием этого является то, что практически все команды программного кода, представленные вершинами, имеют соседним узлом с собой как минимум одну переменную (см. рис.). Это означает, что на втором шаге алгоритма соседом исследуемого узла будет являться вершина типа данных используемой переменной, а также все вершины выражений, в которых участвует данная переменная. На четвертом шаге алгоритма соседями текущего узла будут все команды, содержащие переменные такого же типа данных, например все циклы for, т. к. зачастую данные циклы используют стандартный шаблон объявления счетчика. Все это не приводит к более точному описанию узла через его соседей, а, наоборот, зашумляет его описание. Обобщая изложенное, данная ситуация вызвана малым «расстоянием» от основных концептов языка до любой точки программы (узла сети). Данное расстояние равняется среднему количеству ребер или узлов сети, которое необходимо посетить при переходе от узла, символизирующего команду программы, к узлу концепта языка, если двигаться оптимально. Численно, для выбранных условий построения сети [3], данное значение равняется двум ребрам. Поэтому при увеличении разнообразия отношений между узлами либо при увеличении разнообразия самих узлов количество итераций алгоритма может потребовать пересмотра.
Еще одной проблемой, возникшей при реализации алгоритма, было несоответствие двух узлов, если у обоих имелось по N отношений, из которых совпадающими являются только N – 1 отношений (либо меньше). Таким образом, несмотря на то, что итоговая функция подобия принимает аналоговое значение (на отрезке от 0 до 1), во время ее вычисления для конкретной пары узлов функция подобия, следуя алгоритму ISD, принимает бинарное значение (только 0 или 1), что также снижает чувствительность алгоритма. К примеру, данный эффект возникает, если изменить тип переменной, оставляя остальную программу нетронутой. Чтобы нивелировать описанный эффект, для каждого узла ищется не его точная копия, а наиболее близкий ему по типу и отношениям с соседями узел.
Наконец, можно заметить, что узлы, представляющие собой концепт языка, не несут какую-либо информацию о программе или ее операторах. Они имеют смысл только как соседи других узлов, поэтому узлы с данным типом следует исключить из рассмотрения при расчете значения функции.
Обобщая сказанное, алгоритм для вычисления подобия f (A, B) двух семантических сетей A и B, построенных на программном коде, выглядит следующим образом:
1. Пронумеровать виды узлов и отношений уникальными простыми числами.
2. Описать каждый узел сетей с помощью массива чисел (либо произведением его элементов). Данный массив получается путем обхода соседей выбранного узла и состоит из пар чисел, характеризующих отношение текущего узла с его соседом и тип этого соседа.
3. Сгруппировать для каждой сети полученные вершины по их типу. Исключить из рассмотрения вершины с типом «концепт».
4. Для каждого узла сети A определить наиболее подобный ему узел того же типа из сети B. Подобие двух узлов тем больше, чем больше они имеют одинаковых элементов в их массивах (пары из типа узла и отношения с этим узлом). Значение подобия двух узлов равняется удвоенному количеству одинаковых соседей, поделенному на общее количество всех соседей обоих узлов.
5. Значение функции подобия двух сетей равняется отношению удвоенной суммы значений подобия для каждой вершины графа A к общему количеству вершин в обеих сетях.
Реализация алгоритма
Для проверки работы алгоритм был реализован на языке С++. Исходный код программы выложен по адресу https://github.com/rcomrad/KusOntology. Для изучения были выбраны программы, решающие следующие задачи: поиск максимального элемента в массиве, решение квадратного уравнения, проверка трех чисел на возможность составить из них пифагорову тройку. В табл. 1 и 2 приводятся результаты попарного сравнения базового решения по поиску максимального элемента с другими вариантами решения этой задачи, а также с решениями других задач.
Таблица 1
Table 1
Результат работы алгоритма с различением типов данных
The result of the algorithm with data types distinction
|
Решение |
Конфигурация |
|||
|
Базовая |
С частичным соответствием |
Без учета концептов языка |
Без учета |
|
|
Базовое решение |
1,000 |
1,000 |
1,000 |
1,000 |
|
Изменение используемых типов данных |
0,670 |
0,843 |
0,623 |
0,821 |
|
Добавление внешнего условия |
0,619 |
0,934 |
0,564 |
0,924 |
|
Добавление внешнего условия |
0,430 |
0,789 |
0,349 |
0,759 |
|
Использование иного алгоритма поиска |
0,617 |
0,821 |
0,562 |
0,795 |
|
Изменение способа ввода |
0,925 |
0,992 |
0,914 |
0,990 |
|
Изменение способа ввода и использование |
0,604 |
0,825 |
0,548 |
0,800 |
|
Полностью измененная программа |
0,283 |
0,471 |
0,324 |
0,443 |
|
Программа, возводящая число в квадрат |
0,000 |
0,099 |
0,000 |
0,113 |
|
Программа, решающая квадратное уравнение |
0,050 |
0,176 |
0,057 |
0,169 |
|
Программа, проверяющая стороны треугольника на соответствие теореме Пифагора |
0,000 |
0,155 |
0,000 |
0,145 |
Таблица 2
Table 2
Результат работы алгоритма без различения типов данных
The result of the algorithm without data types distinction
|
Решение |
Конфигурация |
|||
|
Базовая |
С частичным |
Без учета концептов языка |
Без учета |
|
|
Базовое решение |
1,000 |
1,000 |
1,000 |
1,000 |
|
Изменение используемых типов данных |
1,000 |
1,000 |
1,000 |
1,000 |
|
Добавление внешнего условия |
0,585 |
0,908 |
0,516 |
0,892 |
|
Добавление внешнего условия |
0,585 |
0,908 |
0,516 |
0,892 |
|
Использование иного алгоритма поиска |
0,810 |
0,945 |
0,778 |
0,935 |
|
Изменение способа ввода |
0,786 |
0,957 |
0,750 |
0,950 |
|
Изменение способа ввода и использование иного алгоритма поиска максимального элемента |
0,684 |
0,904 |
0,631 |
0,888 |
|
Полностью измененная программа |
0,256 |
0,685 |
0,244 |
0,669 |
|
Программа, возводящая число в квадрат |
0,107 |
0,298 |
0,042 |
0,264 |
|
Программа, решающая квадратное уравнение |
0,114 |
0,483 |
0,067 |
0,475 |
|
Программа, проверяющая стороны треугольника на соответствие теореме Пифагора |
0,057 |
0,475 |
0,000 |
0,465 |
При этом приводятся результаты для 4 возможных модификаций алгоритма:
1. Базовая вариация.
2. Вариация, позволяющая устанавливать частичное соответствие между вершинами.
3. Вариация, не учитывающая узлы графа, являющиеся базовыми концептами языка.
4. Вариация, одновременно не учитывающая базовых концептов языка и позволяющая устанавливать частичное соответствие между вершинами.
Различие между первой и второй таблицами заключается в том, что алгоритм, представленный в первой таблице, оперирует с каждым типом данных как отдельным понятием. Вторая же таблица представляет результат работы алгоритма, для которого типы данных не различаются между собой.
Можно заметить, что значения в столбце «Без учета концептов языка» могут отличаться от значений базовой конфигурации алгоритма как в меньшую, так и в большую сторону. Это объясняется следующим: если сравниваемые программы значительно различаются, то данные узлы будут занижать значение функции. По сути дела, концепты языка будут дублировать отличающиеся отношения языка. И наоборот, при значительной схожести программ данные узлы будут завышать значение функции. Это означает, что алгоритм, не учитывающий концепты языка, позволяет сгладить функцию подобия, убирая перегибы на ее концах. Таким образом, можно говорить о значительной полезности описанной модификации.
Если сравнивать первую и вторую таблицы, то можно было бы ожидать, что значения функции при отсутствии учета различий в типах данных будут выше. Однако это происходит не всегда. По всей видимости, данная модификация позволяет программе находить соответствие между теми узлами, которые не должны были бы совпадать в базовой модификации алгоритма из-за различий в их типах, что приводит к уменьшению значения функции подобия для остальных соседей этих узлов. Описанный подход можно использовать как метод дополнительного анализа программы, если существует вероятность того, что различие в типах данных вносит сильные помехи. Однако для того, чтобы делать предлагаемую вариацию алгоритма основной, полученных при исследовании данных недостаточно.
Если оценивать алгоритм с частичным соответствием, то очевидно, что он вносит огромную составляющую в устойчивость функции подобия к помехам. Особенно хорошо это видно при сравнении базового решения с 3, 7 и 8 вариантами. Можно говорить о том, что данная модификация является критичной для эффективной работы алгоритма.
Заключение
В статье представлен алгоритм вычисления функции подобия для сравнения программного кода решения задач по программированию и ее эталонного решения. Данный алгоритм использует в своей работе преобразование программного кода в семантическую сеть. Для получения значения подобия используется модифицированный алгоритм ISD.
В ходе исследования были рассмотрены различные модификации алгоритма с целью выявления их влияния на конечный результат сравнения.
Основываясь на результатах работы алгоритма, можно говорить о его перспективности в электронных обучающих системах. При этом одним из возможных дальнейших направлений исследования можно назвать изучение того, как множество выделенных концептов языка, а также иные правила вычисления функции подобия для подграфов, могут влиять на результат работы алгоритма.
Следует отметить, что помимо качественного оценивания решения задачи по программированию описанный выше алгоритм позволяет определять степень схожести двух программ. Таким образом, его также возможно использовать для автоматического определения плагиата при проверке ученических решений.
1. Огородникова Е. И. Выстраивание индивидуальных образовательных траекторий // Образование через всю жизнь: непрерывное образование в интересах устойчивого развития. 2012. № 1. С. 219-221.
2. Polygon.CodeForces Tutorial. URL: https://ali-ibra-him137.github.io/competitive/programming/2020/09/27/polygon-codeforces.html (дата обращения: 17.09.2023).
3. Федоров А. С., Шиков А. Н. Метод преобразования семантической сети для автоматизации оценивания решения задач по программированию в процессе электронного обучения // Вестн. Астрахан. гос. техн. ун-та. Сер.: Управление, вычислительная техника и информатика. 2020. № 4. С. 7-17.
4. Родзин С. И., Родзина О. Н. Модели представления знаний. Практикум по курсу «Системы искусственного интеллекта»: учеб. пособие. Таганрог: Изд-во ЮФУ, 2014. 151 с.
5. Погребной В. К. Решение задачи определения изоморфизма графов, представленных атрибутными матрицами // Изв. Том. политехн. ун-та. 2012. № 5. С. 52-56.
6. Погребной В. К. Метод интеграции структурных различий в графовых моделях и его применение для описания структур // Изв. Том. политехн. ун-та. 2011. № 5. С. 10-16.















