Россия
Россия
Россия
Самарская область, Россия
Россия
Россия
С использованием дополнительных граничных условий (ДГУ) и дополнительной искомой функции (ДИФ) получено решение задачи теплопроводности с неоднородными граничными условиями. Дополнительные граничные условия позволяют удовлетворить дифференциальное уравнение на границах, что приводит к его выполнению и внутри области, без интегрирования по декартовой координате. Дополнительная искомая функция сводит исходное уравнение в частных производных к временнóму обыкновенному уравнению, из решения которого определяются собственные числа краевой задачи, определяемые в классических методах из задачи Штурма – Лиувилля, сформулированной в пространственной переменной. Следовательно, в настоящей работе рассматривается иной способ определения собственных чисел. Постоянные интегрирования находятся из начального условия методом наименьших квадратов, позволяющим находить их значения с заданной точностью. Полученное на основе ДГУ и ДИФ решение при n → ∞ приближается к точному аналитическому решению в форме бесконечного ряда, включающего тригонометрические координатные функции с коэффициентами, экспоненциально стабилизирующимися во времени. При этом собственные числа, определяемые из решения временнóго обыкновенного дифференциального уравнения относительно дополнительной искомой функции, в любом приближении совпадают с точными их значениями. Точность выполнения постоянных интегрирования, определяемых методом наименьших квадратов, регулируется числом точек аппроксимации начального условия в диапазоне области изменения пространственной переменной. Отметим, что рассматриваемые в работе дополнительные граничные условия выполняются и при любом другом способе получения решения рассматриваемой задачи, включая и точный метод, в чем можно убедиться непосредственной подстановкой. Следовательно, их введение не искажает исходную математическую постановку задачи, а по- зволяет лишь существенно упростить процесс получения ее аналитического решения.
теплопроводность, граничные условия, дополнительная искомая функция, дополнительные граничные условия, аналитическое решение, метод наименьших квадратов
Введение
В теории теплопроводности применяются методы, связанные с определением интеграла взвешенной невязки исходного дифференциального уравнения, что приводит к его осреднению по пространственной переменной (Л. В. Канторовича, Бубнова – Галеркина, многие разновидности интегрального метода теплового баланса – Т. Гудмена, А. П. Ваничева, М. Био и др.) [1–7]. Все они относятся к группе приближенных аналитических методов, основной проблемой которых является низкая точность получаемых решений. Причина в том, что осреднение дифференциального уравнения по пространственной переменной приводит к низкой точности нахождения собственных чисел, определяющих выполнение дифференциального уравнения. Следовательно, повышение точности связано с увеличением точности выполнения уравнения в области изменения временной и пространственной координат. Для достижения этих целей в настоящей работе используются дополнительная искомая функция (ДИФ) и дополнительные граничные условия (ДГУ) [5, 7]. Их применение не влияет на математическую постановку исходной задачи и является лишь вспомогательным средством упрощения получения ее решения. Следует отметить, что все эти условия выполняются и при любом другом методе получения аналитических решений (включая и классические методы), несмотря на отсутствие их отдельного рассмотрения в процессах получения решений.
Математическая постановка задачи
Найдем решение следующей задачи
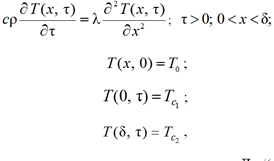
где c – теплоемкость пластины, Дж/(кг·°С); ρ – плотность, кг/м3; T - температура °С ; x – координата, м; τ – время, с; λ – теплопроводность, Вт/(м·К); δ − толщина пластины, м; T0 − начальная температура, К; , − температура пластины, К, при x = 0 и x = δ.
Обозначим
(5)
где Θ, Fo, ξ – безразмерные температура, время (число Фурье), координата соответственно; a = λ / (сρ) – коэффициент температуропроводности тела.
С учетом (5) задача (1)–(4) принимает вид (рис. 1)
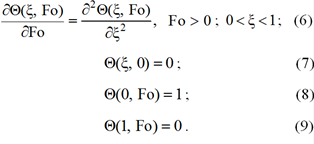
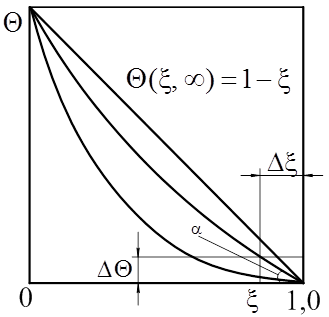
Рис. 1. Схема теплообмена: α – угол наклона
температурной кривой к оси ξ в точке ξ = 1
Fig. 1. Heat exchange diagram: α is the inclination angle
of the temperature curve to the axis ξ at the point ξ = 1
Введем ДИФ q(Fo), характеризующую изменение градиента температуры в точке ξ = 1:
где α(Fo) – угол наклона температурной кривой к оси ξ в точке ξ = 1. Очевидно, что при Fo = 0 tgα = 0, ∂Θ(1, Fo) / ∂ξ = 0. При Fo →∞ tgα → –1, ∂Θ(1, Fo) / ∂ξ = –1.
Реализация метода
Рассмотрим получение решения задачи (6)–(9), приняв его в следующем виде:
, (11)
где bk(q) – неизвестные функции; φk(ξ) = sin(kπξ); 
.
Соотношение (11) удовлетворяет условиям (8), (9). Для нахождения коэффициентов bk(q) используется соотношение (10) и ДГУ, определяемые в граничных точках [5–9]. В работах [7, 8] математически доказывается, что выполнение уравнения в частных производных на границах влечет его выполнение и внутри области, исключая его непосредственное интегрирование, по пространственной переменной.
Найдем ДГУ, которые должны быть выполнены решением (11) в точке ξ = 0 [5, 7]. Дифференцируя условие (8) по Fo, находим
. (12)
Сопоставляя (12) с (6), получаем ДГУ вида
. (13)
Продифференцируем (13) по Fo:
. (14)
Сравнивая (14) и (6), получаем еще одно ДГУ в точке ξ = 0:
.
Аналогично могут быть получены и последующие ДГУ в точке ξ = 0. Общая формула для них имеет вид
(15)
Для получения ДГУ в точке ξ = 1 продифференцируем (9), (10) по Fo:
(16)
(17)
Выражения (16), (17) с учетом (6) приводятся к ДГУ
Продифференцируем (18), (19) по Fo:
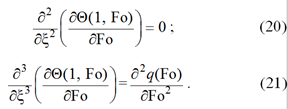
Соотношения (20), (21), учитывая уравнение (6), приводятся к следующим:
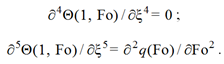
Аналогично можно получить и другие ДГУ в точке ξ = 1. Общие формулы для них
Дополнительные граничные условия, определяемые формулами (15), (22), принятым решением (11) выполняются, что эквивалентно выполнению уравнения (6) в точках
ξ = 0 и ξ = 1 (в предельном смысле – правая и левая его части равны нулю [5, 8]). Следовательно, невыполненными соотношением (11) являются условия (10), (23), которые и будут использованы далее при определении функций bk(q).
В первом приближении, подставляя (11) в (10), находим: bk(q) = (1 + q(Fo)) / π.
С учетом b1(q) соотношение (11) будет
. (24)
В граничных точках ξ = 0 и ξ = 1 соотношение (24) удовлетворяет уравнению (6) в предельном смысле, что не позволяет найти неизвестную функцию q(Fo) из выполнения уравнения (6) в этих точках, в связи с чем потребуем, чтобы соотношение (24) удовлетворяло уравнению (6) в любой из точек переменной (0 < ξ < 1), исключая точки ξ = 0 и ξ = 1. Подставляя (24) в (6), получаем
. (25)
Интеграл уравнения (25) будет
, (26)
где C1 – постоянная интегрирования; v1 = π2 – первое собственное число, равное его точному значению [9, 10].
Подставим (26) в (24):
. (27)
Соотношение (27), независимо от величины C1, точно удовлетворяет граничным условиям (8), (9) и уравнению (6) во всем диапазоне пространственной переменной (0 ≤ ξ ≤ 1), включая точки ξ = 0 и ξ = 1, где оно удовлетворяется в предельном смысле, причем уравнение (6) выполнено, минуя процесс его непосредственного интегрирования по переменной ξ, что можно объяснить выполнением соотношением (27) ДГУ (15), (22). Таким образом, выполнение уравнения внутри области связано с использованием ДГУ и ДИФ. В отличие от классических методов, где собственные числа находятся из решения задачи Штурма – Лиувилля, интегрируемой в области определения пространственной переменной, в данном случае они находятся из решения временно́го обыкновенного дифференциального уравнения, описывающего изменение во времени дополнительной искомой функции.
Постоянная интегрирования C1 находится из выполнения решением (27) начального условия (7) путем использования метода наименьших квадратов. Целью применения этого метода является исключение нахождения сложных интегралов, получающихся в результате выполнения требования ортогональности невязки начального условия ко всем координатным функциям. Использование метода наименьших квадратов позволяет максимально арифметизировать процесс выполнения начального условия, определяя постоянные интегрирования с заданной точностью при сохранении решения в аналитическом виде. При этом процесс выполнения начального условия максимально упрощается, т. к. наиболее трудоемкая часть расчетов, связанных с определением постоянных интегрирования, перекладывается на ЭВМ.
Потребуем выполнения начального условия (7) в следующих 10 точках области: ξi = 0,1; 0,2; 0,3; ...; 0,9; 1,0, (
). Точка ξ = 0 не входит в состав принятых точек ввиду невозможности одновременного выполнения в ней отличающихся друг от друга условий (7) и (8) в начальный момент времени Fo = 0. Подставив (27) в (7) и записав полученное соотношение для 10 выделенных точек, относительно постоянной интегрирования C1 получим систему 10 алгебраических линейных уравнений. Данная система является переопределенной (число уравнений превышает число неизвестных). Найдем ее решение в смысле наименьшего квадратичного уклонения, т. е. используем метод наименьших квадратов. Определяя сумму квадратов начального условия в выделенных точках, получаем следующий функционал:
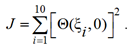. (28)
Подставим (27) в (28):
. (29)
Для нахождения минимума функционала (29) необходимо найти производную по неизвестному C1 и приравнять полученное соотношение к нулю:
(30)
(30)Соотношение (30) представляет алгебраическое уравнение относительно C1. Из его решения находим
. 
(31)
Из (31) находим C1 = 1,98352. Точная его величина составляет C1 = 2,0 [11]. Увеличивая число точек аппроксимации начального условия до 100, для C1 получаем значение, отличающееся от его точной величины лишь в четвертом знаке после запятой (C1 = 1,9998). Однако уже полученная точность при десяти точках аппроксимации вполне достаточна для решения задачи в первом приближении.
Подставляя C1 в (27), получаем первое приближение задачи (6)–(9):
. (32)
Решением (32) точно удовлетворяются уравнение (6) и условия (8), (9) и приближенно – начальное условие (7). Расчеты по формуле (32) в диапазоне
0,1 ≤ Fo ≤ ∞ отличаются от точного решения [12] на 4 %.
Во втором приближении, подставляя (11) в (10), (23) (i = 1) для b1(q) и b2(q), получаем следующие формулы:
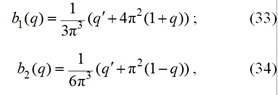
где 
.
Подставим (33) и (34) в (11):
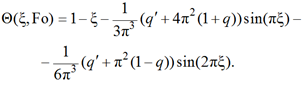(35)
Подставив (35) в (6) и применив полученное соотношение к любой точке переменной ξ (исключая точки ξ = 0 и ξ = 1), находим
,
Интеграл уравнения (36) имеет вид
, (37)
где C1, C2 – постоянные интегрирования; v1 = π2, v2 = 4π2 – собственные числа, равные точным их значениям [12].
Подставим (37) в (35):
(38)
Соотношение (38), независимо от величин C1 и C2, точно удовлетворяет граничным условиям (8), (9) и уравнению (6) во всем диапазоне изменения временно́й и пространственной переменных, включая точки ξ = 0 и ξ = 1. Выполнение уравнения (6) во всем диапазоне пространственной переменной, минуя процесс непосредственного интегрирования по ней, является следствием того, что соотношение (38) точно удовлетворяет ДГУ (15), (22), (23). Отметим, что эти условия выполняются n при любом другом методе получения решения задачи (6)–(9), – отличие лишь в том, что они не выделяются в них в качестве условий для отдельного рассмотрения.
Для определения постоянных интегрирования C1 и C2, аппроксимируя начальное условие в 100 точках области (0 < ξ < 1), получаем переопределенную систему 100 алгебраических уравнений с неизвестными C1 и C2. Используя метод наименьших квадратов, получаем: C1 = 1,9998; C2 = –1,9998. Полученные величины C1 и C2 в пятом знаке после запятой отличаются от точных их значений. Точность определения C1 и C2 можно повысить, увеличивая число точек аппроксимации начального условия. В дальнейшем будем считать, что постоянные интегрирования найдены с точностью до пятого знака после запятой (по сравнению с точными их значениями), и записывать в решения точные значения C1 и C2. Соотношение (38) с учетом C1 и C2 будет
(39)
Соотношение (39) представляет второе приближение задачи (6)–(9). Оно точно удовлетворяет уравнению (6), граничным условиям (8), (9) и приближенно – начальному условию (7). Расчеты по формуле (39) в диапазоне 0,1 ≤ Fo ≤ ∞ отличаются от точного решения [12] на 1 %.
В третьем приближении неизвестные b1(q), b2(q), b3(q)) находятся из (10), (23) (при i = 1, 2). Из решения системы 3-х алгебраических уравнений для них получены следующие формулы:
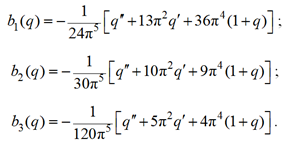
Подставляя (11) (с учетом b1(q), b2(q), b3(q)) в уравнение (6) и применяя полученное соотношение для любой точки переменной ξ (исключая точки ξ = 0 и ξ = 1), получаем
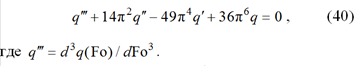
Интеграл уравнения (40) будет
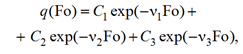
где v3 = 9π2 – третье собственное число, равное его точному значению [12]; C1, C2, C3 – постоянные, определяемые из (7). Аппроксимируя (7) в 100 точках пространственной переменной ξ (исключая точку ξ = 0) и используя метод наименьших квадратов, получаем их значения, совпадающие с точными до четвертого знака после запятой. Учитывая, что точность определения C1, C2, C3 можно повысить (путем увеличения числа точек аппроксимации начального условия), далее будем использовать их точные значения, равные C1 = 2, C2 = –2, C3 = 2.
С учетом полученных bk(q), функции q(Fo) и C1, C2, C3 решение в третьем приближении принимает вид
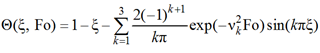,(41)
где vk = kπ.
Формула (41) справедлива и в последующих приближениях k = 1, 2, 3, ..., n. Общая формула для них будет
(42)
Соотношение (42) при n → ∞ совпадает с классическим точным аналитическим решением задачи (6)–(9) [12]. Расчеты по формуле (42) в различных приближениях приведены на рис. 2.
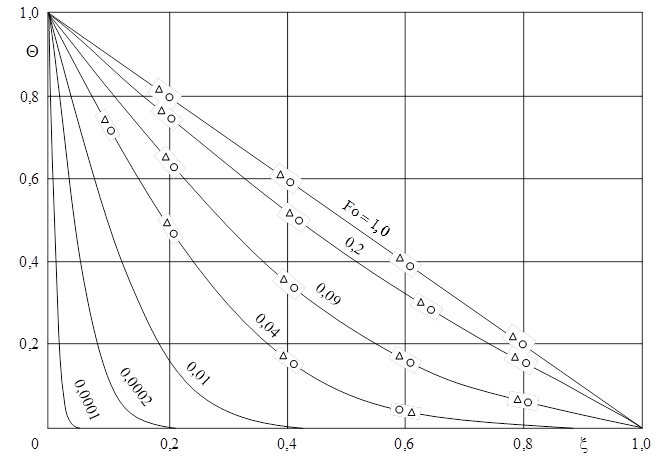
Рис. 2. Изменение температуры: – 1-е приближение;
– 2-е приближение;
– точное решение [12]
Fig. 2. Temperature changes: – 1st approximation;
– 2nd approximation;
– exact solution [12]
Приближение к формуле для коэффициентов Ak с заданной точностью выполняется методом наименьших квадратов.
Заключение
Путем использования ДГУ и ДИФ получено решение задачи теплопроводности для пластины с неоднородными граничными условиями первого рода, приближающееся точному решению при n → ∞. Применение ДГУ позволяет выполнить исходное уравнение во всей области пространственной переменной без проведения непосредственного интегрирования по ней, в связи с чем процесс получения аналитического решения сводится лишь к интегрированию обыкновенного уравнения относительно ДИФ (изменяющейся лишь во времени), из которого находятся собственные числа, определяемые в классических методах из задачи Штурма – Лиувилля, заданной в пространственных переменных. Следовательно, в настоящей работе приводится другой способ определения собственных чисел, основанный на решении временного уравнения для ДИФ.
Постоянные интегрирования находятся путем выполнения начального условия методом наименьших квадратов, позволяющим находить их значения практически с заданной точностью. Преимущество такого способа их определения заключается в отсутствии необходимости нахождения интегралов в пределах области изменения пространственной переменной при сохранении аналитического вида решения.
1. Беляев Н. М., Рядно А. А. Методы нестационарной теплопроводности. М.: Высш. шк., 1978. 328 с.
2. Био М. Вариационные принципы в теории тепло-обмена. М.: Энергия, 1975. 208 с.
3. Глазунов Ю. Т. Вариационные методы. М.; Ижевск: НИЦ «Регулярная и хаотическая динамика»; Ин-т компьютер. исслед., 2006. 470 с.
4. Гудмен Т. Применение интегральных методов в нелинейных задачах нестационарного теплообмена // Проблемы теплообмена: сб. науч. тр. М.: Атомиздат, 1967. С. 41-96.
5. Кудинов В. А., Еремин А. В., Трубицын К. В., Стефанюк Е. В. Модели термомеханики с конечной и бесконечной скоростью распространения теплоты. М.: Проспект, 2020. 224 с.
6. Кудряшов Л. И., Меньши́х Н. Л. Приближенные решения нелинейных задач теплопроводности. М.: Машиностроение, 1979. 232 с.
7. Кудинов И. В., Котова Е. В., Кудинов В. А. Метод получения аналитических решений краевых задач на основе определения дополнительных граничных усло-вий и дополнительных искомых функций // Сибирский журнал вычислительной математики. 2019. Т. 22, № 2. С. 153-165.
8. Федоров Ф. М. Граничный метод решения прикладных задач математической физики. Новосибирск: Наука, 2000. 220 с.
9. Канторович Л. В. Использование идеи метода Галеркина в методе приведения к обыкновенным дифференциальным уравнениям // Прикладная математика и механика. 1942. Т. 6, № 1. С. 31-40.
10. Канторович Л. В., Крылов В. И. Приближенные методы высшего анализа. Л.: Физматгиз, 1962. 708 с.
11. Карташов Э. М. Аналитические методы в теории теплопроводности твердых тел. М.: Высш. шк., 2001. 550 с.
12. Лыков А. В. Теория теплопроводности. М.: Высш. шк., 1967. 600 с.
