Россия
Рассматривается проблема применения цифрового водяного знака на основе метода дискретных вейвлет- и косинусного преобразований к полноцветному изображению. Данный метод представляет собой процедуру внедрения метки в частотную область цифрового изображения, в алгоритме которого используется определенный коэффициент усиления. Представлены общие сведения об алгоритме и его составляющих. Описано влияние усиливающего коэффициента на эффективность внедрения и извлечения водяного знака и степень искажения обрабатываемого изображения. Проведены исследования этих зависимостей с целью нахождения оптимального спектра (коэффициента) цифрового цветового пространства для внедрения скрытой метки в полноцветное изображение с оптимальным значением коэффициента усиления. Для измерения степени эффективности извлечения был использован коэффициент линейной корреляции Пирсона, а для измерения степени искажения – метрика индекса структурного сходства цифровых изображений. Были выявлены спектры, наиболее пригодные в качестве носителя цифрового водяного знака, а также оптимальные значения усиливающего коэффициента для этих спектров. Использование оптимального коэффициента не приводит к значительным искажениям изображения, при этом обладая достаточной эффективностью извлечения водяного знака.
цифровой водяной знак, защита авторских прав, изображение, дискретные преобразования, система человеческого зрения, искажение
Введение
В связи с колоссальной скоростью развития информационных технологий и средств передачи информации возможности распространения медиаконтента стали чрезвычайно простыми и в то же время массовыми [1], поэтому вопрос о защите авторских прав стал еще острее.
Цифровые водяные знаки (ЦВЗ) являются эффективным методом защиты авторских прав на цифровые изображения. Этот метод предполагает встраивание информации, такой как уникальный идентификатор или имя автора, в само изображение таким образом, что изменения остаются незаметны для системы человеческого зрения (СЧЗ). Целью применения ЦВЗ является предоставление доказательств авторства в случае споров на предмет авторского права оспариваемого изображения, а также защита от несанкционированного копирования и распространения при передаче изображений через сеть [2, 3]. Сам термин «цифровой водяной знак» впервые был приведен в работе [4], авторы которой предложили два стеганографических метода сокрытия информации в изображении, с тех пор ЦВЗ активно развиваются.
Система ЦВЗ включает в себя подсистемы встраивания и извлечения ЦВЗ [5], общая схема представлена на рис. 1.

Рис. 1. Общая схема системы ЦВЗ: SE – помеченное изображение;
SEm – помеченное изображение, подвергнувшееся возможной модификации
Fig. 1. General scheme of the digital watermark system: SE – watermarked image;
SEm – labeled image that has been possibly modified
Цифровой водяной знак может быть робастным (стойким), полухрупким и хрупким [6]. Хрупкий ЦВЗ восприимчив к большинству изменений контейнера, после которых его невозможно извлечь. Такой тип ЦВЗ обычно используется в целях проверки целостности изображения. Полухрупкий ЦВЗ разрушается только от определенных изменений изображений, зависящих от алгоритма встраивания. Стойкие ЦВЗ переносят различные виды атак, и именно они в большинстве случаев используются как метод защиты авторских прав.
Алгоритмы водяных знаков можно разделить на две основные категории: встраиваемые в пространственную область и встраиваемые в области преобразования. В первом случае встраивание производится в само изображение, а именно изменяются конкретные пикселы в зависимости от алгоритма. Вторая группа методов производит «перераспределение энергии» изображения перед самим алгоритмом встраивания, что позволяет достичь лучшей стойкости в ущерб ресурсозатратности.
В данной статье будет рассмотрен один из робастных алгоритмов ЦВЗ, сочетающий в себе преимущества дискретного вейвлет-преобразования (ДВП) и дискретного косинусного преобразования (ДКП). Данный метод имеет преимущества перед методами, использующими эти преобразования по отдельности, а именно обладает большей робастностью к применению шума к изображению, его сжатию и его обрезанию [7].
В алгоритме внедрения присутствует усиливающий коэффициент, определяющий силу внедрения ЦВЗ. Выбор значения этого коэффициента является непростым, т. к. при его высоких значениях изображение подвергается сильному искажению, а при низких снижается эффективность извлечения. Кроме того, при встраивании ЦВЗ в полноцветное изображение также появляется фактор, влияющий на выбор усиления, а именно выбор спектра цвета изображения, в который необходимо встраивать водяной знак. Происходит это из-за того, что СЧЗ по-разному восприимчива к каждому из видимых цветов.
В настоящей статье рассмотрено влияние коэффициента усиления алгоритма ЦВЗ, основанного на ДВП-ДКП, на степень искажения и эффективность ЦВЗ с учетом специфики полноцветного изображения. Похожие исследования проводились только для полутоновых цифровых изображений и не затрагивали особенности полноцветных [8, 9]. В монотонных изображениях влияние коэффициента усиления на степень искажения значительно ниже, поэтому в них коэффициент может принимать гораздо большие значения, чем при использовании к полноцветному. Помимо этого, в этих работах для определения уровня искажений изображения вследствие внедрения ЦВЗ использовалась метрика PSNR (пиковое отношение сигнала к шуму), не учитывающая структурное сходство изображений и особенностей СЧЗ.
Описание преобразований, использующихся в алгоритме
Прежде чем переходить к исследованиям, необходимо обозначить основные принципы и алгоритмы преобразований, использующихся в данном методе ЦВЗ.
Дискретное косинусное преобразование – метод преобразования входящего сигнала на элементарные частотные коэффициенты. Применяемое
к изображению, оно представляет его как сумму синусоид различных амплитуд и частот. Допустим, входное квадратное изображение X имеет размер
N × N пикселов, тогда изображение Y размером N × N пикселов, которое образовывается в результате применения ДКП, можно получить следующим образом:

где i, j – частотные координаты в области преобразования; n, m – пространственные координаты пиксела исходного изображения; α(i)

Обратное преобразование происходит следующим образом:
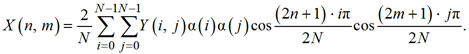
Результатом преобразования является матрица коэффициентов изображения. В левом верхнем углу матрицы находится так называемый DC-коэффи-
циент, содержащий в себе наибольшую информацию об энергии изображения. Соответственно, в левом верхнем углу находятся низкочастотные коэффициенты, несущие в себе основную информацию об изображении, в правом нижнем углу – высокочастотные коэффициенты, содержащие в себе информацию о незначительных деталях, как правило, близкие к нулю. Между ними находятся среднечастотные коэффициенты. Встраивание битов ЦВЗ производится именно в область средних частот, т. к. изменение низких ведет к заметному искажению изображения, а высокие отбрасываются при сжатии изображения.
Как правило, ДКП применяется не ко всему изображению сразу, а поблочно, обычно к квадратным матрицам размерностью 4, 8 или 16 пикселов. В исследуемом методе ДКП применяется поблочно к матрицам 4 × 4 пикселов.
Дискретное вейвлет-преобразование. Под ДВП понимается целый ряд преобразований, основанных на использовании различных семейств вейвлет-функций [10]. В алгоритме используется вейвлет Хаара. Суть вейвлета Хаара состоит в следующем.
Пусть имеется входной сигнал, представляющий собой массив S(i1, i2, ..., iN) длины N. При применении к нему ДВП Хаара каждой паре соседних элементов ставятся в соответствие два новых числа [9]:

где i = 1, 2, …, N / 2; S2i–1 и S2i – элементы входного сигнала под соответствующими индексами.
В результате получается пара сигналов, первый из которых содержит в себе грубую версию первоначального (среднее значение каждой пары элементов S) и называется аппроксимацией. Второй сигнал содержит в себе детализирующую информацию, представляющую собой значение отклонения получившегося и изначального сигнала и необходимую для восстановления исходного. Обратное преобразование имеет следующий вид:

Пока остается как минимум одна пара аппроксимирующих коэффициентов, ДВП Хаара может быть применима к ним снова и снова, что разбивает входной массив на низкие, средние и высокие частоты. В результате наибольшие по абсолютной величине коэффициенты располагаются в области низких частот, наименьшие – в области высоких.
Применительно к изображениям используется двумерное ДВП, являющееся композицией одномерных преобразований. Полученные в результате матрицы принято обозначать LL, HL, LH, HH частотными поддиапазонами. Квадрат LL содержит в себе низкочастотные коэффициенты и очень похож на исходное изображение, остальные содержат в себе высокочастотные коэффициенты. К получившимся поддиапазонам можно также применять ДВП. В результате могут получаться многоуровневые матрицы ДВП (рис. 2).

Рис. 2. Поддиапазоны ДВП при одноуровневом ДВП (а); двухуровневом ДВП, примененном к HL1 (б)
Fig. 2. DWT sub-bands at: single level DWT (а); two-level DWT applied to HL1 (б)
В настоящем методе ЦВЗ метка вставляется в поддиапазон HL2 второго уровня ДВП, примененного к HL1.
В общих чертах алгоритм внедрения представлен на рис. 3.

Рис. 3. Общий вид алгоритма внедрения ЦВЗ
Fig. 3. General view of the digital watermark implementation algorithm
Подробно алгоритм рассматривается в [8]. Если необходимо обеспечить более высокий уровень безопасности, вместо преобразования Арнольда можно использовать алгоритм шифрования. Процесс извлечения очень похож на процесс внедрения, в нем для получения ЦВЗ из изображения используется коэффициент корреляции Пирсона. Само встраивание ЦВЗ производится в среднечастотные коэффициенты ДКП.
Помимо стандартного цветового пространства RGB (red, green, blue), где каждый компонент представляет собой значение насыщенности соответствующего цвета, в исследовании используется цветовое пространство YCbCr (значения яркости, насыщенности синего и красного). В нем, в отличие от RGB, яркость отделяется от цветовых составляющих изображения. Система человеческого зрения менее чувствительна к изменению цвета какого-либо предмета, нежели к изменению его яркости [11]. Компоненты Cb и Cr несут в себе гораздо меньше информации об изображении, чем коэффициент Y. Помимо этого, человеческий глаз наименее восприимчив именно к красному и синему цветам, т. к. они находятся на границах видимого человеком спектра излучения. Эти факты играют на пользу цветового пространства YCbCr в области применения ЦВЗ.
Необходимо провести исследования зависимости степени искажения и эффективности работы ЦВЗ от коэффициента усиления. Так как уровень искажений изображения и эффективность ЦВЗ увеличиваются с нарастанием усиления, необходимо выбрать его оптимальное значение, при котором эффективность извлечения ЦВЗ будет находиться на достаточном уровне, а искажения изображения не заметны для СЧЗ. Исследование будет проводиться со всеми шестью коэффициентами выбранных ранее цветовых пространств, а именно RGB и YCbCr.
Исследование зависимости уровня искажения и эффективности извлечения от усиления
Влияние коэффициента усиления на эффективность извлечения. Для уменьшения погрешностей возьмем для исследования 5 растровых полноцветных изображений («Лена», портрет Наполеона, фотография Мачу-Пикчу, «Черный квадрат», «Звездная ночь») размером 512 × 512 пикселов. К каждому из них применим процедуру внедрения ЦВЗ с коэффициентом усиления от 1 до 12, после чего извлечем ЦВЗ и сравним с оригиналом. Полученную информацию можно представить на графике, где оси обозначаются усилением и коэффициентом схожести соответственно. Схожесть можно проверить с помощью линейной корреляции Пирсона по следующей формуле:

где xi, yi – элементы выборки; n – размер выборки.
Коэффициент принимает значения от –1 до +1. Значение 0 говорит об отсутствии корреляции, а значит и отсутствии линейной связи между переменными. Величина коэффициента +1 показывает, что значения параметров коррелируют напрямую, и при увеличении одного параметра увеличивается и другой. При значении –1 ситуация обратная – если одна величина увеличивается, то другая уменьшается. Таким образом, чем выше коэффициент корреляции, тем увереннее можно утверждать, что извлеченный ЦВЗ является оригинальным.
Результаты исследования представлены на рис. 4.

Рис. 4. График зависимости точности извлечения от усиливающего коэффициента
Fig. 4. Graph of the extraction accuracy depending on the amplifying coefficient
На каждом шаге усиления вычислялись коэффициенты для всех 5 изображений, после чего находились средние значения.
Как заметно по графику, спектры Cb и Cr палитры YCbCr показывают значительно лучшие результаты, чем остальные. Зависимость точности извлечения спектров Y палитры YCbCr и R, G, B палитры RGB находится практически на одном уровне. Как и ожидалось, зависимость эффективности извлечения ЦВЗ и коэффициента усиления является линейной: чем выше усиление, тем выше эффективность. Однако при этом увеличивается
и степень искажений изображения, которую мы рассчитаем далее.
Влияние усиливающего коэффициента на степень искажения изображения. Для измерения степени искажения изображения существует довольно большой выбор количественных метрик. Такие метрики позволяют сравнить два изображения на предмет их сходства и получить его количественную характеристику. В основном эти метрики используются для проверки качества сжатия цифрового изображения, однако они могут помочь и определить степень искажения изображения при встраивании в него ЦВЗ. Наиболее часто используемыми метриками являются MSE (среднеквадратическая ошибка), PNSR (пиковое отношение сигнала к шуму) и SSIM (индекс структурного сходства).
В статьях [8, 9] для измерения степени искажения используется метрика PSNR, однако она не учитывает структурные различия изображений и несовместима с физиологией человеческого восприятия, т. к. учитывает лишь разницу между двумя пикселами. Этот недостаток исправляет метрика SSIM, являющаяся более комплексной и эффективной по сравнению с PSNR.
Метрика SSIM обеспечивает более точную оценку сходства двух изображений по сравнению с другими метриками. Принцип метрики заключен в его названии – она учитывает структурное сходство между двумя изображениями, проверяя схожесть поблочно. Выходным значением, как правило, является число между 0 и 1, где 1 означает абсолютную схожесть сравниваемых изображений.
Исследование проводится с теми же изображениями и в тех же условиях. Результаты представлены на рис. 5.

Рис. 5. График зависимости коэффициента SSIM от усиления
Fig. 5. Graph of the SSIM coefficient depending on the gain
Основываясь на результатах, можно заключить, что встраивание ЦВЗ в коэффициенты Y из палитры YCbCr и G из RGB приводит к наибольшим искажениям изображений. Происходит это из-за разной степени чувствительности СЧЗ к различным компонентам изображения, как было отмечено ранее, изменение яркости человек замечает лучше, чем изменение цвета. В случае со спектром G высокая степень искажения объясняется тем, что СЧЗ более чувствительна к зеленому цвету, чем к синему или красному. Рассматривая оставшиеся коэффициенты, можно заметить, что их зависимость искажения от усиления отличается незначительно. Таким образом, наилучшими спектрами для внедрения ЦВЗ являются Cb и Cr палитры YCbCr. Они искажают изображение не сильнее, чем остальные коэффициенты, однако эффективность извлечения ЦВЗ для этих спектров значительно выше по сравнению с другими спектрами. Например, при усиливающем коэффициенте, равном 3, спектры Cb и Cr дают точность 0,8 и 0,86 соответственно, в то время как другие не дотягивают и до 0,5.
Заключение
Таким образом, оптимальными спектрами для внедрения ЦВЗ являются Cb и Cr палитры YCbCr. Именно эти два коэффициента показывают наилучшую степень эффективности извлечения ЦВЗ, не создавая при этом больше искажений, чем другие спектры, согласно метрике SSIM. При этом оптимальное значение усиливающего коэффициента при встраивании ЦВЗ в эти спектры может находиться в диапазоне от 3 до 6. При этом от встраивания ЦВЗ в коэффициенты Y палитры YCbCr и G палитры RGB следует отказаться ввиду значительного искажения изображения.
1. Сурин В. А., Тырсин А. Н. Применение обобщенного метода наименьших модулей в задачах обработки и анализа изображений // Вестн. Астрахан. гос. техн. ун-та. Сер.: Управление, вычислительная техника и информатика. 2020. № 2. С. 45-55.
2. Sanivarapu P. V., Rajesh K. N. V. P. S., Hosny K. M., Fouda M. M. Digital Watermarking System for Copyright Protection and Authentication of Images Using Cryptographic Techniques // Appl. Sci. 2022. V. 12 (17). P. 8724. URL: https://doi.org/10.3390/app12178724 (дата обращения: 15.03.2023).
3. Hosny K. M., Darwish M. M. Invariant image water-marking using accurate polar harmonic transforms // Comput. Electr. Eng. 2017. V. 62. P. 429-447. URL: https://www.sciencedirect.com/science/article/abs/pii/S004579061630550X?via%3Dihub (дата обращения: 15.03.2023).
4. van Schyndel R. G., Tirkel A. Z., Osborne C. F. A digital watermark // In Proceedings of the IEEE 1st Interna-tional Conference on Image Processing. Austin, TX, USA, 1994. V. 2. P. 86-90.
5. Федосеев В. А. Цифровые водяные знаки и стеганография. Самара: Изд-во Самар. ун-та, 2019. 144 с.
6. Tsougenis E. D., Papakostas G. A., Koulouriotis D. E., Tourassis V. D. Performance evaluation of moment-based watermarking methods // Jour. of Sys. And Soft. 2012. V. 85, iss. 8. P. 1864-1884.
7. Ali Al-Haj. Combined DWT-DCT Digital Image Wa-termarking // Journal of Computer Science. 2007. P. 740-746.
8. Saeed F., Golestanian M., Azimi M. A Blind Water-marking Algorithm Based On DCT-DWT and ARNOLD Transform // International Journal of Computer Science Engineering (IJCSE). 2013. V. 2, no. 06. P. 328-334.
9. Бахрушина Г. И., Коржавин В. А. Использование дискретных преобразований при разработке устойчивых алгоритмов цифрового маркирования изображений // Электронное научное издание «Ученые заметки ТОГУ». 2016. Т. 7, № 4. С. 7-24.
10. Сэломон Д. Сжатие данных, изображений и звука. М.: Техносфера, 2004. 368 с.
11. Ричардсон Я. Видеокодирование. Н.264 и MPEG-4 - стандарты нового поколения. М.: Техносфера, 2005. 368 с.















