Россия
Москва, Россия
Россия
студент
Москва, Россия
Рассмотрен переходной режим работы оптического коммутатора, описанного с помощью модели одноканальной системы массового обслуживания с ограниченным буфером, пуассоновским входным потоком и экспоненциальным распределением времени обслуживания. Для решения системы уравнений Колмогорова и нахождения вероятностей состояний в переходном режиме использован аппарат преобразования Лапласа. Найдены аналитические выражения для определения вероятности потерь и пропускной способности оптического коммутатора в заданный момент времени. В численном примере проанализированы характеристики производительности оптического коммутатора с размером буфера, равным двум пакетам, при различной за-грузке сети в переходном и стационарном режимах. Стационарные характеристики, полученные с использо-ванием предлагаемого подхода, совпали с известными результатами, что подтверждает корректность выводов. Найденные значения времени переходного режима при различной загрузке сети показали, что при уменьшении
оптический коммутатор, переходной режим, системы массового обслуживания, преобразование Лапласа, вероятности состояний, пропускная способность
Введение
С развитием оптических сетей нового поколения повысился интерес к их моделированию. В большинстве случаев для этого используется математический аппарат теории массового обслуживания [1, 2]. В зависимости от параметров оптических сетевых устройств для описания их работы могут использоваться различные типы систем массового обслуживания (СМО). По числу каналов такие СМО можно разделить на однолинейные системы [3], имеющие только одно обслуживающее устройство, и многолинейные системы, в которых потоки требований распределяются между некоторым количеством обслуживающих устройств [4]. По наличию очереди СМО подразделяют на системы с бесконечным или конечным буфером.
Характеристики производительности СМО, такие как размер буфера, количество заявок в системе, вероятность потерь, время ожидания заявки в очереди, могут быть описаны как в стационарном [4, 5], так и в переходном режиме [6–10]. При этом в стационарном или, другими словами, установившемся режиме характеристики системы не зависят от времени. Переходной режим достигается через некоторое время после начала функционирования системы или ее перезапуска и продолжается в течение некоторого времени до перехода в стационарный режим. Такие режимы также возникают при резком увеличении потока заявок в системе или внезапном выходе из строя обслуживающего устройства.
Следует отметить, что на сегодняшний день большая часть исследований СМО и поиск их характеристик производительности проводятся в стационарном режиме [1, 4]. Например, в работе [4] исследуется многолинейная СМО с резервными приборами и ограниченными очередями на каждом приборе, на вход которой поступает коррелированный групповой BMAP-поток. Для данной системы найдено стационарное распределение вероятностей состояний системы и проведен анализ основных характеристик ее производительности, таких как среднее число заявок в системе, среднее число занятых приборов и вероятность потери заявок.
Однако с повышением пропускной способности сетей связи нового поколения, переходом на полностью оптические системы [11] длительность переходного режима становится сравнимой с длительностью оптического пакета. В связи с этим разработка модели для расчета вероятности потерь пакетов и других характеристик производительности оптических коммутационных устройств в нестационарном режиме позволит оператору связи формулировать правильные и более точные требования к техническим характеристикам коммутационного оборудования, что приведет к повышению качества предоставляемых услуг.
Оценка продолжительности переходного режима в зависимости от параметров входного потока и характеристик обслуживающего устройства позволяет оптимизировать работу системы в переходном режиме, минимизировать его влияние на работу системы в целом и является важной задачей при проектировании систем связи.
Несмотря на проявляемый интерес в последнее время к переходному режиму СМО, в большинстве работ отсутствуют численные результаты анализа ее переходных характеристик [7], и лишь в ряде работ они получены с использованием численных методов [6, 8, 9]. Так, в работе [8] при исследовании СМО, на вход которой поступает поток с интенсивностью облуживания, имеющей распределение Эрланга, полученные выражения для различных показателей производительности системы в переходном режиме (ожидаемое количество клиентов в очереди, время ожидания обслуживания, ожидаемое количество заявок в очереди) содержат неизвестные вероятности состояний системы, вычисляемые с использованием численного метода Runge-kutta.
Наличие аналитических выражений для основных характеристик СМО в переходном режиме является важным для анализа их работы и необходимым при решении задач синтеза таких систем.
В данной работе исследуется модель оптического коммутатора с ограниченным буфером и проводится анализ его характеристик в переходном режиме с использованием аналитического метода, основанного на аппарате преобразования Лапласа; представлен граф состояний системы и описана постановка задачи; рассматривается аналитический метод решения уравнений Колмогорова, описывающих работу заданной системы в переходном режиме; приведены численные расчеты основных характеристик производительности оптического коммутатора.
Постановка задачи
В данной работе рассматривается модель оптического коммутатора в переходном режиме, которая представляет собой СМО M/M/1/N, на вход которой поступает простейший поток заявок с интенсивностью λ, а время обслуживания заявок имеет показательное распределение с параметром μ. Когда прибор занят, заявка поступает в буфер, если в нем имеется свободное место. Если все N мест для ожидания в буфере заняты, то заявка покидает систему необслуженной (теряется). Граф состояний рассматриваемой СМО представлен на рис. 1.
Рис. 1. Граф состояния системы M/M/1/N:
S0 – начальное состояние, при котором в системе отсутствуют заявки; S1 – одна заявка обрабатывается обслуживающим устройством, буфер свободен; S2 – одна заявка обрабатывается обслуживающим устройством, и одна заявка находится в буфере; Sn –одна заявка обрабатывается обслуживающим устройством, n заявок находится в буфере;
SN + 1 – одна заявка обрабатывается обслуживающим устройством, буфер полностью заполнен, вновь поступившая заявка теряется
Fig. 1. Graph of the state of system M/M/1/N:
S0 – initial state at which the system has no orders; S1 – one order is processed by the server, the buffer is free;
S2 – one order is processed by the server and one order is in the buffer; Sn – one order is processed by the server and n order
is in the buffer; SN + 1 – one order is processed by the server,
the buffer is full, the newly received order is lost
Уравнения Колмогорова, описывающие работу данной системы, имеют вид
(1)
где – вероятность n-го состояния системы
в момент времени t, соответствующая вероятности нахождения в системе n пакетов, таким образом, P0(t) – вероятность того, что в системе отсутствуют заявки, PN - 1(t) – вероятность того, что в системе находятся N – 1 пакетов, PN + 1(t) – вероятность того, что буфер заполнен полностью, следующий поступивший пакет теряется, что соответствует вероятности потери пакетов.
Требуется разработать аналитическую модель оптического коммутатора с ограниченным буфером, позволяющую анализировать вероятности состояний его работы и характеристики его производительности как в стационарном, так и в переходном режиме.
Описание аналитического метода
Для решения системы уравнений (1) будем использовать аппарат преобразования Лапласа [1, 12], что позволяет свести систему дифференциальных уравнений (1) к системе линейных алгебраических уравнений и значительно упростить ее решение. Для начала запишем систему (1) в матричном виде:
, (2)
где 
– вектор вероятностей состояний; B – матрица коэффициентов дифференциальных уравнений системы (1).
После применения преобразования Лапласа к системе (2) 
и, используя свойство дифференцирования оригинала 
, где s – комплексная переменная; 
– изображения вектора вероятностей состояний; 
– вектор начальных условий, перепишем (2) в следующем виде:
.
Таким образом, получим неоднородную систему линейных алгебраических уравнений
(3)
где I – единичная диагональная матрица.
Запишем (3) в виде
, (4)
где 
.
Решая систему (4) методом Крамера, получим вектор изображений вероятностей состояний системы 
, k-й элемент которого равен
,
где 
– определитель матрицы 
; 
– определитель матрицы 
, полученной путем замены k-го столбца матрицы вектором начальных условий .
Таким образом, решением системы (4) являются операторные выражения вероятностей k-х состояний системы 
, представляющие собой дроби, в числителе и знаменателе которых стоят степенные полиномы и соответственно. Для перехода к оригиналам 
будем использовать формулу разложения [12], согласно которой окончательные выражения для вероятностей
k-состояний системы в переходном режиме будут иметь вид
, (5)
где n – общее число состояний системы.
Характеристики производительности оптического коммутатора в переходном режиме
Рассмотрим основные характеристики производительности оптического коммутатора в переходном режиме
Вероятность потери пакетов. Вероятность потери пакетов равна вероятности состояния системы 
, когда обслуживающее устройство занято и буфер коммутатора заполнен полностью. В данном состоянии системы вновь поступивший пакет отбрасывается. Таким образом, выражение для вероятности потери пакетов имеет вид
(6)
Пропускная способность оптического коммутатора. Так как во всех состояниях системы, кроме 
, поступающие пакеты обрабатываются коммутатором, т. е. либо сразу передаются на обслуживающее устройство, как это происходит в состоянии
, либо задерживаются в буфере, в случае нахождения коммутатора в одном из k-х состояний (
), а сумма вероятностей всех состояний равна единице, то пропускная способность оптического коммутатора в переходном режиме определяется как 
, где 
– интенсивность поступления пакетов. Окончательное выражение для пропускной способности оптического коммутатора в переходном режиме,
с учетом (6), имеет вид
Время переходного режима. Время переходного режима – это время с момента начала переходного режима до перехода его в установившееся состояние, т. е. состояние, когда его характеристики можно будет считать постоянными и не зависящими от времени. Для определения времени переходного режима для начала необходимо определить постоянную времени по формуле
(7)
где α – действительная часть комплексной переменной s.
Выражение (7) означает, что из всех нулей полинома 
необходимо выбрать ненулевой корень уравнения = 0, где
с наименьшей действительной частью ai, 
– мнимая часть. Наименьшее ai определит наибольшее значение постоянной времени [13].
Зная постоянную времени, можно определить время переходного режима по формуле 
.
Анализ переходного режима оптического коммутатора на примере системы M/M/1/2
Рассмотрим численный расчет характеристик производительности оптического коммутатора на примере системы M/M/1/2 с размером буфера, равным 2, и общим числом состояний, равным 4. Следует отметить, что выбранный размер буфера определяется особенностями построения оптических линий задержки, не предназначенных для хранения большого объема информации. Система уравнений Колмогорова, описывающая работу данной системы, имеет вид
(8)
Алгоритм нахождения вероятностей состояний оптического коммутатора.
Найдем определитель матрицы коэффициентов системы (8):
1. Определим корни характеристического уравнения четвертого порядка матрицы , которое имеет вид
(9)
Из анализа уравнения (9) следует, что один из корней равен нулю, а для нахождения оставшихся трех необходимо решить уравнение
(10)
Корни уравнения (10) находятся с использованием метода Кардано.
2. Определим многочлены , где 
:
где P0(0), P1(0), P2(0), P3(0) – вероятности состояний системы в начальный момент времени (начальные условия).
3. Перейдем от изображений к оригиналу с использованием формулы (5).
Для получения численных значений рассмотрим оптическую сеть с пропускной способностью, равной 1 Гбит/с, и длиной пакета 1 500 байт. Тогда интенсивность поступления пакетов λ, соответствующая данным параметрам сети, равна 89 479 пакетов/c. Проанализируем временную зависимость вероятностей состояний системы, пропускную способность и время переходного режима для случаев r > 1, r = 1, r < 1, где r = λ / μ – загрузка системы.
Рассмотрим первый случай, когда λ < μ,
λ = 89 479 пакетов/c, μ = 134 218,5 пакетов/c, т. е.
r = 0,67. Начальные условия, означающие, что буфер системы полностью свободен в момент t = 0, определим следующим образом:
(P0(0), P1(0), P2(0), P3(0)) = (1, 0, 0, 0).
На рис. 2 представлена зависимость вероятностей состояний от времени для данного случая.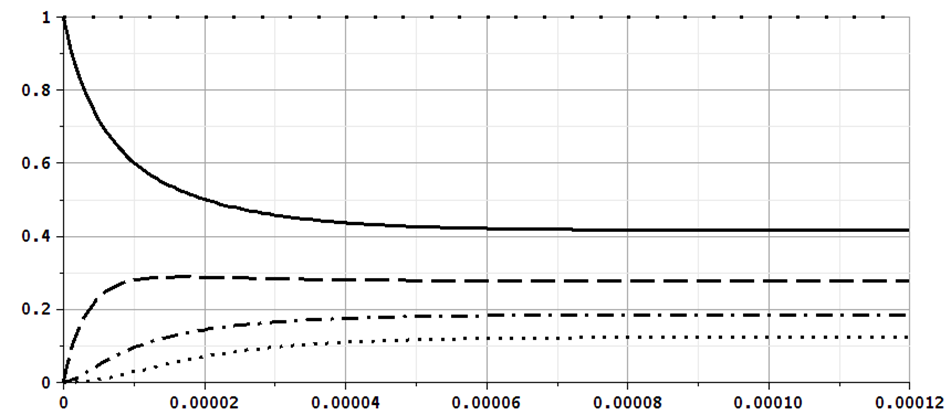
Рис. 2. Зависимость вероятностей состояний системы M/M/1/2 от времени, λ < μ
Fig. 2. Dependence of the probabilities of states of the system M/M/1/2 on time, λ < μ
Так как gmin = 68 715, то постоянная времени
tmin » 1,46 × 10–5 c, а время переходного режима
tпер » 7,3 × 10–5 c.
Следует отметить, что в стационарном режиме вероятности состояний равны следующим значениям: p0 = 0,42; p1 = 0,28; p2 = 0,19; p3 = 0,12, что подтверждает результаты, полученные по известной формуле 
[1, 2, 13].
Рассмотрим второй случай, когда λ = μ = 89 479 пакетов/c, т. е. r = 1 (рис. 3).
|
|
Рис. 3. Зависимость вероятностей состояний системы M/M/1/2 от времени, λ = μ
Fig. 3. Dependence of the probabilities of states of the system M/M/1/2 on time, λ = μ
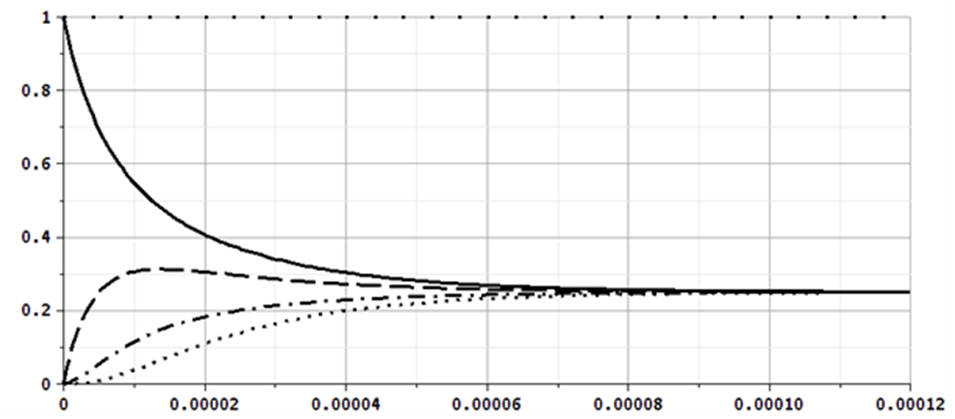
Для данного случая αmin = 52 417, постоянная времени tmin » 1,9 × 10–5 c, время переходного режима tпер » 9,5 × 10–5 c. В стационарном режиме вероятности состояний равны p0 = p1 = p2 = p3 = 0,25, что также совпадает с известными результатами [1, 2, 13].
Рассмотрим третий случай, когда λ > μ, r > 1,
λ = 89 479 пакетов/c, μ = 49 479 пакетов/c, т. е.
r = 1,81 (рис. 4).
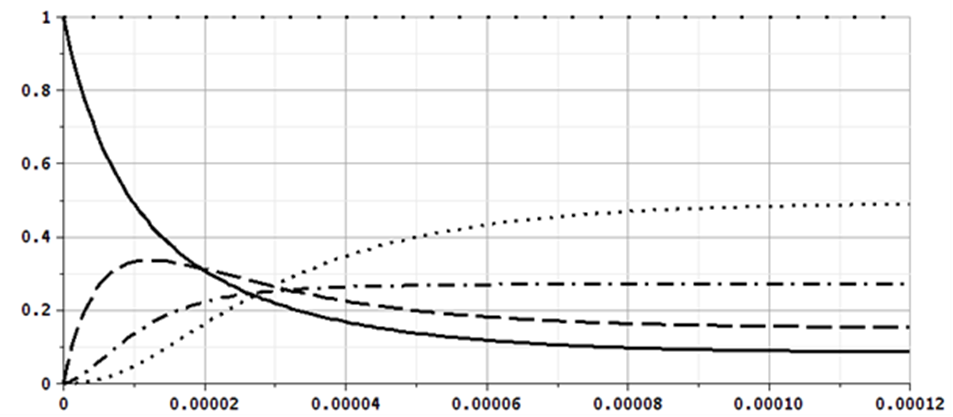
Рис. 4. Зависимость вероятностей состояний системы M/M/1/2 от времени, λ > μ
Fig. 4. Dependence of the probabilities of states of the system M/M/1/2 on time, λ > μ
В стационарном режиме вероятности состояний равны p0 = 0,08; p1 = 0,15; p2 = 0,27; p3 = 0,49, они совпадают со значениями, вычисленными по формуле [1, 2, 13], что подтверждает корректность полученных результатов.
Согласно расчетам gmin = 44 859, постоянная времени tmin » 2,2 × 10–5 c, а время переходного режима tпер » 1,1 × 10–4 c. Таким образом, при уменьшении интенсивности обслуживания оптического коммутатора μ время переходного режима увеличивается.
Исследуем зависимости пропускной способности оптического коммутатора A(t) в переходном режиме для трех вышеописанных случаев. На рис. 5 A1(t) – пропускная способность оптического коммутатора для случая r < 1; A2(t) – пропускная способность оптического коммутатора для случая r = 1; A3(t) – пропускная способность оптического коммутатора для случая r > 1.
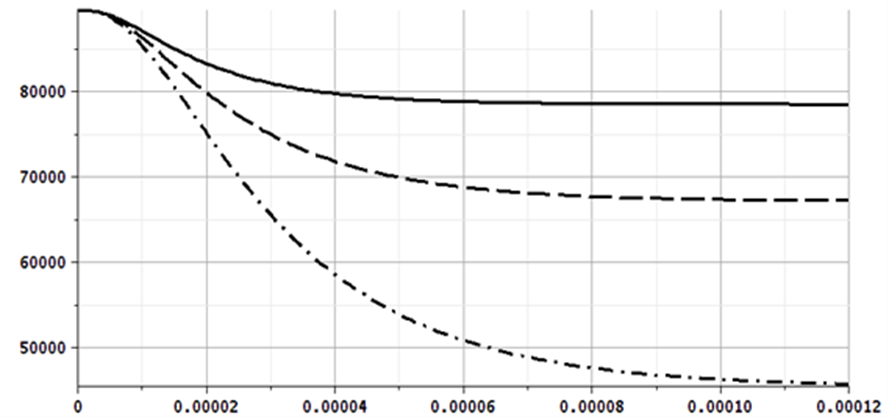
Рис. 5. Зависимость пропускной способности системы M/M/1/2 от времени при разных r
Fig. 5. Dependence of throughput capacity of the system M/M/1/2 on time at different r
В стационарном режиме пропускная способность оптического коммутатора для случая r < 1
и r > 1 вычисляется по формуле
= (1–
)l,
где ploss – вероятность потерь в стационарном режиме [13]. Для случая r = 1 пропускная способность 
= (
)l [13]. Таким образом, пропускная способность оптического коммутатора в стационарном режиме, пакетов/c, для трех случаев:
A1 = (1– 
) × 89 479 = 78 357;
A2 = (1 – 0,25) × 89 479 = 67 109;
A3 = (1–
) × 89 479 = 45 322.
Анализ зависимостей, представленных на
рис. 5, показывает, насколько уменьшается пропускная способность оптического коммутатора при переходе в стационарный режим при различной загрузке сети: чем больше загрузка системы r, тем больше разница между значением пропускной способности в начальный момент времени и ее значением в стационарном режиме.
Заключение
В данной работе проведен анализ переходного режима работы оптического коммутатора, представленного в виде модели однолинейной системы массового обслуживания с ограниченным буфером, пуассоновским входным потоком и экспоненциальным распределением времени обслуживания. Для решения уравнений Колмогорова и нахождения вероятностей состояний системы в переходном режиме использован аппарат преобразования Лапласа. В численном примере рассмотрена модель коммутатора с буфером, рассчитанным на хранение двух пакетов, и характеристиками реальной оптической сети. Рассмотрены случаи как нормального функционирования сети, так и ее перегрузки.
Предложенная аналитическая модель позволяет исследовать переходные характеристики производительности коммутатора оптической сети, такие как пропускная способность, вероятность потерь, время переходного режима, и может быть использована при проектировании оптических коммутационных устройств с заданными характеристиками производительности.
1. Вишневский В. М., Дудин А. Н. Системы массового обслуживания с коррелированными входными потоками и их применение для моделирования телекоммуникационных сетей // Автоматика и телемеханика. 2017. № 8. С. 3-59.
2. Barabanova E., Vytovtov K., Vishnevsky V., Kha-fizov I. Analysis of Functioning Photonic Switches in Next-Generation Networks Using Queueing Theory and Simulation Modeling // Communications in Computer and Information Science. 2023. V. 1748. P. 356-369.
3. Горцев А. М., Бочарова М. А. Аналитическое исследование однолинейной системы массового обслуживания с входящим синхронным потоком событий // Вестн. Томск. гос. ун-та. Управление, вычислительная техника и информатика. 2022. № 59. С. 34-46. DOI:https://doi.org/10.17223/19988605/59/4.
4. Клименок В. И. Многолинейная система массового обслуживания с резервными приборами // Журн. Белорус. гос. ун-та. Математика. Информатика. 2019. № 3. C. 57-70.
5. Бондрова О. В., Жук Т. А., Головко Н. И. Анализ уравнений со скачкообразной интенсивностью входного потока // Математ. заметки СВФУ. 2018. Т. 25, № 3. С. 18-32. DOI:https://doi.org/10.25587/SVFU.2018.99.16948.
6. Копать Д. Я., Маталыцкий М. А. Анализ в не-стационарном режиме экспоненциальной G-сети с обходами систем обслуживания положительными заявками // Вестн. Томск. гос. ун-та. Управление, вычислительная техника и информатика. 2020. № 52. С. 66-72. DOI:https://doi.org/10.17223/19988605/52/8.
7. Маталыцкий М. А., Копать Д. Я. Анализ в переходном режиме сети с нетерпеливыми положительными и отрицательными заявками различных типов // Вестн. Томс. гос. ун-та. Управление, вычислительная техника и информатика. 2018. № 42. С. 60-71. DOI:https://doi.org/10.17223/19988605/42/7.
8. Shyam S. S., Ram P. G. Transient analysis of queueing model // Journal of the Institute of Engineering. 2015. V. 11 (1). P. 165-171. DOI:https://doi.org/10.3126/jie.v11i1.14711.
9. Rakesh K., Bhavneet S. S. Transient numerical analysis of a queueing model with correlated reneging, balking and feedback // Reliability: Theory & Applications. 2019. N. 4 (55). P. 46-54.
10. Kaczynski W. H., Leemis L. M., Drew J. H. Tran-sient queueing analysis // INFORMS Journal on Computing. 2012. V. 24, no. 1. P. 10-28.
11. Барабанова Е. А., Вытовтов К. А., Барабанов И. О., Мальцева Н. С. Модель и алгоритм работы оптического коммутатора 4 × 4 // Вестн. Астрахан. гос. техн. ун-та. Сер.: Управление, вычислительная техника и информатика. 2019. № 2. С. 48-55. DOI:https://doi.org/10.24143/2072-9502-2019-2-48-55.
12. Лунц Г. Л., Эльсгольц Л. Э. Функции комплексного переменного (с элементами операционного исчисления). М.: Лань, 2002. 292 с.
13. Барабанова Е. А., Вытовтов К. А. Аналитический метод исследования поведения системы массового обслуживания при скачкообразно-изменяющихся потоках информации // Физические основы приборостроения. 2021. № 1. С. 36-47. DOI:https://doi.org/10.25210/jfop 2101-036047.
