Россия
Россия
Россия
Рассматривается возникающая при решении транспортных технических проблем задача разбиения транспортной сети взаимосвязанных терминалов на фиксированное число относительно автономных транспортных узлов. Предложен распространенный и достаточно простой вариант задач разрезания графа – задача сегментации транспортной сети путем r-разрезания. Изучаются полезные с практической точки зрения процедуры решения данной задачи. Предложен вариант оценки развития упомянутых процедур сегментации транспортной сети, их содержательности. Сформулирована эвристическая процедура сегментации транспортной сети по свойству отделимости для формирования систем транспортных узлов. Для рассматриваемых эвристических процедур решения поставленной задачи проводится изучение их свойств, строятся оценки наихудшего поведения. Определено, что сегментация транспортной сети региона на отдельные транспортные узлы по описанным процедурам может быть осуществлена для подкласса отделимых или отделимых в среднем разбиений, если будет реализовываться оценка, которую в принципе уже нельзя улучшить. Рассмотренные процедуры сегментации графа транспортной сети региона связаны одной общей чертой. Эти процедуры обеспечивают сохранение некоторых полезных свойств разбиениями, получаемыми в ходе формирования транспортного узла. Отмечено, что процедуры могут служить обоснованием при синтезе иерархической группировки, представленной в виде цепочки вложенных разбиений, каждое из которых является «хорошим» в смысле требований кластерного анализ. Содержательность оценок разбиений транспортной сети на транспортные узлы анализируется с помощью вычислительного эксперимента.
транспортный узел, разбиение транспортной сети, транспортная сеть, сегментация транспортной сети, терминал
Введение
При решении технических проблем, связанных с проектированием и анализом деятельности транспортных сетей и транспортных узлов, может возникнуть задача оптимального разбиения транспортной сети того или иного региона на множество взаимосвязанных систем транспортных узлов, которые в свою очередь являются относительно автономными подмножествами терминалов. В математической постановке эта задача может быть сведена к известной задаче разрезания сети (графа) [1–3]. На практике для решения обозначенной задачи обычно используются эвристические методы разбиения, что объясняется значительной сложностью и трудоемкостью точных алгоритмов разбиения. В связи с этим актуальной является проблема изучения свойств различных эвристических процедур разбиения и оценки их эффективности [3]. В данном случае рассматривается распространенный и достаточно простой вариант задач разрезания графа – задача r-разрезания – и изучаются полезные с практической точки зрения процедуры решения данной задачи. Кроме того, в статье предложен вариант оценки наихудшего развития упомянутых процедур сегментации транспортной сети, их содержательности [4, 5].
Постановка задачи
Пусть задана транспортная сеть какого-либо региона, модель которой представлена в виде взвешенного графа G с множеством вершин (терминалов) N = {l, 2, ..., n}. Каждое разбиение – транспортный узел р – может состоять из взаимно непересекающихся множеств терминалов N1, N2, ... , Nr(p), каждый из которых будем характеризовать величиной внутреннего веса IW, заданного как
![]()
где ωik – вес ребра (i, k) в графе G, равный грузообороту между терминалами i и k, причем если ребро графа (i, k) отсутствует, то следует принимать ωik = 0.
В данном варианте сегментации транспортной сети требуется найти разбиение множества вершин графа сети N на r непустых подмножеств (узлов), имеющих наибольшее значение внутреннего веса. Для этой цели введем ряд дополнительных обозначений. Пусть:
– суммарный вес ребер графа
![]()
– внешний вес разбиения
![]()
– суммарный вес ребер подмножества вида
![]()
если
![]()
где вес связей подмножеств K и M Ì N;
– средний вес ребер множества
![]()
Если множество М состоит только из одной вершины (|M| = 1), то необходимо принимать величину q(M) = ∞, а средний вес связей между множествами Nj и Nl определять через значение
ljl (p) = W(Nj, Nl) / njnl.
Здесь и далее ns = |Ns| – мощность множества Ns, причем число внутренних связей в разбиении p определяется как
![]()
а число внешних связей в разбиении p определяется следующим образом:
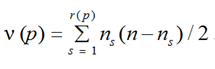 .
.
Используя введенные обозначения, опишем первый вариант эвристической процедуры решения задачи по формированию в транспортной сети региона систем транспортных узлов (процедура П1). Для этой цели будем считать, что число п кратно числу r, или n = rh. В противном случае множество N можно дополнить необходимым числом изолированных вершин. Затем произвольным образом построим исходное разбиение множества N на r подмножеств по h элементов (терминалов) и на каждом последующем шаге (итерации) некоторым образом будем выбирать пары вершин графа из различных подмножеств I Î Ns, j Î Nt, причем такие, чтоб
![]() (1)
(1)
Далее в процедуре будем производить обмен, при котором вершина i включается в множество Nt, а вершина j – в множество Ns, который увеличивает внутренний вес разбиения. Если пары вершин, удовлетворяющей выражению (1), не существует, то эвристическая процедура сегментации вершин графа прекращается.
В качестве второй процедуры (процедуры П2) формирования в транспортной сети региона систем транспортных узлов можно рассмотреть такую схему сегментации, при которой на нулевом шаге множество N рассматривается как набор из одноэлементных подмножеств, а на каждом последующем шаге по определенному правилу выбирается пара подмножеств Ns и Nt и производится их объединение. На шаге (n – r) получаем искомое разбиение вершин графа на r подмножеств.
Очевидно, что как в первой, так и второй процедуре для полного описания конкретного процесса сегментации достаточно указать только используемое правило выбора или правило выбора и метод дихотомии соответственно.
Условия отделимости структуры транспортного узла от транспортной сети региона
Для описания процедуры сегментации допустим, что IА – значение внутреннего веса разбиения, полученного с помощью одной из вышеописанных процедур сегментации транспортной сети региона П, а величина I* – оптимальное значение внутреннего веса полученных разбиений. В описанных выше эвристических процедурах или их конкретизациях можно найти нижние оценки вида IП Î cSW, где с < 1, при этом очевидно, что 1П > сI*.
Полученные оценки обусловлены свойствами кластерного анализа. С учетом этих свойств можно сформулировать предположение о правиле отделимости для множества терминалов транспортной сети, обладающего свойством транспортного узла [6, 7]. Так, разбиение терминалов р = (N1, N2, ..., Nr) будет являться отделимым от транспортной сети региона, если существует неотрицательное число α (порог отделимости), причем такое, чтоб
![]()
для любых i, s, t = 1, r.
Отделимое разбиение терминалов транспортного узла компактно в смысле [1], а каждый терминал из подмножеств транспортного узла можно назвать сгущением в среднем [1].
Введем еще один ослабленный вариант свойства отделимости разбиения терминалов от транспортной сети. Так, разбиение р = (N1, N2, ..., Nr) можно называть отделимым в среднем, если выполняется условие, записанное как
![]() (2)
(2)
то есть средний вес внутренних связей терминалов больше среднего веса внешних связей этих же терминалов. Величину, равную
![]()
можно принять в качестве порога отделимости разбиения в среднем, причем это свойство эквивалентно некоторой нижней оценке для величины IW(p).
Разбиение терминалов р будет отделимо в среднем только тогда, когда выполняется условие вида
![]() (3)
(3)
Это утверждение достаточно просто подтвердить. Если записать неравенство (2) в виде
![]()
то, подставляя выражение
![]()
и учитывая, что
![]()
получим отношение
![]()
которое является эквивалентным выражению (3).
Здесь следует заметить, что все применяемые преобразования являются тождественными, и поэтому из выражения (3) всегда можно получить отношение (2). Кроме того, оценка (3) достижима как в классе отделимых в среднем для разбиений, так и в более узком подклассе отделимых разбиений. Любое разбиение р полного графа транспортных сетей региона с единичными весами ребер отделимо с порогом, равным α = 1, при этом выполняется равенство
![]()
Таким образом, сегментация транспортной сети региона на отдельные транспортные узлы по вышеописанным процедурам может быть осуществлена для подкласса отделимых или отделимых в среднем разбиений, если будет реализовываться оценка вида (3), которую в принципе уже нельзя улучшить.
Оценка отделимости транспортного узла от транспортной сети региона
Для процедуры сегментации графа транспортной сети П1 разбиение, получаемое по окончании действий этой процедуры, отделимо в среднем. Очевидность этого заключения следует из свойства различимости подмножеств I Î Ns, j Î Nt при выполнении неравенства
![]()
Тогда, суммируя эти неравенства, можно получить условие для реализации процесса сегментации транспортной сети на отдельные транспортные узлы вида (1).
Заметим, что разбиения, получаемые по окончании работы процедуры П1, отделимы от транспортной сети региона в среднем, и для них будет иметь место оценка (3). Кроме того, нетрудно показать, что
![]()
где h = [n / r].
Поэтому для отделимого в среднем разбиения имеет место неравенство
![]()
Отсюда следует
![]() (4)
(4)
Оценка (4) достигается в произвольной процедуре П1 при решении задачи разрезания полного графа Kп с единичными весами ребер с правилом выбора: для обмена выбирается пара вершин, максимизирующая разность левой и правой частей неравенства (1).
Перейдем к оценке свойств разбиений транспортной сети, получаемых в ходе использования эвристической процедуры П2. Процедурой П2 будем называть любой вариант сегментации графа транспортной цепи, в котором выбор пары подмножеств Ns и Nt на каждом шаге сегментации производится с соблюдением условия вида [8–10]
![]() (5)
(5)
При этом любая конкретная процедура П2 будет порождать на каждом шаге сегментирования графа транспортной сети отделимое разбиение.
Заметим, что для соблюдения условия (5) на нулевом шаге следует объединить пару вершин, связанных ребром максимального веса. На очередном k-м шаге возможность выбора пары подмножеств, удовлетворяющих условию (5), получается из отделимости полученного на предыдущем шаге разбиения рk. Пусть
![]()
С учетом отделимости ph имеем
![]()
а уже с учетом этих неравенств получим
![]()
то eсть
![]()
Другим интересным вариантом процедуры П2 является процедура типа П2*, в которой при выборе пары Ns и Nt на каждом шаге процедуры соблюдается условие
![]() (6)
(6)
Тогда процедура сегментации графа транспортной сети П2* порождает на каждом шаге отделимое в среднем разбиение терминалов.
При решении практической задачи сегментации графа транспортной сети можно рекомендовать процедуру П2 со следующими правилами выбора:
![]() (7)
(7)
![]()
При сегментации графа транспортной сети Kn с единичными весами ребер в рамках процедур П2 и П2* можно использовать оценку (4). При этом легко видеть, что правило выбора (7) обеспечивает выполнение условий (5) и (6) одновременно, поэтому оценка (4) не является улучшаемой как в процедуре П2, так и в процедуре П2*.
Итак, рассмотренные выше процедуры П1, П2 и П2* сегментации графа транспортной сети региона связаны одной общей чертой. Эти процедуры обеспечивают сохранение некоторых полезных свойств разбиениями, получаемыми в ходе формирования транспортного узла. Кроме того, процедуры могут служить обоснованием при синтезе иерархической группировки, представленной в виде цепочки вложенных разбиений, каждое из которых является «хорошим» в смысле требований кластерного анализа [3].
Обсуждение полученного результата
С практической точки зрения оценка IП > сSW тем положительней и содержательней, чем меньше ее относительная погрешность вида
![]() ,
,
усредненная по всему множеству процедур возможных сегментаций графа транспортной сети.
С целью анализа поведения усредненной относительной погрешности оценки <εП> в зависимости от числа подмножеств r и разброса элементов
в матрице W = ||ωik||. Вычислительный эксперимент проводился по процедуре П2 с правилом выбора (7) и по процедуре П1. В качестве элементов матрицы W выбирались случайные числа, равномерно распределенные на некотором целочисленном отрезке [А, В], причем разброс измерялся коэффициентом, равным величине
![]() .
.
Для каждого конкретного значения числа подмножеств r и коэффициента разброса k счет проводился на 40 случайно сгенерированных матрицах размером 48 × 48. Результаты счета приведены в табл. 1 и 2. На основании полученных результатов можно сделать выводы. Для малого числа подмножеств (r = 4) и небольшого коэффициента разброса (k = 1/3 и 2/3) погрешность оценки невелика, кроме того, погрешность оценки для процедуры П1 существенно меньше погрешности для процедуры П2. Погрешность оценки возрастает, если увеличивается коэффициент разброса и если увеличивается число транспортных узлов.
Таблица 1
Table 1
Относительная погрешность оценки отделимости транспортного узла от транспортной сети региона
по процедуре П2 <εП2>
Relative error of assessment of the transport junction separability from the regional transport network
by the procedure П2 <εП2>
|
k |
r |
|||
|
4 |
6 |
8 |
12 |
|
|
1 |
0,53 |
0,64 |
0,73 |
0,91 |
|
2/3 |
0,41 |
0,48 |
0,41 |
0,55 |
|
2/5 |
0,11 |
0,17 |
0,22 |
0,36 |
Таблица 2
Table 2
Относительная погрешность оценки отделимости транспортного узла от транспортной сети региона
по процедуре П1 <εП1>
Relative error of assessment of the transport junction separability from the regional transport network
by the procedure П1 <εП1>
|
k |
r |
|||
|
4 |
6 |
8 |
12 |
|
|
1 |
0,31 |
0,47 |
0,52 |
0,65 |
|
2/3 |
0,17 |
0,23 |
0,25 |
0,31 |
|
1/3 |
0,07 |
0,09 |
0,10 |
0,12 |
|
– |
– |
– |
– |
– |
Для процедуры П1 рост погрешности выражен более четко, однако во всех приведенных случаях он не превышает единицы.
Заключение
Предложенные эвристические процедуры сегментации графа транспортной сети региона обеспечивают, во-первых, сохранение некоторых полезных свойств всеми разбиениями, получаемыми в ходе формирования транспортного узла. Кроме того, эти процедуры могут служить обоснованием для составления иерархической группировки, составленной из цепочки вложенных разбиений, каждое из которых является «хорошим» в смысле требований кластерного анализа. Процесс сегментации транспортной сети региона на отдельные транспортные узлы по предложенным эвристическим процедурам может быть осуществлен для подкласса отделимых или отделимых в среднем разбиений, причем этот процесс будет реализовываться, если привлекать оценку отделимости, которую в принципе уже нельзя улучшить.
Рассмотренные выше процедуры сегментации графа транспортной сети региона связаны одной общей чертой. Эти процедуры обеспечивают сохранение некоторых полезных свойств разбиениями, получаемыми в ходе формирования транспортного узла. Кроме того, процедуры могут служить обоснованием при синтезе иерархической группировки, представленной в виде цепочки вложенных разбиений, каждое из которых является «хорошим» в смысле требований кластерного анализа.
1. Мелихов А. Н., Берштейн Л. С., Курейчик В. М. Применение графов для проектирования дискретных устройств. М.: Наука, 1974. 303 с.
2. Купершох В. Л., Миркин Б. Г., Трофимов В. А. Сумма внутренних связей как показатель качества классификации // Автоматика и телемеханика. 1976. № 3. С. 133-141.
3. Дюран Б., Одел П. Кластерный анализ / пер. с англ. Е. З. Демиденко. М.: Статистика, 1977. 127 с.
4. Гермейер Ю. Б., Ватель И. А. Игры с иерархическим вектором интересов // Техническая кибернетика. 1974. № 3. С. 54-69.
5. Нейман Д., Моргенштерн О. Теория игр и экономическое поведение / пер. с англ. Н. Н. Воробьева. М.: Наука, 1970. 707 с.
6. Эглит Я. Я., Эглите К. Я., Артемьев А. В. Транспортные системы доставки грузов. СПб.: Феникс, 2005. 300 с.
7. Эглит Я. Я., Эглите К. Я., Прокофьев В. А. Управление транспортными системами. СПб.: Изд-во Акад. трансп. России, 2004. 423 с.
8. Браверман Э. М., Левин М. И. Идентификация эффективных состояний сетей производственных элементов. I // Автоматика и телемеханика. 1978. № 6. С. 67-82.
9. Браверман Э. М., Левин М. И. Идентификация эффективных состояний сетей производственных элементов. II // Автоматика и телемеханика. 1978. № 7. С. 79-86.
10. Браверман Э. М. Модель потребительского выбора при фиксированных ценах // Автоматика и телемеханика. 1976. № 5. С. 100-111.

















