Пенза, Пензенская область, Россия
Предложен метод ускоренной оценки энтропии Шеннона для двоичных последовательностей, в том числе генерируемых нейросетевым преобразователем «биометрия – код». Ключевая идея заключается в установ-лении функциональной связи между коэффициентом корреляции Пирсона отдельных разрядов и энтропией 256-разрядного кода, что исключает необходимость полного перебора всех битовых конфигураций. На начальном этапе формируется массив псевдослучайных последовательностей длиной до 256 бит, каждая из которых разбивается на блоки фиксированной длины. Для каждого блока вычисляются вероятности появления всех возможных комбинаций и соответствующие им значения энтропии, после чего путем агрегирования с учетом межблочных корреляций определяется итоговая энтропия всей последовательности. Полученные пары «коэффициент корреляции – энтропия» формируют таблицу в диапазоне корреляций от 0 до 1 с шагом 0,1 либо 0,01 в зависимости от выбранного параметра шага перед началом синтеза таблицы. Далее указанная табличная зависимость аппроксимируется полиномиальной функцией, что снижает вычислительную сложность задачи с экспоненциальной до полиномиальной. Результаты численного моделирования демонстрируют, что аппроксимационная погрешность не превышает точности прямого метода Шеннона при сокращении временных затрат. Синтезированная таблица основывается исключительно на статистических характеристиках последовательности, что обеспечивает возможность универсального применения для кодов, сформированных различными биометрическими преобразователями. Представленный подход целесообразно интегрировать в доверенные микроконтроллеры низкой разрядности и иные устройства с ограниченными ресурсами, а также в российские операционные системы повышенной безопасности (например, Astra Linux) для оперативной и надежной оценки случайности выходной последовательности нейросетевого преобразователя «биометрия – код».
биометрия, преобразователь «биометрия – код», энтропия, коэффициент корреляции, полиномиальная аппроксимация, доверенная среда
Введение
История биометрических технологий уходит корнями в древние цивилизации. Например, в древнем Китае отпечатки пальцев использовались для подписания документов еще в 200 г. до н. э. В XIX в. сэр Фрэнсис Гальтон заложил основы современной биометрии, изучая уникальность отпечатков пальцев. В XX в. развитие вычислительной техники и алгоритмов машинного обучения привело к появлению современных систем, таких как распознавание лиц и голоса. Сегодня биометрия активно применяется в мобильных устройствах, системах контроля доступа и банковских приложениях, что подчеркивает необходимость эффективных методов оценки качества генерируемых биометрических кодов [1]. Биометрическая аутентификация, основанная на физиологических или поведенческих характеристиках пользователя, является перспективной альтернативой традиционным паролям и PIN-кодам [1–3]. Такой метод реализуется с помощью преобразователя «биометрия – код», генерирующего уникальный 256-разрядный код на основе биометрических шаблонов (отпечатка пальца, рисунка вен ладони, голоса и др.) [1, 2]. Биометрические данные всегда при пользователе, поэтому нет необходимости запоминать пароли, а прямой перебор биометрического кода занимает десятки лет [3]. В ходе обучения нейросетевого преобразователя «биометрия – код» контроль качества выходной последовательности выполняется при каждой итерации обучения. Показателем такой проверки служит энтропия Шеннона – количественная мера случайности двоичного кода [4]. Чем ближе ее значение к теоретическому максимуму, равному длине последовательности, тем меньше вероятность ложного допуска «Чужого» и необоснованного отказа «Своему» пользователю [5, 6]. Однако классический метод вычисления энтропии по формуле Шеннона [4, 7] предполагает экспоненциальный перебор всех возможных состояний, что делает его непригодным для устройств с малым потреблением [7, 8]. Например, согласно ГОСТ Р ИСО/МЭК 19795-1-2007, объем тестовых данных N растет экспоненциально с увеличением разрядности кода i:
Существуют альтернативные методы, такие как статистика расстояний Хэмминга h [9], позволяющие ускорить расчет энтропии за счет побитовых сравнений:
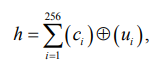
где c𝑖 – состояние i-го разряда последовательности «Свой»; ui – состояние i-го разряда последовательности «Чужой»; ⊕ – операция сложения по модулю два [10, 11].
Однако метод Хэмминга не учитывает многомерные корреляционные зависимости между разрядами кодов. Корреляция битов приводит к значительному снижению фактической энтропии, что наглядно иллюстрирует исследование радужной оболочки глаза, где вместо максимально возможных 2 048 независимых бит реально используется только около 245 бит из-за локальных корреляций [12, 13]. Несмотря на это, даже оставшегося объема (~245 бит) достаточно для обеспечения уникальности. К тому же, если два случайных бита кодовой последовательности не коррелированы, их совместная энтропия равна сумме индивидуальных энтропий. Для реализации быстрой проверки «случайности» кода на этапах обучения сети разработан облегченный, но статистически строгий алгоритм. Сначала формируется табличная зависимость между энтропией Шеннона и абсолютным коэффициентом корреляции Пирсона для 256-разрядных последовательностей. Затем эта дискретная связь аппроксимируется полиномом, а полученная программная реализация встраивается непосредственно в прошивку микроконтроллеров с малым энергопотреблением. Такой прием понижает вычислительную сложность оценки энтропии с экспоненциальной до полиномиальной и обеспечивает надежный контроль качества выходного кода даже на ресурсно-ограниченных платформах [8].
Методика синтеза таблицы связи
Методика исследования состояла в разработке программного обеспечения, реализованного на языке программирования C++ с использованием библиотеки Qt [14] для организации графического интерфейса и библиотеки Boost [15] для работы с большими числами, а также в тестировании полученных результатов. Разработка программного обеспечения осуществлялась на ноутбуке, оснащенном процессором Intel Core i5-12450HX, 24 ГБ оперативной памяти, твердотельным накопителем Micron MTFDKCD512QFM объемом 512 ГБ и работавшем под управлением операционной системы Windows 11, однако благодаря использованию кроссплатформенного фреймворка Qt [14] разработанное приложение может без каких-либо существенных изменений использоваться также на российской операционной системе Astra Linux. На первом этапе генерируется матрица псевдослучайных чисел, распределенных по нормальному закону со средним значением 0 и стандартным отклонением 1 [16], что обеспечивает «шумоподобный» характер сигналов, моделирующих выходные состояния преобразователя «биометрия – код». Для генерации псевдослучайных данных использовался алгоритм Mersenne Twister (MT19937) [15], встроенный в стандартную библиотеку C++. Далее формируется последовательность y по формуле
![]() (1)
(1)
где a – коэффициент корреляционной связи со значениями от 0,01 до 0,99;
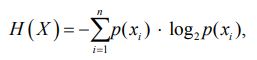 (2)
(2)
где H(X) – энтропия случайной величины X; xi – i-е возможное значение X; p(xi) – вероятность реализации значения xi; n – число возможных значений случайной величины X.
Результаты отображались в графическом интерфейсе приложения в виде журнала событий с указанием временных меток и текущих значений параметров. Для удобства работы была предусмотрена возможность сохранения итоговой таблицы значений энтропии и корреляции в CSV-файл [21] с указанием коэффициентов корреляции и соответствующих им значений энтропии. Процесс синтеза таблицы значений энтропии и корреляции представлен на рис. 1.
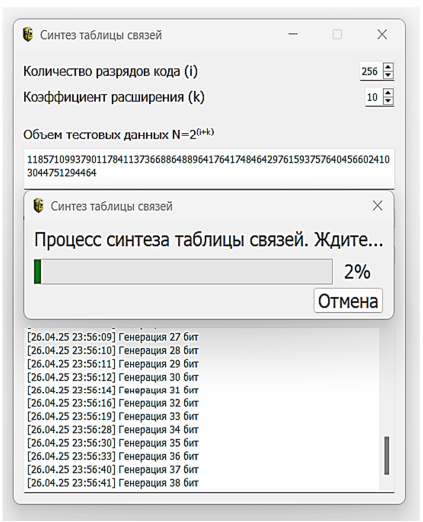
Рис. 1. Процесс синтеза таблицы значений энтропии и корреляции
Fig. 1. The process of synthesizing the table of entropy and correlation values
Применение разработанного подхода обеспечило повышение скорости синтеза таблицы, а также расширило возможности эксплуатации программного обеспечения на вычислительных системах с ограниченными ресурсами [8, 20]. Для оценки коэффициента корреляции использовалась формула Пирсона:
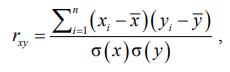 (3)
(3)
где 𝑥𝑖 и 𝑦𝑖 – элементы последовательности; n – размер последовательности; σ(x), σ(y) – выборочные среднеквадратические отклонения (стандартные отклонения) последовательностей x и y соответственно;
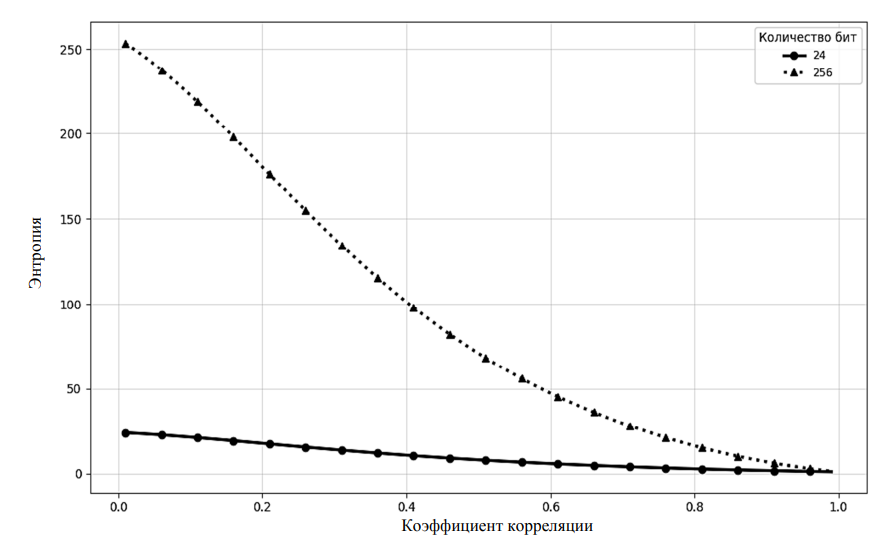
Рис. 2. Результат связи энтропии Шеннона со значениями корреляции Пирсона
Fig. 2. The result of the connection of Shannon entropy with the values of Pearson correlation
Анализ графика (см. рис. 2) показывает, что величина энтропии Шеннона является функцией коэффициента взаимной корреляции отдельных битовых разрядов: с ростом размерности кодовой последовательности растет динамический диапазон влияния коэффициента корреляционной связи [11, 16] на значение оцениваемой энтропии. Таким образом, с помощью программного обеспечения синтезирована таблица связи энтропии Шеннона и коэффициента корреляции Пирсона для бинарных кодов фиксированной разрядности [16, 21]. Таблица охватывает диапазон корреляций от 0 до 1 с шагом коэффициента корреляции Пирсона 0,1 или 0,01 (в зависимости от выбранного параметра перед началом синтеза таблицы) и содержит соответствующие значения энтропии [4, 21]. Пример фрагмента полученной синтезированной таблицы, содержащей значения энтропии Шеннона для различных коэффициентов корреляции Пирсона и кодов разрядностью от 2 до 256 бит, приведен в табл. 1.
Таблица 1
Table 1
Пример фрагмента синтезированной таблицы связи энтропии Шеннона
со значениями корреляции Пирсона
An example of a fragment of a synthesized table of the relationship between Shannon entropy
and Pearson correlation values
|
Количество бит |
Коэффициент корреляции Пирсона |
|||||||||
|
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,99 |
|
|
2 |
1,9832 |
1,9329 |
1,914 |
1,841 |
1,720 |
1,611 |
1,489 |
1,352 |
1,226 |
1,032 |
|
4 |
3,9565 |
3,7131 |
3,478 |
3,089 |
2,743 |
2,440 |
2,038 |
1,702 |
1,369 |
1,054 |
|
8 |
7,1253 |
5,9658 |
4,698 |
3,689 |
2,859 |
2,286 |
1,790 |
1,376 |
1,138 |
1,083 |
|
16 |
14,215 |
11,720 |
9,430 |
7,231 |
5,490 |
4,090 |
3,065 |
2,189 |
1,537 |
1,092 |
|
24 |
21,340 |
17,700 |
14,025 |
10,630 |
7,940 |
5,760 |
4,070 |
2,750 |
1,790 |
1,124 |
|
32 |
28,380 |
23,420 |
18,380 |
14,140 |
10,390 |
7,470 |
5,150 |
3,290 |
2,015 |
1,178 |
|
64 |
55,600 |
45,320 |
34,850 |
25,430 |
18,120 |
12,180 |
7,900 |
4,570 |
2,385 |
1,189 |
|
128 |
111,100 |
90,700 |
69,500 |
50,980 |
35,690 |
24,030 |
15,250 |
8,610 |
3,910 |
1,212 |
|
256 |
222,400 |
180,950 |
138,750 |
101,450 |
70,750 |
47,800 |
29,500 |
16,160 |
6,860 |
1,359 |
Сравнение времени расчета энтропии различными методами
После синтеза таблицы на основе выявленной зависимости между коэффициентом корреляции Пирсона и значением энтропии Шеннона построен полином 15-й степени с помощью метода polyfit библиотеки NumPy [22]. Для выбора оптимальной степени полинома проводилось систематическое тестирование вариантов от 1 до 20, с оценкой качества аппроксимации как на обучающей, так и на тестовой выборках (при этом контролировались критерии переобучения, в частности появление «волнообразных» осцилляций на участке аппроксимации). Начиная с 15-й степени кривая стала лучше описывать нелинейную зависимость, незначительно увеличивая вычислительные затраты. Дальнейшее увеличение степени приводило к росту времени вычислений. В результате 15-я степень полинома оказалась оптимальным компромиссом между точностью и быстродействием [13, 17]:
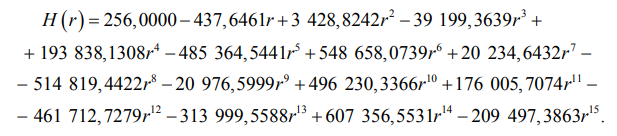
Численное моделирование подтвердило, что разработанная полиномиальная модель воспроизводит энтропию с пренебрежимо малыми систематической и среднеквадратической погрешностями. Для вновь сгенерированной 24-битной тестовой последовательности 𝑦 с заданным коэффициентом корреляционной связи a (формула (1)) вычислялась абсолютная ошибка ΔH – разность между эталонной энтропией Hsh, определяемой по классической формуле Шеннона (формула (2)), и ее аппроксимационным значением Hpoly, полученным по полиному с использованием автокорреляции данных, при этом оценка зависимости выполняется по коэффициенту корреляции Пирсона (формула (3)). Объем выборки составил 134 217 728 элементов и был ограничен доступным объемом оперативной памяти. Разрядность исследуемых последовательностей остановлена на уровне 24 бит, поскольку дальнейшее ее увеличение без пропорционального расширения выборки приводило к деградации статистической оценки и искажению результатов. Сводные значения ошибок приведены в табл. 2.
Таблица 2
Table 2
Сравнение прямого расчета энтропии и полиномиальной аппроксимации
Comparison of direct entropy calculation and polynomial approximation
|
а |
Hsh |
Hpoly |
ΔH = |Hsh − Hpoly| |
|
0,0 |
23,950 |
23,948 |
0,002 |
|
0,3 |
22,870 |
22,867 |
0,003 |
|
0,5 |
21,120 |
21,115 |
0,005 |
|
0,7 |
17,830 |
17,825 |
0,005 |
|
0,9 |
10,250 |
10,255 |
0,005 |
На рис. 3 иллюстрируется характер зависимости энтропии от коэффициента корреляции по данным, полученным методами Шеннона и полиномиальной аппроксимации.
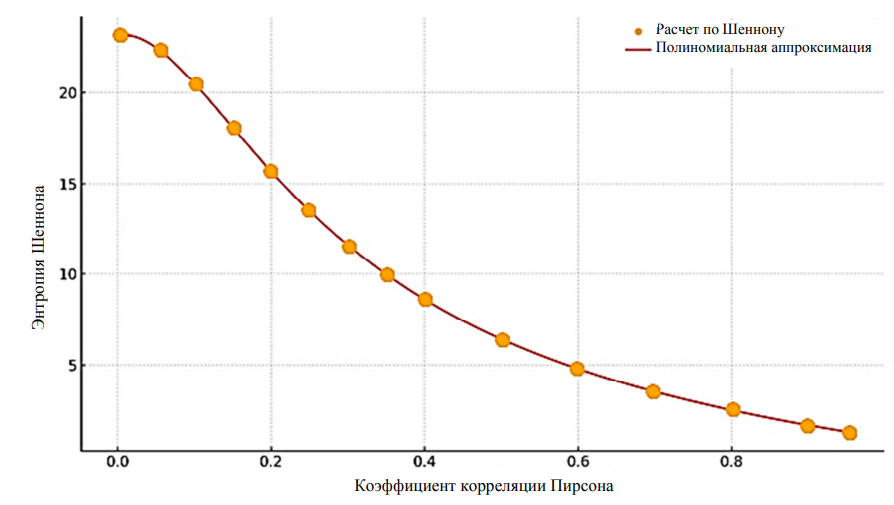
Рис. 3. Зависимости энтропии от коэффициента корреляции Пирсона для двоичного кода
Fig. 3. Dependence of entropy on the Pearson correlation coefficient for a binary code
По горизонтальной оси указано значение коэффициента корреляции Пирсона, по вертикальной – соответствующая ему энтропия Шеннона. Точки – результаты прямого расчета энтропии методом Шеннона, а кривая – результат полиномиальной аппроксимации 15-й степени. Аппроксимированные значения (см. рис. 3) практически полностью совпадают с точками прямого метода, подтверждая высокую точность предложенного подхода, а с ростом корреляции энтропия убывает нелинейно: при r < 0,1 она близка к максимуму (256 бит), тогда как при r > 0,8 стремится к минимальному уровню (≈ 1–2 бита). Одним из ключевых результатов работы является ускорение вычисления энтропии при использовании разработанного метода. На рис. 4 приведено сравнение времени выполнения операций для классического метода Шеннона и предложенной полиномиальной аппроксимации.
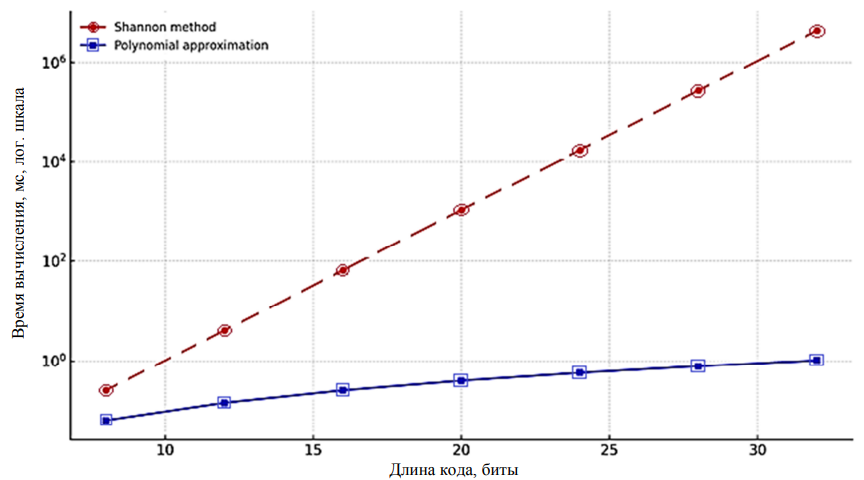
Рис. 4. Сравнение времени вычисления энтропии
Fig. 4. Comparison of entropy calculation time
Для наглядности время показано в логарифмической шкале. Хорошо заметно, что по мере увеличения разрядности двоичного кода время прямого расчета энтропии стремительно возрастает – график для метода Шеннона имеет экспоненциальный характер (см. рис. 4, прерывистая линия). Например, увеличение длины кода с 8 до 24 бит приводит к росту времени с долей миллисекунды до десятков секунд, а для 32 и более бит вычисление энтропии методом Шеннона уже измеряется минутами или часами. В случае 256-битного кода полный перебор всех комбинаций является вообще нереализуемым на практике [11, 13]. В то же время вычислительная сложность полиномиальной модели (см. рис. 4, сплошная линия) растет квадратично за счет вычисления корреляции, и даже для 256 бит это время остается в пределах миллисекунд. Таким образом, получение оценки энтропии методом полиномиальной аппроксимации фактически не зависит от длины кода и пригодно для применения в реальном времени. Получаемое при этом значение энтропии идентично результату классического метода Шеннона [4, 17], т. е. ускорение достигается без потери точности. Временные показатели приведены в миллисекундах (логарифмическая шкала по вертикали). Экспоненциальный рост времени для метода Шеннона делает его непригодным для кодов большой разрядности, тогда как полиномиальный метод обеспечивает близкое к постоянному времени вычисления даже для 256 бит. Для любой длины кода аппроксимация позволяет получить энтропию на несколько порядков быстрее, причем результаты обоих методов полностью совпадают [13]. Полученные результаты демонстрируют эффективность предложенного подхода. Применение заранее рассчитанной таблицы и полинома позволяет сократить вычислительную сложность оценки энтропии с экспоненциальной до полиномиальной [13, 17]. В эксперименте на моделируемых данных полиномиальная аппроксимация дала ускорение вычислений более чем в 106 раз по сравнению с прямым методом, в то время как расхождения в значениях энтропии отсутствовали (на уровне погрешности представления чисел с плавающей запятой). Это открывает возможность реализации оценки энтропии непосредственно в прошивку низкоразрядного микроконтроллера, что ранее считалось неосуществимым из-за ограничений по памяти и быстродействию [8]. Кроме того, предложенный метод универсален: однажды сформированная зависимость H(r) справедлива для различных типов биометрических данных, поскольку опирается лишь на статистические характеристики выходной последовательности, а не на детали конкретной биометрической технологии.
Заключение
В ходе исследования разработано приложение для синтеза и оценки качества 256-битных биометрических кодов. Синтезирована таблица связи энтропии Шеннона выходных кодов преобразователя «биометрия – код» с коэффициентами корреляции их разрядов, на основании которой реализована полиномиальная аппроксимация этой зависимости. Полученный подход позволяет вычислять энтропию длинного двоичного кода с меньшими вычислительными затратами по сравнению с классическим методом Шеннона. Численные эксперименты подтвердили, что энтропия, вычисленная по аппроксимированному полиному, практически полностью совпадает с энтропией, рассчитанной напрямую по формуле Шеннона, при этом время вычисления энтропии сокращается. Предложенный подход рекомендуется к внедрению в доверенные микроконтроллеры низкой разрядности, используемые в мобильных системах биометрической идентификации и аутентификации, в том числе в банковской сфере, системах контроля доступа и информационной безопасности. Метод особенно актуален в устройствах с ограниченными аппаратными ресурсами, таких как электронные пропуска, биометрические ключи и компактные устройства персональной идентификации. Также предложенный алгоритм можно интегрировать в российские операционные системы с повышенными требованиями к информационной безопасности, такие как Astra Linux, для обеспечения быстрой и надежной оценки стойкости биометрических кодов.
1. Постников Н. А. Биометрия сквозь века: от первых отпечатков к современным методам идентификации // Поволж. вестн. науки. 2025. № 1 (35). С. 31–41.
2. Psychology of Passwords. URL: https://www.lastpass.com/-/media/9fe0bf5dc473413b8ab4df3bd8688295.pdf (дата обращения: 20.10.2024).
3. Сколько времени потребуется для взлома вашего пароля // Hi-Tech Mail.Ru. 11.03.2022. URL: https://hi-tech.mail.ru/news/57214-skolko-vremeni-potrebuetsya-dlya-vzloma-vashego-parolya-posmotrite-tablicu/ (дата обращения: 20.10.2024).
4. Shannon C. E. A Mathematical Theory of Communication // Bell System Technical Journal. 1948. V. 27. N. 3. P. 379–423.
5. Jain A. K., Ross A., Prabhakar S. An Introduction to Biometric Recognition // IEEE Transactions on Circuits and Systems for Video Technology. 2004. V. 14. N. 1. P. 4–20.
6. Постников Н. А. Анализ методов и технологий биометрической идентификации // Новые информационные технологии и системы (НИТиС-2022): сб. науч. ст. по материалам XIX Междунар. науч.-техн. конф., посвящ. 75-летию каф. «Вычислительная техника» ПГУ (Пенза, 17–18 ноября 2022 г.). Пенза: Пенз. гос. ун-т, 2022. С. 140–143.
7. ГОСТ Р 52633.0-2006. Защита информации. Техника защиты информации. Требования к средствам высоконадежной биометрической аутентификации. М.: Стандартинформ, 2007. 16 с.
8. Постников Н. А. Анализ микроконтроллеров форм-факторов UICC/SIM и SD с функциями крипто-графической обработки информации // Информационные технологии в науке и образовании: проблемы и перспективы: материалы X Всерос. науч.-практ. конф. Пенза: ПГУ, 2023. С. 279–282.
9. ГОСТ Р ИСО/МЭК 19795-1-2007. Автоматическая идентификация. Идентификация биометрическая. Эксплуатационные испытания и протоколы испытаний в биометрии. Ч. 1. Принципы и структура. М.: Стандартинформ, 2009. 44 с.
10. ГОСТ Р 52633.3-2011. Защита информации. Техника защиты информации. Тестирование стойкости средств высоконадежной биометрической защиты к атакам подбора. М.: Стандартинформ, 2011. 24 с.
11. Иванов А. И., Иванов А. П., Горбунов К. А. Нейросетевое преобразование биометрии в код аутентификации: дополнение энтропии Хэмминга энтропией корреляционных связей между разрядами // Надежность и качество сложных систем. 2023. № 1 (41). С. 91–98. DOI:https://doi.org/10.21685/2307-4205-2023-1-11.
12. Иванов А. П., Постников Н. А. Методы вычисления энтропии выходных состояний нейросетевых преобразователей «биометрия-код» // Надежность и качество: тр. Междунар. симп. Пенза: ПГУ, 2024. Т. 1. С. 339–341.
13. Daugman J. Understanding Biometric Entropy and Iris Capacity: Avoiding Identity Crossover // Open Access Journal of AI and Machine Learning. 2024. URL: https://www.oajaiml.com/ (дата обращения: 13.07.2024).
14. Qt – Tools for Each Stage of Software Development Lifecycle. URL: https://www.qt.io / (дата обращения: 26.04.2025).
15. Boost C++ Libraries. URL: https://www.boost.org/ (дата обращения: 26.04.2025).
16. Постников Н. А. Численный эксперимент по вычислению энтропии выходных состояний нейросетевого преобразователя «биометрия – код» // Информационные технологии в науке и образовании. Проблемы и перспективы: материалы конф. Пенза: ПГУ, 2024. С. 313–316.
17. Постников Н. А., Иванов А. П. Оптимизация вычисления энтропии выходных состояний преобразователя «биометрия – код» с использованием полиномиальной аппроксимации // Вестн. Пенз. гос. ун-та. 2025. № 1 (49). С. 107–110.
18. Свидетельство о гос. регистрации программы для ЭВМ № 2024663986. Программа оценки энтропии через корреляционные связи выходных состояний кодов нейросетевого преобразователя биометрия-код / Иванов А. П., Постников Н. А.; заявл. 30.05.2024; опубл. 14.06.2024.
19. Свидетельство о гос. регистрации программы для ЭВМ № 2025664842 РФ. Программа синтеза таблицы связи между энтропией Шеннона и корреляционной сцепленностью разрядов выходной последовательности нейросетевого преобразователя биометрия – код / Иванов А. П., Постников Н. А.; № 2025666239: заявл. 16.06.2025; опубл. 24.06.2025.
20. Постников Н. А. Блочный метод оценки энтропии Шеннона бинарных последовательностей // Защита информации. Инсайд. 2025. № 3 (123). С. 72–77.
21. Свидетельство о гос. регистрации базы данных № 2025621577. База данных пересчета корреляционной сцепленности разрядов в энтропию выходных кодов нейросетевого преобразователя биометрия-код / Постников Н. А., Иванов А. П., Иванов А. И.; заявл. 24.04.2025; опубл. 14.05.2025.
22. NumPy Documentation. URL: https://numpy.org/ (дата обращения: 20.10.2024).















