Russian Federation
Russian Federation
Exploring deep-sea resources is an important step towards sustainable and efficient use of marine resources. Research may include analysis of biodiversity, ecosystem characteristics, and deep-sea fishing technologies and practices. Research in this area provides unique opportunities to advance understanding of the marine ecosystem for the development of deep-sea fisheries. This, in turn, helps to strengthen the sustainability and competitiveness of the Russian fishery complex in the long term. In the Russian Federation, the priority is to conduct scientific research in the field of deep-sea fishing, aimed both at developing the fishing of deep-sea objects and at studying them for the purpose of processing for the pharmaceutical industry. The development of innovative methods for catching mesopelagic fish and deep-sea aquatic organisms is an important task for the scientific community of the Russian Federation. The equations designed to describe various processes that occur during the operation of bottom and mid-depth trawl systems are discussed. The complexity of solving the above equations indicates the advisability of dividing exploitation processes into micro-level, macro-level and meta-level. The theory of multiphysics similarity allows you to simulate processes at various levels. Computer programs are presented that make it possible to recalculate the results of model experiments from a model of a trawl complex to a full-scale trawl complex.
equation, operation process, trawl complex, computer program
Введение
Для проведения экспериментальных испытаний и последующего пересчета результатов на модельный объект необходимо учитывать закономерности, которые были установлены теорией подобия. Это является важным аспектом в области промышленного рыболовства и судостроения [1]. Теория подобия заключается в методе научного обобщения результатов эксперимента. С применением данной теории появляется возможность проведения опытов на значительно меньших моделях, при этом исключается использование жестких физических явлений. В основе методов теории подобия лежат процессы масштабирования и моделирования процессов.
Теория подобия показывает, как следует проводить эксперименты и обрабатывать экспериментальные данные, а ограничившись минимальным числом опытов, можно обобщить результаты и получить закономерности изменения параметров для целых групп сходных явлений. Теории подобия позволяют изучать сложные процессы с достаточной для практики точностью, используя модели, которые значительно меньше их естественных размеров и зачастую проще. Они упрощают и удешевляют эксперименты.
В настоящее время теория подобия в области промышленного рыболовства является одной из самых больших научных дисциплин, которая занимается не только изучением вопросов сходства различных явлений и процессов, но и может с помощью анализа размерностей величин получать (с точностью до постоянной величины масштаба сходства) зависимости, которые характеризуют те или иные явления [2, 3]. Применительно к моделированию тралового комплекса возникают задачи выявления условий, обеспечивающих возможность пересчета результатов с модели на натуру, установления правил пересчета параметров, характеризующих механические, гидродинамические, грунтодинамические и другие про-
цессы тралового лова.
Применение теории подобия к траловым комплексам необходимо:
– для аналитического выявления зависимостей и связей, а также решения конкретных задач (например, составления графиков работы системы управления, боковых течений, штормов);
– работы с результатами экспериментальных исследований и испытаний тралового флота, когда результаты выражаются в обобщенных уравнениях;
– создания моделей траловых комплексов, воспроизводящих явления и процесс так же, как и полномасштабные траловые комплексы.
Данный подход позволяет углубленно исследовать различные аспекты работы траловых систем, от механики и гидродинамики до электродинамики и оптики, обеспечивая более полное понимание их работы и эффективности в различных условиях эксплуатации.
Цель и задачи исследования
Согласно принятой Правительством Российской Федерации Стратегии развития рыбохозяйственного комплекса Российской Федерации до 2030 г., исследования должны быть направлены на изучение глубоководных объектов добычи. Стратегия ориентирована как на совершенствование промысла глубоководных объектов, так и на их изучение с целью дальнейшей переработки в целях получения лекарственных препаратов. Разработка инновационных способов лова мезопелагических рыб и глубоководных гидробионтов – одна из главных задач, поставленная перед научным сообществом России.
Изучение глубоководных ресурсов является важным шагом в направлении устойчивого и рационального использования морских богатств. Исследования могут включать в себя анализ биологического многообразия, характеристик экосистем, а также технологий и методов промысловой деятельности в глубоководных условиях. Исследования в этой области предоставляют уникальные возможности для углубленного понимания морской экосистемы в рамках развития рыболовства в глубоководных районах. Это, в свою очередь, способствует укреплению устойчивости и конкурентоспособности рыбохозяйственного комплекса России в долгосрочной перспективе.
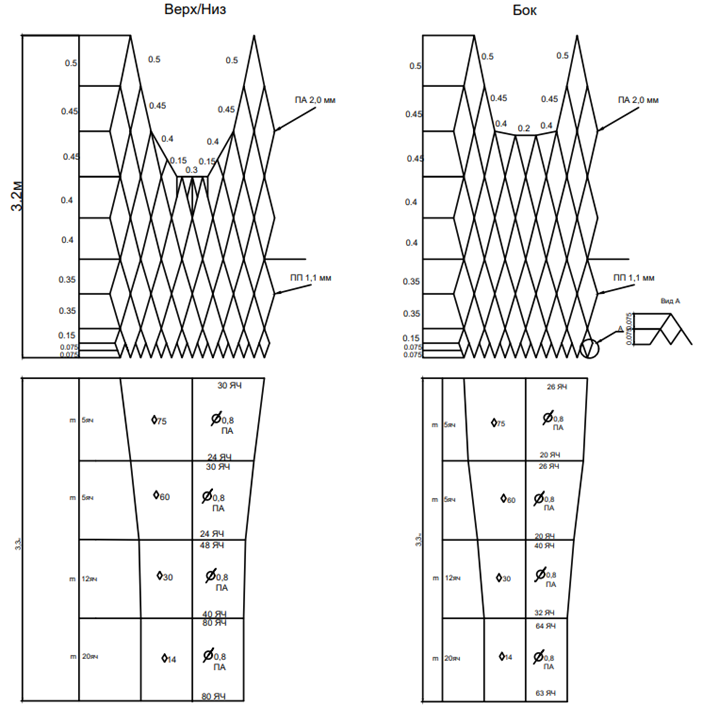
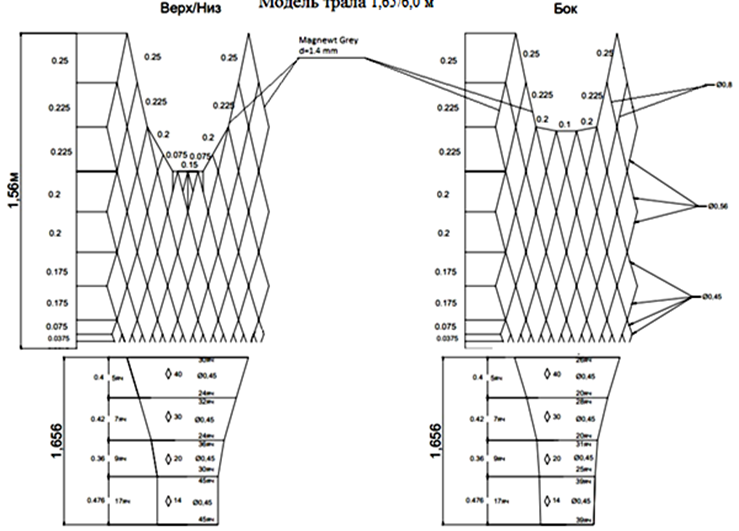
Цель настоящего научного исследования заключается в разработке правил планирования и проведения экспериментальных исследований моделей траловых комплексов на опытных установках (к примеру, гидроканал ОАО «МариНПО» – ООО «Фишеринг Сервис»), минимизации величины масштабного эффекта. На рис. 1, 2 представлены модели разноглубинного трала для лова ряпушки (Coregonus albula) в оз. Виштынецкое Калининградской области N-MWT-m1 3,3/12,0 м, N-MWT-m2 1,65/6,0 м и их чертежи, созданные на основе правил мультифизического подобия тралового комплекса [3] и компьютерной программы «Система автоматизированного проектирования орудий промышленного рыболовства» [4–6].

а
б
Рис. 1. Модель разноглубинного трала N-MWT-m1 3,3/12,0 м:
а – модель трала в потоке; б – чертеж модели трала
Fig. 1. Model of a multi-depth trawl N-MWT-m1 3.3/12.0 m:
a – model of a trawl in a stream; б – drawing of a trawl model

а
б
Рис. 2. Модель разноглубинного трала N-MWT-m2 1,65/6,0 м: а – модель трала в потоке; б – чертеж модели трала
Fig. 2. Model of a multi-depth trawl N-MWT-m2 1.65/6.0 m: a – model of a trawl in a stream; б – drawing of a trawl model
К задачам исследования относится вывод уравнений, описывающих процессы эксплуатации траловых комплексов (донного и разноглубинного).
Представленное в данной статье научное исследование направлено на композицию мультифизического моделирования различных по природе процессов, происходящих в системе «судно-трал» или траловом комплексе, в целях создания более точных, надежных и эффективных траловых систем, способных эффективно функционировать в разнообразных морских условиях и обеспечивать устойчивое и рациональное использование морских ресурсов.
Материалы и методы
Рассмотрим уравнения, описывающие процессы эксплуатации тралового комплекса. Запишем уравнения, определяющие механические движения тралового комплекса и его элементов, движение потока водных масс у тралового комплекса, грунтодинамический процесс движения элементов тралового комплекса (траловой доски и грунтропа донного трала), трение трала о поверхность слипа рыболовного судна и трение трала о поверхность тралового барабана и между канатно-сетными элементами трала, процесс электродинамики промысловых механизмов лебедок, температурное взаимодействие тралового комплекса и среды, освещенность процесса эксплуатации тралового комплекса и его видимость под водой, распространение звуковой волны от колебаний канатных элементов и др.
Рассмотрим уравнения, описывающие основные процессы, протекающие в траловых комплексах.
1. Уравнения механического движения тралового комплекса и его элементов (постановка и выборка трала). Используя уравнения движения системы трала, опускаемого или поднимаемого лебедкой, добавим крутящий момент к ротору двигателя траловой лебедки [7]:
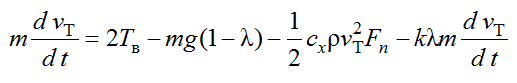 , (1)
, (1)
где m – масса траловой системы с уловом; vТ – скорость движения трала; t – время; Tв – сила натяжения в ваере; g – ускорение свободного падения; λ – отношение плотности воды к плотности траловой системы; cx – коэффициент гидродинамического сопротивления траловой системы; ρ – плотность воды; Fn – площадь канатно-сетной части трала с траловыми досками; k – коэффициент присоединенных масс.
2. Уравнения гидродинамики движения тралового комплекса и его элементов (постановка, траление и выборка трала). Независимо от формы трала поток воды описывается системой из двух уравнений: неразрывности и движения:
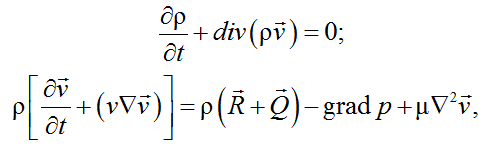 (2)
(2)
где v – модуль скорости потока воды относительно элементов тралового комплекса; – вектор скорости потока воды относительно элементов тралового комплекса;
– вектор гидродинамической силы сопротивления;
– вектор гидростатической силы; p – давление воды; m – динамическая вязкость воды.
3. Уравнения грунтодинамического движения тралового комплекса и его элементов (движение траловых досок и грунтропа донного трала):
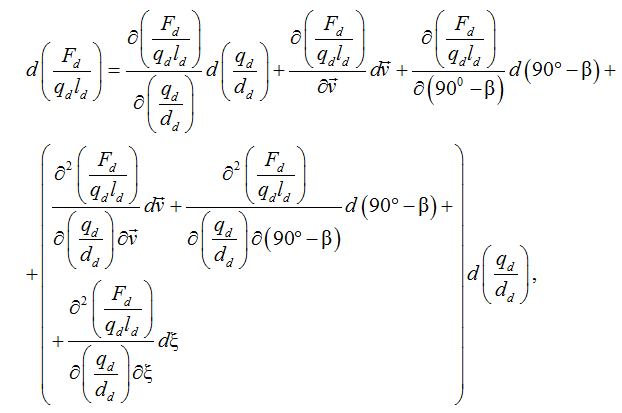 (3)
(3)
где Fd = Fxc – динамическая сила трения грунтропа; qd – вес одного метра грунтропа; ld – длина грунтропа; dd – диаметр бобинца грунтропа (катушек, каната); β – угол поворота грунтропа к вектору движения траловой системы; x – коэффициент укрута грунтропа (при условии, что грунтроп состоит их крученного каната).
4. Уравнения, характеризующие работу двигателя постоянного тока с независимым возбуждением (ДПТ НВ), описывают электромеханическую систему, управляемую регулируемым электрическим приводом.
Исходные уравнения динамики системы ДПТ НВ [7]:
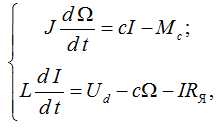 (4)
(4)
где J – момент инерции ротора; Ω – угловая скорость вращения ротора; c – коэффициент электродвижущей силы; I – сила тока; Mс – крутящий момент ротора; L – индуктивность; Ud – напряжение на якоре; RЯ – электрическое сопротивление цепи якоря.
Одновременно осуществляется рассмотрение трибологического процесса на барабане (промысловая схема имеет фрикционный барабан), на который набирается трал. Математическое описание динамики вращения барабана, движения траловой системы с уловом без проскальзывания и движения улова с проскальзыванием включает в себя дифференциальные уравнения соответственно:
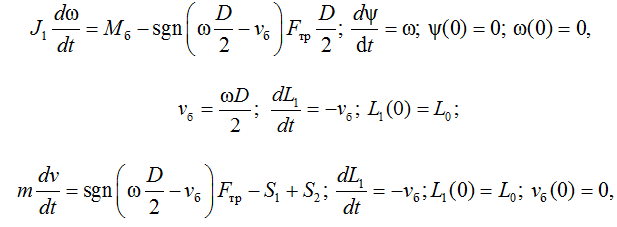 (5)
(5)
(6)
(7)
где J1 – момент (приведенный) инерции вала с барабаном и траловой системы; ω – угловая скорость вращения барабана; Mб – вращающий момент, приложенный к валу; D – диаметр барабана; vб – линейная скорость движения точки поверхности барабана; Fтр – сила трения фрикционного взаимодействия с поверхностью барабана; ψ – угол поворота вала; L1 – длина набегающей ветви траловой системы; L0 – длина набегающей ветви траловой системы в начале моделирования; S1 – натяжение в набегающей ветви траловой системы в точке касания барабана; S2 – натяжение в сбегающей ветви траловой системы в точке отрыва от барабана.
Таким образом, уравнения электромеханической системы и трибологического процесса представляют комплексный аппарат для анализа и моделирования рыболовных операций, обеспечивая более полное понимание физических взаимодействий в данной области.
Крутящий момент ротора двигателя Mс в электромеханической системе регулируемого электрического привода зависит от разнообразных факторов, таких как конструкция барабана, характеристики используемого двигателя, а также параметры системы управления. Данная зависимость отражает важные аспекты работы электромеханической системы, позволяя учесть вариации в крутящем моменте в зависимости от текущего состояния системы.
5. При решении задач управления траловым комплексом необходимо учитывать неоднородность водной среды с точки зрения термодинамики, ведь натурный трал работает в большом диапазоне глубин. К задачам термодинамики относятся и учет влияния гидроподпора внутри траловой системы, а именно в концевой его части и траловом мешке, и процесс адиабатного дросселирования воды, протекающей через сетную часть траловой системы (преграду).
Для решения данного рода задач добавим к системе уравнений (2) уравнение энергии:
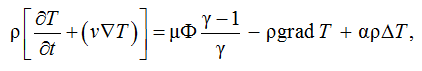 (8)
(8)
где T – температура воды; Ф – диссипативная функция, характеризующая работу внешних сил; γ – удельная теплоемкость; α – коэффициент температуропроводности.
6. Процесс распространения акустических волн в водной среде является адиабатным. Скорость распространения акустических волн описывается уравнением Лапласа, в котором дифференциал берется вдоль изоэнтропы:
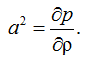 (9)
(9)
Неоднородное волновое уравнение акустики для траловой системы имеет вид
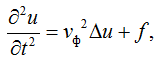 (10)
(10)
где u – функция, характеризующая профиль волны; vф – фазовая скорость звука в водной среде; f – функция внешних сил.
7. При управлении траловой системой используются как световые, так и радиоканалы связи. Мониторинг физических моделей трала и объекта лова возможен с применением систем пространственного видеонаблюдения, основанных в том числе на современных технологиях, например ToF [8]. Кроме указанных, в настоящее время актуальной задачей является исследование влияния различного рода бесконтактных воздействий, в том числе при помощи света, на поведенческие характеристики объекта лова. Для решения указанных задач необходимо учитывать законы распространения светового потока в неоднородных средах. Определяющее уравнение светового потока описывает зависимость величины светового потока от спектральной плотности:
 (11)
(11)
где Фv – световой поток; K(λ) – функция спектральной световой эффективности монохроматического излучения от длины волны λ; Фe,λ – спектральная плотность.
Для нормального человеческого глаза
![]() (12)
(12)
где Km – фотометрический эквивалент излучения, Km = 683 лм/Вт; V – относительная спектральная световая эффективность монохроматического излучения.
При применении для пространственной видеофиксации ToF-технологии (Time of Flight) при расчете расстояния до точки объекта наблюдения необходимо вносить поправку на зависимость фазовой скорости распространения света в неоднородных средах от показателя преломления
vс = C / n, (13)
а также учитывать явление дисперсии:
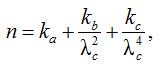 (14)
(14)
где vс – фазовая скорость света в среде с коэффициентом преломления n; C – скорость света в вакууме, C = 299 792 458 м/с; λc – длина световой волны в вакууме; ka, kb и kc – постоянные характеристики материала.
Зависимость (14) является эмпирической и была предложена О. Коши. Постоянные характеристики материала определяются для каждого материала опытным путем.
8. При моделировании работы траловой системы и ее управлении необходимо учитывать законы распространения акустических, световых и радиоволн
в неоднородной среде и влияние оптических систем на их распространение. Основные оптические законы (прямолинейного распространения, независимости, отражения, преломления) описываются уравнениями геометрической оптики. Уравнение преломления (закон Снеллиуса) описывает связь параметров преломления сред с углами падения и преломления луча:
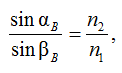 (15)
(15)
где αB – угол падения луча; βB – угол преломления луча; n1 и n2 – абсолютное преломление первой и второй среды.
Рассмотрим оптическую систему на примере сферической линзы: расстояние связывается с оптической силой линзы, ее геометрией и показателями
преломления сред и имеет следующую зависимость:
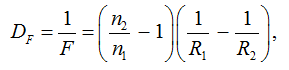 (16)
(16)
где DF – оптическая сила; F – фокусное расстояние; R1 и R2 – радиусы кривизны сферических поверхностей линзы.
Приведенные уравнения, описывающие процессы эксплуатации траловых комплексов, позволяют привести их в критериальные уравнения мультифизического подобия тралового комплекса, что позволит обосновать критерии подобия и автомодельность выполнения соответствующих критериев подобия.
Допустим, что условия геометрического, статического, кинематического и динамического подобия выполнены. В этом случае во всех сходственных точках выдерживаются постоянными масштабы однородных физических величин [9]. Чтобы перейти от натуры к модели тралового комплекса, надо все физические величины, входящие в уравнения (1)–(16), выразить с помощью масштабов подобия через соответствующие параметры модели тралового комплекса.
В этой связи требуется разработка специализированных компьютерных программ, способных обрабатывать и анализировать обширные объемы данных в мультифизическом контексте рыболовства. Для достижения этой цели нам потребуется команда специалистов, включающая разработчиков программного обеспечения, инженеров по рыболовству, физиков, математиков и других экспертов. Нам может потребоваться создание специализированных алгоритмов для численного расчета масштабов и критериев подобия в различных физических аспектах рыболовства. Эти алгоритмы могут включать в себя моделирование гидродинамических процессов, теплопередачи, световых и звуковых волн, электромагнитных полей и других физических явлений, характерных для рыболовства. Для визуализации результатов работы в трехмерном формате понадобится специализированное программное обеспечение для визуализации данных, которое позволит наглядно представить сложные физические взаимодействия, происходящие в процессах рыболовства.
Иллюстрации снимков экрана рабочего стола программ «Масштабы мультифизического подобия процессов рыболовства» и «Критерии мультифизического подобия процессов рыболовства», представленные на рис. 3, 4, демонстрируют не только функциональность программ, но и их пользовательский интерфейс, что обеспечивает удобство использования для научных исследователей и специалистов в области рыболовства.
Рис. 3. Рабочий стол компьютерной программы
«Масштабы мультифизического подобия процессов рыболовства»
Fig. 3. Desktop of the computer program
“Scales of multiphysical similarity of fishing processes”
Рис. 4. Рабочий стол компьютерной программы
«Критерии мультифизического подобия процессов рыболовства»
Fig. 4. Desktop of the computer program
“Criteria of multiphysical similarity of fishing processes”
Результаты
На рис. 5 представлены графики зависимостей Rx = f(v) для двух моделей тралов: N-MWT-m1 3,3/12,0 м и N-MWT-m2 1,65/6,0 м.
Также на этом рисунке представлены кривые Cr = f(Cl), обозначенные как Am11Am12 и Am21Am22, которые представляют собой зависимости мультифизического подобия тралов (множество кривых).
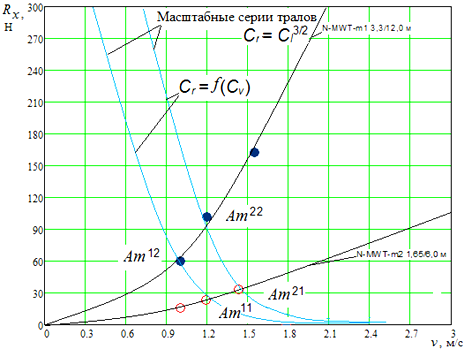
Рис. 5. Графики зависимостей Cr = f(Cv) и Rx = f(v)
Fig. 5. Dependency graphs Cr = f(Cv) and Rx = f(v)
Отклонение от кривых Am11Am21 и Am12Am22 означает нарушение подобия при условии соблюдения масштабов. Кривая Am11Am21 отражает зависимость Rx = f(v) для модели трала N-MWT-m2 размером 1,65/6,0 м, а кривая Am12Am22 представляет собой зависимость Rx = f(v) для модели трала N-MWT-m1 размером 3,3/12,0 м.
Эти графики позволяют визуально оценить соотношения между силой сопротивления трала Rx, скоростью v и коэффициентом мультифизического подобия Cr, Cl для различных моделей тралов. Анализ отклонений от кривых мультифизического подобия дает понимание, насколько эффективно поддерживается подобие в условиях изменения параметров трала.
Аппроксимация соответствующих зависимостей Rx = f(v) в критериальном виде Ne = f(Re) предоставляет возможность тщательно обосновать автомодельность гидродинамического коэффициента сопротивления траловой оболочки cx в зависимости от числа Рейнольдса Re, играющего ключевую роль в гидродинамике, характеризуя отношение между инерционными и вязкостными характеристиками потока. Таким образом, аппроксимация зависимостей Rx = f(v) в критериальной форме предоставляет основание для выявления закономерностей, связывающих нагрузку трала, скорость потока с числом Рейнольдса, что позволяет выделить характерные взаимосвязи между параметрами траловой системы.
Обоснование автомодельности гидродинамического коэффициента сопротивления траловой оболочки в зависимости от числа Рейнольдса через аппроксимацию существенно улучшает понимание физических процессов, происходящих в траловой системе, предоставляет более обобщенный и устойчивый метод описания воздействия различных факторов на сопротивление трала в различных условиях промысла.
Заключение
В представленной научной статье авторами рассмотрены уравнения, описывающие процессы эксплуатации траловых комплексов (донного и разноглубинного). Определяются необходимые условия, обеспечивающие возможность пересчета результатов, полученных при моделировании тралового комплекса, на реальные натурные траловые комплексы. В рамках исследования определены правила пересчета параметров, характеризующих различные процессы, протекающие в траловых комплексах.
Для систематизации, анализа и синтеза большого объема данных, полученных в ходе экспериментов, используются специально разработанные компьютерные программы. Для верификации полученных данных предложено проводить эксперименты с использованием мультифизического подобия процессов тралового промысла.
1. Sedov L. I. Metody podobiya i razmernosti v mekhanike [Similarity and dimensionality methods in mechanics]. Moscow, Nauka Publ., 1977. 440 p.
2. Nedostup A. A. Fizicheskoe modelirovanie gidro-dinamicheskih processov dvizheniya orudij rybolovstva [Physical modeling of hydrodynamic processes of fishing gear movement]. Vestnik Tomskogo gosudarstvennogo universiteta. Matematika i mekhanika, 2012, no. 3 (19), pp. 55-67.
3. Nedostup A. A., Razhev A. O. Sozdanie pravil mul'tifizicheskogo podobiya tralovogo kompleksa [Creation of rules for the multiphysical similarity of the trawl complex]. Morskie intellektual'nye tekhnologii, 2021, no. 1, vol. 1, pp. 132-137.
4. Razhev A. O., Nedostup A. A., L'vova E. E. Arhitektura programmnogo obespecheniya sistemy avtomatizirovannogo proektirovaniya orudij promyshlennogo rybolovstva [Software architecture of the computer-aided de-sign system for industrial fishing tools]. Materialy 64-j Mezhdunarodnoj nauchnoj konferencii Astrahanskogo gosudarstvennogo tekhnicheskogo universiteta, posvyashchennoj 90-letnemu yubileyu so dnya obrazovaniya Astrahanskogo gosudarstvennogo tekhnicheskogo universiteta (Astrahan', 2020): Astrahan', Izd-vo AGTU, 2020. Rezhim dostupa: 1 CD-disk. № gos. registracii 0322002778. Available at: http://www.astu.org/Uploads/files/izdatelstvo/64-%D1%8F%20%D0%BA%D0%BE%D0%BD%D1%84%D0%B5%D1%80%D0%B5%D0%BD%D1%86%D0%B8%D1%8F_%D0%A71.zip (accessed: 06.12.2021).
5. Razhev A. O., Nedostup A. A., L'vova E. E. Raschet formy i nagruzok v rybolovnom trale v processe ego pro-ektirovaniya [Calculation of the shape and loads in a fishing trawl during its design]. Materialy 64-j Mezhdunarodnoj nauchnoj konferencii Astrahanskogo gosudarstvennogo tekhnicheskogo universiteta, posvyashchennoj 90-letnemu yubileyu so dnya obrazovaniya Astrahanskogo gosudarstvennogo tekhnicheskogo universiteta (Astrahan', 2020): Astrahan', Izd-vo AGTU, 2020. Rezhim dostupa: 1 CD-disk. № gos. registracii 0322002778. Available at: http://www.astu.org/Uploads/files/izdatelstvo/64-%D1%8F%20%D0%BA%D0%BE%D0%BD%D1%84%D0%B5%D1%80%D0%B5%D0%BD%D1%86%D0%B8%D1%8F_%D0%A71.zip (accessed: 06.12.2021).
6. Razhev A. O., Nedostup A. A., L'vova E. E. Ma-tematicheskaya model' vizualizacii kruchenyh kanatno-verevochnyh izdelij dlya zadach proektirovaniya orudij promyshlennogo rybolovstva [A mathematical model for visualization of twisted rope products for the tasks of designing tools for industrial fishing]. Prirodnye resursy, ih sovremennoe sostoyanie, ohrana, promyslovoe i tekhnicheskoe ispol'zovanie: materialy XI Nacional'noj (Vserossijskoj) nauchno-prakticheskoj konferencii (Petropavlovsk-Kamchatskij, 24–25 marta 2020 g.). Petropavlovsk-Kamchatskij, Izd-vo KamchatGTU, 2020. Pp. 222-226.
7. Nedostup A. A., Naumov V. A., Razhev A. O., Dy-atchenko S. V. Uravneniya elektrodinamicheskogo podobiya tralovyh lebedok s elektricheskim privodom [Equations of electrodynamic similarity of electric powered trawl winches]. Morskie intellektual'nye tekhnologii, 2020, no. 4, vol. 1, pp. 87-91.
8. Soloshchev O. N., Slyusar V. I., Tverdohlebov V. V. Fazovyj metod izmereniya dal'nosti na osnove teorii mnogokanal'nogo analiza [A phase-based range measurement method based on the theory of multichannel analysis]. Artillerijskoe i strelkovoe vooruzhenie, 2007, no. 2 (23), pp. 29-32.
9. Nedostup A. A., Razhev A. O. Matematicheskoe modelirovanie orudij i processov rybolovstva. Chast' II: monografiya [Mathematical modeling of fishing tools and processes. Part II: monograph]. Kaliningrad, Izd-vo KGTU, 2014. 249 p.
















