Russian Federation
Russian Federation
Russian Federation
A method is proposed to solve the problems that arise when analyzing information obtained from various sources, it is necessary to combine it in a complex of coordinated stochastic models. For most processes of mechanical destruction of machine parts, such as wear, fatigue volumetric or surface destruction, corrosion, etc., the monotony of the implementation of degradation processes leading to failures is characteristic. The scheme of resource allocation formation is given, which corresponds to the main types of mechanical failures occurring in the elements of ship mechanisms. The diagram illustrates a fairly general case when, with an increase in the operating time of an element, its resistance to destruction decreases monotonously, and the damage parameter also increases monotonously. Based on the use of generalized distributions, it is possible to obtain several variants of complexes of mechanical reliability models in which the resource allocation has a fairly simple analytical form. When modeling degradation processes, the DM distribution can be obtained as a special case of distributions and without using the Markov model of random processes. Only the mixing condition of the process implementations is essential. Obtaining various types of operating time distributions before the parameter reaches a fixed level using the obtained dependencies is not associated with any assumptions about the nature of individual implementations of the degradation process, except for their monotony. From the point of view of practical application, the distribution under consideration, obtained on the basis of Weibull’s law, has the advantage of universality, since, unlike the normal law, it can also be used for values of the coefficient of variation significantly exceeding 0.3.
reliability, stochastic models, processes of destruction of parts, gamma-percent operating time, final state, distribution of operating time to failure
Introduction
Experimental studies of the mechanical reliability of ship technical equipment may include the following components:
– tests (most often bench tests) conducted for the purpose of statistically assessing the characteristics of resistance of elements to mechanical failure (fatigue, static, wear, etc.);
– measurements of the operational load of elements for the purpose of statistically assessing the characteristics of loading that determine the process of damage accumulation;
– measurements of the parameters of the technical condition (damage) of elements for the purpose of statistically assessing the characteristics of degradation processes leading to parametric failures;
– operational tests or observations conducted for the purpose of statistically assessing the characteristics of the operational life of elements [1-3].
Purpose of the research. One of the problems that arise when analyzing information obtained from the listed sources is to combine it in a complex of mutually agreed stochastic models. The presence of such complexes for various machine elements allows them to be used in the future to solve various problems of forecasting and ensuring mechanical reliability.
Materials and methods of the study
Let us consider the general principles of construction and methods of statistical evaluation of the parameters of mechanical reliability model complexes. The logical foundations for constructing such a complex in the case of scalar parameters of damageability and resistance to destruction during gradual (degradation) failures can be obtained from consideration of the scheme for forming the distribution of the element’s resource (Figure). According to this scheme, a mechanical failure occurs at the moment of intersection of a random realization of the damageability parameter xd(t) of an element with a random realization of its resistance parameter xr(t). With monotonic realizations of random processes xd(t) and xr(t), only their single intersection is possible in the region abcd, where the resource distribution is formed.
Most processes of mechanical destruction of machine parts, such as wear, fatigue volumetric or surface destruction, corrosion, etc., are characterized by monotony of the implementation of degradation processes leading to failures. Therefore, the scheme of formation of resource distribution, shown in the figure, corresponds to the main types of mechanical failures occurring in elements of ship mechanisms.
The diagram illustrates a fairly general case when, with increasing service life of an element, its resistance to destruction decreases monotonically, and the damage parameter also increases monotonically. A typical example of such a process of failure formation can be the accumulation of fatigue damage and destruction of threaded connections with a gradual weakening of their preliminary tightening. A decrease in the preliminary tightening force, caused by the process of micro-crushing of the surfaces of joints and threads, leads to an increase in the variable component of the load acting on the bolts of the connection [2], that is to an increase in the damage parameter xd, which can be the value of the equivalent stress amplitude in the bolt. The resistance parameter xr in this case is the limit of limited endurance of the bolt, the realizations of which, forming a family of individual fatigue curves, monotonically decrease with increasing service life. When the increasing realization reaches the equivalent amplitude of the individual fatigue curve, a failure occurs.
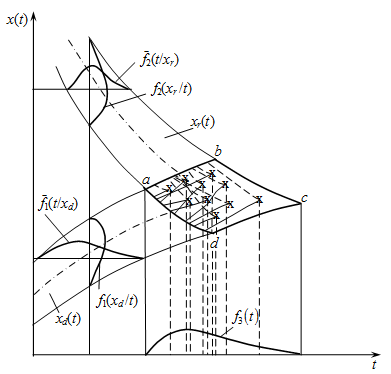
Diagram of different reliability models
Random processes of change of parameters of resistance xr(t) and damageability xd(t) of elements are non-stationary, however, the condition of monotonicity of realizations allows to use only one-dimensional distributions with characteristics depending on service life when solving reliability problems, which simplifies the mathematical apparatus and makes it possible to obtain analytical results for many practically important cases.
From the conditions of monotonicity of realizations of processes xd(t) and xr(t) follow relations connecting their one-dimensional distribution densities at fixed values of service life f1(xd / t) and f2(xr / t) with the distribution densities of service life at fixed values of damageability and resistance to destruction parameters f̄1(t / xd) and f̄2(t / xr):
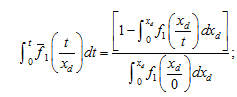
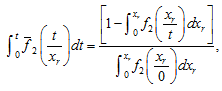(1)
here f1(xd / 0) and f2(xr / 0) – are the distribution densities of the initial (at t = 0) values of the damageability and fracture resistance parameters, respectively.
If there is no initial dispersion of the damageability and fracture resistance parameter values, then in (1) one should take 
.
When constructing complexes of models of mechanical degradation failures for describing random monotonic degradation processes, it is possible to use two classes of generalized basic distributions of functions of random arguments. The first such class of basic generalized normal distributions has a density of the form
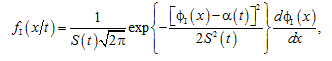(2)
here ϕΙ(x) – is a deterministic monotonically increasing from –∞ to +∞ function of a random variable x in the range of its variation; α(t) – is a deterministic parametric function of the operating time, describing a monotonous degradation process on average; S(t) – is a deterministic parametric function of the operating time, used to describe the pattern of change in the degree of dispersion of the degradation process.
The second class of generalized basic laws is gamma distributions, the density of which is described by the expression
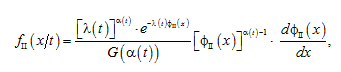(3)
here ϕΙΙ(x) – is a deterministic positive function of the random variable x that increases monotonically from zero; l(t) – is a deterministic parametric function of the operating time that describes the monotonic process on average; a(t) – is a deterministic parametric function of the operating time that characterizes the change in the degree of dispersion of the degradation process.
Based on the use of generalized distributions (1) and (2), it is possible to obtain several variants of reliability model complexes in which the resource distribution has a fairly simple analytical form.
Results of the study and their discussion
In the class of generalized normal distributions (1), when ϕΙ(x) = x, we have a standard normal law with a mean value α(t) and standard deviation S(t) monotonically changing depending on the operating time. When ϕΙ(x) = lnx, we obtain a logarithmically normal distribution, and if we set ϕΙ(x) = x3, then the resulting distribution is a generalized normal law. In the case of a monotonically increasing process with a one-dimensional normal law, the distribution density of the damage parameter for a fixed operating time has the form
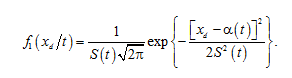(4)
Then, in the absence of initial dispersion of the damage parameter, from expression (1), in which – was taken as the lower limit of integration over xd, it follows that the distribution density of the operating time at a fixed value of the damage parameter is determined by the expression
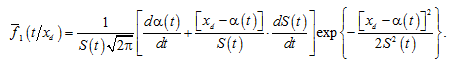(5)
In the list of works [4-6] when describing degradation processes, a “fan” model is used, for which it is possible to take α(t) = m0 + tν / μ and S(t) = σ0tν / μ at n > 0. In this case, the coefficient of variation of the process хd(t) at m0 ≠ 0 increases with increasing operating time, but is limited from above by the value σ0, and at m0 = 0 it is equal to σ0. Then from (4) we have a normal distribution of the damage parameter with a density
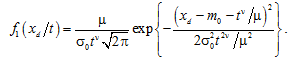
Using (5), we obtain the distribution density of the operating time until the parameter reaches a fixed level
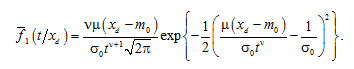(6)
The corresponding distribution function of operating time is expressed using the normalized distribution function:
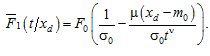
The gamma percentage operating time before the parameter reaches the limit value хl is determined in this case by the formula
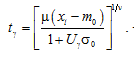(7)
In the linear version, when n = 1, expression (6) is the density of the well-known alpha distribution, which has been widely used in solving various parametric reliability problems. The average operating time to the limit value хd = хl in the case of alpha distribution when s0 £ 0.25 is approximately determined by the formula T ≈ μ(хl – m0)(1 + σ02 ).
With the same parametric function for the average α(t) = m0 + tν / μ, one can set the function S(t), which determines the dispersion of the parameter хd in the form characteristic [3] for processes with “mixing” of realizations 
, i. e. when the process хd(t) has a variation coefficient at t = (μm0)1/ν with a maximum equal to 
, and then decreases with increasing operating time. Then from (4) we obtain an expression for the density of the normal distribution of the damage parameter
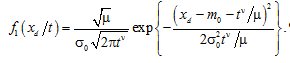
For a fixed value of the parameter хd, the corresponding expression for the distribution density of the operating time follows from (5):
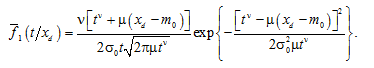(8)
Considering that the distribution function of the operating time before the parameter reaches a fixed level хd has the form
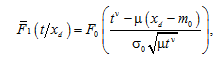(9)
the median operating time until the parameter reaches the limit value хl is determined by the formula
t0.5 = [μ(хl – m0)]1/ν.
From (9) follows also the general expression for the gamma-percentage operating time before the parameter reaches the limit value
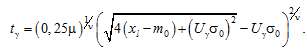
In the particular case of a linear dependence of the average α(t) on the operating time at n = 1, expression (7) represents the distribution density. The density of this distribution can be transformed to the form
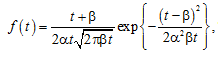
here 
The average operating time until the damage parameter reaches the limit value хl in this case is determined by the formula
and the coefficient of variation of the operating time is expressed as
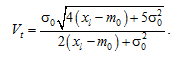
In works of this type, the distribution [7-10], obtained on the basis of considering degradation processes as diffusion Markov and used in constructing “probabilistic-physical” reliability models, is called diffusion monotone (DM-distribution). From the above it follows that when modeling degradation processes, the DM-distribution can be obtained as a special case of distributions and without using the Markov model of random processes. The only essential condition is the mixing of process realizations. It should be noted that obtaining different types of distributions of operating time before the parameter reaches a fixed level using (3) is not associated with any assumptions about the nature of individual realizations of the degradation process, except for their monotony.
The determination of the mean value and the variation coefficient of the generalized DM-distribution of the form (8) for ν ≠ 1 can be performed numerically. For this purpose, it is convenient to first move from (8) to the distribution of the dimensionless quantity τ = t / t0.5, the density of which depends only on two parameters ν and α:
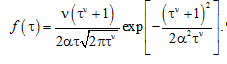
Having calculated the integral 
, the average value of the operating time until the parameter хd(t) reaches the limit value хl is then determined by the formula:
The coefficient of variation is determined using the expression
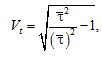
in which the value of the initial moment of the second order is also obtained using numerical integration:
Based on the basic generalized gamma distribution (3), a type of distribution convenient for practical use in describing degradation processes can be obtained if we set α(t) ≡ 1; ϕΙΙ(x) = xb; and 
. Then the distribution of the damage parameter for a fixed operating time will similarly be the Weibull law with a density
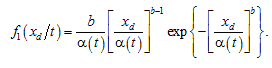
In this case, the distribution density of the operating time until the monotonically increasing damage parameter reaches a fixed value, based on (1), is obtained in the form:
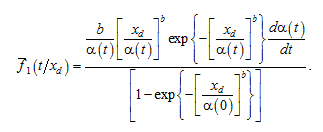(10)
Putting into (10) a parametric function that determines the behavior of the degradation process on average in the form α(t) = α0 + tν / μ, we obtain
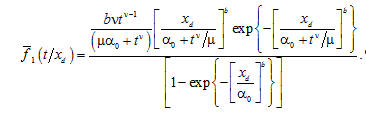
The gamma percentage operating time before the parameter reaches the limit value хl is determined by the formula
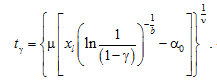(11)
In the case of α0 = 0, expression (11) is the density of V. N. Treyer’s distribution.
For “fan” models of degradation processes, the constancy of the coefficient of variation of the value хd is characteristic with a change in the operating time. This condition corresponds to the normal distribution of the damage parameter (11) with α(t) = tν / μ and S(t) = s0tν / μ and the Weibull distribution with α(t) = α0 + tν / μ and b = const.
If we set α0 = 0, then we can calculate the value χγ = tγ / t0.5, for these distributions, i.e. the coefficient that allows us to move from the median operating time t0.5 to the gamma-percent operating time using the formula tγ = χγt0.5. Some results of such a calculation for γ > 0.8 are given in the table for three values of the exponent ν = 2/3, 1 and 3/2 and two values of the coefficient of variation of the damage parameter: 0.2 (above the line) and 0.3 (below the line).
Using the data in the Table, we can compare the nature of the dispersion of the operating time until the parameter reaches its limit value when using the normal distribution and the Weibull law for the density f1(xd / t). If 0.8 ≤ γ ≤ 0.95, and the variation coefficient хd is 0.3, then the difference in the value of the transition coefficient χγ between these laws is practically absent.
With a variation coefficient of 0.2, it is very insignificant and becomes noticeable only when γ > 0.95.
The value of the coefficient of transition from the median resource to the gamma-percentage
with an increasing degradation process
|
Distribution type |
ν |
g |
|||||
|
0.8 |
0.9 |
0.95 |
0.99 |
0.999 |
0.9999 |
||
|
Normal |
2/3 |
0.7918 0.7134 |
0.7100 0.6137 |
0.6526 0.5479 |
0.5638 0.4520 |
0.4858 0.3738 |
0.4343 0.3250 |
|
1 |
0.8559 0.7984 |
0.7959 0.7222 |
0.7524 0.6696 |
0.6825 0.5890 |
0.6180 0.5189 |
0.5735 0.4727 |
|
|
3/2 |
0.9015 0.8606 |
0.8588 0.8050 |
0.8272 0.7654 |
0.7752 0.7027 |
0.7255 0.6457 |
0.6903 0.6068 |
|
|
Weibull |
2/3 |
0.8042 0.7133 |
0.7331 0.6177 |
0.6849 0.5558 |
0.6127 0.4678 |
0.5517 0.3975 |
0.5122 0.3542 |
|
1 |
0.8648 0.7983 |
0.8130 0.7253 |
0.7770 0.6760 |
0.7214 0.6026 |
0.6727 0.5406 |
0.6402 0.5006 |
|
|
3/2 |
0.9077 0.8606 |
0.8711 0.8073 |
0.8452 0.7702 |
0.8044 0.7134 |
0.7677 0.6636 |
0.7428 0.6305 |
|
The data in the table also indicate that the distributions of the operating time have a sufficiently large lower “threshold” level, ensuring a service life reserve with a high probability of failure-free operation g = 0.9999, which is from 32.5 to 74.3% of the median operating time. From the point of view of practical application, the distribution of type (11) based on the Weibull law has the advantage of universality, since, unlike the normal law, it can also be used with values of the coefficient of variation of the quantity хd that significantly exceed 0.3.
Conclusions
Statistical control of mechanical reliability of resource-providing elements of machines can be reduced to standard selective quality control by an alternative feature. The possibilities of parametric control of mechanical reliability are shown, the use of which allows replacing expensive control tests with current control of technological parameters that determine the resource of the object. Using the data in the Table, we can compare the nature of the dispersion of the operating time until the parameter reaches its limit value when using the normal distribution and the Weibull law for the density.
1. Te A. M. Ekspluatatsiia sudovykh vspomogatel'nykh mekhanizmov, sistem i ustroistv [Operation of ship's auxiliary mechanisms, systems and devices]. Vladivostok, Izd-vo MGU imeni admirala G. I. Nevel'skogo, 2014. 177 p.
2. Bashurov B. P., Skiba A. N., Chebanov V. S. Funktsional'naia nadezhnost' i kontrol' tekhnicheskogo sostoianiia sudovykh vspomogatel'nykh mekhanizmov: ucheb-noe posobie [Functional reliability and control of the technical condition of ship's auxiliary mechanisms: a textbook]. Novorossiisk, Izd-vo MGA imeni admirala F. F. Ushakova, 2009. 192 p.
3. Pavlov I. V. Statisticheskie metody otsenki nadezhnosti slozhnykh sistem po rezul'tatam ispytanii [Statistical methods for evaluating the reliability of complex systems based on test results]. Moscow, Radio i sviaz' Publ., 1992. 168 p.
4. Miasnikov Iu. N. Osnovy teorii nadezhnosti i diagnos-ticcheskogo obespecheniia sudovykh energeticheskikh ustanovok: uchebnoe posobie [Fundamentals of the theory of reliability and diagnostic support of marine power plants: textbook]. Saint Petersburg, Izd-vo SPGUVK, 2010. 183 p.
5. Polovko A. M., Gurov S. V. Osnovy teorii nadezhnosti [Fundamentals of reliability theory]. Saint Petersburg, BKhV-Peterburg Publ., 2006. 704 p.
6. Nadezhnost' i effektivnost' v tekhnike: spravochnik: v 10 tomakh. Vol. 5. Proektnyi analiz nadezhnosti [Reliability and efficiency in engineering: handbook: in 10 volumes. Vol. 5. Design reliability analysis]. Pod redaktsiei V. I. Patrusheva i A. I. Rembezy. Moscow, Mashinostroenie Publ., 1988. 316 p.
7. Venttsel' E. S., Ovcharov L. A. Teoriia veroiatnostei i ee inzhenernye prilozheniia [Probability theory and its engineering applications]. Moscow, Nauka Publ., 1988. 480 p.
8. Golovchenko V. P. Vozmozhnosti ispol'zovaniia raspredeleniia Veibulla v kachestve universal'noi modeli ap-proksimatsii [Possibilities of using the Weibull distribution as a universal approximation model]. Trudy Gosudar-stvennogo nauchno-issledovatel'skogo instituta grazhdanskoi aviatsii, 1988, no. 279, pp. 91-98.
9. Kapoor K., Lamberson L. Reliability in engineering design. John Wiley, 1977. 586 p. (Kapur K., Lamberson L. Nadezhnost' i proektirovanie sistem / per. s angl. E. G. Kova-lenko. M.: Mir, 1980. 604 s.).
10. Collins J. Failure of Materials in Mechanical Design. John Wiley & Sons, 1981. 654 p. (Kollinz Dzh. Povrezhdenie materialov v konstruktsiiakh / per. s angl. A. M. Vasil'eva. M.: Mir, 1984. 624 s.).
